1531834467

<19.

> Techniki algorytmiczne - przybliżone i dokładne

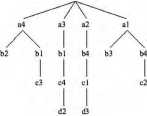
Rysunek 8.

Drzewo ilustrujące przebieg algorytmu poszukiwań z nawrotami, służącego do znalezienia wszystkich ustawień czterech nieatakujących się hetmanów na szachownicy o wymiarach 4x4

Ćwiczenie 25. Narysuj szachownicę 5x5 i posługując się opisanym algorytmem rozstawiania hetmanów znajdź na niej wszystkie ustawienia pięciu nieatakujących się hetmanów.

Ćwiczenie 26. Weź prawdziwą szachownicę i spróbuj ustawić na niej 8 nieatakujących się hetmanów. Po otrzymaniu pierwszego ustawienia, wykonaj dalsze kroki algorytmu, by otrzymać kilka następnych ustawień.

Opis poszukiwania z nawrotami w języku Pascal

Zaprogramowanie poszukiwania z nawrotami nie jest specjalnie trudne. Najpierw musimy rozstrzygnąć dwie kwestie: w jaki sposób reprezentować ustawienie hetmanów na planszy i jak sprawdzać, czy dwa hetmany nie atakują się.

1.    Ponieważ w każdej kolumnie może się znaleźć co najwyżej jeden hetman, ustawienie nieatakujących się hetmanów można opisać, podając dla każdej kolumny jedynie numer wiersza, w którym stoi hetman znajdujący się w tej kolumnie. Niech h [l.. n] będzie tablicą, w której h [i] jest numerem wiersza zawierającego hetmana, stojącego w kolumnie i. Ustawienie z rys. 7d można opisać jako (3,1,4,2).

2.    Ustawiając kolejnego hetmana musimy sprawdzić, czy jego pozycja nie jest atakowana przez żadnego innego hetmana, ustawionego we wcześniejszych kolumnach. Przypuśćmy, że chcemy ustawić hetmana w kolumnie i w wierszu h[i]. Najpierw musimy sprawdzić, że żaden hetman w poprzednich kolumnach nie stoi w tym samym wierszu, czyli ma być h[l] ? h[i] dla każdego 1 spełniającego 1 < i. Ponadto, aby dwa hetmany nie atakowały się po przekątnych, musi być spełniony warunek |h[l] - h[i]| # |l - i| dla

Ćwiczenie 27. Uzasadnij, że rzeczywiście spełnienie warunku wymienionego w punkcie 2 powyżej gwarantuje, że żadne dwa hetmany nie atakują się po przekątnych. Sprawdź najpierw na przykładzie szachownicy 4x4.

Przedstawiamy poniżej funkcję w języku Pascal o nagłówku:

function Hetmany(n:integer):integer;

ę hetmanów na szachownicy nxn. Tekst tej eznaczenia poszczególnych instrukcji i efek-astępnego wiersza w kolumnie i, w którym hetmana z poprzednich kolumn.

której wartością jest liczba różnych rozstawień nieataku funkcji zawiera wiele komentarzy, ułatwiających zrozum tów ich działania. Wyjaśnijmy jedynie, że x[i] oznacza można ustawić hetmana nie atakowanego przez żadneg

%SSSSSSL |J££    =S[0]