1588093939

123456789101112131415

Zo-K -

Zauważmy, że graf G (rys.3) jest niespójny, węzły identyfikowane nr. 11, 12 nie są powiązane z żadną krawędzią. Nazywa się je węzłami swobodnymi. Widać to także w zapisach macierzowych w S_w i Z_W._K. Wyróżniając elementy powiązane w grafie G można określić podgraf spójny G’ w G [10, 11]:

G cG,    (2)

G uw_nuw_l2 = G.    (3)

3. Konwersja wyjściowych danych do nowych form

Przedstawiony graf G (rys.2) oraz jego zapisy macierzowe S_w, Zw-k * Zo-k- wykorzystam do tworzenia nowych struktur zapisu topologii danych przestrzennych.

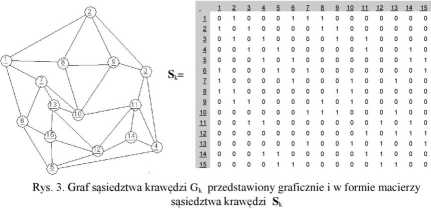
Zauważmy, że w oparciu o macierz Zw-k można określić graf sąsiedztwa krawędzi G_k, przedstawiony na rys.3. Można go zapisać za pomocą macierzy S_K.

Można zauważyć, że:

S_K.= (Z_W-k )^T( Z_W-k) - D₂    (4)

gdzie Di jest macierzą diagonalną o wartościach równych 2. Element macierzy (s_k)ij (i, j £ [I, 2,..., 151) przyjmuje wartość równą 1, jeśli krawędź i przylega do krawędzi j w grafie G (krawędzie i, j dochodzą do wspólnego węzła).

Macierz Z₀-k zawiera dane, które pozwalają na wygenerowanie informacji o sąsiedztwie obszarów. Na rys.4 przedstawiono to sąsiedztwo w formie grafu G₀ i zapisu macierzowego S₀. Macierz S₀ otrzymuje się poprzez działanie:

So= (Zo-k) (Zo-k)^T- Do    (5)

gdzie D₀ jest macierzą diagonalną o wartościach d_u równych liczbie krawędzi opisujących obszar i.

4