226618610

PRZEGLĄD TECHNICZNY.

Znaleziony wzór poucza, że fJ_s rośnie od wartości 0, gdy sita Pj>rzesuwa się od przegubu A ku górze i osiąga nych

l-/^/ł*+ *' + J^ • • '

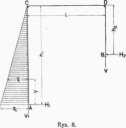
a więc powyżej narożnika C. Praktycznie największe H, i najmniejsze //, powstanie zatem, gdy sita P działa w na- //_T^ ,

Działanie sil poziomych, jednostajnie rozloio-slup ramy równoramiennej. Kładąc po prawoj stronie wzoru (IV) P = gdy = qldt\ i całkując w granicach od i) = 0 do ą = znajdujemy //, podobnie jak V w § 6.

Po zcałkowaniu i uproszczeniu wypada:

112

Pił*

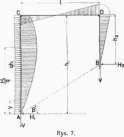
§ &. Działanie sil poziomych, rozłożonych jednostaj-    [(Pi + Pi) ₃ +•♦ ] + _g, [^J + i + *> ł]

nie na całej długości słupa ramy nierdwnoramiennej (rys. 7). Mianownik powyższego wyrażenia jest widocznie identycz-Odpowiednie V znajdziemy kładąc po prawoj stronie pierw- _{ny z} mianownikiem we wzorze (IV). Nadto wypływa z waszego z wzorów (HI, 1) gdy = r/ldg zamiast Pi całkując od runków równowagi:

S, = 0(i)=0)doy=łi₁ (i) = ł,). A zatem    B, = qh — H, )

czyli po wykonaniu całkowania i uproszczeniu:

j[| ł»(ł.+ł.)+p.ł.^,+ps+,^,-|pA^,‘gp]+ + £ [l+(*.' + ».')♦,]} • ■ • • (V,l),

przyczem wartość mianownika p. jest ta sama, co we wzorach (I) do (III).

Analogicznie wypada dla obciążenia z prawoj strony:

|[l ł, W.+-W+P,ł,*4f»łi^,+|p.ł.^,‘«pj+ + “.[l+ (<+**')♦.]]• • • • CV,2). Łatwo przytem dostrzedz, że pierwsze wyrażenia w klamrach są zależne wyłącznie od momentów zgięcia, drugie zaś tylko od sił poprzecznych i podłużnych.

Z warunku momentów sił zewnętrznych względem punktu A i B wypada teraz

B,(h_l-hj_l = q'^ -VI,

*i (*i

-a,)=₈a,((*,-)!,- |‘) + n,

(1 +1, cotg P) + V cotg P j t, — pj cotg p

(20). “Ibo po wprowadzenia obciążenia całkowitego

R = J ?,A,

i podstawieniu A, = (f,, y = Ig :

♦./........

Podstawiając teraz po prawej stronie wzoru (III, 1)

P = q dy = qldg =......

i całkując w granicach ę = 0 i i| = <ji„ znajdziemy po licznych redukcyach:

= “g - ^ [y łi (łi + łjH- Pi łi* + Pj ł,' —

-Jawan+r*] ■ - . .<TO1>

Analogicznie będzie dla obciążenia z prawej strony:

r» = "" A["

2    ⁽+i + +j) + Pi łi" + Pi V +

+ ggP>ti^ł*gP-|-W'j- • • •

(VII, 2),

ustalone

Moment zgięcia w dowolnym przekroju y słupa AC

M = //,!/ — ę ......(21

osiągnie największą wartość dla y = —¹ (wtedy bowie ^ = 0i t d.), która zatem będzie:

przyczem wielkości k‘„., .. „ powyżej w równaniach (III).

Z warunku momentów względom przegubu A i B otrzy-

-A(?A, — A,) + ff, (A, - Aa) - Pł = = l®(lłi —łi) +F] cotgp.l