2999072762

Jeżeli do lewych stron nierówności dodamy odpowiednio takie liczby nieujemne ^Xn+i ’ ^xn+2>    ^xn+m * by warunki te przybrały postać następujących równań:

auxx	+ anx2	+ ...	+ alnxn		II J3*
a2ixx	+ a22x2	+ ...	^+ a2n^Xn		li _C3-
^aml^Xl	+ am 2^X2	+ ...	+ amnxn	+ x„m	= bm

to przekształconą postać standardową zadania programowania liniowego nazwiemy postacią kanoniczną. Dodatkowe zmienne x_n+l > 0, x_ll+2 > 0, x_n+m >0 nazywają się zmiennymi bilansującymi.

Warunki ograniczające [2.2] lub [2.5] wyznaczają w n-wymiarowej przestrzeni 9Tobszar D decyzji dopuszczalnych (d_i,d₂, ..., d_n). Inaczej mówiąc, każda kombinacja wypukła d„ (Xj), będąca rozwiązaniem układu równań lub nierówności ograniczających [2.3] lub [2.5] i spełniająca warunek nieujemności, tworzy obszar zawierający zbiór rozwiązań dopuszczalnych. Obszar ten może być ograniczony, nieograniczony lub może być zbiorem pustym, gdy układ nierówności [2.2] jest sprzeczny.

Zadanie programowania liniowego możemy również przedstawić wektorowo. Klasyczna (standardowa) postać zadania PL w zapisie wektorowym wygląda następująco: cx —> max    [2.8]

Ax < b    [2.9]

x > 0    [2.10]

gdzie:

c - wektor wierszowy współczynników funkcji celu

c = [c,,c₂,...c_n]

x - wektor kolumnowy zmiennych decyzyjnych x = [x,, *₂ ,...*„]

A - macierz współczynników warunków ograniczających a_n a_l2 ... a_ln

a_m, a_m2 ... a_nm

b - wektor kolumnowy wyrazów wolnych (prawych stron warunków ograniczaj ących)

W

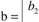
b_m

Postać kanoniczną PL przedstawimy z kolei w sposób następujący: cx —> max    [2.11]

Ax = b    [2.12]

x > 0    [2.13]

12