3702672302

[86]

Maciej Major, Barbara Nawolska

3. Propozycja uogólnienia gier Penneya

W niniejszej pracy zaproponujemy kolejne - inne niż dotychczas - uogólnienie gry Penneya.

Ustalmy dwie serie orłów i reszek a oraz 6, każda o długości k. Rozważmy grę z udziałem dwóch graczy G i i G2- Każdy z graczy czeka na jedną z ustalonych serii, np. gracz G\ na serię a, gracz G^ na serię b. Gracze równocześnie rzucają monetami, każdy własną, i obserwują wyniki swoich rzutów. Równoczesny rzut monetami powtarzają tak długo, aż któryś z nich doczeka się swojej serii orłów i reszek i wówczas on zwycięża. Gdy obaj gracze jednocześnie doczekają się swoich serii, gra kończy się remisem. Opisaną grę oznaczmy symbolem g_a|&.

Zauważmy, że w tej wersji gry, inaczej niż ma to miejsce w przypadku oryginalnych gier Penneya czy też wspomnianych wcześniej uogólnień, gra może zakończyć się remisem. Ponadto, co wcześniej nie miało sensu, gracze mogą czekać na tę samą serię. W takim przypadku gra nie musi zakończyć się remisem - choć (co łatwo zauważyć) jest grą sprawiedliwą.

Symbolem <5_a|& oznaczmy doświadczenie przeprowadzane w grze g_a\b- Wyniki tego doświadczenia są parami ciągów ((a_n), (&„)) co najmniej fc-wyrazowych o"takiej samej liczbie n wyrazów. Pierwszy ciąg prezentuje wyniki kolejnych rzutów gracza Gi, drugi - gracza Gn- Ponadto k ostatnich wyrazów ciągu (a_n) tworzy serię a lub k ostatnich wyrazów ciągu (b_n) tworzy serię b.

Oznaczmy zbiór wyników doświadczenia <5_a|f, symbolem fi_a|fc. Jeśli u; G Q_a\b i"uj jest parą ciągów n-wyrazowych ((a_n), (6_n)), gdzie n ^ fc, to jego prawdopodobieństwo jest równe • ^r, czyli (^)ⁿ. Wynika stąd, że modelem² doświadczenia J_a|6 jest para (^_a|6łPa|f>)> gdzie p_a\b jest funkcją określoną wzorem:

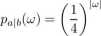
gdzie |w| oznacza liczbę wyrazów ciągów zarówno (a_n) jak (b_n), czyli ich długość. Z doświadczeniem losowym S_a\b zwiążmy trzy zdarzenia:

A = {doświadczenie S_a\b zakończy się uzyskaniem serii a (serii gracza Gu)},

B = {doświadczenie J_a|i, zakończy się uzyskaniem serii b (serii gracza G2)},

R = {doświadczenie <5_a|& zakończy się równoczesnym uzyskaniem serii a oraz 6},

które oznaczamy A = {... a|*}, B = {...* \b} i R = {... a|&}, a ich prawdopodobieństwa odpowiednio przez P{... a|*), P{... * |6) i P(... a\b).

Jeśli P(...a|*) = P(... * |6), to serie a i b nazywamy jednakowo dobrymi i oznaczamy a ~ b.

Jeśli P(... a|*) > P(... * |6), to serię a nazywamy lepszą od serii b i oznaczamy a » b.

W zbiorze serii orłów i reszek o długości k określone zostały zatem dwie relacje: « i ».

^!Zob. (Płocki, 2004), rozdział 2.