372596236

29

RIKEN Accel. Próg. Rep. 24 (1990)

111-1-19. Dissociation Cross Sections of ⁿLi

K. Soutome, S. Yamaji, and M. Sano

[dissociation of ⁿLi, target-charge dependence, Glauber approximation.)

Recently, Kobayashi et al.^l) measured cross sections for the reaction ¹¹ Li + TC4_t,Z_t) —► ⁹Li + X where T = C, Cu, and Pb and reported unusual target-charge dependence of the Coulomb dissociation cross section o_c^(exp). In extracting o_c^(exp) from experimental data o^(exp), they assumed that (i) the nuclear dissociation cross section ON^(exp) takes the form o_N^(exp) = y{R(^uU) + R(T)}, where R(A) is the “interaction radius”²⁾ of a nucleus A and (ii) Coulomb-nuclear interference can be neglected and hence o^(exp) = o_c^(exp) + o_N^(exp), and (iii) o_c^(exp) = 0 for T = C. With these assumptions they first fixed y using the value of o^(exp) for T = C and then calculated o_N^(exp) for T = Cu and Pb from which o_c^(exp) _a(exp) __ _ON(exp) _{can es}ti_mated. In this way, they obtained the target-charge dependence o_c^(exp) Z_r^141±0-²², which deviates largely from Z_T².

Assuming that ¹¹ Li consists of a ⁹Li core and two valence neutrons and the core remains in its ground State after collision, we can calculate the dissoscia-tion cross section for the above process using Glauber s formalism. Computational details are given in Ref. 3 and here we show only numberical results in Fig. 1. Our nuclear cross section o_N (dotted curve) shows a qualitative agreement with ON^(exp), while the total cross section o (dashed curve) overestimates for a Pb target. This is due to the fact that the effect of Coulomb-nuclear interference is — as expected — smali and hence o-o_N is almost equal to the pure Coulomb cross section o_c, which rises as Z_x².

As discussed in detail in Ref. 4, however, the exponent of the Coulomb cross section o_c is sup-pressed for a high-Z_T target if we take account of the bending of a trajectory. The solid curve in Fig.

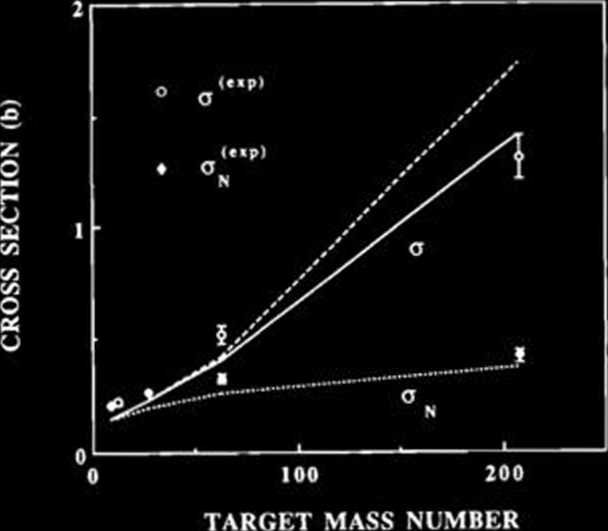
Fig. 1. Dissociation cross sections calculated and measured for ¹¹ Li. The dashed curve represents the total dissociation cross section o calculated by a harmonie oscil-lator model,³⁾ and open circles are the cross sections measured o^(exp). Cross sections due to pure nuclear interaction o_N are also shown (dotted curve) together with the experimenta! o_N^(cxp). The solid curve represents the cross section o which takes bending effects into account.¹’

1 includes this effect. In this case the Z_x dependence of the Coulomb cross section becomes Z_t^L75, closer to the experimental Z_T dependence. This shows the limits of the straight-line approxima-tion, or the importance of the bending effect.

References

1)    T. Kobayashi etat.: Phys. Lett., 232B, 51 (1990).

2)    1. Tanihata et al.: Phys. Rev. Lett., 55, 2676(1985).

3)    K. Soutome, S. Yamaji, and M. Sano: RIKEN-AF-NP-96 (1990).

4)    K. Soutome, S. Yamaji, and M. Sano: in preparation.