372596237

RIKEN Accel. Próg. Rep. 24 (1990)

111-1-20. Induced Fission Studied with a Multi-Dimensional

Langevin Equation

T. Wada, Y. Abe, and N. Carjan¹

I Fission, multi-dimensional Langevin eguation, kinetic energy distribution.)

Nuclear dissipative phenomena, such as deep inelastic collisions, have been treated as non-equilibrium statistical problems. Slow collective degrees of freedom with heavy masses are treated as Brownian particles and fast nucleon degrees of freedom as a heat bath. It is shown in Ref. 1) that recent developments in computers enabled us to practically solve a Langevin equation. As is well known, nuclear fission is a multi-dimensional collec-tive motion. Some observable quantities are expected to reflect multi-dimensional dissipative dynamics. Thus it is very important to extend Langevin approach to multi-dimensional cases.

A multi-dimensional Langevin equation is given by

d „ dV 1 d _/    .

dt^P' = - dq]~ 2^p> dq,^(m >***

^jkPk+gijRjit)

dt^q' ^{= {m V)}"^p’    (1)

where m_tJ and y,y are the mass and friction tensor, respectively. The multi-dimensional random force R,(t) is assumed to be a white noise and its strength g# is given by g_ikg_jk = Ty_ijt where T is the temperaturę of a compound nucleus.

A characteristic aspect of the Brownian picture for nuclear fission is a fluctuation of the fissioning coordinate in the course of the descent from saddle to scission, which are expected to strongly affect observable quantities of fragments, such as kinetic energy distrubution. 'fhe fragment kinetic energy is calculated as the sum of the pre-scission kinetic energy and the Coulomb energy between two fragments at scission. In one-dimensional treatment, the yariance of the kinetic energy comes only from the fluctuation of the pre-scission kinetic energy, because the scission point is fixed. Calculated vari-ance was found to be too smali to explain experi-mental data. On the other hand, in a multi-dimensional treatment, the fluctuation of the scission point causes the fluctuation of the Coulomb energy. Several authors have already tried to explain the large variance by solving a multi-dimensional Fok-ker-Planck equation approximately and obtained rather satisfactory results.^2> Here we directly solve the multi-dimensional Langevin eguation (1) without any approximations. 'fhe potential V(q), the mass tensor 7), and the friction tensor y,j(q) are calculated with a iiquid drop model.^%i) We adopt two-body dissipation mechanism in calculating y,j(q) with a viscosity coefficient /jl = 0.02 TP = 1.25 x 10^-2** MeV-s/fm¹. Figurę 1 shows the calculated

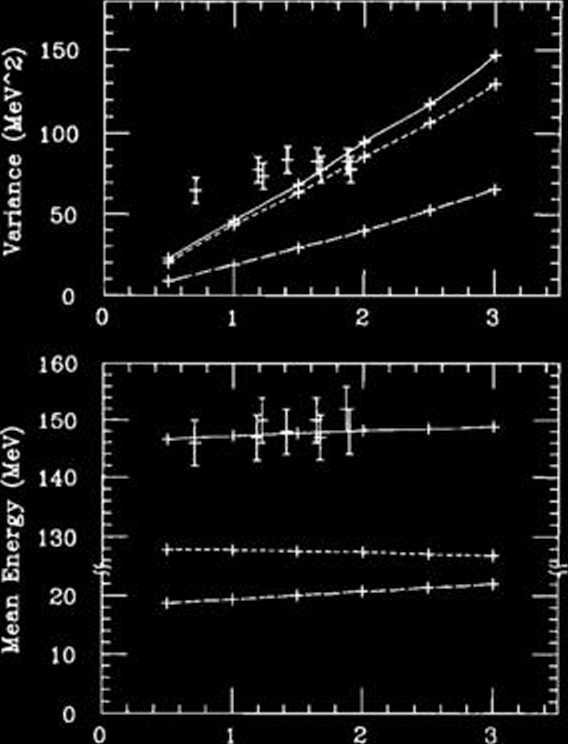
Temperaturę (MeV)

Fig. 1. Average value of the fragment kinetic energy and its variance are compared with experiment for the sym-metric fission of ~^uAt. Long dashed lines are for the pre-scission kinetic energy, short dashed lines are for the Coulomb energy, and solid lines are for the total kinetic energy. Experimental values are taken from Ref. 4).

average value of the fragment kinetic energy and its yariance as a function of the nuclear temperaturę for the symmetric fission of ²UAt. 'Fhe agreement between the theory and the experiment¹⁾ is very good for the average value of the kinetic energy. 'Fhe calculated yariance is found to be dominated by the fluctuation of the Coulomb energy.

References

1)    Y. Abe et al.: J. de Phys. (Parts), 47, C4-329 (1986).

2)    F. Scheuter et al.: Phys. Lett., 149B, 303 (1984); (i.D. Adeev and V.V. Pashkevich: Nuci. Phys., A502, 405c (1989).

3)    K.T.R. Davies et al.: Phys. Rev., C13, 2385 (1976); H.J. Krappe et al.: ibid., C20, 992 (1979).

4)    F. Plasil et al.: ibid., 142, 696 (1966).

1

Centre cTEtudes Nucleaires, Bordeaux-Gradignan, France.