4189283850

Modelowanie rzeczywistości geograficznej w systemach informacji przestrzennej 51

tościowym zapisem przejściowym uzyskiwanym w czasie pomiarów terenowych, materiałem źródłowym, podlegającym porządkowaniu w procesie opracowywania wyników. Jest to godne podkreślenia tym bardziej, że na podstawie dostępnej literatury nie udało się potwierdzić tej roli modelu spaghetti.

Model topologiczny elementarny

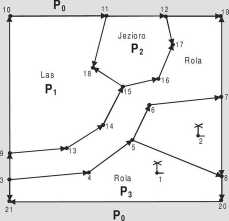
Rys. 5. Struktura obrazu mapy zapisana jako model topologiczny elementarny - załamania i powiązania linii tworzą węzły, pary węzłów wyznaczają jednostki strukturalne obrazu - wektory

W zastosowaniach związanych z technologią systemów informacji przestrzennej termin topologia stworzony jest do określenia relacji pomiędzy obiektami obrazu mapy. W modelu topologicznym elementarnym wszelkie punkty załamania linii łamanych oraz punkty styku trzech i większej liczby linii oznaczamy jako węzły (rys. 5). Wektory tworzą powiązania pomiędzy węzłami.

W przypadku obiektów powierzchniowych zapis relacji pomiędzy obszarami obejmuje nie tylko obiekty wycinka mapy. Zapis ten musi również uwzględniać obszar znajdujący się poza ramką wycinka, ponieważ sąsiaduje on z obiektami wewnętrznymi. Obszar zewnętrzny traktowany jest jako nieskończona przestrzeń 2-D, otaczająca granice rysunku (na rys. 5 oznaczona jako

obszar P_Q). Topologia obszarów zakłada wyróżnianie w nieskończonej przestrzeni obszarów utworzonych z powiązanych ze sobą wektorów. Łańcuchy wektorów muszą tworzyć układy zamknięte.

Obiekty liniowe, reprezentowane przez wektory, posiadają również swoje relacje topologiczne w stosunku do obszarów i węzłów. Węzły posiadają relacje z powiązanymi z nimi wektorami. Obiekty punktowe, które nie stykają się z żadnym z wektorów, traktowane są jako tak zwane węzły izolowane (nr 1 i 2 na rys. 5).

W modelu wektorowym elementarnym występują trzy zapisy: zapis odniesienia przestrzennego i struktur elementarnych, zapis topologii oraz zapis obiektów.

Zapis przestrzennego odniesienia i struktur elementarnych

Zapis przestrzennego odniesienia jest identyczny jak katalog współrzędnych punktów zawarty w tabeli 1, jednak z taką różnicą, że w obecnym modelu wszystkie punkty są traktowane jako węzły, niezależnie od tego czy są powiązane z wektorami, czy też są węzłami izolowanymi. Podobnie jak w modelu wektorowym nietopologicznym także i tutaj dokonuje się zapisu wektorów opartych na dwóch punktach, początkowym i końcowym, analogiczne jak w tabeli 2, jednak w tym przypadku punkty zastąpione są węzłami.