5109637439

spełnione są jeśli węzły wewnątrz komórki tworzą z trzema najbliższymi węzłami podstawy czworościan formny. Oznaczając długość krawędzi czworościanu przez a natychmiast możemy określić wysokość jego podstawy, która jest równa ^-a. Wysokość w graniastosłupie dotyka podstawy w punkcie, kóry znajduje się w | wysokości podstawy, licząc od krawędzi. Z równości Pitagorasa wyznaczamy więc wysokość czworościanu h = \f\ci. Całkowita wysokość komórki elementarnej (pokazanej na poprzedniej stronie) jest oczywiście dwukrotnie wyższa, czyli c = y/Ęa- Ostatecznie stopień upakowania sieci hep wyznaczamy, wiedząc iż promień kul jest równy połowie długości krawędzi czworościanu R — |a. Zbierając wszystkie powyżej przedstawione szczegóły otrzymujemy objętość komórki elementarnej Vk_om — c ■ S_po(i_st = c - 6 •    — c ^a?

stąd odpowiedni stopień upakowania wynosi

ĄttR?    1    7T

a = 6-    ——    =    —j=    ~ 0.74048054377754013.    (3)

3    vkom    3v2

Kolejnym ciekawym przykładem jest struktura krystalograficzna utworzona przez atomy węgla związane silnymi wiązaniami kowalencyjnymi. W wariancie trójwymiarowym wiąznia kowalencyjne prowadzą do struktury diamantu (rysunek poniżej) natomiast w przypadku dwuwymiarowym do heksagonalnej struktury grafenu. O strukturze grafenowej będziemy szczegółowo mówić w dalszej części wykładu, teraz zajmiemy się zaś przypadkiem diamentu.

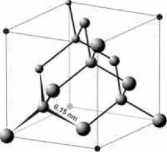
Struktura diamentu. Atomy węgla znajdują się w narożnikach sześcianu i na środku każdej z płaszczyzn, zaś cztery dodatkowe atomy znajdują się wewnątrz komórki elementarnej.

Silne wiązania kowalencyjne atomów węgla w diamencie są spolaryzowane przestrzennie. Aby określić kąt między tymi wiązaniami rozpatrzmy powyżej przedstawioną komórkę elementraną, koncentrując uwagę na lewym dolnym narożniku. Atom węgla znajdujący się wewnętrz komórki

6