5484453281

odbicie od białej kartki jest bardzo jasne dla ludzkiego oka. Czas po którym obwiednia jest mnożona przez czynnik e^-1 « 0,37 to r = 23fs. Można przyjąć, że impuls trwa 2r = 46fs, gdyż w tym czasie znajduje się > 99% przenoszonej przez niego energii. Z akurat takiego rzędu czasu 10^-15s = 1 fs przyjęło się nazywać omawiane lasery femtosekundowymi. Nic teraz nie stoi na przeszkodzie, by pokusić się o policzenie chwilowej mocy:

Pimr = pf Pimp = 8,6 • 10^lW

Biorąc pod uwagę średnicę wiązki, przyjmimy r = 2mm, chwilowa równowaga zaszła by z ciałem doskonale czarnym o temperaturze ~ 26kK. Warto zwrócić jednak uwagę, że istnieją sposoby, by T było rzędu miliherców - co pociąga za sobą olbrzymie moce chwilowe!

4 Ciekawe impulsy

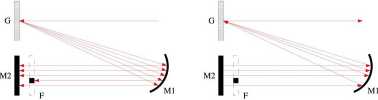
Czy istnieje jakiś w miarę prosty sposób na modyfikację widma? Okazuję się, że tak. Montując, jak na [rys. 3], układ z siatki dyfrakcyjnej, lustra wklęsłego i płaskiego wiązka rozszczepia się ze względu na widmo, po czym ponownie łączy. W takim ustawieniu nic się specjalnego nie dzieje. Ale gdy przy samym płaskim zwierciadle umieści się kawałek nieprzeźroczystego materiału, pochłania on część widma.

a)    b)

Rysunek 3: Schemat układu umożliwiającego wybiórcze wycinanie widma. G - siatka dyfrakcyjna, Ml - lustro wklęsłe, M2 - lustro płaskie, F - miejsce w które można włożyć filtr. Wiązka wchodząca a) i wychodzące b) są oznaczona czerwonym kolorem. Kąt padania jest wiązki na M2 jest bliski prostemu, jednak nie jest jemu równy, co umożliwia rozdzielenie wiązek wchodzącej od wychodzącej.

Obcinając pewne części funkcji Gaussa powstają widma o kształcie łatwo przybli-żalnym do prostych figur. Zwracam jednak uwagę, że obcinając widmo, jest ono węższe, a zatem i impuls powinien być dłuższy. W rzeczywistych przypadkach liczba oscylacji w czasie trwania takich sygnałów jest większa niż dla czystego sygnału.

4