5521243835

Ks 48

PRZEGLĄD TECHNICZNY

1013

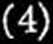
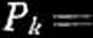
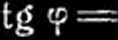
czyny wykrzywiającej może odegrać np. chwilowa różnica temperatury na dwóch przeciwległych powierzchniach pręta, albo też pewne momenty lub siły poprzeczne, tak małe, aby naprężenia przez nie wywołane, mogły być uważane za 0 w porównaniu z naprężeniem-.-, a więc i z naprężeniem:

gdzie A jest to pole przekroju, W—wskaźnik wytrzymałości pręta, P* — siła krytyczna, y[— największe wygięcie pręta,

'Powyższe określenie dotyczy prętów doskonale sprężystych, natomiast w słupach stosowanych w budownictwie, po przekroczeniu przez siłę podłużną wartości krytycznej i po wykrzywieniu się słupa, naprężenie (I) przeważnie przekracza granicę wytrzymałości i słup ulega złamaniu. We wzorze (1) jest więc, według słów Colli-gnon‘a *), drugi wyraz 'jego prawej części tym mieczem Damoklesa, który zawisa nad prętem prostym, z chwilą, <gdy siła podłużna osiąga wartość krytyczną.

2°) Wyboczenie niesprężyste. W danym razie za siłę krytyczną należy uważać najmniejszą wartość osiowej siły podłużnej, przy której każda przyczyna wykrzywiająca, w sensie omówionym pod 1°, wywołuje trwałe odkształcenie .pręta, czyli jego złamanie. W tym wypadku nie może być mowy o sprężystej krzywoliniowej formie równowagi pręta, gdyż siła krytyczna wy

wołuje tu naprężenia

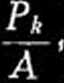
przekraczające granice

sprężystości jeszcze przed zakrzywieniem.

Ponieważ obliczenie siły krytycznej nie może się w danym wypadku opierać na twierdzeniach teorji sprężystości, musimy tę siłę wyznaczać drogą doświadczalną. Ze względu na niedoskonałość aparatury doświadczeń, siła podłużna P w badanym pręcie działa zazwyczaj mimośrodkowo, wskutek czego przyczyna wykrzywiająca pręt zaczyna tu działać w rzeczywistości nie w chwili, gdy siła P dosięga wartości krytycznej, lecz już od chwili przyłożenia tej siły. W ten sposób mamy w danym razie do czynienia właściwie z jednoczesnem ściskaniem i zginaniem, a wyznaczona doświadczalnie siła P różni się od' właściwej siły krytycznej tem więcej, im większy jest jej mimoś-ród, który nam nie jest jednak znany i w obliczeniu uwzględniony być nie może.

3°) Ściskanie m i m o ś r o d >k o w e. Wobec tego, że zasada superpozycji w danym wypadku przeważnie nie może mieć zastosowania do prętów żelaznych, więc jest to, jak poprzednio, wypadek tak zwanego .jednoczesnego ściskania i zginania, z tą jednak różnicą, że mimośród siły podłużnej jest tu wiadomy. Zagadnienie sprowadza się do obliczenia wymiarów pręta na podstawie znanej siły ściskającej i jej mim oś rodu, oraz do porównania naprężeń, otrzymanych w poszczególnych częściach pręta, z naprężeniami, dopuszcza 1-nemi w prętach ściskanych i zginanych jednocześnie.

⁸) Ed. Collignon, Flcxion des pieces droites coraprimees, Annales des ponts et chaussees, 1889.

(W zależności od powyższego, można podzielić sposoby obliczenia prętów złożonych na trzy grupy.

'Pierwsza grupa metod obejmuje prace Timo-szenki"), Elwitz‘a ^I0), Engessera ”), PrandtTa ^1U) i in. Wszystkie one rozpatrują wyboczenie sprężyste prętów złożonych, doskonale prostych i obciążanych ściśle osiowo. Zastosowanie wzorów, wyprowadzonych dla podobnych prętów, poza granicami sprężystości natrafia na trudności i może mieć miejsce jedynie przy zastosowaniu dużego spółczynnika bezpieczeństwa lub przez wprowadzenie pewnych spółczynników doświadczalnych.

■Przykładem prac tej -grupy mogą być prace Engessera, który wogóle pierwszy ogłosił obliczenie słupów złożonych (r, 1891). Rozważał on zarówno słupy kratowe, jak i ramowe, przyczem u-ważał, że -poszczególne pasy shi-pa nie są rozcięte. Engesser wyraża ugięcie pręta w razie jego wykrzywienia zapomocą sumy następującej:

y=y' + y".......(²)

gozie y' oznacza część ugięcia, wywołaną przez moment zginający, a y” — część wywołaną przez siłę poprzeczną. Engesser uważa, że zarówno y, tak y' i y" zmieniają się wzdłuż pręta wedłęg prawa ccsinusa (przy początku s pół rzędnych w środku długości pręta), przyczem rzędne cosinusoid znajdują się do sielbie w stosunku proporcjonalności. Jeżeli ^CJ- oznacza spółczynnik proporcjonalności, mamy, że:

y‘ = cj.y i yⁿ = (1—o) y ....    (3

Wyprowadzając wzór siły krytycznej dla prę-) ja o możliwych ugięciach y¹ w ten sam sposób, jak się go wyprowadza dla sprężystego pręta pełnego, dochodzi Engesser do wzoru, dla siły krytycznej :

a El ~

2

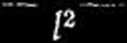
O ile kąt <p (rys. 5) oznacza nachylenie odcinka pasa pręta złożonego, wywołane działaniem siły poprzecznej, to

__Oj_

Ef cos²i»> sin

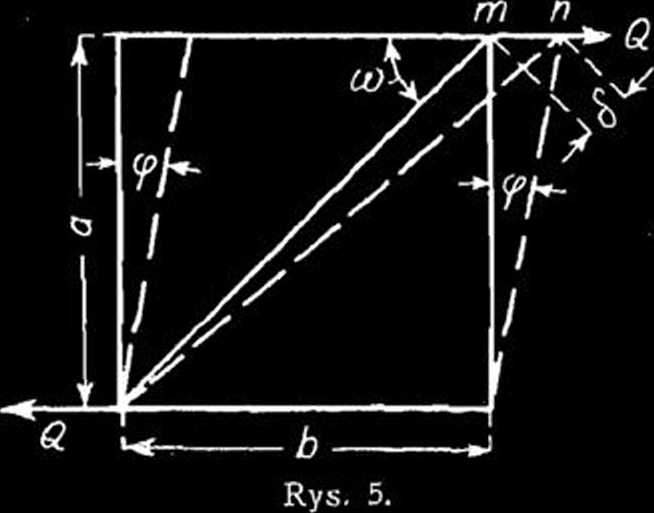
gdzie Q oznacza silę poprzeczną w pręcie, a / ,po

^,J) S. Timoszenko. Wytrzymałość Materiałów, Iłómaczenie M. Huhera.

^l0) E. Elwitz. Dic Lehre von der Knickfestigkeit, 1920. ^,ł) Fr. Engesser. Uber die Knickfestigkeit gegliederter Stabe, Zentralbhilt der Bauverwaltung 1891, 1909.

^1?) L. Prandll. Knickfestigkeil von Gitierslaben, Zeit-schrift des Yereines deutscher Ingenieurc, 1907.