5521243840

Ne 48

PRZEGLĄD TECHNICZNY

1015

—>

^— dx»'

liczbę równań, wyrażających bądź zależność między momentami zginającemi a siłami działające-mi w poszczególnych częściach pręta, bądź też zależność między odkształceniami. W szczególności kąty <p oblicza on z równania różniczkowego:

El^=~O_m';r\-M°_m-\-S_mx,    . . (15)

gdzie v) jest to- wywołane wyginaniem się pasa przesunięcie poszczególnych punktów jednego przedziału względem prostej, łączącej punkty węzłowe, obejmujące dany przedział.

Wobec tego, że przy x = 0, i\=y_m~ym-u gdzie y oznaczają przesunięcia się węzłów, wzór dla <p_m nie będzie już zawierał rzędnej . W podobny sposób zostają wyrażone przez y_m również i kąty a oraz r. Wreszcie drogą przekształceń algebraicznych dochodzi Muller - Breslau do szeregu równań różnicowych, wyrażających zależność między kolej-nemi wielkościami :y_m_2, ym~i, ym+i i y™+2.

Są to równania typu następującego;

yn,-2 x — y„,-i (1 + x) + 2 (1 — x — *') —

— y_m+\ (\~\~x)-Ą-y_m+2 x'= A xa    . . . (16)

•Wielkości x' i x wyrażają stosunki między poszczególnemi wielkościami zadania i są uważane za liczby stałe. Równania (16) dają możność wyznaczenia wszystkich y_m. Dla umożliwienia sobie rozwiązania tych równań, zakłada Miiller-Bre-slau, że ym zmienia się według paraboli, co, łącznie z innemi założeniami upraszczającemi, niweczy tę ścisłość, z którą autor postawienie kwestji traktuje.

W podobny sposób rozwiązuje Miiller-Bre-slau również i zadanie prętów ramowych. Przy ci = 0 wzory Miiller-BreslatPa nabierają cech wzorów Engessera, Timoszehki i innych wzorów tej grupy*

Zaproponowany przeze mnie sposób obliczenia prętów złożonych, ściskanych mimośrodkowo polega na następującem ^lrt).

Rozważamy wypadek, gdy siła podłużna R przecina oś pręta, wobec czego siła ta rozkłada się wzdłuż pasów nierównomiernie. Liczymy się z tern, że pasy są nierozcięte na całej długości pręta i że krata jest z paisami połączona przegubowo.

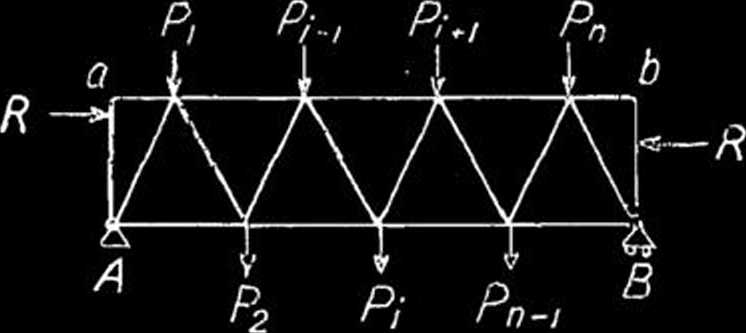
Rys- 7.

Bierzemy pręt, przedstawiony na rys. 7, i o-znaczamy przez P siły wzajemnego oddziaływania. na siebie kraty i pasów pręta, skierowane prostopadle do osi pasów. Pod działaniem sił P i siły

^,6) W. Wierzbicki, O wytrzymałości prętów złożonych w mostach żelaznych, 1924, Warszawa, wyd. Min. W. R. i O. P.

podłużnej R, węzły pręta przesuwają się w kierunku prostopadłym do osi w ten sam sposób, jak węzły kratownicy przegubowej. Odpowiednie przesunięcia oznaczamy przez y^p oraz y^R.

Rys. 8.

Z drugiej strony, obliczamy przesunięcia pasa y^c, jako ugięcia belki swobodnie podpartej w obydwóch końcach i obciążonej jednocześnie siłami prostopadłemi do osi (P) i siłami podłużne-mi (rys. 8).

Ugięcia te otrzymujemy ze wzoru;

— = M^P — M^R......(17)

P

gdzie M^p i M^R oznaczają odpowiednie momenty zginające sił poprzecznych i sił podłużnych. Ponieważ zcałkowanie równania (17) natrafia na

trudności bardzo wielkie, zakładamy, że — = tłomacząc to tern, że w danym wypadku

pasy znajdują się w warunkach podobnych do prętów, leżących w środowisku sprężystem, i dlatego nie ulegają zbyt wielkim ugięciom. Siły podłużne uważamy w każdym przedziale pręta za znane, choć różne od siebie, zaś siły P wyznaczamy z równań;

y^ct — yf+yf......l¹⁸)

które wyrażają, że przesunięcia węzłów pręta złożonego, jako węzłów kratownicy, muszą być równe przesunięciom pasów pręta, jako belek zginanych.

W rozwiązaniu powyższem główną trudność stanowi obliczenie pasa, jako pręta jednocześnie zginanego i ściskanego. Trudność tę usuwamy, wprowadzając przybliżony sposób obliczenia prętów zginanych, oparty na metodzie Rilz‘a i Tinio-szenki¹⁷), która, zdaniem, tego ostatniego, może być (z pewnemi zresztą zastrzeżeń ki mi) stosowana i do prętów, ulegających jednocześnie zginaniu i ściskaniu, a więc i do pasów prętów złożonych.

Obliczenie prętów ramowych różni się od obliczenia prętów kratowych głównie wprowadzeniem momentów, wyrażających oddziaływanie poprzeczek na pasy.

Przytoczone ostatnio obliczenie pozwala na możliwie najlepsze uwzględnienie wszystkich warunków pracy pręta złożonego.

iMimośród siły podłużnej, w prętach mostowych, może być obliczony ściśle przy uwzględnieniu sztywności węzłów kratownicy mostowej. Przezemnie został on przyjęty na podstawie prac

^,7) W. Ritz, Ueber eine neue Methodc zur Losung ge-wisser Variationsprobleme der mathematischen Physik, Journal fur reine und angewandte Mathematik. 1909. S. Timo-szenko. ob. wyże].