5783291369

6 Odwrotne zadanie kinematyki

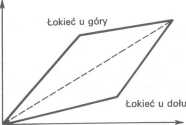
Rysunek 2.1: Proste zadanie kinematyki - opis w tekście

C2 = cose2 = * H-t-4-4 2aia2	(2.1)
zatem ©2 jest równe:
©2 = arccos(C2)	(2.2)
Mając na uwadze postać konfiguracji „łokieć u góry” i „łokieć u dołu”, można wyprowadzić zależność algebraiczną dającą możliwość rozróżnienia obu członów robota:
sin(02) = ±(\/l - C|),	(2.3)
©2 = ar etan--—. O2	(2.4)
y2 a2sin(@2) ©1 = ar etan--ar etan-. _ ., X2 ai+02C0S(©2j	(2.5)