660358787

wzrost kosztów produkcji. Jest to założenie całkowicie dowolne, przyjęte dla uproszczenia dalszej analizy matematycznej, w której zakłada się, że czasy czynności podawane do wykreślenia grafu sieciowego odpowiadają idealnemu stanowi organizacji pracy. Omawiając metody analizy sieciowej kosztów wykonania jako funkcji czasu, przyjmiemy, choć z zastrzeżeniami, założenie, że czas normatywny t_n odpowiada najniższej wartości kosztów wykonania K_inin. Skracanie czasów wykonania poszczególnych czynności jest ograniczone względami technologicznymi i czynienie tego poniżej wartości t_gr nie jest możliwe. Koszt wykonania czynności w jej czasie granicznym wynosi K_gr.

Dla dalszego uproszczenia analizy sieciowej kosztów wykonania w zależności od czasu jej trwania przyjęto w miejsce parabolicznej krzywej K_c = f (t) przebieg liniowy (rys. 1.12).

Rys. 1.12. Liniowy przebieg zależności kosztów wykonania od czasu trwania czynności.

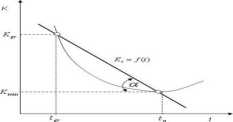
Wprowadzając liniowy przebieg funkcji K_c = f (t), można znacznie uprościć zagadnienie przez założenie stałego przyrostu kosztów na jednostkę czasu, tzw. średni gradient kosztów s:

tg cc = -

Wreszcie można przedstawić w uproszczonej postaci funkcję kosztów K_e jako równanie linii prostej:

[39] = f(t)

K, =(K_nin + s • t_n) — s • t

[40]

Podstawiając

b=(K_mi„+s-t_n)    [41]

otrzymamy znane równanie linii prostej:

K, =b-s-t    [42]

Gradient kosztów s wyraża się w zł/jednostkę czasu czynności jest różny dla różnych czynności. Stąd ogólne równanie kosztów różnych czynności y_y w sieci zależności przedstawia się:

K, = by - Sy • ty    [43]

przy czym:

t„ >t >t_f

[44]

12