7193935652

AKTYWNE ZAWIESZENIE WAHADŁOWEGO ELIMINATORA DRGAŃ

lator), co jest wykorzystywane w dynamicznej eliminacji drgań [7, 9] lub w odzyskiwaniu energii [6j.

Badania numeryczne przeprowadzono za pomocą metody kontynuacji na podstawie równań [3] i [4]. Metoda ta uwzględnia występowanie bifurkacji postaci oraz utratę jej stabilności. W celu zastosowania techniki kontynuacji, wymagana jest znajomość rozwiązania okresowego. Wykonywane jest jedno całkowanie rozwiązania okresowego za pomocą metody Rungego-Kutty czwartego rzędu, a następnie rozwiązanie to jest korygowane za pomocą metody Newtona-Raplisona [1],

Badania numeryczne wykonano na danych zidentyfikowanych na stanowisku badawczym:    a_t = 0.26,

a₂ = 0.1, n = 17.23, X = 0.13.ą = 1. Wszystkie warunki początkowe były równe zeru, oprócz początkowego wychylenia wahadła, które wynosiło <p = 0.1.

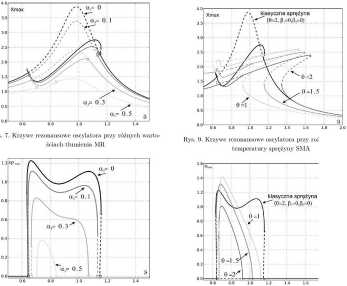
drgań zachodzi przy częstości wymuszenia 9»0.7. Aktywowane tłumienie MR, powoduje zmniejszenie maksymalnych amplitud drgań, zarówno rozwiązań stabilnych jak i niestabilnych. Ponadto tłumienie MR nie powoduje zaniku zjawiska dynamicznej eliminacji drgań, lecz jedynie ograniczenie zakres rezonansu -obszar dynamicznej eliminacji drgań jest zawężony (rys. 7). Przy dużej wartości a₃ = 0.5, istnieje bardzo mały zakres rezonansu, gdzie obseiwujemy efekt absorpcji drgań. Tłumienie MR znacznie redukuje amplitudę wahadła (rys. 8). Należy zauważyć, że redukcja rezonansu następuje z prawej strony krzywej, jednocześnie obszar dynamicznej eliminacji drgań pozostaje niezmien-

Wplyw temperatury na obszar głównego rezonansu parametiycznego oscylatora i wahadła, przedstawiono na rysunkach 9 i 10.

Rys. 7 oraz rys. 8 przedstawiają przykładowe krzywe rezonansowe oscylatora i wahadła przy różnych wartościach tłumienia MR. Ciągła linia oznacza rozwiązanie stabilne, natomiast linia przerywana - niestabilne. Litery na wykresach przedstawiają charakterystyczne punkty wykryte za pomocą metody kontynuacji (L -punkt limitu, D - podwojenie rozwiązania, B -punkt bifurkacyjny). Analizując uzyskane wyniki, stwierdzono, że najkorzystniejszy obszar z punktu widzenia absorpcji

Zwiększenie temperatury 6. powoduje zmniejszenie amplitudy drgań oraz przegięcie krzywych rezonansowych oscylatora w prawą stronę. Ciekawym zaobserwowanym wynikiem wydaje się być redukcja charakterystycznego przegięcia krzywej rezonansowej (czarna linia na rys. 9). Zjawisko to, występuje w układzie z klasyczną sprężyną, i świadczy o tym, że w pewnym zakresie ruch w-ahadła może wzbudzić większe drgania oscylatora, niż drgania bez zastosowanego eliminatora. Podobny