834706959

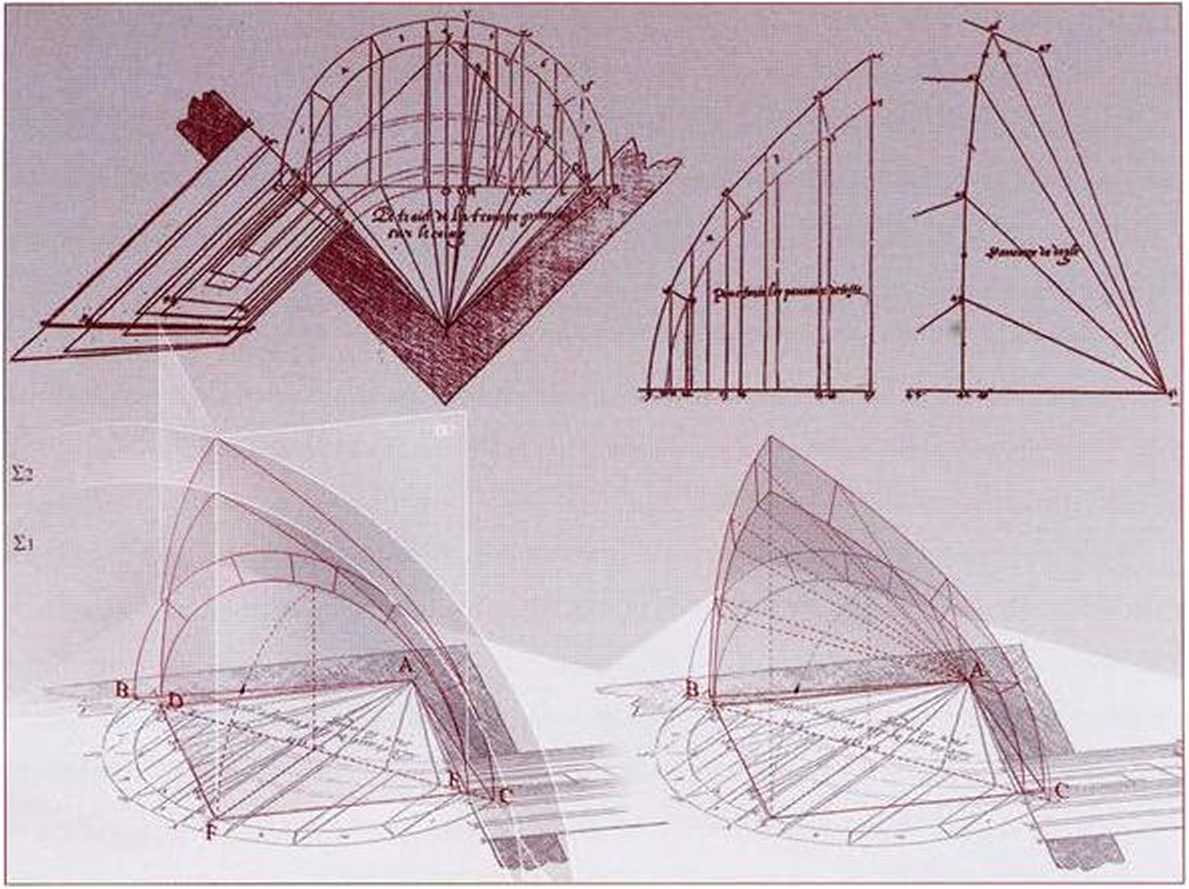
2 - Trait di de rOrnte relatiuo ad una Trompe quadrata e ricostruzione delle geometrie di base della Trompe

⁷    Cfr. Philibert de 1'Orme, op. cit.,

p. 101.

⁸    fc evidentc, quindi, come le geometrie delle trompes varino rispetto a due parametri: il profilo della di-rettrice della superficie conica che la origina e il profilo della direttrice di una qualsiasi superficie rigata verti-cale che la seziona, le cui reciproche variazioni sono alPorigine di formę diverse della stessa tipologia.

⁹    In qucsto caso la superficie ci-lindrica di taglio si riduce a due piani verticali.

^ł0 Nella partizione delParco circolare, sezione retta della trompe, i conci sono tutti diversi. Questo si verifica perchć la testa dei conci non apparticne a questo arco ma ai piani di taglio della trompe.

30

ra, quello dedicato ad una trompe quadrata⁷ (fig. 2).

La genesi geometrica di una trompe si determina immaginando la superficie di un generico cono avente per direttrice un profilo qualsiasi orientata in maniera tale da avere due generatrici disposte secondo le imposte della volta. Sezionando la superficie conica eon una superficie cilindrica a direttrice generica o eon alcuni piani, si ottiene la superficie di intradosso di una trompe^H.

Nel trait redatto da de 1'Orme & visibile la sezione, campita, dei muri su cui poggera la trompe. II profilo circolare su cui £ indicata la partizione dei conci non & altro che la direttrice circolare del cono ribaltata sul piano d'imposta della vol-ta; sempre sul piano orizzontale si trovano le proiezioni delle superfici verticali di taglio⁹. Stabilite le geometrie di base, il problema da risolvere consiste nel determinare il numero dei conci per poter ricavare poi la vera grandezza delle superfici di cui ognuno si compone. La scelta del numero di conci da ottenere & indicata sul profilo della direttrice del cono ribaltato sul piano orizzontale: in questo caso de 1'Orme propone una suddivisione in sette elementi¹⁰. Una volta stabilito il numero e la dimensione dei conci che dovranno formare la volta, si procede alla determinazione delle superfici che li compongono. Ogni concio & costituito da cinque superfici diverse fra loro (ad eccezione di quello in chiave che ne conta sei). Per ricostruire la vera forma delle superfici di ogni concio, ba-stera determinare la posizione reciproca dei vertici dei poligoni che le definisco-no. Tutte le informazioni necessarie alla soluzione del problema sono contenute nella sezione retta della trompe; infatti, dopo la prima operazione di ribaltamento del piano della sezione retta, si ruotano e si ribaltano i piani proiettanti le ge-

Marta Salvatore