8812710991

W celu ułatwienia zastosowania czujników tensometrycznych w praktyce, powyższe wyrażenia należałoby sprowadzić do postaci, w której możliwe byłoby stosowanie wielkości fizycznych mierzalnych w prosty sposób. W zawiązku z tym na podstawie powyższych wyrażeń można wyznaczyć wartość określającą właściwości tensometru oporowego, zwaną współczynnikiem czułości odkształceniowej k oraz powiązać go z wielkościami takimi jak rezystancja i odkształcenie. Należy podkreślić, iż stała tensometru podawana jest przez wytwórcę, który wyrywkowo wyznacza ją dla produkowanej serii. Stała ta obowiązuje dla przypadku, gdy oś tensometru pokrywa się z kierunkiem odkształceń mierzonych, a wartość względnych zmian rezystancji tensometrów drutowych przyjmuje ułamki procent przy maksymalnym odkształceniu układu.

Dalszą analizę przejścia do uzyskania współczynnika czułości odkształceniowej można przedstawić następująco.

Po zlogarytmowaniu wyrażenia (1) otrzymujemy równanie (4):

lnR = ln_/o + lnl-ln A    (4)

które następnie różniczkujemy, wynikiem czego jest równanie (5):

AR _ Ap ^ Al AA R ~ p 1 A

Następnie przy przejściu do przyrostów skończonych, otrzymamy równanie (6): dR d p dl dA R    p    1    A

Wprowadzając liczbę Poissona ju dla danego materiału drutu oporowego o średnicy d otrzymujemy zależność:

Ad

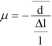
w której d jest średnicą drutu, a 1 długością przewodnika. Podstawiając do równania (7) pole przekroju drucika oporowego: oraz następnie przekształcone równanie (7) do równania określając z równania (4) otrzymamy zależność:

f = f(l _{+ 2/},)₊^    (9)

R 1    p

Następnie z równania (7) można wyodrębnić poszukiwany współczynnik czułości odkształceniowej k, który jest ilorazem względnego przyrostu rezystancji oraz wydłużenia jednostkowego:

4