
1
4. Kinematyka odwrotna
Zadanie kinematyki odwrotnej jest przeciwieństwem zadania kinematyki prostej;
można opisać je następująco: mając daną pozycję i orientację końcówki technologicznej,
wyznacz zmienne złączowe, które zapewniają osiągnięcie docelowej pozycji i orientacji. W
ogólnym przypadku jest to zadanie trudniejsze, niż zadanie kinematyki prostej, ponieważ na
ogół nie istnieje jednoznaczne rozwiązanie nieliniowych równań kinematyki.
Problem kinematyki odwrotnej można przedstawić następująco: dana jest jednorodna
macierz przekształcenia 4x4
=
=
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
1
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
0
p
R
H
,
należy znaleźć jedno lub wszystkie rozwiązania równania
H
H
=
)
,
,
,
(
2
1
0
n
n
q
q
q
K
(1)
gdzie:
=
=
−
44
43
42
41
34
33
32
31
24
23
22
21
14
13
12
11
1
2
2
1
1
1
0
2
1
0
)
(
)
(
)
(
)
,
,
,
(
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
q
q
q
q
q
q
n
n
n
n
n
H
H
H
H
K
K
Równanie (1) daje 12 równań z n niewiadomymi, które można zapisać jako
4
,
3
,
2
,
1
;
3
,
2
,
1
;
)
,
,
,
(
2
1
=
=
=
j
i
h
q
q
q
H
ij
n
ij
K
gdzie:
ij
ij
h
H ,
oznaczają 12 nietrywialnych elementów macierzy, odpowiednio
n
H
0
i H .
Ponieważ ostatni wiersz obu macierzy jest równy (0,0,0,1), więc spośród 16 równań
reprezentowanych przez zależność (1) cztery są trywialne.
Zadanie odwrotne kinematyki można próbować rozwiązać na wiele sposobów np.
wykorzystując podejście geometrycznie, analitycznie lub numerycznie.
4.1. Podejście geometryczne
4.1.1. Manipulator płaski z łokciem
Dla manipulatora płaskiego z łokciem (rys. 1) zadanie odwrotne kinematyki polega na
znalezieniu zmiennych złączowych
θ
1
i
θ
2
dla znanych długości członów manipulatora
odpowiednio a
1
i a
2
oraz danego położenia chwytaka (x, y).
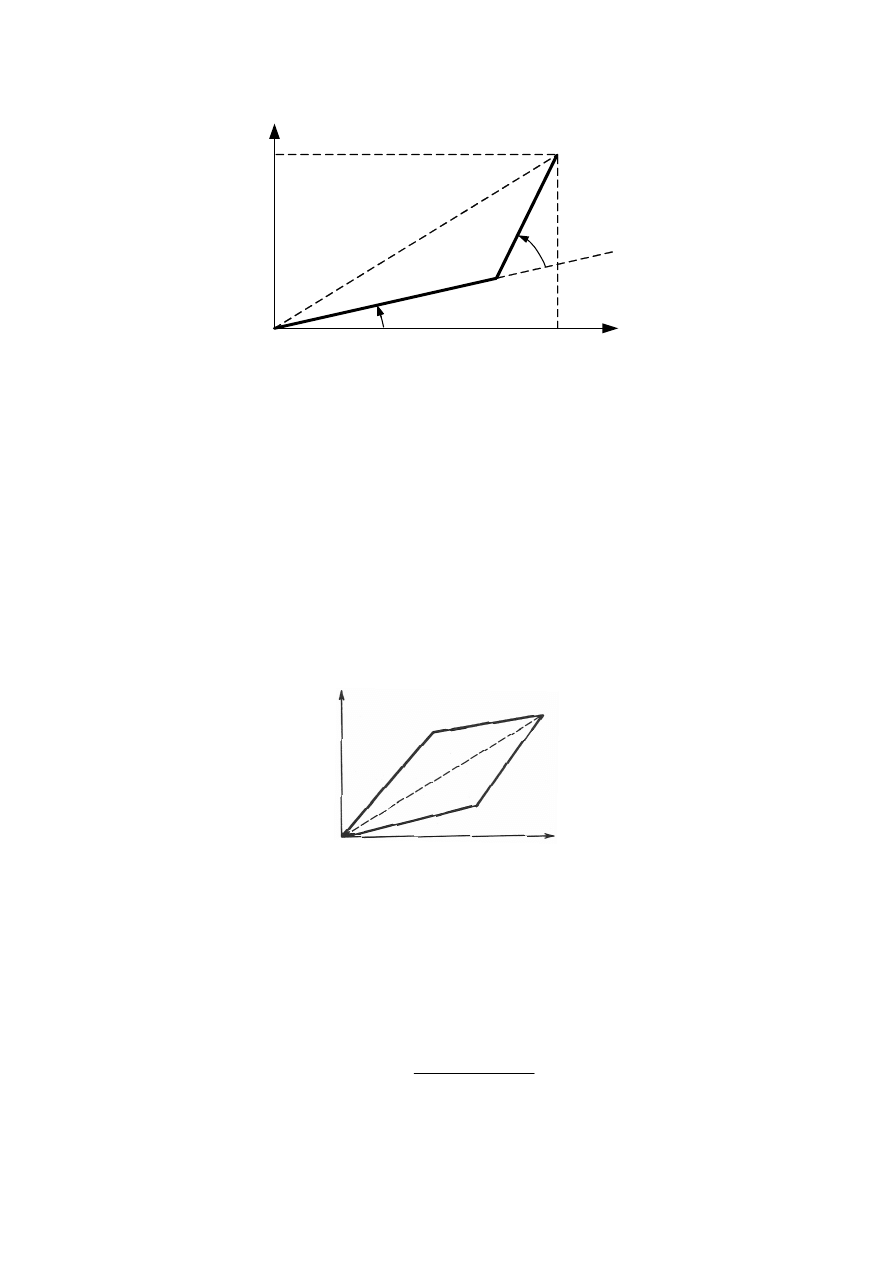
2
Rys. 1. Wyznaczenie kątów w złączach dwuczłonowego manipulatora płaskiego z łokciem
Ponieważ równania kinematyki prostej są najczęściej nieliniowe, przez co znalezienie
rozwiązania kinematyki odwrotnej może nie być łatwe i w ogólności nie będzie to
rozwiązanie jednoznaczne. Na przykład dla rozważanego przypadku nie ma rozwiązania gdy
dane współrzędne (x,y) są poza zasięgiem manipulatora. Istnieje jedno rozwiązanie, gdy
ramiona są całkowicie wyprostowane. Gdy współrzędne (x,y) mieszczą się w zasięgu
manipulatora, mogą istnieć dwa rozwiązania (rys. 2), czyli konfiguracje „łokieć u góry” i
„łokieć u dołu”.
Rys. 2. Rozwiązanie niejednoznaczne kinematyki odwrotnej
Stosując prawo cosinusów, można wyznaczyć kąt
θ
2
w następujący sposób:
)
180
cos(
2
)
(
2
2
1
2
2
2
1
2
2
θ
−
−
+
=
+
o
a
a
a
a
y
x
)
cos(
)
180
cos(
2
2
θ
θ
−
=
−
o
D
a
a
a
a
y
x
=
−
−
+
=
:
2
)
cos(
2
1
2
2
2
1
2
2
2
θ
(2)
D
arccos
2
=
θ
θ
1
θ
2
a
1
a
2
y
x
łokieć u góry
łokieć u dołu
3
Jednakże lepszym sposobem znalezienia kąta
θ
2
jest zauważenie, że jeśli cos
θ
2
jest dany
wzorem (2), to sin
θ
2
jest dany odpowiednio wzorem
2
2
1
sin
D
−
±
=
θ
stąd
−
±
=
D
D
2
2
1
arctan
θ
(3)
Zaletą tego podejścia jest rozróżnienie obu konfiguracji „łokieć u góry” i „łokieć u dołu”
przez wybór odpowiedniego znaku w równaniu (3). Kąt
θ
1
można wyznaczyć w następujący
sposób:
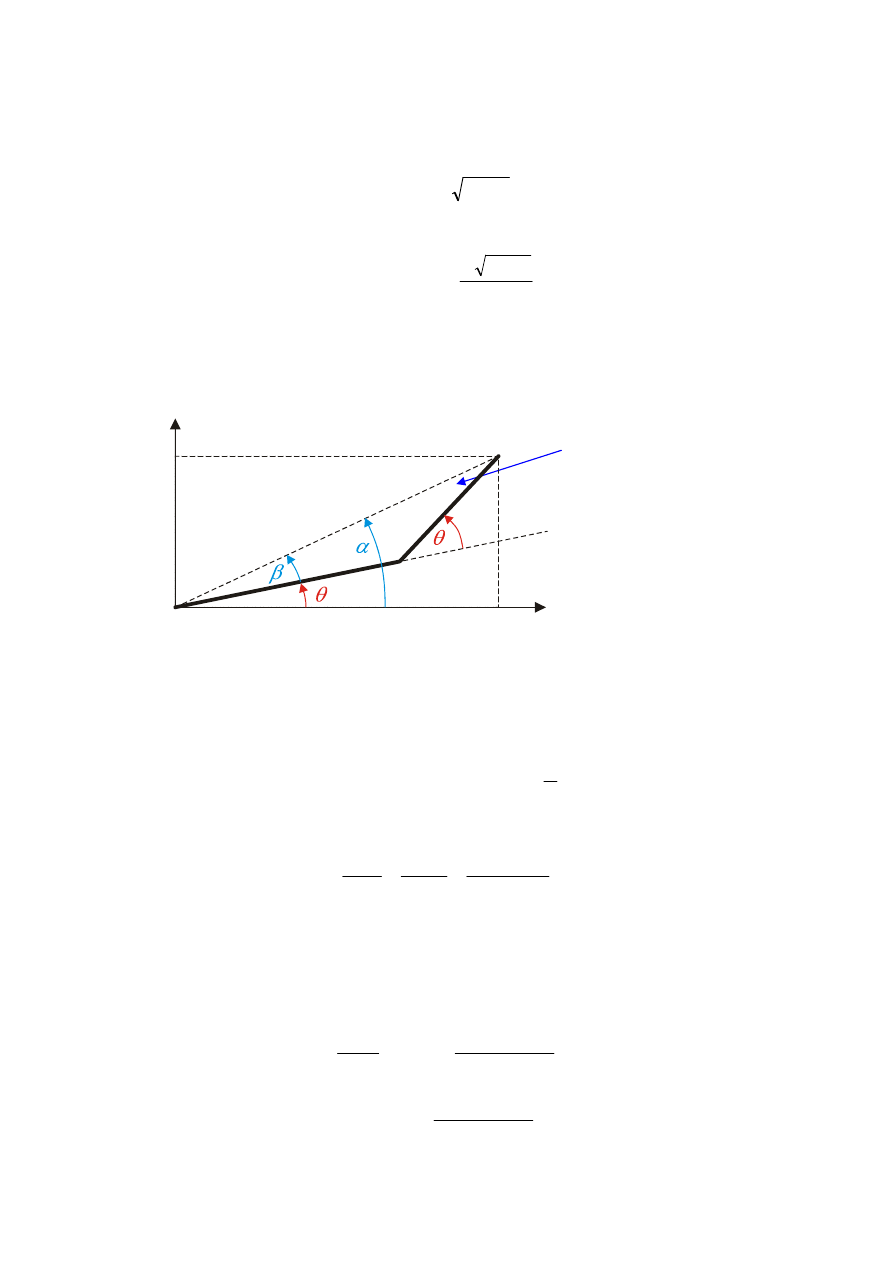
Rys. 3. Manipulator płaski z łokciem – wyznaczenie kąta
θ
1
Na podstawie rys. 3 można napisać:
β
α
θ
−
=
1
gdzie:
=
x
y
arctan
α
Stosując prawo sinusów można wyznaczyć kąt β według wzorów
1
2
1
2
)
sin(
)
sin(
sin
a
a
a
β
θ
γ
β
−
=
=
β
θ
β
θ
β
θ
sin
cos
cos
sin
)
sin(
2
2
2
−
=
−
β
θ
β
θ
β
sin
cos
cos
sin
sin
2
2
2
2
1
a
a
a
−
=
β
θ
θ
β
cos
sin
)
cos
(
sin
2
2
2
2
1
a
a
a
=
+
2
2
1
2
2
cos
sin
tan
cos
sin
θ
θ
β
β
β
a
a
a
+
=
=
+
=
2
2
1
2
2
cos
sin
arctan
θ
θ
β
a
a
a
β
θ
γ
θ
γ
β
θ
γ
β
γ
−
=
⇒
=
+
=
−
+
+
2
2
2
180
180
o
o
y
x
a
2
1
a
1
2
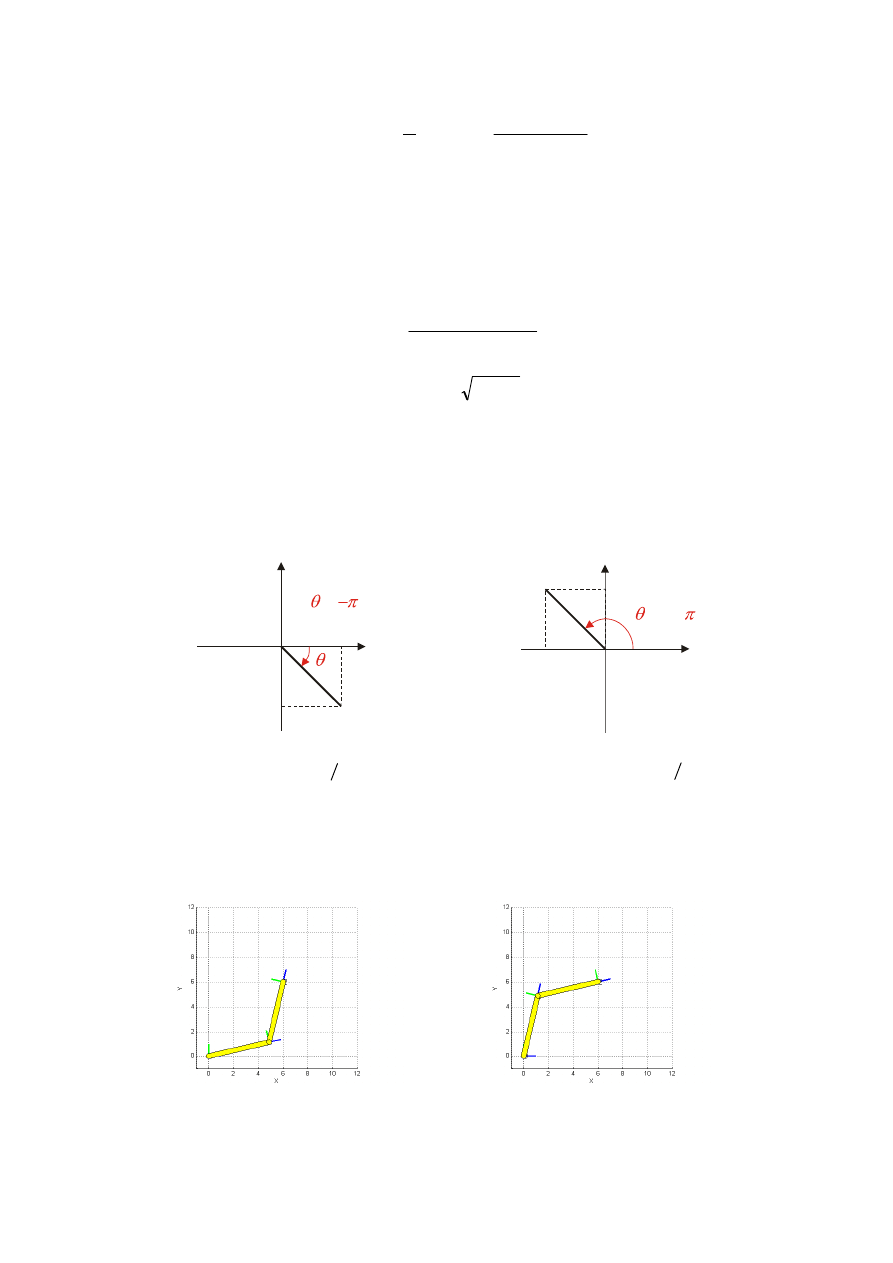
4
+
−
=
2
2
1
2
2
1
cos
sin
arctan
arctan
θ
θ
θ
a
a
a
x
y
(4)
Zauważmy, że kąt
θ
1
zależy od kąta
θ
2
. Ma to znaczenie fizyczne, gdyż oczekujemy różnych
wartości kąta
θ
1
w zależności od tego, które rozwiązanie wybierzemy dla kąta
θ
2
.
Zatem, zmienne złączowe manipulatora płaskiego z łokciem można wyznaczyć przy użyciu
następującego algorytmu:
2
1
2
2
2
1
2
2
2 a
a
a
a
y
x
D
−
−
+
=
(5a)
−
±
=
D
D ,
1
atan2
2
2
θ
(5b)
( )
(
)
2
2
1
2
2
1
cos
,
sin
atan2
,
atan2
θ
θ
θ
a
a
a
x
y
+
−
=
(5c)
gdzie atan2(y,x) jest dwuargumentową funkcją obliczającą wartość arctan(y/x) z
uwzględnieniem znaków zarówno przy x jak i y, w celu znalezienia ćwiartki, w której leży
szukany kąt. Na przykład:
Na rys. 4 przedstawiono rozwiązania odwrotnego zadania kinematyki manipulatora płaskiego
o wymiarach a
1
= 5, a
2
= 5 i pozycji zadanej x = 6, y = 6 dla konfiguracji „łokieć u dołu” (rys.
4a) i „łokieć u góry” (rys. 4b). Obliczenia wykonano w programie Matlab.
Rys. 4. Rozwiązanie odwrotnego zadania kinematyki dla manipulatora płaskiego z łokciem
4
)
1
,
1
(
atan2
π
−
=
−
4
3
)
1
,
1
(
atan2
π
+
=
−
Y
X
1
-1
= /4
Y
X
1
-1
= +3 /4
th2= atan2(sqrt(1-D^2),D);
th1 = 13.0519°
th2 = 63.8961°
th2= atan2(-sqrt(1-D^2),D);
th1 = 76.9481°
th2 = -63.8961°
a)
b)
5
4.1.2. Manipulator z łokciem (manipulator stawowy)
Schemat kinematyczny manipulatora stawowego z przyporządkowanymi do niego
układami współrzędnych przedstawiono na rys. 5.
Rys. 5. Schemat kinematyczny manipulatora stawowego.
Rzutując wektor
p
O
na płaszczyznę
0
X
0
Y zmienną złączową
θ
1
można wyznaczyć z równania:
)
,
(
atan2
1
Ox
Oy
p
p
=
θ
W celu znalezienia kątów
θ
2
i
θ
3
rozważamy płaszczyznę utworzoną przez ogniwa 2 i 3.
Ponieważ ruchy tych członów są płaskie, dalsze rozważania są identyczne jak dla
manipulatora płaskiego z łokciem. Na podstawie (5) można napisać:
(6a)
−
±
=
,D
D
2
3
1
atan2
θ
(6b)
( )
(
)
=
+
−
=
,
cos
,
sin
atan2
,
atan2
3
3
2
3
3
2
θ
θ
θ
a
a
a
r
s
O
(
)
,
cos
,
sin
atan2
,
atan2
3
3
2
3
3
2
2
1
θ
θ
ε
a
a
a
p
p
p
Oy
Ox
Oz
+
−
+
−
=
(6c)
0
X
0
Y
0
Z
1
Z
2
Z
1
X
p
O
p
Oy
p = s+
Oz
1
p
Ox
s
1
1
r
O
s
0
Z
r
O
a
2
a
3
θ
3
θ
2
s
0
Z
r
O
a
2
a
3
θ
3
θ
2
(
)
3
2
2
3
2
2
2
1
2
2
3
2
2
3
2
2
2
2
2
2
a
a
a
a
p
p
p
a
a
a
a
s
r
D
Oz
Oy
Ox
O
−
−
−
+
+
=
−
−
+
=
ε
6
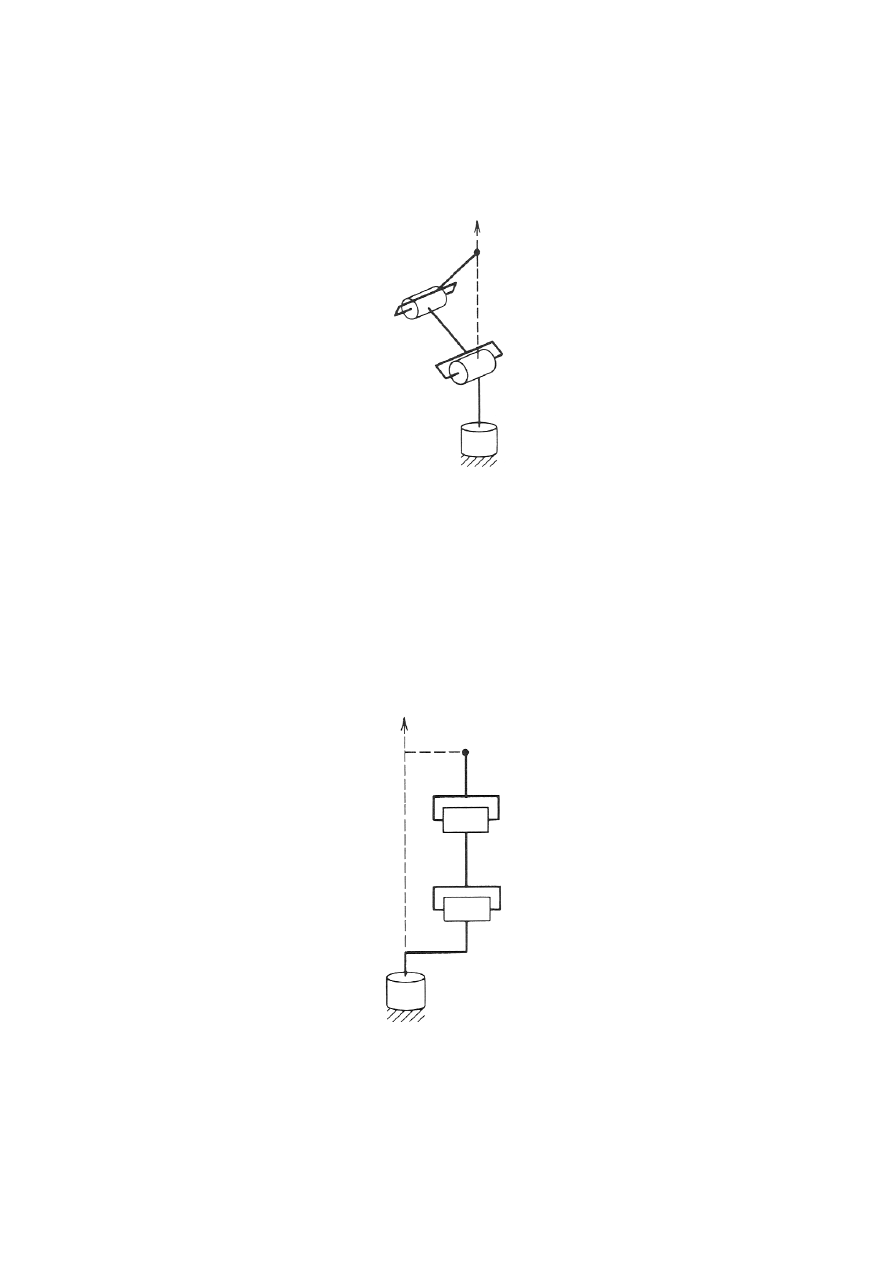
Gdy
p
Ox
= p
Oy
= 0 równanie
)
,
(
atan2
1
Ox
Oy
p
p
=
θ
jest nieokreślone, a manipulator znajduje
się w pozycji osobliwej (rys. 6).
0
Z
Rys. 6. Konfiguracja osobliwa manipulatora stawowego
W tej pozycji efektor (opisany wektorem
p
O
) leży na osi
0
Z. Dla każdej wartości kąta
θ
1
położenie efektora jest stałe, tzn. istnieje nieskończenie wiele rozwiązań dla
θ
1
.
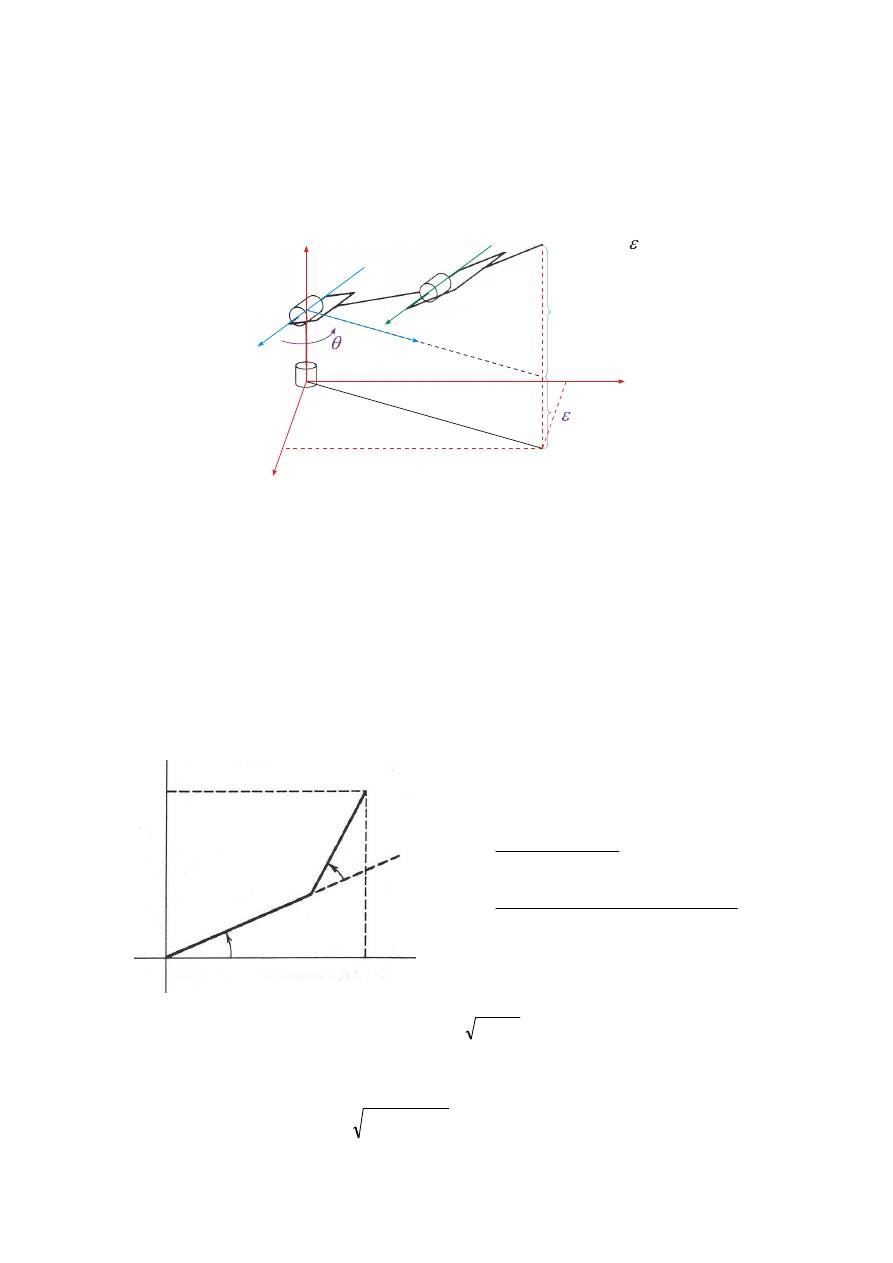
Jeżeli dla rozważanego manipulatora wprowadzi się przesunięcie
a
1
≠ 0 (rys. 7), wówczas
ś
rodek kiści nie może leżeć na osi
0
Z.
0
Z
a
1
Rys. 7. Manipulator z łokciem i przesuniętym barkiem
W tym przypadku istnieją dwa rozwiązania dla kąta
θ
1
, tzw. konfiguracja lewego i prawego
ramienia.
7
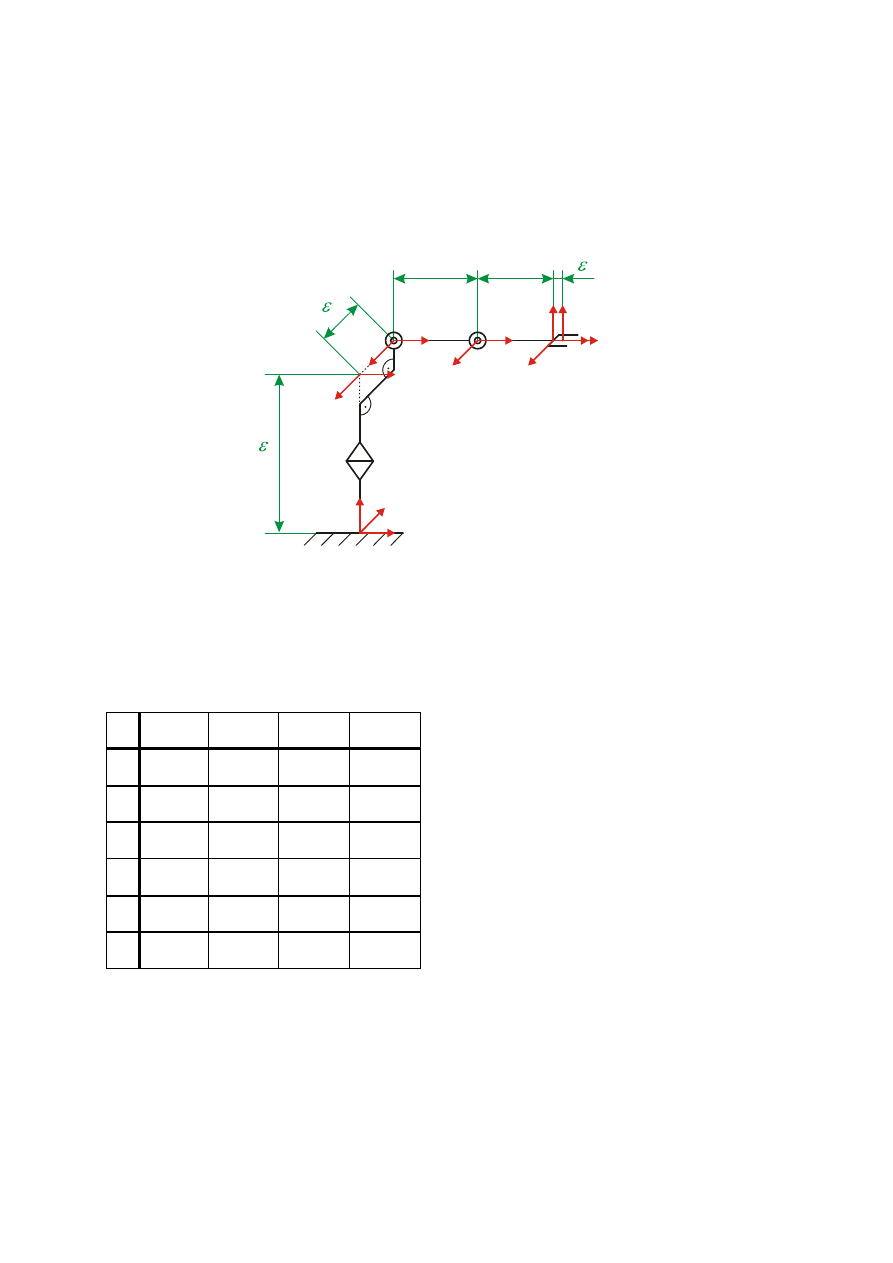
4.1.3. Manipulator z łokciem (stawowy) i przesuniętym barkiem
Schemat kinematyczny manipulatora stawowego z przesuniętym barkiem wraz z
przyporządkowanymi do niego układami współrzędnych, zgodnie z reprezentacją D-H,
przedstawiono na rys. 8.
Rys. 8. Schemat kinematyczny manipulatora z łokciem i przesuniętym barkiem
W tab. 1 zamieszczono parametry D-H rozważanego manipulatora.
Tab. 1. Parametry D-H manipulatora stawowego z przesuniętym barkiem
θ
i
ε
i
a
i
α
i
1
θ
1
*
ε
1
0
+90
°
2
0
−
ε
2
0
0
3
θ
3
*
0
a
3
0
4
θ
4
*
0
a
4
0
5
+90
°
0
0
+90
°
6
0
ε
6
0
0
Rozważmy konfigurację lewego i prawego ramienia.
0
Z
a
3
6
2
1
a
4
0
X
0
Y
1
X
2
X
3
X
5
X
6
X
4
X,
1
Z
2
Z
3
Z
4
Z
5
Z,
6
Z
8
Konfiguracja lewego ramienia - na podstawie (6) można napisać
(
)
(
)
(
)
(
)
6
4
3
2
6
4
2
3
2
1
2
2
2
2
2
ε
ε
ε
ε
+
+
−
−
−
+
−
+
=
a
a
a
a
p
p
p
D
Oz
Oy
Ox
−
±
=
D
D ,
1
atan2
2
4
θ
(
)
(
)
(
)
4
6
4
3
4
6
4
2
2
2
2
1
3
cos
,
sin
atan2
,
atan2
θ
ε
θ
ε
ε
ε
θ
+
+
+
−
−
+
−
=
a
a
a
p
p
p
Oy
Ox
Oz
Konfiguracja prawego ramienia - wyznacz
θ
4
i
θ
3
jak dla konfiguracji lewego ramienia i
zmień je w następujący sposób
4
4
-
θ
θ
=
3
3
-
180
θ
θ
°
=
Konfiguracja lewego ramienia
Konfiguracja prawego ramienia
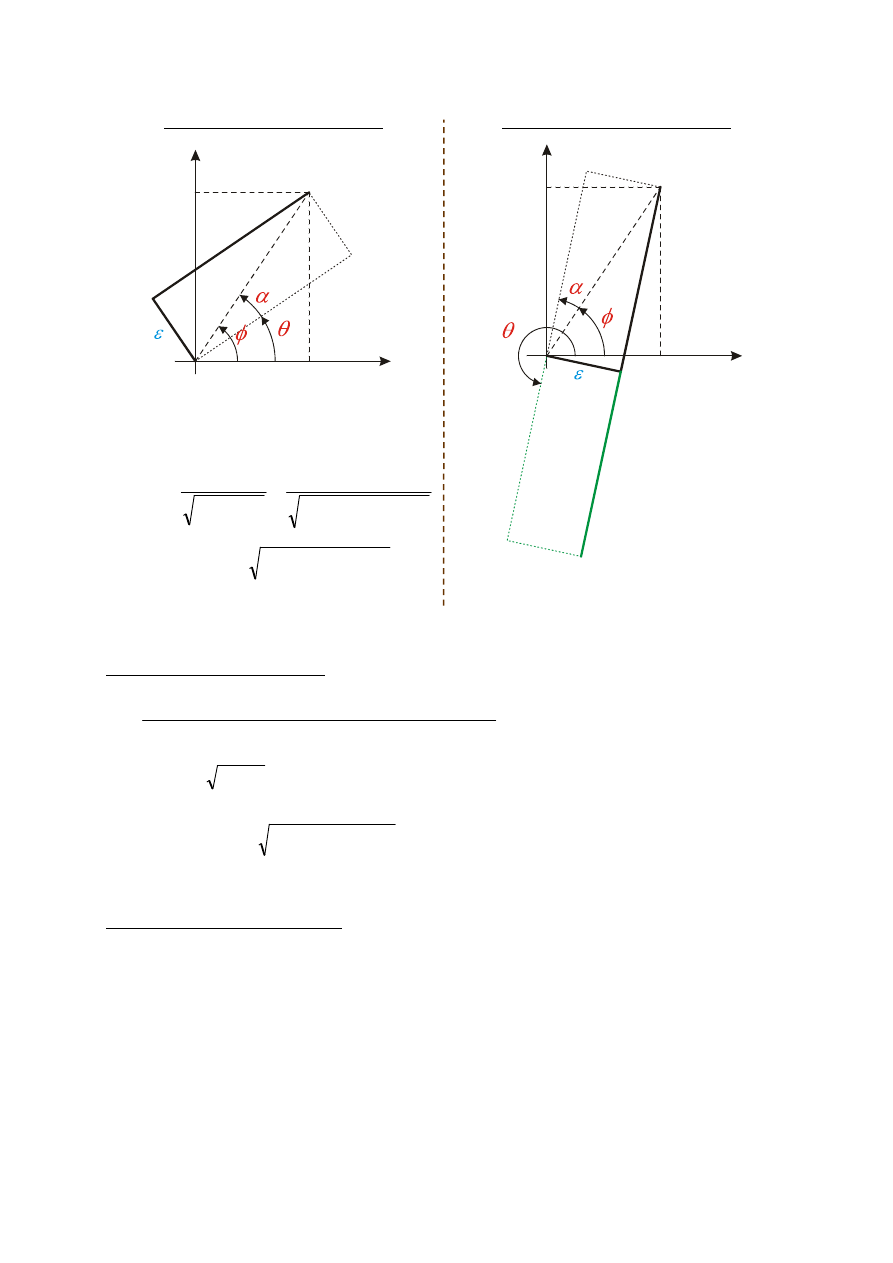
Z rysunku widzimy że:
α
φ
θ
−
=
1
)
,
(
atan2
Ox
Oy
p
p
=
φ
gdzie:
2
2
2
2
2
2
2
2
2
)
tan(
ε
ε
ε
ε
α
−
+
=
−
=
Oy
Ox
O
p
p
r
−
+
=
2
2
2
2
2
,
atan2
ε
ε
α
Oy
Ox
p
p
0
X
p
Ox
p
Oy
r
O
0
Y
2
1
0
X
p
Ox
p
Oy
r
O
0
Y
2
1
Z rysunku widzimy że:
°
+
+
=
180
1
α
φ
θ
9
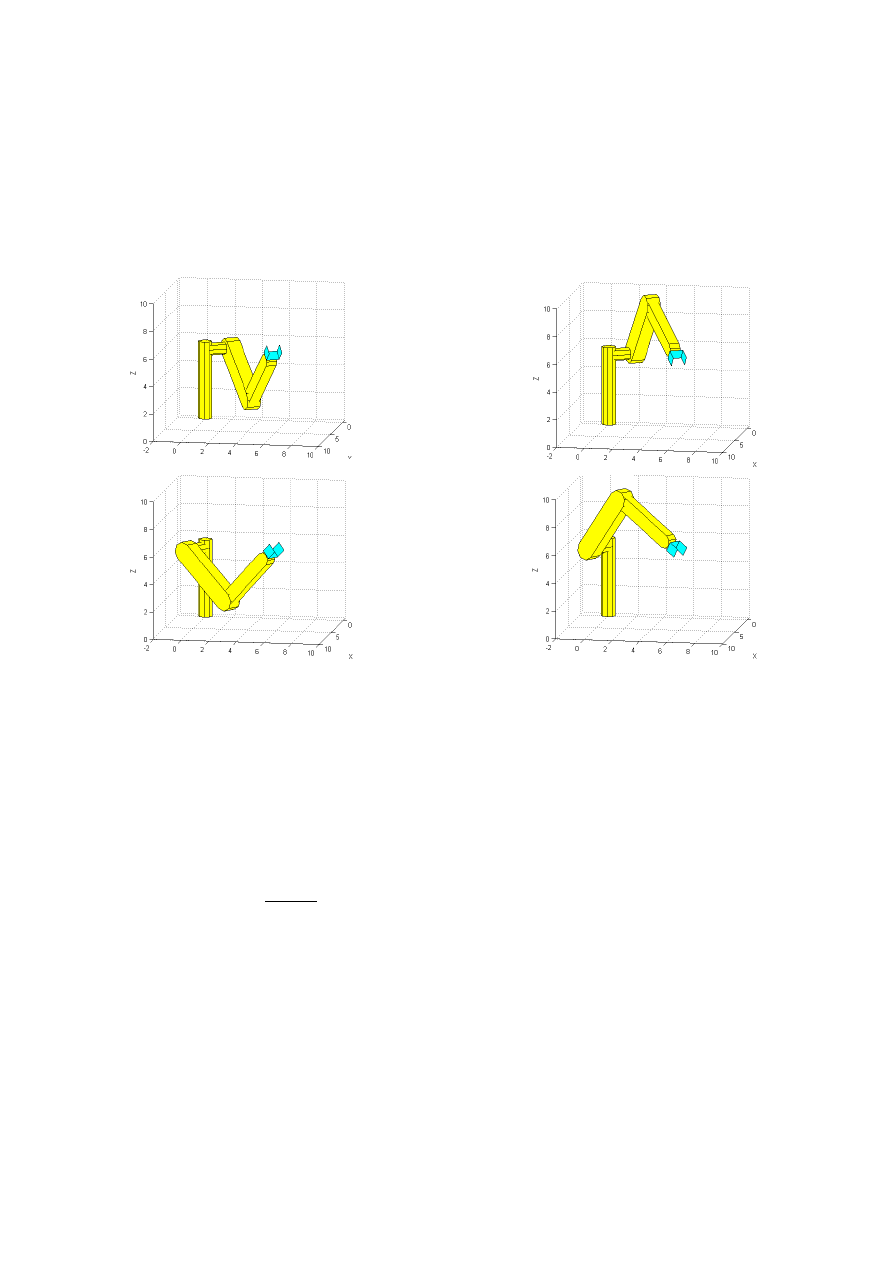
Przykładem manipulatora z łokciem i przesunięciem w barku jest robot PUMA. Dla tego
robota możliwe są cztery rozwiązania zadania kinematyki odwrotnej: a) ramię z lewej strony
u dołu (rys. 9a), b) ramię z lewej strony u góry (rys. 9b), c) ramię z prawej strony u dołu (rys.
9c), d) ramię z prawej strony u góry (rys. 9d).
Rys. 9. Rozwiązanie odwrotnego zadania kinematyki dla manipulatora PUMA.
Zmienne złączowe wyznaczono dla p
Ox
= p
Oy
= p
Oz
= 6.
Wymiary manipulatora:
ε
1
=5;
ε
2
=2; a
3
=5; a
4
=5;
ε
6
=1.
4.2. Odsprzężenie kinematyczne
Zadanie odwrotne kinematyki jest raczej problemem trudnym, jednak okazuje się, że
dla manipulatorów o sześciu stopniach swobody, których ostatnie trzy osie przecinają się w
jednym punkcie, jest możliwe
odsprzężenie powodujące podział kinematyki odwrotnej na
dwa prostsze zadania, nazwane kinematyką odwrotną pozycji i kinematyką odwrotną
orientacji. Pierwsze polega na znalezieniu punktu przecięcia osi kiści (zwanego środkiem
kiści) drugie na znalezieniu orientacji kiści. Przedstawmy zależność (1) dla manipulatora o
sześciu stopniach swobody w następującej postaci
°
=
°
=
°
=
-82.3377
52.6286
31.3670
4
3
1
θ
θ
θ
°
=
°
=
°
=
82.3377
-38.7998
31.3670
4
3
1
θ
θ
θ
°
=
°
=
°
=
-82.3377
218.7998
238.6330
4
3
1
θ
θ
θ
°
=
°
=
°
=
82.3377
127.3714
238.6330
4
3
1
θ
θ
θ
a)
b)
c)
d)
10
p
p
R
R
=
=
)
,
,
(
)
,
,
(
6
1
6
,
0
0
6
1
6
0
q
q
q
q
K
K
gdzie: p i R opisują odpowiednio daną pozycję i orientację układu narzędzia (układu {6},
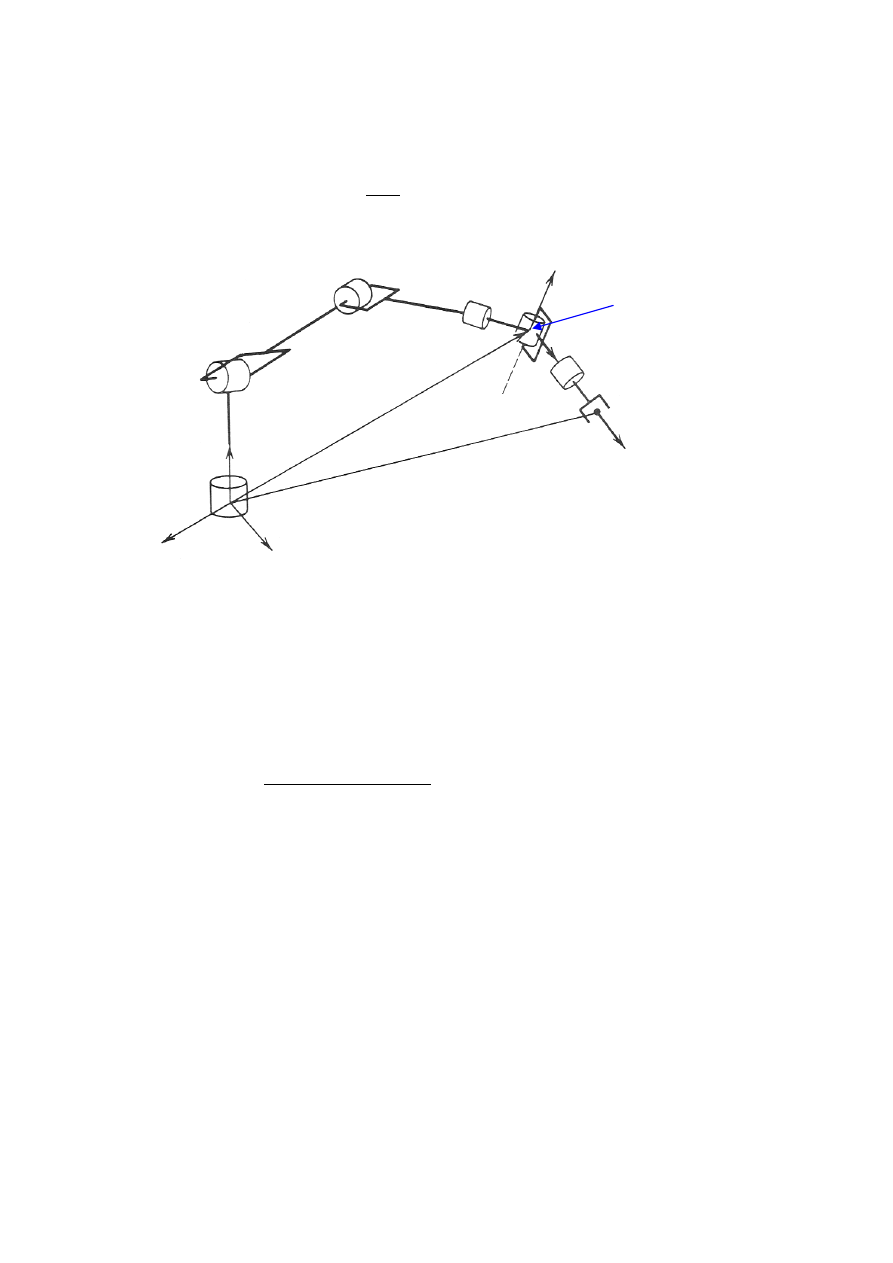
patrz rys. 10).
Rys. 10. Odsprzężenie kinematyczne
Dla rozważanej kiści osie
4
Z,
5
Z,
6
Z przecinają się w punkcie O, stąd początki układów {4} i
{5} umieszczonych zgodnie z konwencją D-H będą zawsze w środku kiści - punkt O. Często
początek {3} będzie również w O, ale nie jest to konieczne do dalszych rozważań.
Ważnym punktem przedstawionego założenia dla kinematyki odwrotnej jest to, że ruch
ostatnich trzech osi nie zmienia położenia punktu O. Zatem położenie środka kiści jest
funkcją tylko pierwszych trzech zmiennych złączowych q
1
, q
2
, q
3
.
0
p
O
oznacza wektor od
początku układu bazowego do środka kiści. Układ współrzędnych końcówki roboczej ({6}),
względem układu bazowego, opisany jest przez wektor p i orientację R = (r
ij
). Ponieważ
początek układu {6} jest przesunięty o odległość
6
ε
wzdłuż osi
5
Z od punktu O można
napisać
k
R
p
p
6
0
ε
−
=
O
(7)
Jeżeli współrzędne wektora p oznaczymy przez p
x
, p
y
, p
z
a współrzędne wektora środka kiści
przez p
Ox
, p
Oy
, p
Oz
to równanie (7) przyjmuje postać:
−
−
−
=
33
6
23
6
13
6
r
p
r
p
r
p
p
p
p
z
y
x
Oz
Oy
Ox
ε
ε
ε
(8)
0
p
O
p
0
X
0
Y
0
Z
4
Z
5
Z
6
Z
ś
rodek kiści - punkt O
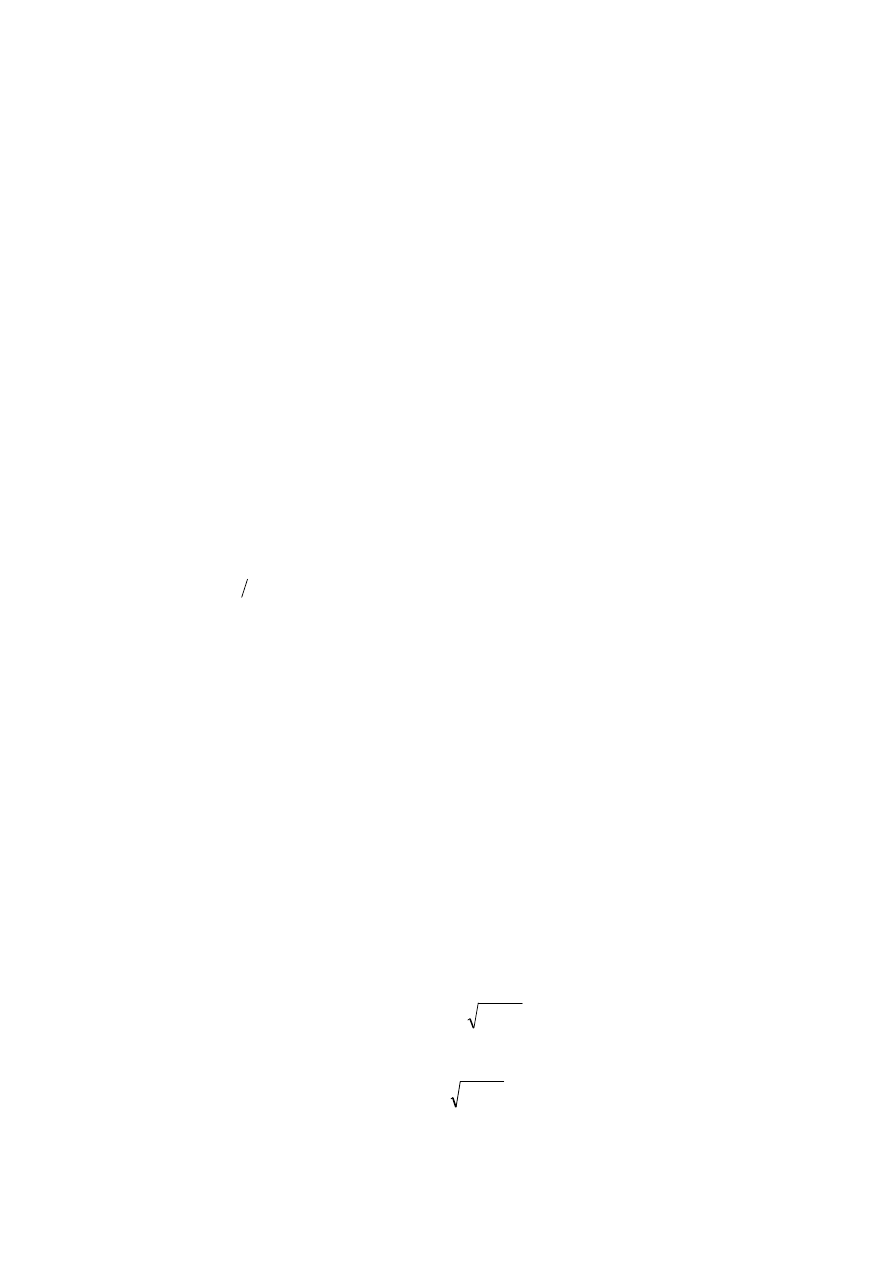
11
Znając położenie środka kiści (8) można wyznaczyć wartości pierwszych trzech zmiennych
złączowych q
1
, q
2
, q
3
stosując podejście geometryczne. Na podstawie wyznaczonych
pierwszych trzech zmiennych złączowych należy obliczyć macierz obrotu
3
0
R która zależy
tylko od tych wielkości. Następnie z wyrażenia
6
3
3
0
R
R
R
=
(9)
można określić orientację końcówki roboczej (ostatnie trzy zmienne złączowe) względem
układu {3} jako
( )
( )
R
R
R
R
R
T
3
0
1
3
0
6
3
=
=
−
(10)
To, że konstrukcje manipulatorów rozwinęły się do takiego, a nie innego stanu
obecnego, spowodowane było częściowo trudnościami z odwrotnym zadaniem kinematyki.
Ogólnie można powiedzieć, że stopień skomplikowania zadania kinematyki odwrotnej
wzrasta ze wzrostem liczby niezerowych parametrów kinematycznych. Dla większości
manipulatorów wiele parametrów spośród
i
i
a
ε
,
jest równych zeru, wartości parametrów
i
α
wynoszą 0 lub
2
π
±
itd.
4.3. Kinematyka odwrotna kiści – podejście analityczne
Załóżmy, że dana jest macierz U = (u
ij
)
3x3
, gdzie UU
T
= 1
, det(U)=1
oraz przekształcenie
3
R
6
kiści (patrz rozdział 3, str. 8 i 9). Zadaniem jest znalezienie kątów
θ
4
,
θ
5
,
θ
6
, spełniających równanie macierzowe
U
R
=
6
3
=
−
+
−
+
−
−
−
33
32
31
23
22
21
13
12
11
5
6
5
6
5
5
4
6
4
6
5
4
6
4
6
5
4
5
4
6
4
6
5
4
6
4
6
5
4
c
s
s
c
s
s
s
c
c
s
c
s
s
c
c
c
s
s
c
c
s
s
c
c
s
s
c
c
c
u
u
u
u
u
u
u
u
u
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
(11)
1) Jeśli u
13
i u
23
≠ 0 wówczas s
θ
5
≠ 0 i wtedy elementy u
31
i u
32
nie są jednocześnie
równe zeru. Ponieważ c
θ
5
= u
33
stąd
2
33
5
1
s
u
−
±
=
θ
, zatem
−
=
33
2
33
5
,
1
atan2
u
u
θ
lub

12
−
−
=
33
2
33
5
,
1
atan2
u
u
θ
Dla s
θ
5
>
0 otrzymujemy:
(
)
13
23
4
,
atan2
u
u
=
θ
(
)
31
32
6
,
atan2
u
u
−
=
θ
Dla s
θ
5
<
0 otrzymujemy:
(
)
13
23
4
,
atan2
u
u
−
−
=
θ
(
)
31
32
6
,
atan2
u
u
−
=
θ
2) Jeśli u
13
i u
23
= 0 (s
θ
5
=
0) wówczas u
33
= ±1 i u
31
= u
32
= 0. Dla tego przypadku
±
=
1
0
0
0
0
22
21
12
11
u
u
u
u
U
Dla u
33
=
1 → c
θ
5
= 1 i s
θ
5
= 0 więc
θ
5
= 0. W tym przypadku (11) przyjmuje postać:
=
+
+
+
−
+
=
+
−
+
−
−
−
1
0
0
0
0
1
0
0
0
)
c(
)
s(
0
)
s(
)
c(
1
0
0
0
c
c
s
s
s
c
c
s
0
c
s
s
c
s
s
c
c
22
21
12
11
6
4
6
4
6
4
6
4
6
4
6
4
6
4
6
4
6
4
6
4
6
4
6
4
u
u
u
u
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
Sumę
θ
4
+
θ
6
można wyznaczyć z:
(
)
(
)
11
,
12
11
21
6
4
atan2
,
atan2
u
u
u
u
−
=
=
+
θ
θ
(12)
Jeśli
θ
5
= 0 osie złącz 3 i 5 są współosiowe (rys. 11). Jest to konfiguracja osobliwa i
można wyznaczyć jedynie sumę
θ
4
+
θ
6
. Dla tego przypadku istnieje nieskończenie
wiele rozwiązań. Jednym z możliwych działań w takiej sytuacji jest wybranie dowolnej
wartości kąta
θ
4
i wyznaczenie
θ
6
z (12).
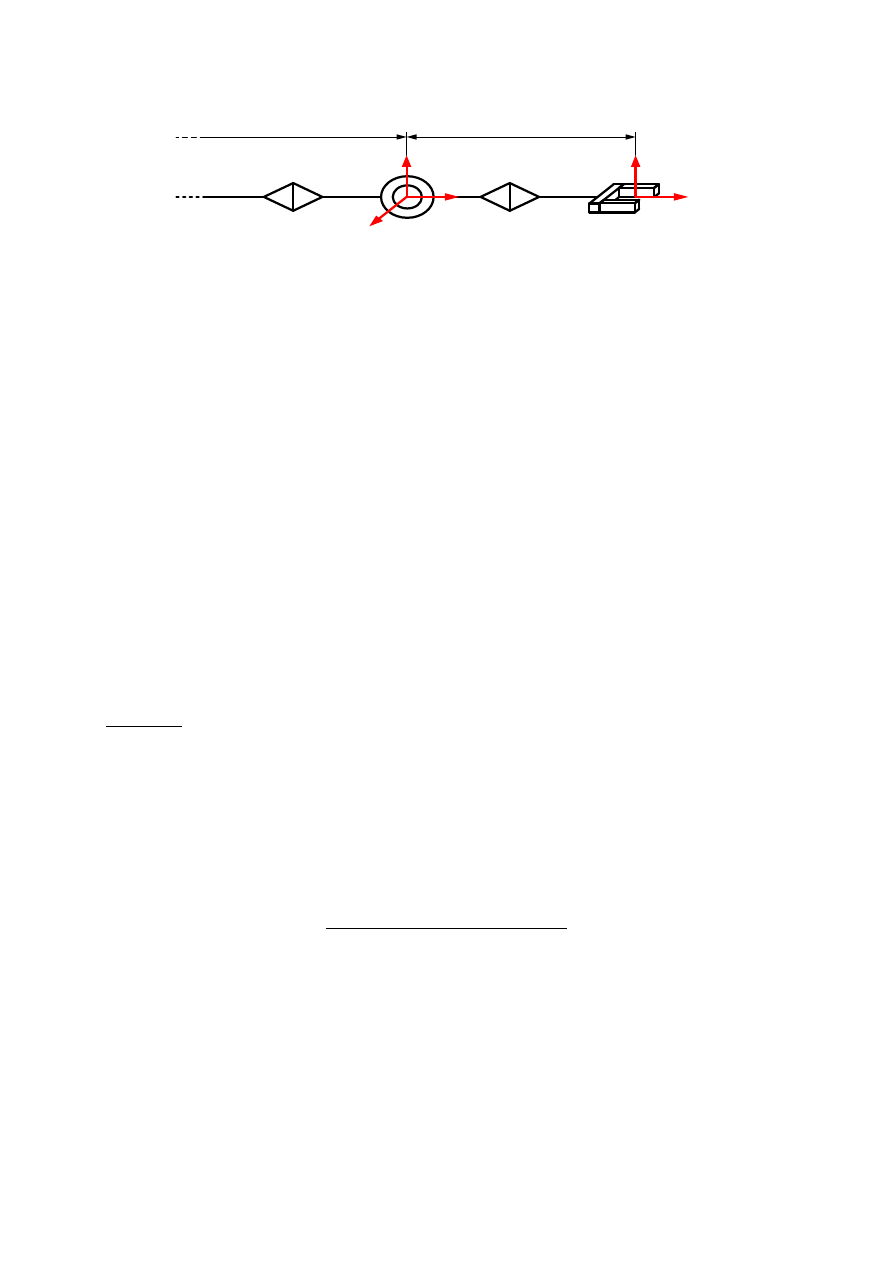
13
Rys. 11. Kiść sferyczna
Dla u
33
=
– 1 → c
θ
5
= – 1 i s
θ
5
= 0 więc
θ
5
=
π
. W tym przypadku (11) przyjmuje
postać:
−
=
−
−
−
−
−
−
−
1
0
0
0
0
1
0
0
0
)
c(
)
s(
0
)
s(
)
c(
22
21
12
11
6
4
6
4
6
4
6
4
u
u
u
u
θ
θ
θ
θ
θ
θ
θ
θ
Różnicę
θ
4
-
θ
6
można wyznaczyć z:
(
)
(
)
22
21
11
12
6
4
,
atan2
,
atan2
u
u
u
u
=
−
−
=
−
θ
θ
Również dla tego przypadku uzyskuje się nieskończenie wiele rozwiązań.
Literatura:
[1] Craig J. J.: Wprowadzenie do robotyki. Mechanika i sterowanie, Wydawnictwa
Naukowo-Techniczne, 1995
[2] Jezierski E.: Dynamika robotów, Wydawnictwa Naukowo-Techniczne, 2006
[3] Spong M. W., Vidyasagar M.: Dynamika i sterowanie robotów, Wydawnictwa
Naukowo-Techniczne, 1997
Informacja o prawach autorskich
O ile nie zaznaczono inaczej, rysunki i teksty pochodzą z pozycji podanych w literaturze.
Niniejsze opracowanie stanowi pomoc do wykładu „Podstawy Robotyki”.
X
6
Z
6
,
,
,
5
4
3
X
X
X
Z
Z
5
3
,
Z
4
6
ε
Wyszukiwarka
Podobne podstrony:
Kinematyka odwrotna
Kinematyka odwrotna, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów
wykład 5 +matlab, W SPR nr 03 04 Kinematyka Odwrotna
6 Kinematyka odwrotna
Kinematyka odwrotna id 235013 Nieznany
kinematyka odwrotna
Kinematyka odwrotna
odwrotna kinematyka manipulatoa
Odwrotne zadanie kinematyki
Wykł 1B wstępny i kinematyka
Wyklad 06 kinematyka MS
Wyklad 05 kinematyka MS
3 Rodzaje jednorodnych transformacji stosowanych w kinematy
więcej podobnych podstron