dr A. Czech
II. CHARAKTERYSTYKI LICZBOWE STRUKTURY ZBIOROWOŚCI
Parametry statystyczne – liczby służące do syntetycznego opisu struktury zbiorowości
statystycznej
Podział stosowanych miar:
1.
Położenia – służą do określenia wartości zmiennej, wokół której skupiają się
wszystkie pozostałe wartości cechy.
2.
Zmienności (rozproszenia, dyspersji) – służą do badania stopnia zróżnicowania
wartości cechy.
3.
Asymetrii – służą do badania kierunku i siły zróżnicowania wartości zmiennej.
4.
Koncentracji – służą do badania stopnia nierównomierności rozkładu ogólnej
sumy wartości zmiennej pomiędzy poszczególne jednostki zbiorowości lub do
analizy stopnia skupienia poszczególnych jednostek wokół średniej.
1.
Miary położenia
A.
Klasyczne
•
ś
rednia arytmetyczna,
•
geometryczna,
•
harmoniczna.
dr A. Czech
2
B.
Pozycyjne
•
modalna (dominanta, wartość najczęstsza),
•
kwantyle – kwartyl pierwszy, drugi (mediana), trzeci.
2.
Miary zmienności (rozproszenia, dyspersji)
A.
Klasyczne
•
wariancja,
•
odchylenie standardowe, przeciętne
•
klasyczny współczynnik zmienności.
B.
Pozycyjne
•
rozstęp
•
odchylenie ćwiartkowe,
•
pozycyjny współczynnik zmienności
3.
Miary asymetrii – współczynniki asymetrii
4.
Miary koncentracji
•
współczynnik skupienia – kurtoza,
•
nierównomierny podział zjawiska w zbiorowości – miara Lorenza
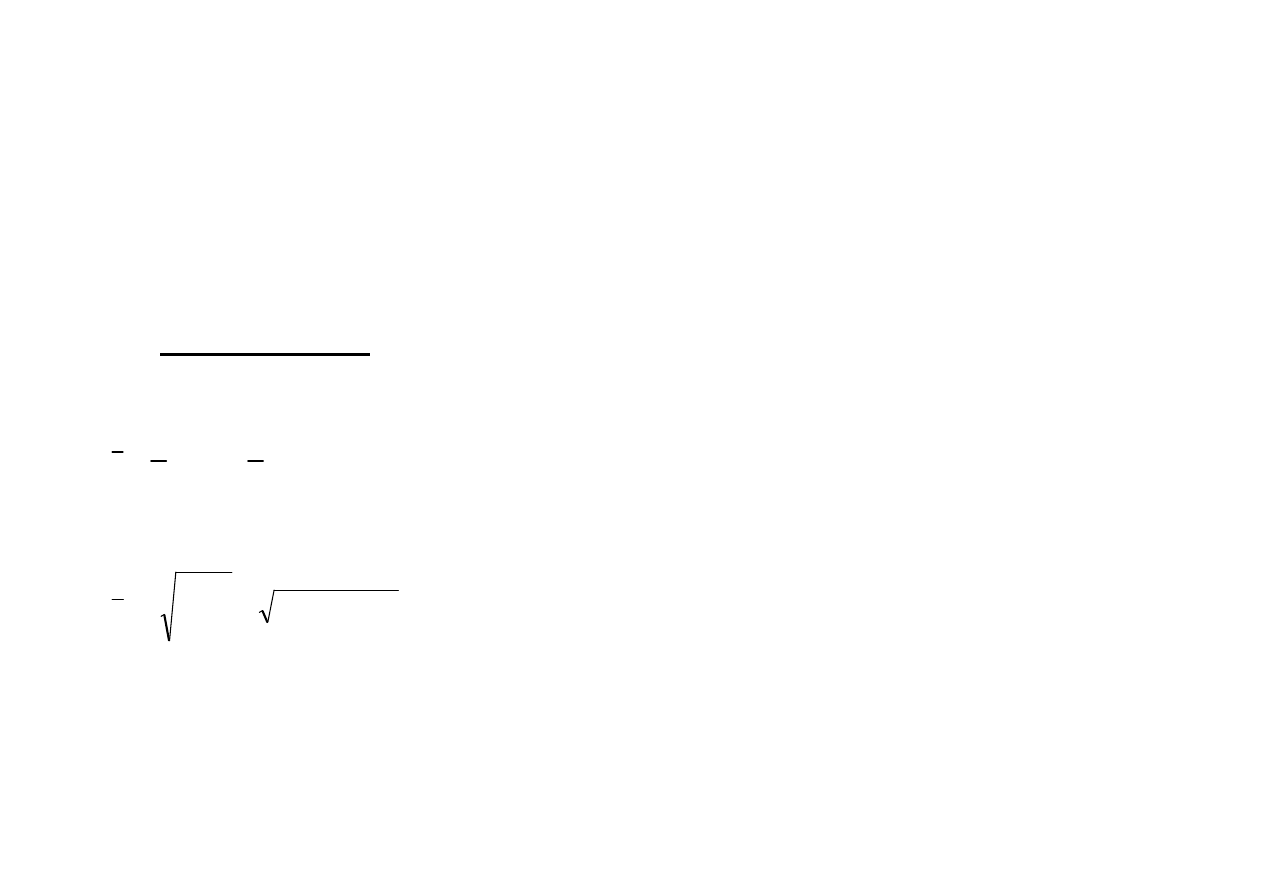
dr A. Czech
3
Zaprezentowane charakterystyki liczbowe znajdują zastosowanie do opisu
materiału statystycznego zgromadzonego w postaci szeregów: szczegółowy,
rozdzielczy (punktowy, przedziałowy)
I. SZEREG SZCZEGÓŁOWY – gdy dysponujemy n indywidualnymi obserwacjami
n
x
x
x
,...,
,
2
1
gdzie n – liczba obserwacji w próbie
1.
Miary położenia
a) średnia arytmetyczna (nieważona, prosta) –suma wartości cechy mierzalnej przez
liczbę skończonej zbiorowości statystycznej
)
...
(
1
1
2
1
1
n
n
i
i
x
x
x
n
x
n
x
+
+
+
=
=
∑
=
gdzie:
i
x - i-ty element próby (i = 1,2,...,n),
b) średnia geometryczna – znajduje zastosowanie w badaniach średniego tempa zmian
zjawiska (ujęcie dynamiczne dotyczy szeregów czasowych)
n
n
n
n
i
i
g
x
x
x
x
x
⋅
⋅
⋅
=
=
∏
=
...
2
1
1
c) średnia harmoniczna - stosuje się gdy cechy podawane są w przeliczeniu na
jednostkę innej cechy (wskaźniki natężenia), wagi zaś w jednostkach liczników tych
cech np.: prędkość pojazdu w km/h (waga –km), pracochłonność w min/sztukę (waga
– czas w min
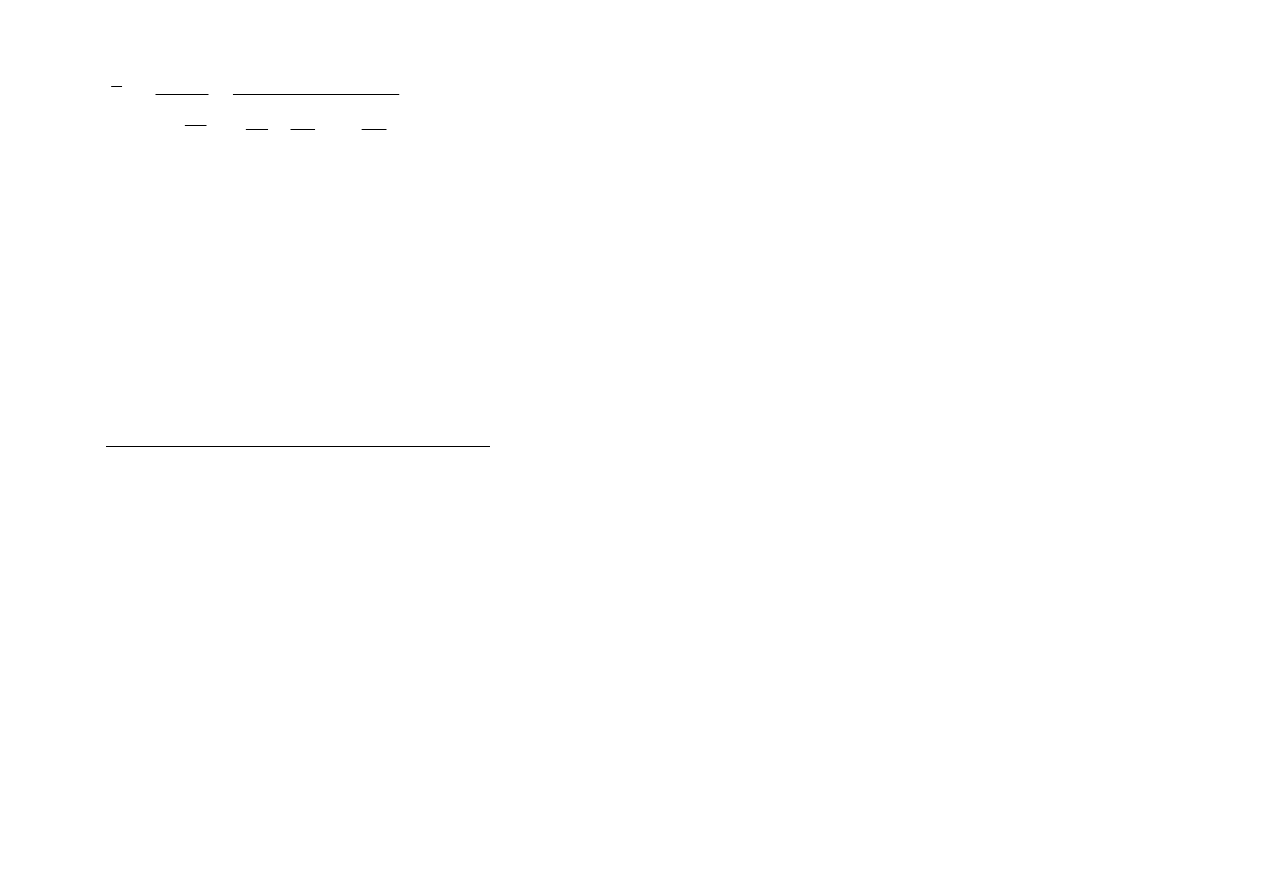
dr A. Czech
4
+
+
=
=
∑
=
n
n
i
i
h
x
x
x
n
x
n
x
1
...,
1
1
1
2
1
1
d) modalna (moda, dominanta, wartość najczęstsza)
D
M
o
,
– wartość cechy, która w
danym rozkładzie empirycznym występuje najczęściej
e) kwantyle – wartości cechy przedstawionej w postaci szeregu statystycznego, które
dzielą zbiorowość na określone części pod względem liczby obserwacji.
Najczęściej stosowane kwantyle:
•
kwartyl pierwszy
1
Q
- dzieli zbiór obserwacji na 2 części tak że: 25% wartości
cechy na wartości nie większe od
1
Q
a 75% nie mniejsze od
1
Q
•
kwartyl drugi (mediana
e
M
) – dzieli uporządkowaną monotonicznie (rosnąco)
zbiorowość na dwie równe części tak ze połowa wartości zmiennej jest mniejsza
lub równa medianie a druga połowa większa lub równa medianie
dr A. Czech
5
+
=
+
+
parzyste
jest
n
gdy
x
x
e
nieparzyst
jest
n
gdy
x
M
n
n
n
e
)
(
2
1
1
2
2
2
1
•
kwartyl trzeci
3
Q
-dzieli zbiorowość na 2 części tak że: 75% wartości cechy ma
wartości niewiększe od
3
Q
, a 25% obserwacji ma wartości niemniejsze od
3
Q
W szeregu szczegółowym
1
Q
oraz
3
Q
wyznacza się analogicznie jak medianę
dzieląc zbiorowość statystyczną na dwie równe części. Pierwsza – jednostki
przyjmują wartości cechy niewiększe od mediany. Druga – jednostki przyjmują
wartości niemniejsze od mediany.
Dla każdej ze zbiorowości należy ponownie wyznaczyć medianę:
Mediana dla pierwszej zbiorowości -
1
Q
Mediana dla drugiej zbiorowości -
3
Q
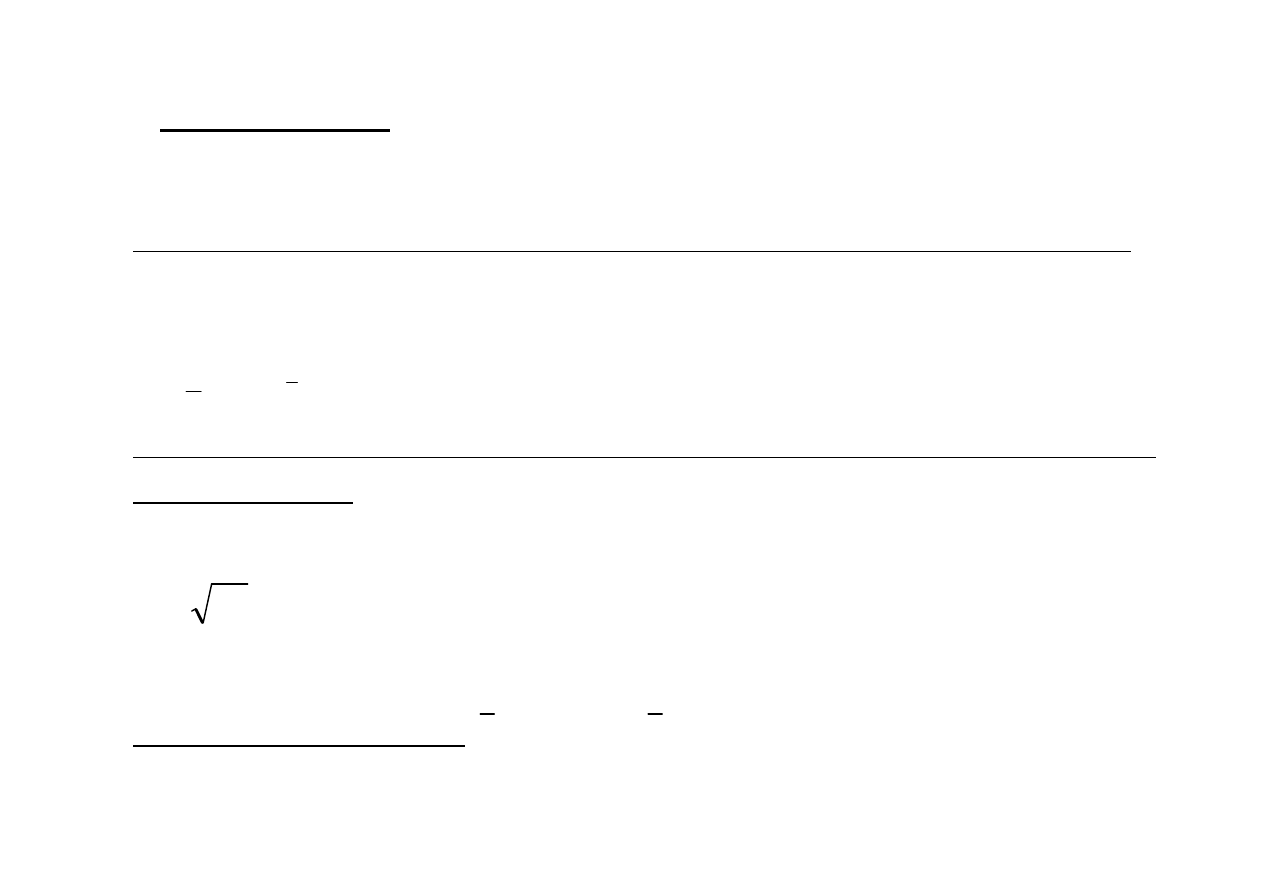
dr A. Czech
6
2.
Miary zmienności
a) rozstęp
min
max
x
x
R
−
=
max
x
-
maksymalna wartość cechy,
min
x
- minimalna wartość cechy,
Nie daje informacji o zróżnicowanie poszczególnych wartości cechy w zbiorowości.
b) warjancja – średnia arytmetyczna kwadratów odchyleń poszczególnych wartości
cechy od jej średniej arytmetycznej
(
)
∑
=
−
=
n
i
i
x
x
n
s
1
2
2
1
Uwaga: nie interpretujemy wyników bo miana podniesione do kwadratu – nie ma
czegoś takiego jak
2
kg
c) odchylenie standardowe – pierwiastek kwadratowy z wariancji
2
s
s
=
Określa przeciętne zróżnicowanie poszczególnych wartości cechy od średniej
arytmetycznej
Typowy obszar zmienności:
s
x
x
s
x
typ
+
<
<
−
dr A. Czech
7
d) odchylenie przeciętne – średnia arytmetyczna bezwzględnych odchyleń wartości
cechy od jej średniej arytmetycznej
∑
=
−
=
n
i
i
x
x
n
d
1
1
e) odchylenie ćwiartkowe – połowa różnicy między trzecim i pierwszym kwartylem
2
1
3
Q
Q
Q
−
=
Jest to parametr umożliwiający określenie odchylenia wartości cechy od jej mediany
Typowy obszar zmienności:
Q
M
x
Q
M
e
typ
e
+
<
<
−
Wszystkie przedstawiony miary zróżnicowania to miary bezwzględne – posiadają
miana
f) współczynnik zmienności – iloraz bezwzględnej miary zmienności i jej przeciętnej
•
klasyczny współczynnik zmienności
x
s
V
s
=
•
pozycyjny współczynnik zmienności
e
e
Q
M
Q
Q
M
Q
V
2
1
3
−
=
=
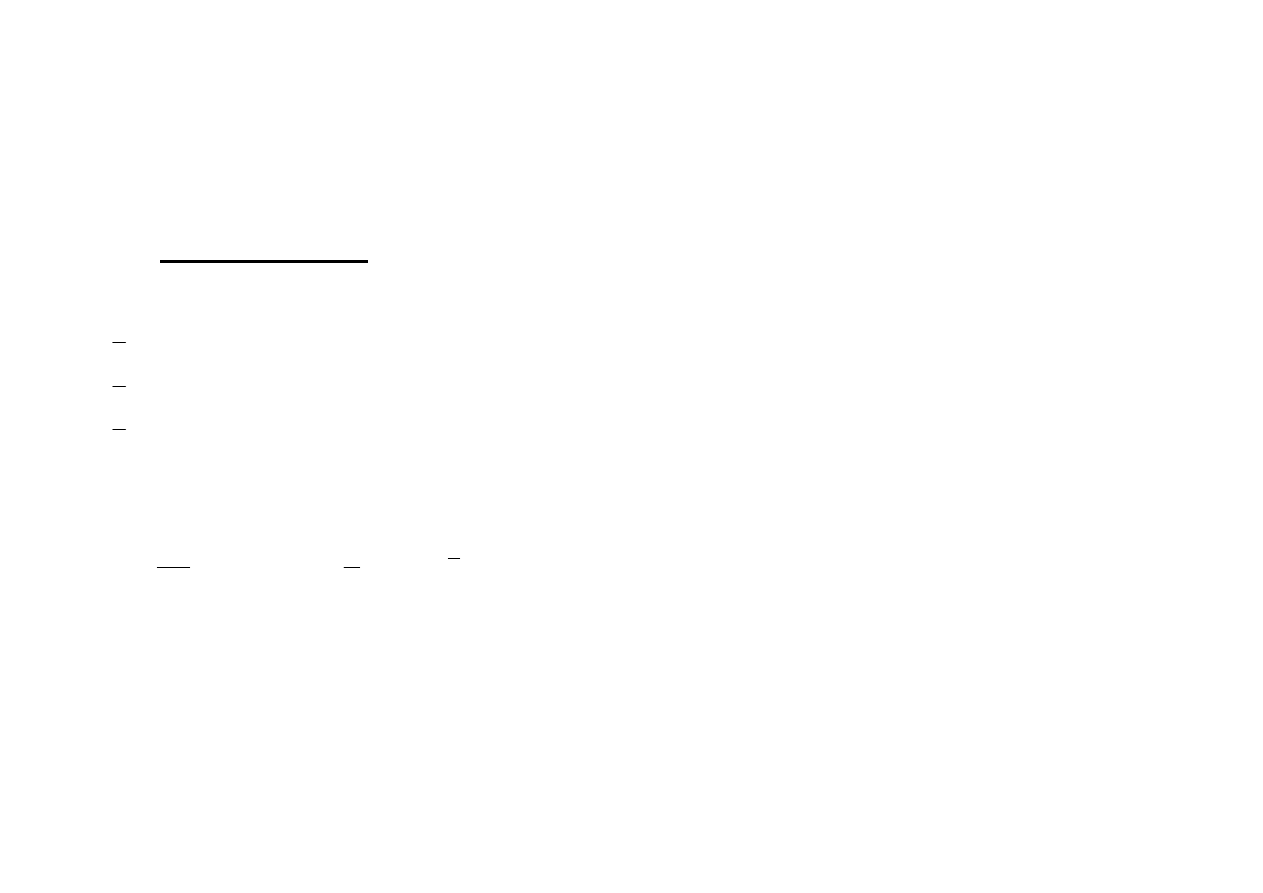
dr A. Czech
8
1
,
0
,
<
Q
s
V
V
- niskie zróżnicowanie zmiennej,
1
,
0
,
>
Q
s
V
V
- wysokie zróżnicowanie zmiennej (niejednorodność zbiorowości).
3.
Miary asymetrii
Porównujemy dominantę, medianę i średnią arytmetyczną – sposób najprostszy
D
M
x
e
=
=
- rozkład symetryczny
D
M
x
e
>
>
- asymetria prawostronna (przewaga niskich wartości cechy)
D
M
x
e
<
<
- asymetria lewostronna (przewaga wysokich wartości cechy)
Klasyczny współczynnik asymetrii (moment standaryzowany trzeciego rzędu)
3
3
s
m
A
=
gdzie:
(
)
∑
−
=
3
3
1
x
x
n
m
i
- moment trzeciego rzędu
0
=
A
- rozkład symetryczny,
Kierunek asymetrii
0
>
A
- asymetria prawostronna,
0
<
A
- asymetria lewostronna.
Siła asymetrii
1
<
A
lub
1
−
>
A
jeżeli blisko zera to asymetria łagodna,
1
>
A
lub
1
−
<
A
asymetria skrajna.
dr A. Czech
9
4.
Miary koncentracji
Współczynnik skupienia (Kurtoza) – miara skupienia poszczególnych obserwacji
wokół średniej
4
4
s
m
K
=
gdzie:
(
)
∑
=
−
=
n
i
i
x
x
n
m
1
4
4
1
- moment czwartego rzędu
Wysoka wartość współczynnika K - wysmukła krzywa liczebności – większa
koncentracja wartości cechy wokół średniej
Mała wartość współczynnika K - spłaszczona krzywa liczebności – mała koncentracja
wartości cechy wokół średniej
K=3 – rozkład normalny,
K<3 – rozkład bardziej spłaszczony od normalnego,
K>3 – rozkład bardziej wysmukły od normalnego,
3
4
4
−
=
′
s
m
K
- eksces
0
=
′
K
– rozkład normalny,
0
<
′
K
– rozkład bardziej spłaszczony od normalnego,
0
>
′
K
– rozkład bardziej wysmukły od normalnego,
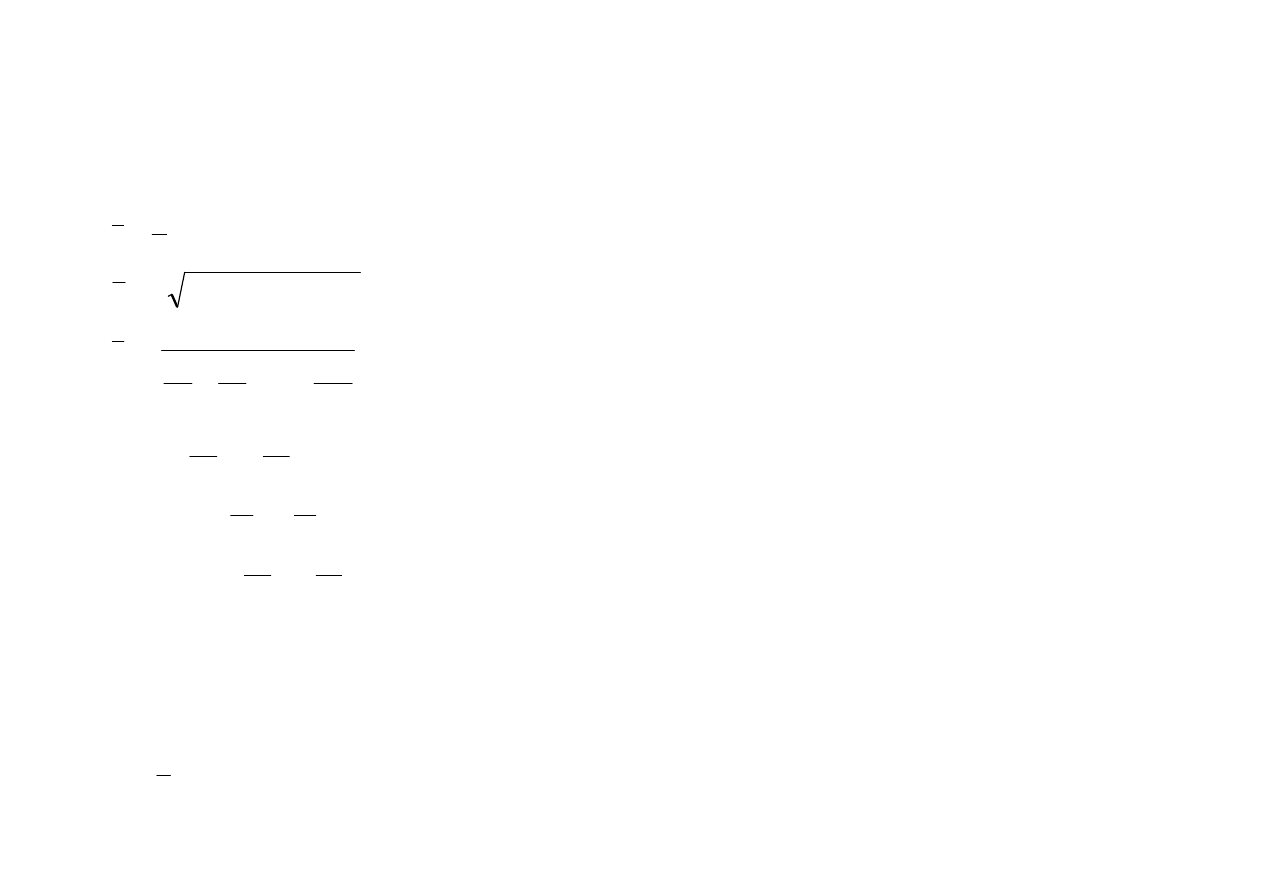
dr A. Czech
10
PRZYKŁAD ZASTOSOWANIA MIAR OPISOWYCH (SZEREG SZCZEGÓŁOWY)
Ad 1. Miary położenia
{
}
103
,
102
,
100
,
98
,
97
=
i
x
- ceny towaru w 5 sklepach; n=5
(
)
100
103
...
98
97
5
1
=
+
+
+
=
x
- średnia arytmetyczna
(stosujemy)
(
)
974
,
99
103
...
98
97
5
=
⋅
⋅
⋅
=
g
x
- średnia geometryczna
(przykład kalkulacji)
948
,
99
103
1
...
98
1
97
1
5
=
+
+
+
=
h
x
- średnia harmoniczna
(przykład kalkulacji)
100
3
2
1
5
2
1
=
=
=
=
+
+
x
x
x
M
n
e
- mediana
98
2
2
1
3
2
1
1
=
=
=
=
=
+
+
x
x
x
M
Q
n
e
- kwartyl pierwszy, gdzie:
{
}
100
,
98
,
97
102
2
2
1
3
2
1
3
=
=
=
=
=
+
+
x
x
x
M
Q
n
e
- kwartyl trzeci gdzie:
{
}
103
,
102
,
100
)
(D
M
o
- brak dominanty (wariany cechy występują z jednakową częstością)
Ad 2. Miary zróżnicowania
6
97
103
=
−
=
R
- rozstęp
[
]
2
,
5
)
100
103
(
...
)
100
98
(
)
100
97
(
5
1
2
2
2
2
=
−
+
+
−
+
−
=
s
- wariancja
(nie interpretujemy !!!!)
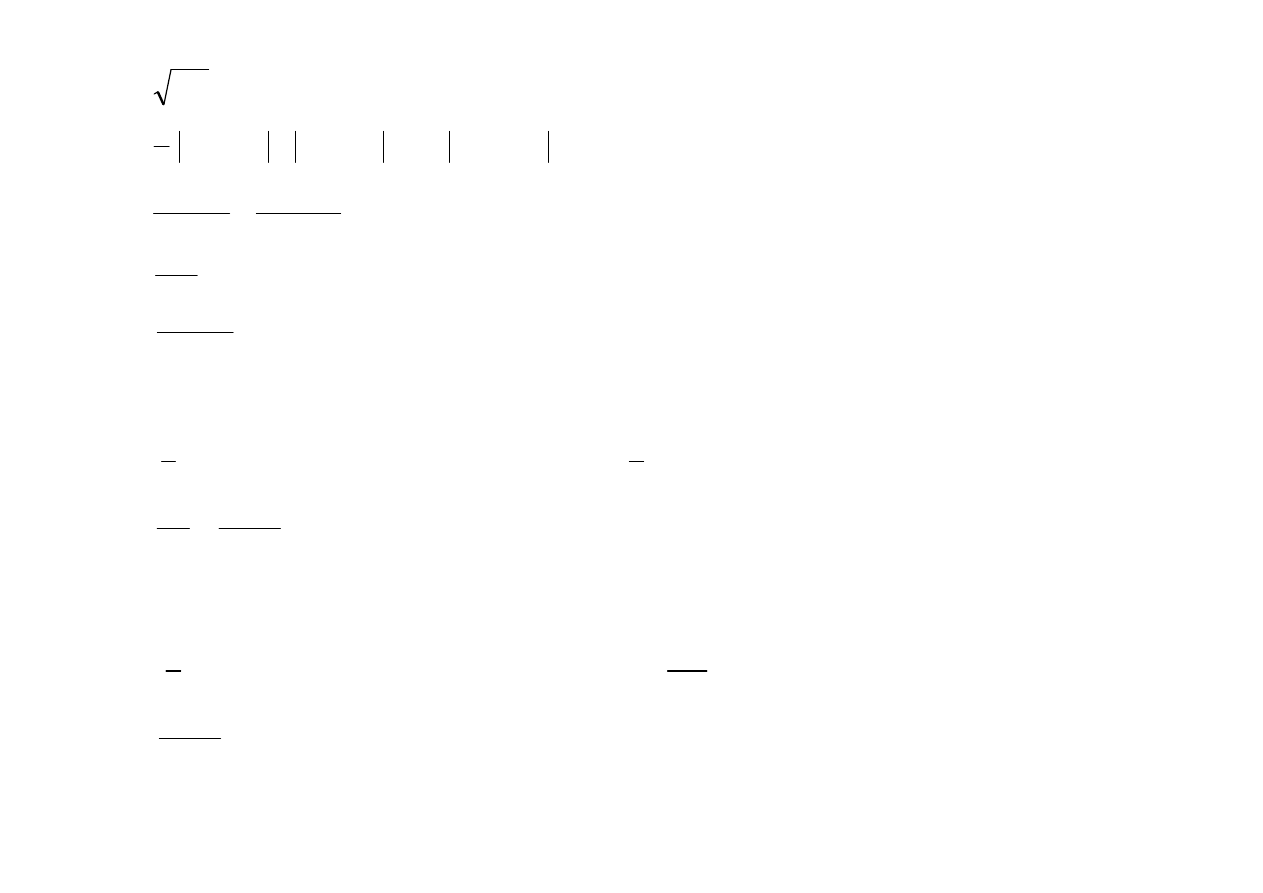
dr A. Czech
11
28
,
2
2
,
5
=
=
s
- odchylenie standardowe
[
]
2
100
103
...
100
98
100
97
5
1
=
−
+
+
−
+
−
=
d
- odchylenie przeciętne
2
2
98
102
2
1
3
=
−
=
−
=
Q
Q
Q
- odchylenie ćwiartkowe
%
28
,
2
100
100
28
,
2
=
=
S
V
- klasyczny współczynnik zmienności
%
2
100
100
2
98
102
=
⋅
−
=
Q
V
- pozycyjny współczynnik zmienności
Ad 3.Miary asymetrii
[
]
0
5
0
)
100
103
(
...
)
100
98
(
)
100
97
(
5
1
3
3
3
3
=
=
−
+
+
−
+
−
=
m
- moment trzeciego rzędu
0
28
,
2
0
3
3
3
=
=
=
s
m
A
- rozkład zgodny z rozkładem normalnym (idealnie symteryczny)
Ad 4.Miary koncentracji
[
]
8
,
38
5
194
)
100
103
(
...
)
100
98
(
)
100
97
(
5
1
4
4
4
4
=
=
−
+
+
−
+
−
=
m
- moment czwartego rzędu
436
,
1
28
,
2
8
,
38
4
=
=
K
- kurtoza
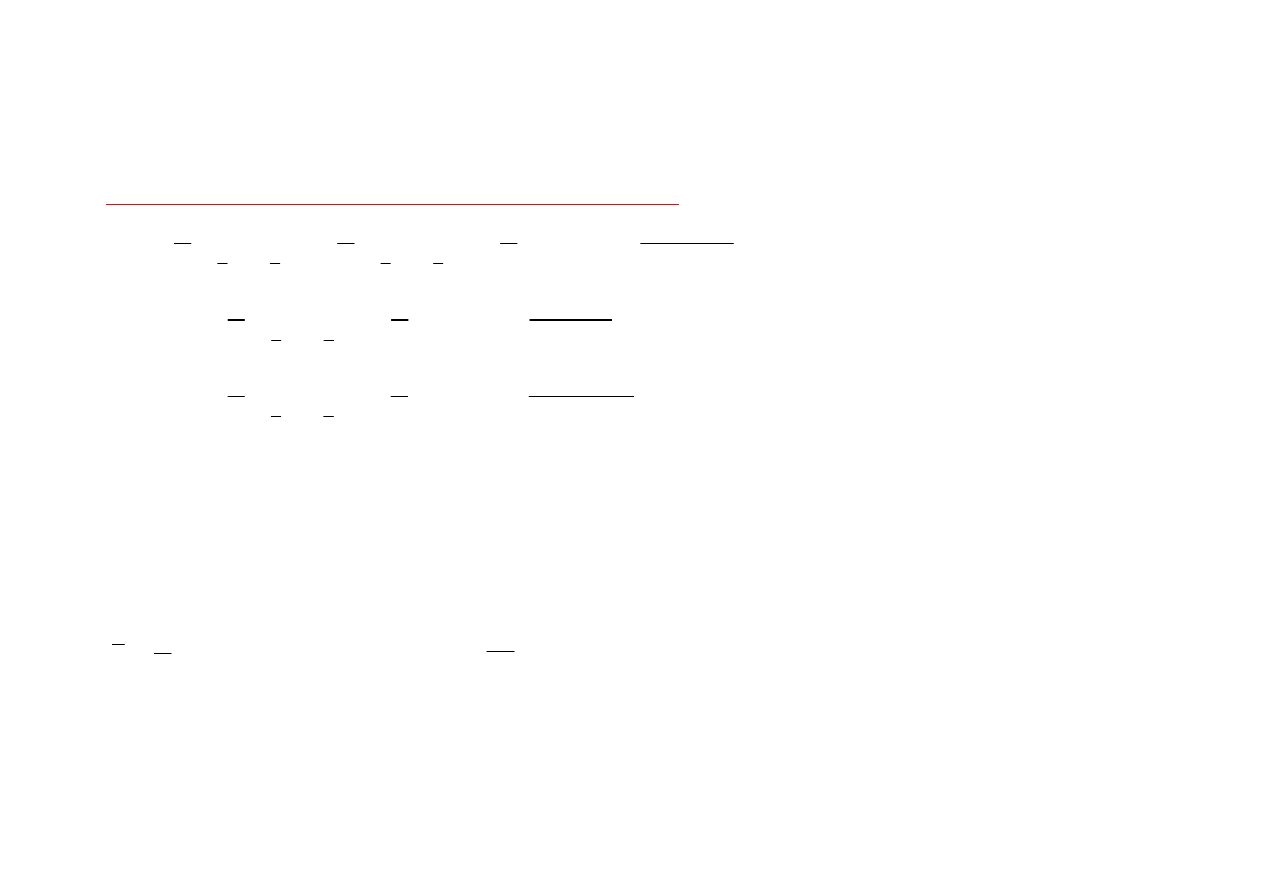
dr A. Czech
12
564
,
1
3
436
,
1
−
=
−
=
′
K
- eksces (wykres spłaszczony w porównaniu do wykresu
normalnego)
Przypadek parzystej liczby obserwacji w próbie
{
}
,
102
,
100
,
98
,
97
=
X
, n=4
99
2
100
98
)
(
2
1
)
(
2
1
)
(
2
1
3
2
1
2
4
2
4
1
2
2
=
+
=
+
=
+
=
+
=
+
+
x
x
x
x
x
x
M
n
n
e
- mediana
5
,
97
2
98
97
)
(
2
1
)
(
2
1
2
1
1
2
2
2
1
=
+
=
+
=
+
=
=
+
x
x
x
x
M
Q
n
e
- kwartyl pierwszy, gdzie: {97,98}
101
2
102
100
)
(
2
1
)
(
2
1
2
1
1
2
2
2
1
=
+
=
+
=
+
=
=
+
x
x
x
x
M
Q
n
e
- kwartyl trzeci. gdzie: {100, 102}
Pozostałe charakterystyki liczymy analogicznie do zaprezentowanych
II. SZEREG ROZDZIELCZY PUNKTOWY
a) średnia arytmetyczna ważona
∑
∑
=
=
=
=
k
i
i
i
k
i
i
i
x
w
x
n
n
x
1
1
1
bo
n
n
w
i
i
=
- średnia arytmetyczna ważona
b) modalna (moda, dominanta, wartość najczęstsza)
D
M
o
,
– wartość cechy, której
odpowiada największa liczebność bądź częstość
dr A. Czech
13
c) kwantyle
e
isk
m
w
⇒
≥
∑
5
,
0
- mediana (kwartyl drugi),
1
25
,
0
Q
w
isk
⇒
≥
∑
- kwartyl pierwszy,
3
75
,
0
Q
w
isk
⇒
≥
∑
- kwartyl trzeci.
d) odchylenie standardowe – pierwiastek kwadratowy z wariancji
2
s
s
=
gdzie:
∑
=
−
=
k
i
i
i
n
x
x
n
s
1
2
2
)
(
1
- warjancja
e) współczynnik asymetrii
3
3
s
m
A
=
gdzie:
∑
=
−
=
k
i
i
i
n
x
x
n
m
1
3
3
)
(
1
- moment trzeciego rzędu
f) kurtoza
4
4
s
m
K
=
gdzie:
∑
=
−
=
k
i
i
i
n
x
x
n
m
1
4
4
)
(
1
- moment czwartego rzedu
dr A. Czech
14
PRZYKŁAD ZASTOSOWANIA MIAR OPISOWYCH (SZEREG ROZDZIELCZY
PUNKTOWY)
Przykład: Oceny z matematyki (100 studentów)
675
,
3
5
,
367
100
1
1
6
1
=
=
=
∑
=
i
i
i
x
n
n
x
lub
675
,
3
6
1
=
=
∑
=
i
i
i
x
w
x
- średnia arytmetyczna
5
,
3
=
o
M
- dominanta (liczębność bądz częstość największa)
5
,
3
5
,
0
=
⇒
≥
∑
e
isk
M
w
- mediana (kwartyl drugi),
3
25
,
0
1
=
⇒
≥
∑
Q
w
isk
- kwartyl pierwszy
4
75
,
0
3
=
⇒
≥
∑
Q
w
isk
- kwartyl trzeci
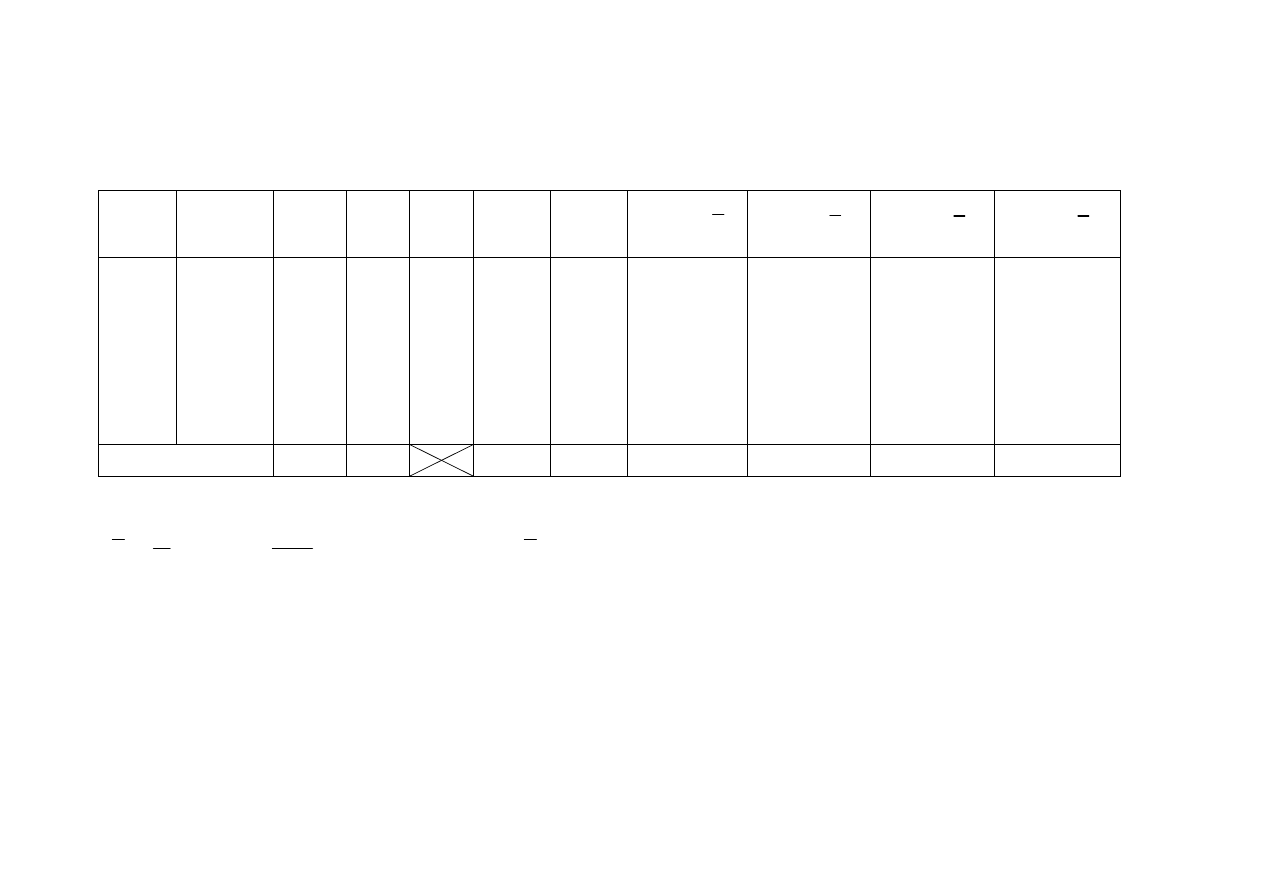
Klasy
i
Ocena
stud.
i
x
Stud.
i
n
i
w
isk
w
i
i
x
n
i
i
x
w
)
(
x
x
n
i
i
−
2
)
(
x
x
n
i
i
−
3
)
(
x
x
n
i
i
−
4
)
(
x
x
n
i
i
−
1
2
3
4
5
6
2
3
3,5
4
4,5
5
5
20
35
20
10
10
0,05
0,20
0,35
0,20
0,10
0,10
0,05
0,25
0,60
0,80
0,90
1
10
60
122,5
80
45
50
0,10
0,60
1,225
0,80
0,45
0,50
-8,375
-13,5
-6,125
6,5
8,25
13,25
14.028
9,113
1,072
2,113
6,806
17,556
-23,497
-6,151
-0,188
0,678
5,615
23,262
39,358
4,152
0,033
0,223
4,633
30,822
Suma
100
1
367,5 3,675
0
50,688
-0,272
79,220
dr A. Czech
15
507
,
0
688
,
50
100
1
)
(
1
1
2
2
=
=
−
=
∑
=
k
i
i
i
x
x
n
n
s
- warjancja
712
,
0
507
,
0
2
=
=
=
s
s
- odchylenie standardowe
00272
,
0
)
272
,
0
(
100
1
)
(
1
1
3
3
−
=
−
=
−
=
∑
=
k
i
i
i
x
x
n
n
m
- moment trzeciego rzędu
0075
.
0
712
,
0
00272
,
0
3
3
3
−
=
−
=
=
s
m
A
- współczynnik asymetrii
0,7922
79,220
100
1
)
(
1
1
4
4
=
=
−
=
∑
=
k
i
i
i
x
x
n
n
m
- moment czwartego rzedu
082
,
3
257
,
0
7922
,
0
4
4
=
=
=
s
m
K
- kurtoza
082
,
0
3
082
,
3
3
=
−
=
−
=
′
K
K
- eksces
II. SZEREG ROZDZIELCZY PRZEDZIAŁOWY
a) średnia arytmetyczna ważona
∑
∑
=
=
=
=
k
i
i
i
k
i
i
i
x
w
x
n
n
x
1
1
1
&
&
gdzie:
n
n
w
i
i
=
- wskaźnik struktury (częstość)
2
1
0
i
i
i
x
x
x
+
=
•
-środek i-tego przedziału klasowego i=1,2,...,k
dr A. Czech
16
i
x
1
- górna granica i-tego przedziału klasowego,
i
x
0
- dolana granica i-tego przedziału klasowego
b) modalna (moda, dominanta, wartość najczęstsza)
D
M
o
,
– w szeregach
rozdzielczych przedziałowych można określić tylko przedział zawierający dominantę
Przybliżoną wartość dominanty otrzymuje się na dwa sposoby:
•
wzór interpolacyjny
m
m
m
m
m
m
m
m
o
h
n
n
n
n
n
n
x
M
)
(
)
(
1
1
1
0
+
−
−
−
+
−
−
+
=
gdzie:
m
- numer przedziału (klasy), w którym występuje modalna,
m
x
0
- dolna granica przedziału, w którym występuje modalna,
m
n
- liczebność przedziału modalnej, tzn, klasy o numerze m,
1
1
;
+
−
m
m
n
n
- liczebność klas: poprzedzającej przedział modalnej i następującej
po tym przedziale, tzn. o numerach m-1 i m+1,
m
h
- rozpiętość przedziału klasowego, w którym znajduje się modalna.
•
graficznie z histogramu liczebności (częstości)
dr A. Czech
17
c) kwantyle
kwartyl drugi (mediana
e
M
)
m
m
m
i
i
Me
m
e
h
n
n
N
x
M
∑
−
=
−
+
=
1
1
0
kwartyl pierwszy
1
Q
m
m
m
i
i
Q
m
h
n
n
N
x
Q
∑
−
=
−
+
=
1
1
0
1
1
kwartyl trzeci
3
Q
m
m
m
i
i
Q
m
h
n
n
N
x
Q
∑
−
=
−
+
=
1
1
0
3
3
gdzie:
m
- numer przedziału (klasy), w którym występuje odpowiadający mu kwartyl
m
x
0
- dolna granica przedziału, w którym występuje odpowiadający mu kwartyl
m
n
- liczebność przedziału, w którym występuje odpowiadający mu kwartyl
∑
−
=
1
1
m
i
i
n
- suma liczebności przedziałów poprzedzających odpowiedni kwartyl
(liczebność skumulowana)
m
h
- rozpiętość przedziału klasowego, w którym znajduje się odpowiedni
kwartyl
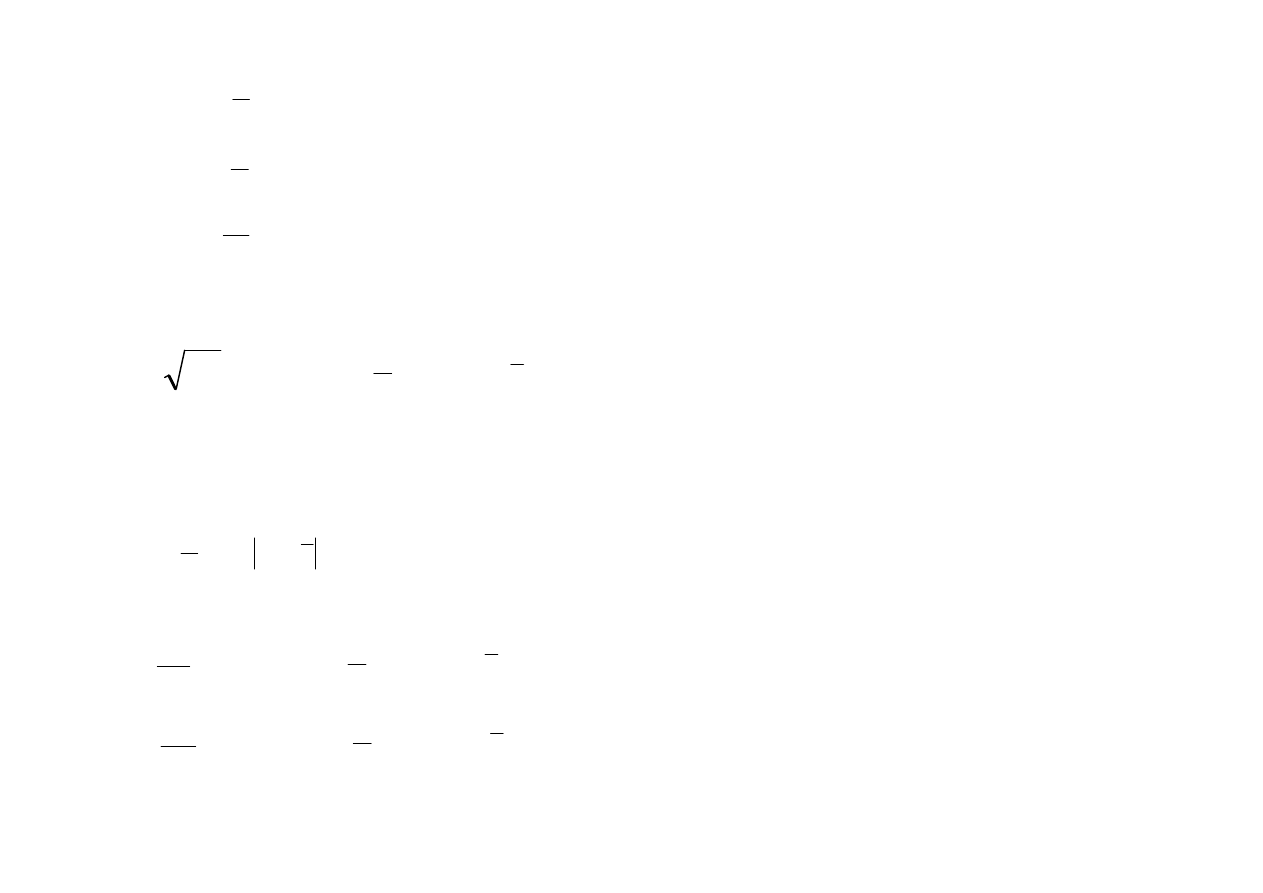
dr A. Czech
18
2
n
N
Me
=
- pozycja mediany (kwartyla drugiego),
4
1
n
N
Q
=
- pozycja kwartyla pierwszego,
4
3
3
n
N
Q
=
- pozycja kwartyla trzeciego.
d) odchylenie standardowe – pierwiastek kwadratowy z wariancji
2
s
s
=
gdzie:
∑
=
−
=
k
i
i
i
x
x
n
n
s
1
2
2
)
(
1
&
d) odchylenie przeciętne – średnia arytmetyczna bezwzględnych odchyleń wartości
cechy od jej średniej arytmetycznej
∑
=
−
=
n
i
i
i
x
x
n
n
d
1
1
&
e) współczynnik asymetrii
3
3
s
m
A
=
gdzie:
∑
=
−
=
k
i
i
i
x
x
n
n
m
1
3
3
)
(
1
&
- moment trzeciego rzędu
4
4
s
m
K
=
gdzie:
∑
=
−
=
k
i
i
i
x
x
n
n
m
1
4
4
)
(
1
&
- moment czwartego rzędu
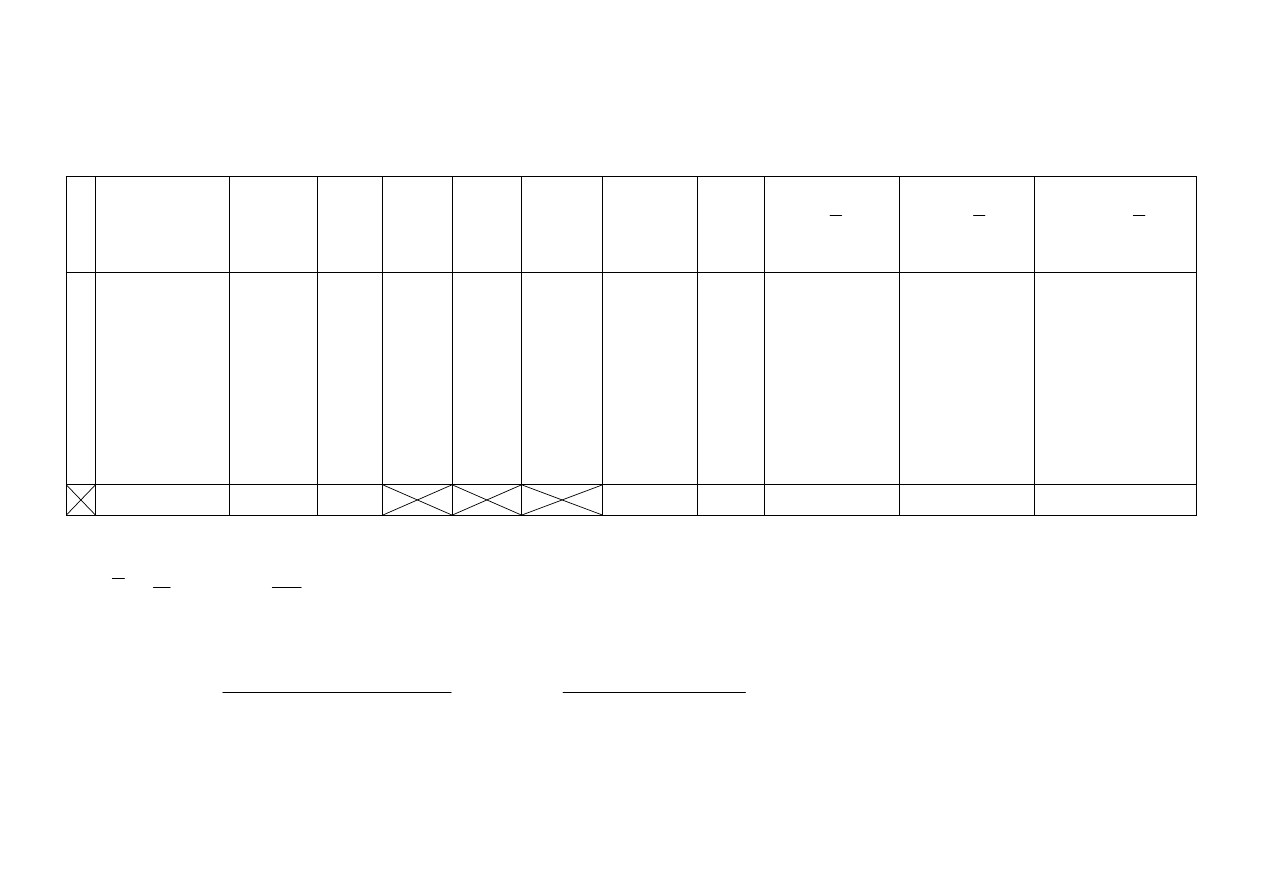
dr A. Czech
19
PRZYKŁAD ZASTOSOWANIA MIAR OPISOWYCH (SZEREG PRZEDZIAŁOWY)
Przykład wydatki 50-ciu gospodarstw domowych na paliwo
454
22700
50
1
1
1
=
=
=
∑
=
k
i
i
i
x
n
n
x
&
- średnia arytmetyczna,
55
,
454
100
)
10
20
(
)
8
20
(
8
20
400
)
(
)
(
1
1
1
0
=
−
+
−
−
+
=
−
+
−
−
+
=
+
−
−
m
m
m
m
m
m
m
m
o
h
n
n
n
n
n
n
x
M
- modalna
i
Przedziały
i
x
Gosp.
dom.
i
n
i
w
isk
n
isk
w
i
x
&
i
i
n
x
&
i
i
w
x
&
i
i
n
x
x
2
)
(
−
&
i
i
n
x
x
3
)
(
−
&
i
i
n
x
x
4
)
(
−
&
1
2
3
4
5
6
7
100-200
200-300
300-400
400-500
500-600
600-700
700-800
2
4
8
20
10
4
2
0,04
0,08
0,16
0,40
0,20
0,08
0,04
2
6
14
34
44
48
50
0,04
0,12
0,28
0,68
0,88
0,96
1
150
250
350
450
550
650
750
300
1000
2800
9000
5500
2600
1500
6
20
56
180
110
52
30
184832
166464
86528
320
92160
153664
175232
-56188928
-33958656
-8998912
-1280
8847360
30118144
51868672
17081434112
6927565824
935886848
5120
849346560
5903156224
15353126912
Suma
50
1
22700 454
859200
-8313600 47050521600
dr A. Czech
20
Graficzny sposób wyznaczania dominanty
i
w
i
x
o
M
455
100
20
14
2
50
400
1
1
0
=
−
+
=
−
+
=
∑
−
=
m
m
m
i
i
Me
m
e
h
n
n
N
x
M
- mediana
25
,
381
100
8
6
4
50
300
1
1
0
1
1
=
−
+
=
−
+
=
∑
−
=
m
m
m
i
i
Q
m
h
n
n
N
x
Q
- kwartyl pierwszy
dr A. Czech
21
535
100
10
34
4
50
3
500
1
1
0
3
3
=
−
⋅
+
=
−
+
=
∑
−
=
m
m
m
i
i
Q
m
h
n
n
N
x
Q
- kwartyl trzeci
Graficzny sposób wyznaczania kwantyli
isk
w
i
x
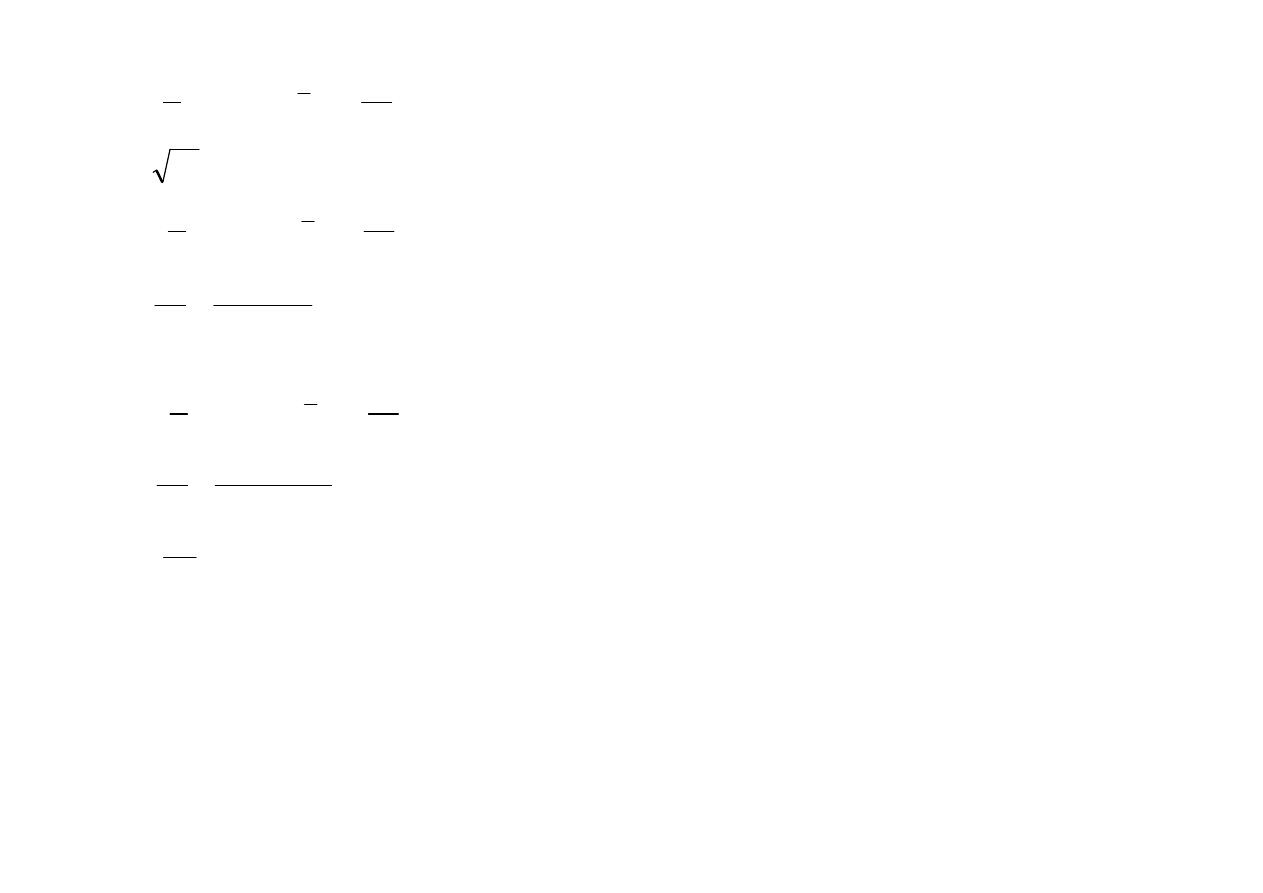
dr A. Czech
22
17184
859200
50
1
)
(
1
1
2
2
=
=
−
=
∑
=
k
i
i
i
x
x
n
n
s
&
- warjancja
09
,
131
2
=
=
s
s
- odchylenie standardowe
-166272
-8313600)
(
50
1
)
(
1
1
3
3
=
=
−
=
∑
=
k
i
i
i
x
x
n
n
m
&
moment trzeciego rzędu
074
,
0
09
,
131
166272
3
3
3
−
=
−
=
=
s
m
A
-
współczynnik
asymatrii
(rozkład
zbliżony
do
symetrycznego, bardzo lekka asymetria prawostronna)
941010432
0
4705052160
50
1
)
(
1
1
4
4
=
=
−
=
∑
=
k
i
i
i
x
x
n
n
m
&
- moment czwartego rzędu
19
,
3
131,09
941010432
4
4
4
=
=
=
s
m
K
- kurtoza
19
,
0
3
19
,
3
3
4
4
=
−
=
−
=
′
s
m
K
- eksces (wykres lekko wysmukły w porównaniu do wykresu
normalnego
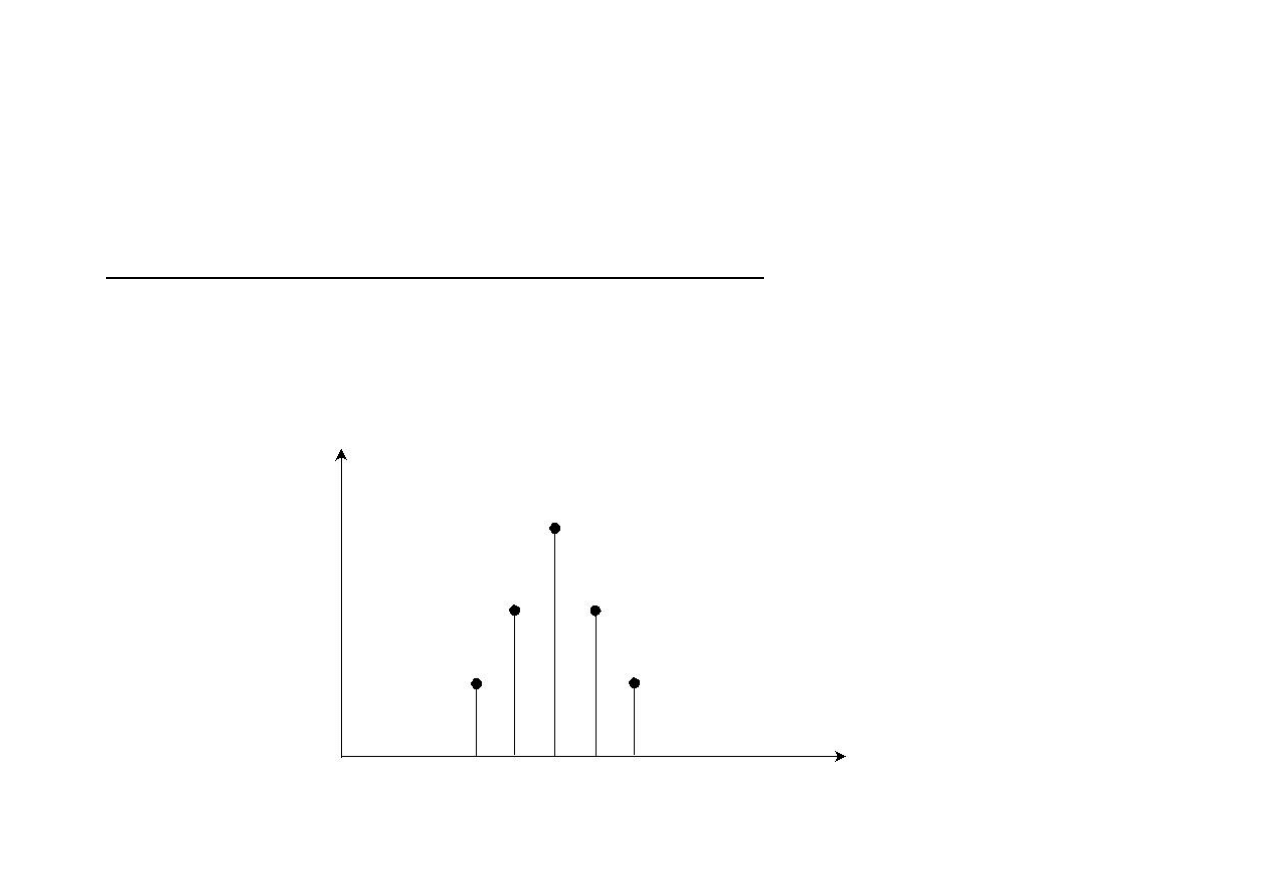
dr A. Czech
23
ROZKŁADY EMPIRYCZNE CECHY STASTYSTYCZNEJ
Rozkład empiryczny – przyporządkowane kolejnym wartościom cechy statystycznej
i
x
odpowiadające im liczebności
i
n
lub częstości
i
w
.
Rodzaje rozkładów empirycznych cechy statystycznej:
I. Cecha skokowa
A.
Jednomodalne – rozkład, którego diagram liczebności ma jedno maksimum
a)
symetryczne – liczebności odpowiadające wartościom cechy rozkładając się
symetrycznie wokół liczebności największej
i
n
i
x
D
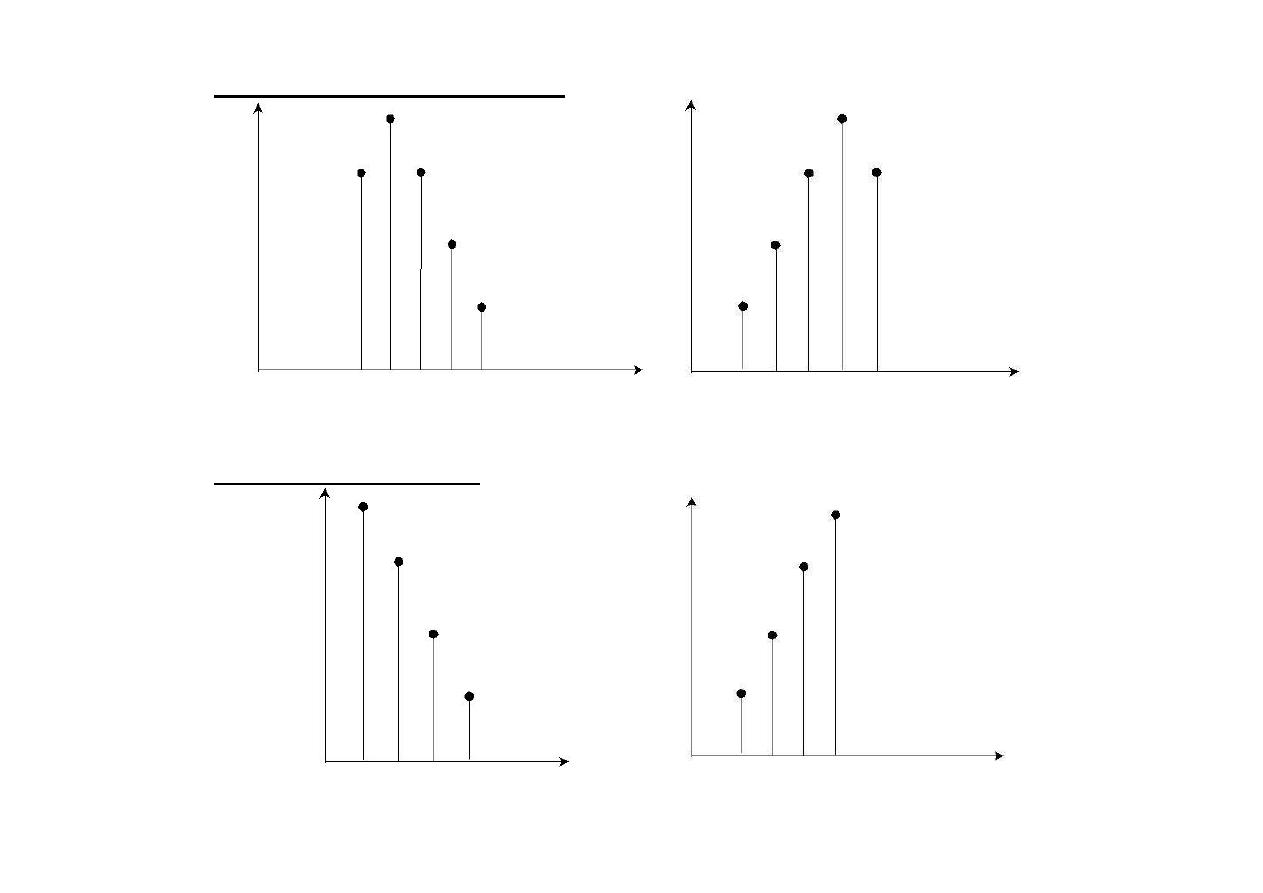
dr A. Czech
24
b)
umiarkowanie symetryczne,
i
n
i
n
i
x
i
x
asymetria prawostronna
asymetria lewostronna
c)
skrajnie symetryczne
asymetria prawostronna
asymetria lewostronna
dr A. Czech
25
B.
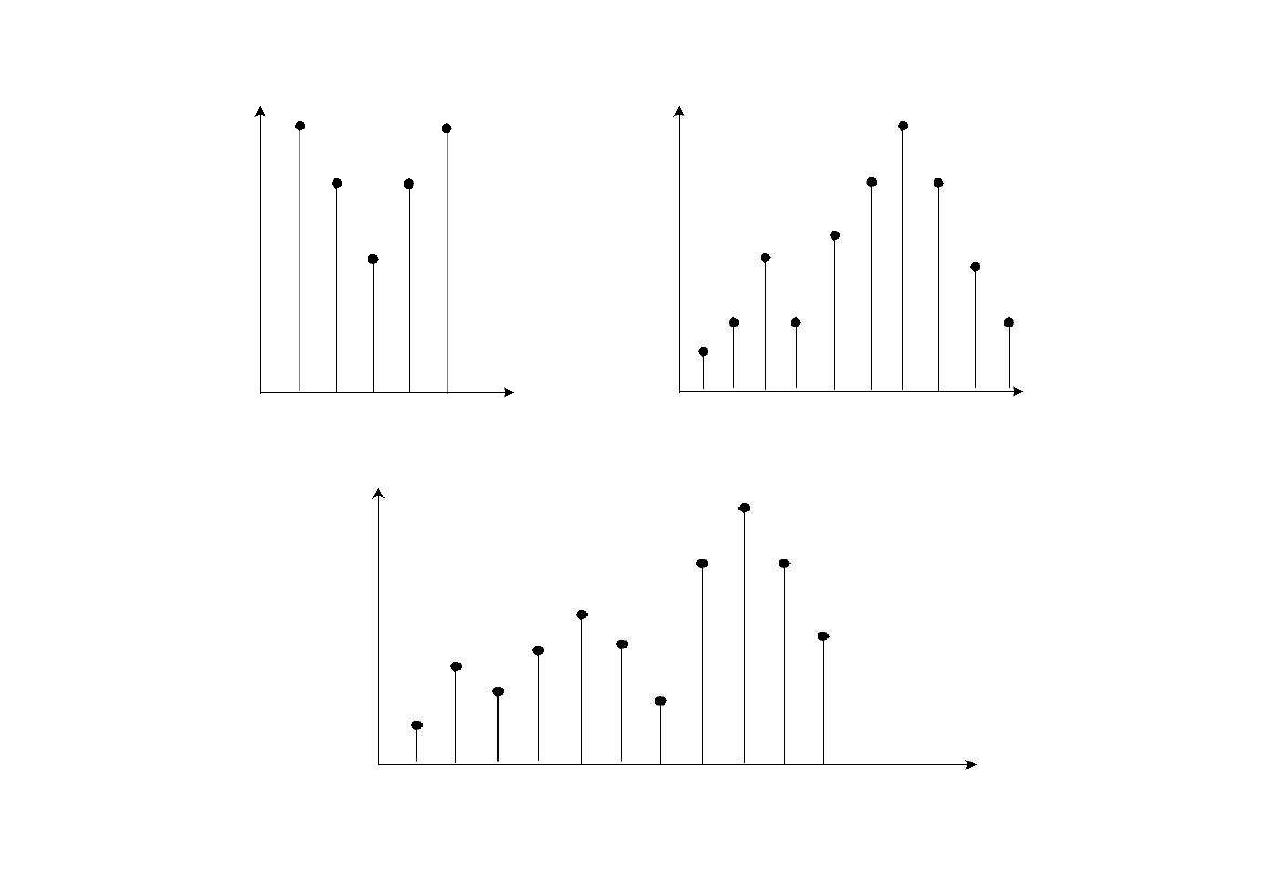
wielomodalne – posiadając co najmniej dwa ekstrema
i
n
i
n
i
x
i
x
Rozkład U (siodłowy)
Rozkład bimodalny
i
n
i
x
dr A. Czech
26
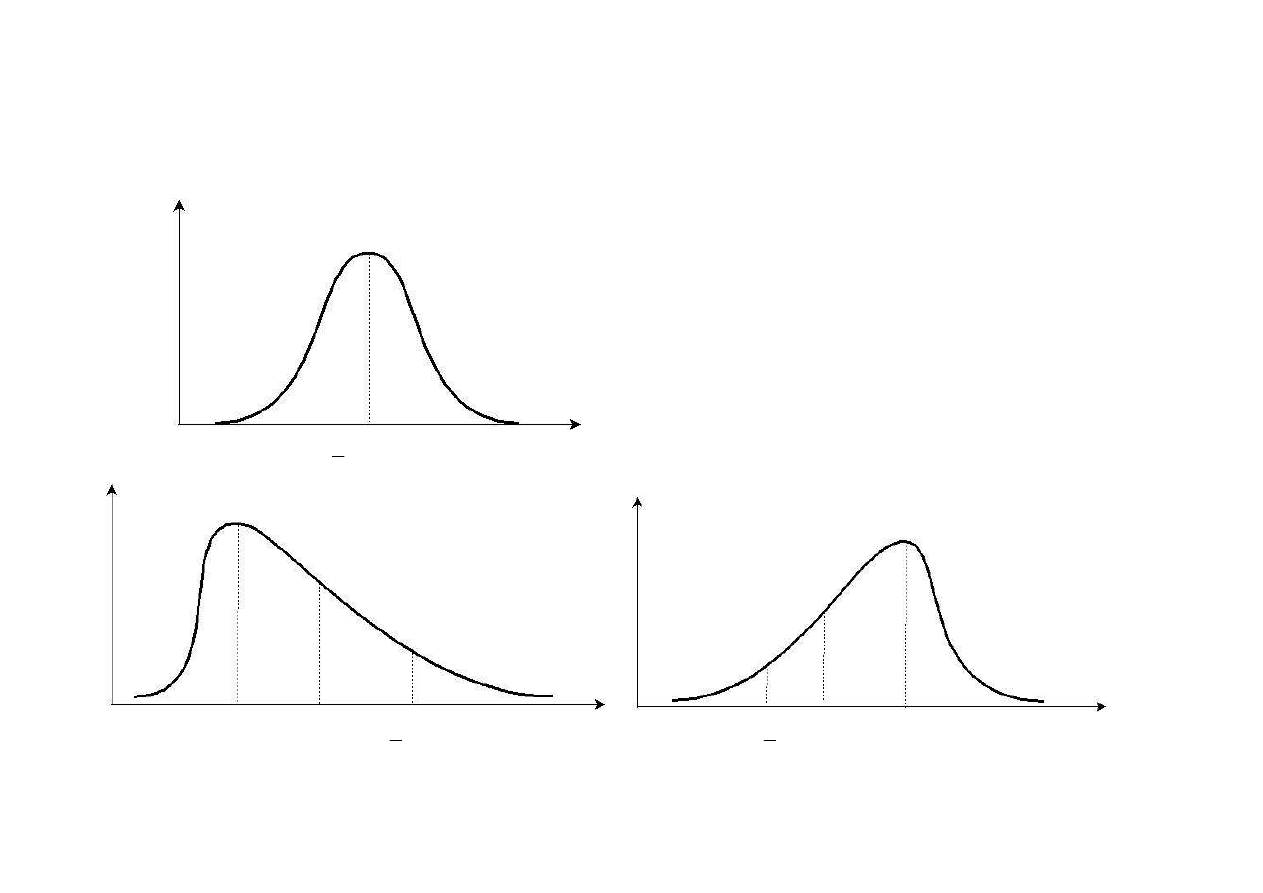
II. Cecha ciągła
A.
Jednomodalne - rozkład, którego krzywa liczebności ma jedno maksimum
a)
symetryczne – liczebności odpowiadające wartościom cechy rozkładając się
symetrycznie wokół liczebności największej
i
n
i
x
D
M
x
e
=
=
b) umiarkowanie symetryczne
i
n
i
n
i
x
i
x
x
M
D
e
<
<
D
M
x
e
<
<
asymetria prawostronna
asymetria lewostronna
dr A. Czech
27
b)
skrajnie symetryczne
i
n
i
n
i
x
i
x
asymetria prawostronna
asymetria lewostronna
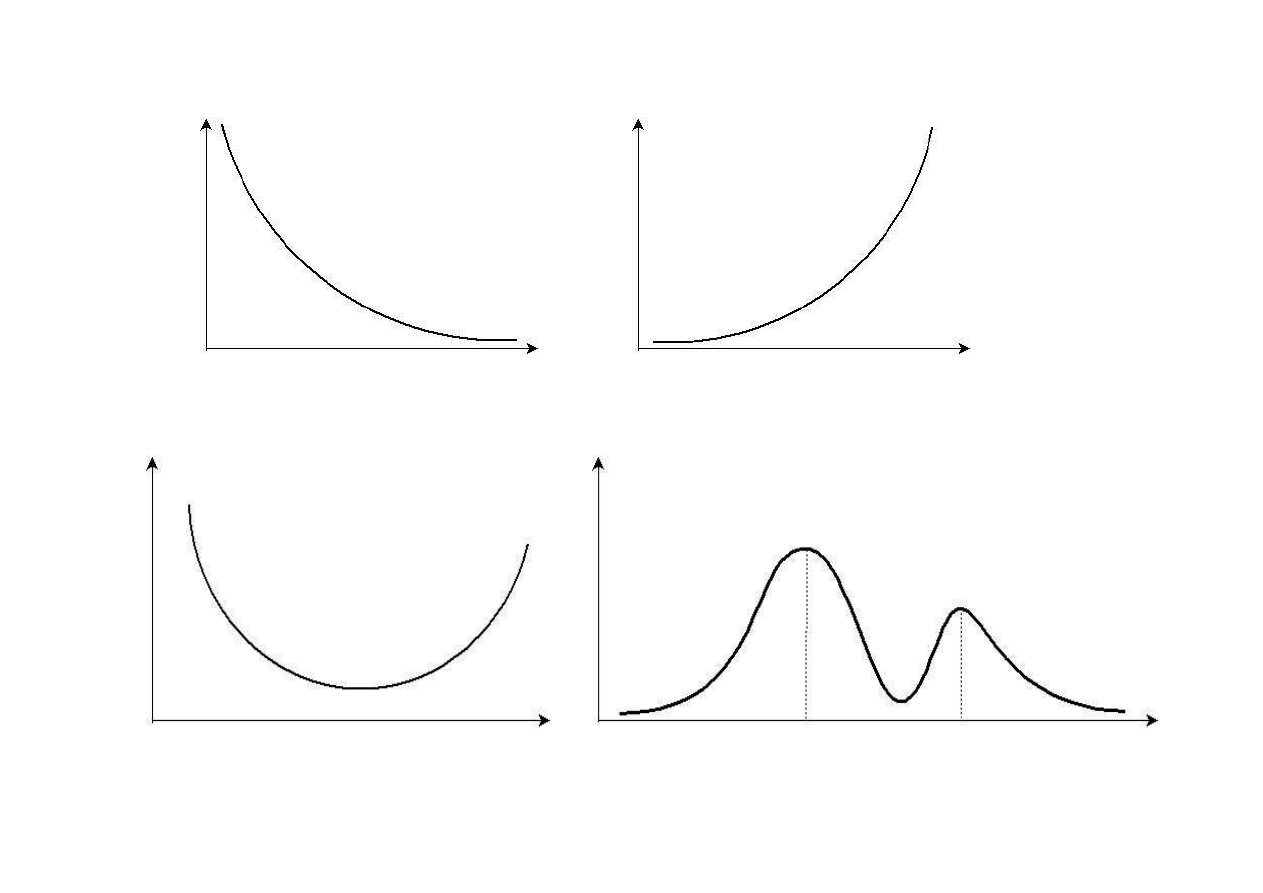
B.
Wielomodalne
i
n
i
n
i
x
i
x
Rozkład U (siodłowy)
Rozkład bimodalny