K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

1

MPiS30 W04: ZMIENNE LOSOWE I

1.

Zmienna losowa i jej rozkład

Przykład 1

2.

Niezależność zmiennych losowych

Przykład 2

3.

Dystrybuanty, ich własności i zastosowanie

Przykład 3

Przykład 4

Przykład 5

Przykład 6

4.

Zmienna losowa typu dyskretnego

Przykład 7

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

2

5.

Związek pomiędzy dystrybuantą a funkcją praw-

dop.

6.

Warunkowe zmienne losowe i ciągi niezależnych

prób

Przykład 8
Przykład 9

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

3

1. Zmienna losowa i jej rozkład

Niech dana będzie przestrzeń probabilistyczna (

Ω

, B, P).

Zmienną losową (ozn. zm. l.) o wartościach rzeczywistych

(ang.

real-valued random variable

) nazywamy funkcję X

określoną na zbiorze

Ω

i przyjmującą wartości rzeczywiste:

X:

Ω

→

R,

spełniającą dla każdego x

∈

R warunek:

{

ω∈Ω

: X(

ω

)

≤

x}

∈

B.

Zm. l. są oznaczane dużymi literami X, Y, W, T, Z, a w razie

potrzeby dodatkowo z indeksami.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

4

Z def. zm. l. wynika, że dla x, x

1

, x

2

∈

R (gdzie x

1

< x

2

)

zdarz. są również zbiory:

{

ω∈Ω

: X(

ω

) < x}, {

ω∈Ω

: X(

ω

)

≥

x}, {

ω∈Ω

: X(

ω

) > x},

{

ω∈Ω

: X(

ω

)

=

x}, {

ω∈Ω

: X(

ω

)

∈

[x

1

, x

2

]},

{

ω∈Ω

: X(

ω

)

∈

[x

1

, x

2

)}, {

ω∈Ω

: X(

ω

)

∈

(x

1

, x

2

]},

{

ω∈Ω

: X(

ω

)

∈

(x

1

, x

2

)}.

Zdarzenia te są oznaczane: X < x, X

≥

x, X > x, X = x, x

1

≤

X

≤

x

2

, x

1

≤

X < x

2

, x

1

< X

≤

x

2

, x

1

< X < x

2

.

Jeżeli zbiór

Ω

jest skończony, to każda funkcja X:

Ω

→

R

jest zm. l.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

5

Przykład 1. Określić zm. l. opisującą wynik badania jakości
pewnej partii wyrobów

Ω

.

Rozwiązanie.

Jako zm. l. wystarczy obrać funkcję przyjmują-

cą dwie wartości, np. 1, jeżeli wylosowany wyrób

ω

okaże się

wadliwy oraz 0, jeżeli okaże się dobry, tj. dla

ω

∈

Ω

:

p.

p.

w

dobrego

wyrobu

dla

,

,

1

0

=

)

(







ω

X

.

Zm. l. X z przykładu 1 nazywa się zm. l. zero-jedynkową.

Tak określona zm. l. może być modelem dowolnego doświad-
czenia dychotomicznego, tj. takiego którego wynik zaliczyć
można jedynie do dwóch wykluczających się kategorii.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

6

Ogólnie, wektor X

=

(X

1

,…, X

n

) taki, że X:

Ω

→

R

n

, tj. dla

i

=

1, 2,…, n, X

i

:

Ω

→

R, nazywamy

wektorem losowym

lub

wielowymiarową zm. l.,

jeżeli

B

R

R

∈

≤

ω

≤

ω

∈

ω

∀

∀

∈

∈

}

)

(

,...,

)

(

:

{

...

1

1

1

n

n

x

x

x

X

x

X

n

Ω

Ω

Ω

Ω

.

Współrzędne X

i

wektora l. nazywamy

zm. l. brzegowymi.

Zbiór

wartości zm. l. X

X(

Ω

)

=

{x

∈

R

n

:

∃

ω∈Ω

x

=

X(

ω

)}

nazywamy jej obrazem.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

7

Niech dana będzie przestrzeń probab. (

Ω

, B, P) oraz okre-

ś

lona na niej rzeczywista zm. l. X. Ponadto niech B(R) będzie

rodziną zbiorów borelowskich na prostej.

Rozkładem prawdop. rzeczywistej zm. l. X nazywamy funk-

cję P

X

określoną wzorem:

∀

A

∈

B(R)

P

X

(A)

=

P{

ω∈Ω

: X(

ω

)

∈

A}.

Funkcja P

X

spełnia aksjomaty Kołmogorowa.

Po wprowadzeniu pojęcia zm. l. w zasadzie nie będziemy

się już zajmować wyjściową przestrzenią probab., a jedynie
przestrzenią probab. indukowaną przez zm. l., czyli przestrze-
nią (R

n

, B(R

n

), P

X

).

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

8

2. Niezależność zmiennych losowych

Rzeczywiste zm. l. X

1

, X

2

,…, X

n

określone na tej samej

przestrzeni (

Ω

, B, P) nazywamy niezależnymi zm. l., gdy dla

każdego ciągu zbiorów borelowskich B

1

, B

2

,…B

n

∏

=

=

∈

ω

∈

ω

=

∈

ω

∈

ω

n

i

i

i

n

i

i

i

B

X

B

X

1

1

}

)

(

:

P{

)}

)

(

(

:

P{

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

I

.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

9

Przykład 2. Określić dwie różne zm. l. Z

1

i Z

2

opisujące wy-

nik zaliczenia przedmiotu i zbadać ich niezależność.

Rozwiązanie.

Zm. l. Z

1

i Z

2

są funkcjami

Z

1

, Z

2

: {A, B, C, D, E, F}

→

R,

które określamy następująco:

Z

1

(A)

=

5;

Z

2

(

ω

)

=

0 dla

ω

∈

{F},

Z

1

(B)

=

4,5;

Z

2

(

ω

)

=

1 dla

ω

∈

Ω

\{F},

Z

1

(C)

=

4;

Z

1

(D)

=

3,5;

Z

1

(E)

=

3;

Z

1

(F)

=

2.

Zm. l. Z

1

jest określona zgodnie z systemem ocen w szkolnic-

twie wyższym, a Z

2

informuje o zaliczeniu przedmiotu.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

10

3. Dystrybuanty, ich własności i zastosowanie

Dystrybuantą

(ang.

cumulative distribution function

(CDF)) zm. l. X nazywamy funkcję rzeczywistą zmiennej rze-
czywistej F

X

: R

→

R, określoną wzorem:

F

X

(x)

=

P(X

≤

x)

=

P{

ω∈Ω

: X(

ω

)

≤

x}.

Uwaga.

Podana definicja dystrybuanty jest zgodna z nor-

mą PN-ISO 3534-1. W literaturze naukowej często dystrybu-
anta jest definiowana wzorem F

X

(x)

=

P(X < x).

Dla dwuwymiarowej zm. l. (X, Y) funkcję F

X,Y

, określoną

dla każdej pary liczb rzeczywistych (x, y) wzorem:

)

,

(

P

)

,

(

)

,

(

,

2

y

Y

x

X

y

x

F

y

x

Y

X

≤

≤

=

∋

a

R

nazywamy

dystrybuantą łączną

(the join CDF.)

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

11

Dystrybuantami

brzegowymi (marginal distribution func-

tion)

zm. l. X i Y nazywamy funkcje F

X

i F

Y

, gdzie

F

X

=

lim

y

→∞

F(x, y), F

Y

=

lim

x

→∞

F(x, y).

Twierdzenie o dystrybuancie

Funkcja F(x) jest dystrybuantą zm. l. o wartościach rzeczywi-
stych wtedy i tylko wtedy, gdy

1. jest funkcją niemalejącą, to znaczy spełnia formułę

∀

(x

1

, x

2

∈

R) (x

1

< x

2

⇒ F(x

1

)

≤

F(x

2

));

2. ma własności graniczne

0

=

)

(

lim

x

F

x

−∞

→

,

1

=

)

(

lim

x

F

x

+∞

→

,

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

12

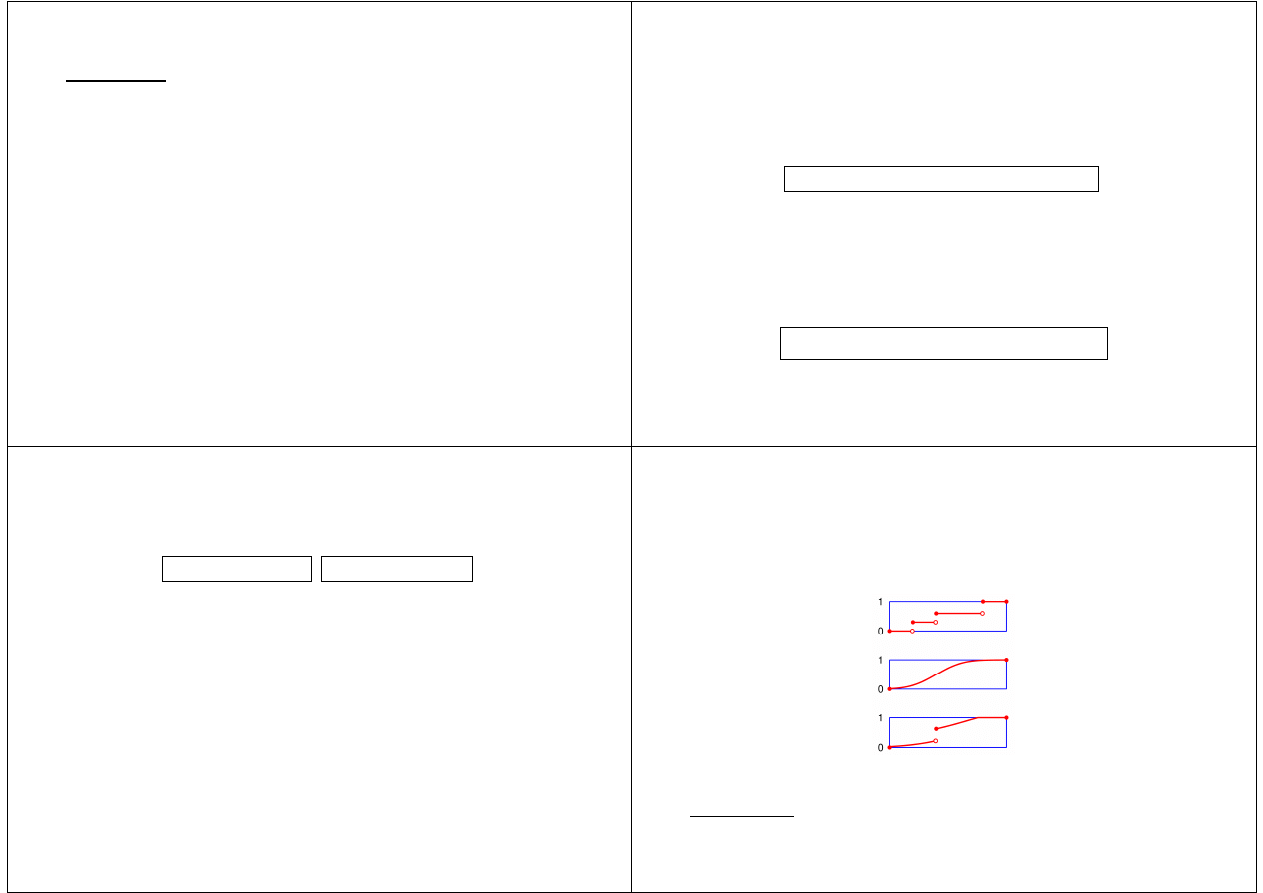
3. jest funkcją co najmniej prawostronnie ciągłą

1

, tj.

∀

x

∈

R,

∀ε

>0,

)

(

)

(

lim

)

(

0

x

F

x

F

x

F

def

=

ε

+

=

+

→

ε

.

Rys. 1. Graficzne przedstawienie własności dystrybuanty

1

Przyjęta co najmniej prawostronna ciągłość jest zgodna z obowiązującą normą PN-ISO 3534-1:2002.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

13

Twierdzenie

(o dystrybuancie niezależnych zm. l.). Zm. l. X

1

,

X

2

,…, X

n

określone na tej samej przestrzeni probabilistycznej,

o wartościach w R są niezależne, wtedy i tylko wtedy, gdy dla
dowolnych x

1

, x

2

…, x

n

∈

R,

∏

=

=

n

i

i

i

n

X

X

X

x

F

x

x

x

F

n

1

2

1

,...,

,

)

(

)

,...,

,

(

2

1

,

gdzie

)

,...,

,

(

2

1

,...,

,

2

1

n

X

X

X

x

x

x

F

n

jest łączną CDF, a

)

(

i

i

x

F

brzego-

wą CDF.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

14

Przykład 3. Niech X

1

, X

2

,…, X

n

będą niezależnymi zm. l. o

dystrybuantach F

1

, F

2

,…, F

n

. Wyznaczyć dystrybuantę zm. l.

a)

Y

=

max(X

1

, X

2

,…, X

n

),

b)

Z

=

min(X

1

, X

2

,…, X

n

).

Rozwiązanie.

Z definicji dystrybuanty i założenia niezależ-

ności zm. l.

a)

F

Y

(x)

=

P(Y

≤

x)

=

P(max(X

1

, X

2

,…, X

n

)

≤

x)

=

P(X

1

≤

x, X

2

≤

x,…, X

n

≤

x)

=

F

1

(x) F

2

(x)…, F

n

(x).

b)

F

Z

(x)

=

P(Z

≤

x)

=

1

−

P(Z > x)

=

1

−

P(X

1

> x, X

2

> x,…,

X

n

> x)

=

1

−

P(X

1

> x) P(X

2

> x)…P(X

n

> x)

=

1

−

(1

−

P(X

1

≤

x)) (1

−

P(X

2

≤

x))…(1

−

P(X

n

≤

x))

=

1

−

Π

i

(1

−

F

i

(x)).

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

15

Przykład 4. Sprawdzić, czy funkcja F zmiennej x z parame-
trem k > 0 określona wzorem:

k

x

k

x

x

x

k

k

x

F

≥

<

≤

<












+

=

0

0

dla

dla

dla

1

7

,

0

1

,

0

0

)

;

(

jest dystrybuantą pewnej zm. l. Sporządzić wykres funkcji F.

Rozwiązanie.

Podana funkcja jest dystrybuantą pewnej zm. l.

ponieważ spełnia wszystkie trzy warunki konieczne i wystar-
czające dla dystrybuanty.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

16

Dystrybuanty mają zastosowanie do obliczania prawdop.

zdarzeń. Dla x, x

1

, x

2

∈

R (x

1

< x

2

) korzystamy z zależności:

1. P(X

=

x)

=

F(x)

−

F(x

−

)

2. P(X < x)

=

F(x

−

),

3. P(X

≤

x)

=

F(x),

4. P(X > x)

=

1

−

F(x),

5. P(X

≥

x)

=

1

−

F(x

−

),

6. P(x

1

< X

≤

x

2

)

=

F(x

2

)

−

F(x

1

),

7. P(x

1

≤

X

≤

x

2

)

=

F(x

2

)

−

F(x

1

−

),

8. P(x

1

< X < x

2

)

=

F(x

2

−

)

−

F(x

1

),

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

17

Przykład 5. Prom kursuje między przystaniami a i b, znajdu-
jącymi się na dwu przeciwległych brzegach rzeki i odległymi
od siebie o k km. Wiadomo, że

P(A)

=

0,1

−

prawd. znajdowania się promu na przystani a,

P(B)

=

0,2

−

prawd. znajdowania się promu na przystani b.

Prom pływa ze stałą prędkością i nie zatrzymuje się na rzece
poza przystaniami. Niech X oznacza odległość promu od
przystani a.

a)

Wyznaczyć dystrybuantę F

X

zm. l. X.

b)

Obliczyć prawdop. zdarzeń:

X

=

0,5k; X

=

0; X

=

k; X > 0,5k;

X

≤

0,01k; 0,4k < X < 0,6k.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

18

Rozwiązanie.

a) Dystrybuanta F

X

jest określona wzorem z

przykładu 4.

b) Prawdop. wskazanych zdarzeń obliczamy z zależności
podanych w punkcie 4:

P(X

=

0,5k)

=

F

X

(0,5k)

−

F

X

(0,5k

−

)

=

0;

P(X

=

0)

=

F(0)

−

F(0

−

)

=

0,1

−

0

=

0,1;

P(X

=

k)

=

F(k)

−

F(k

−

)

=

1

−

0,8

=

0,2;

P(X > 0,5k)

=

1

−

F(0,5k)

=

1

−

(0,1

+

0,35)

=

0,55;

P(X

≤

0,01k)

=

F(0,01k)

=

0,1

+

0,007

=

0,107;

P(0,4k < X < 0,6k)

=

F(0,6k

−

)

−

F(0,4k)

=

(0,1

+

0,42)

−

(0,1

+

0,28)

=

0,14.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

19

Przykład 6. Niech rozkład ocen z zaliczenia przedmiotu bę-
dzie równomierny.

a) Określić dwie różne zm. l. opisujące ocenianie wiedzy.

b) Wyznaczyć dystrybuanty F

1

i F

2

.

c) Czy zm. l. opisujące dwa sposoby oceny wiedzy są nie-

zależne ?

Rozwiązanie.

a) Niech

Ω

=

{A, B, C, D, F}, gdzie zdarzenia

elementarne oznaczają otrzymaną ocenę przez losowo wybra-
nego studenta. Zm. l. Z

1

i Z

2

określamy jak w przykładzie 2.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

20

b) Dystrybuanty zm. l. Z

1

i Z

2

są określone wzorami:































≥

∈

∈

∈

∈

∈

<

=

.

5

),

5

;

5

,

4

[

),

5

,

4

;

4

[

),

4

;

5

,

3

[

),

5

,

3

;

3

[

),

3

;

2

[

,

2

dla

dla

dla

dla

dla

dla

dla

1

6

/

5

6

/

4

6

/

3

6

/

2

6

/

1

0

)

(

1

x

x

x

x

x

x

x

x

F

.

1

),

1

,

0

[

,

0

dla

dla

dla

1

6

/

1

0

)

(

2

≥

∈

<












=

y

y

y

y

F

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

21

c) Sprawdzamy niezależność Z

1

i Z

2

, np. czy

F

1

(3)F

2

(0)

=

F

1,2

(3, 0).

F

1

(3)

=

P(Z

1

≤

3)

=

P{E, F}

=

1/3,

F

2

(0)

=

P(Z

2

≤

0)

=

P{F}

=

1/6,

P(Z

1

≤

3, Z

2

≤

0)

=

P{F}

=

1/6, czyli F

1

(3) F

2

(0)

≠

F

(1, 2)

(3, 0).

Stąd zm. losowe Z

1

i Z

2

nie są niezależne.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

22

4. Zmienna losowa typu dyskretnego

Zm. l. X określoną na (

Ω

, B, P) nazywamy

zm. l.

typu dys-

kretnego

(

discrete R.V.

), jeżeli jej obraz X(

Ω

) jest zbiorem co

najwyżej przeliczalnym.

Dystrybuanta F

X

rzeczywistej zm. l. X jest wówczas funk-

cją przedziałami stałą. Skoki ma tylko w punktach nieciągło-
ś

ci x

1

, x

2

,…, x

n

,….

Skoki w tych punktach mają wartości p

1

, p

2

,…, p

n

,…,

gdzie p

i

=

P(X

=

x

i

) = P{

ω∈Ω

: X(

ω

)

=

x

i

} oraz

Σ

p

i

=

1.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

23

Funkcja prawdopodobieństwa

Niech X:

Ω

→ R będzie zm. l. typu dyskretnego.

Funkcją prawdopodobieństwa (probability mass function

PMF) nazywamy funkcję f

X

: R → [0, 1] taką, że

f

X

(x)

=

P(X

=

x)

=

P{

ω∈Ω

: X(

ω

)

=

x}.

Jeżeli X(

Ω

)

=

{x

1

, x

2

, ... } oraz f

X

(x

k

)

=

p

k

, to PMF zwykle

jest podawana w postaci

















=

...

...

3

2

1

3

2

1

p

p

p

x

x

x

f

X

.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

24

Dla wektora l. (X, Y) z obrazami X(

Ω

)

⊆

R i Y(

Ω

)

⊆

R,

możemy rozważać zdarzenia dla każdej pary ich wartości
(x

i

, y

j

), gdzie x

i

,

∈

X(

Ω

), y

j

∈

Y(

Ω

), tj.

{

ω∈Ω

: X(

ω

)

=

x

i

, Y(

ω

)

=

y

j

} (krótko {X

=

x

i

, Y

=

y

j

}).

Prawdop. P(X

=

x

i

, Y

=

y

j

) określa łączny rozkład pary (X, Y).

Funkcję f

X,Y

: R

2

→ [0, 1] określoną wzorem

f

X,Y

(x

i

, y

j

)

=

P(X

=

x

i

, Y

=

y

j

) ,

nazywamy

łączną funkcją prawdop

. (the join PMF) dla pary

X i Y.

Brzegowe f. prawdop. (“marginal” PMFs) P(X

=

x

i

) i P(Y

=

y

j

) otrzymujemy poprzez sumowanie po wszystkich warto-

ś

ciach pozostałej zm. l., tj.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

25

P(X

=

x

i

)

=

Σ

j

P(X

=

x

i

, Y

=

y

j

),

P(Y

=

y

j

)

=

Σ

i

P(X

=

x

i

, Y

=

y

j

).

Elementy p

ij

łącznej funkcji prawdop. zwykle umieszczamy w

tablicy dwudzielczej.

Tablica 1.

Schemat tablicy dwudzielczej

X \ Y y

1

y

2

... y

m

f

X

x

1

p

11

p

12

... p

1m

p

1

•

x

2

p

21

p

22

... p

2m

p

2

•

...

... ... ... ... …

x

n

p

n1

p

n2

... p

nm

p

n

•

f

Y

p

•

1

p

•

2

... p

•

m

1

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

26

Twierdzenie

(o funkcji prawdop. niezależnych zm. l.). Zm. l.

X

1

, X

2

,…, X

n

o rozkładach typu dyskretnego są niezależne

wtedy i tylko wtedy, gdy dla każdego ciągu x

1

, x

2

,…, x

n

war-

tości zm. l-wych.

P(X

1

=

x

1

, X

2

=

x

2

,…, X

n

=

x

n

)

=

Π

i

P(X

i

=

x

i

) .

Przykład 7. (Palenie i rak). W grupie 60 osób, liczby tych
którzy palą lub nie palą i mają lub nie mają raka są zebrane w
tablicy 1. Niech

Ω

będzie zbiorem zdarzeń elementarnych do-

tyczących tej grupy. Z grupy tej losujemy jedną osobę. Niech
C(

ω

)

=

1, jeśli osoba ta ma raka i 0 jeśli nie ma raka oraz

niech S(

ω

)

=

1, jeśli osoba ta pali papierosy i 0 w p.p.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

27

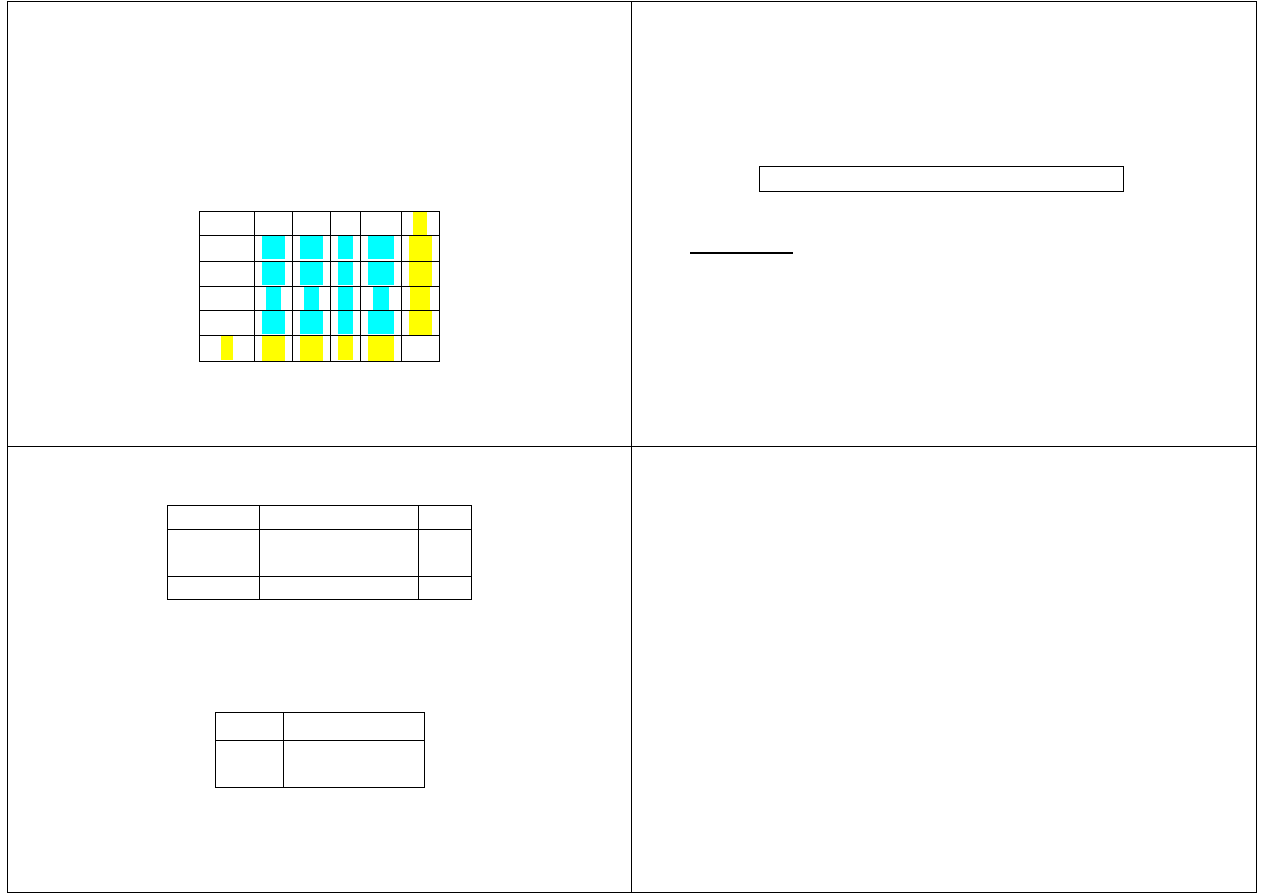
C\S

nie pali pali suma

bez raka
z rakiem

40 10
7 3

50
10

suma

47 13

60

Tablica 1. Palenie i rak

Łączny rozkład (C, S) jest dany w tablicy 2. Na przykład

P(C

=

0; S

=

0)

=

40/60, P(C

=

0, S

=

1)

=

10/60, i tak dalej.

C\S

0 1

0
1

40/60 10/60

7/60 3/60

Tablica 2. Łączny rozkład.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

28

Stąd rozkłady brzegowe zm. l. C i S:















=

60

/

13

60

/

47

1

0

S

f

,















=

60

/

10

60

/

50

1

0

C

f

.

Zm. l. S i C nie są niezależne, ponieważ

P(C

=

1, S

=

1)

=

3/60

=

0,05,

a P(C

=

1) P(S

=

1)

=

0,036.

Zm. l. typu dyskretnego są modelami pomiarów w słabych

skalach. Modele jakościowego odbioru partii produktów, oce-
ny zaliczeniowej, czy rzutu kostką są przykładami takich zm.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

29

Związek pomiędzy dystrybuantą a funkcją prawd.

Dystrybuanta F zm. l. typu dyskretnego, w punkcie x

∈

R,

jest związana z funkcją prawd. równością:

∑

≤

=

x

x

i

i

x

f

x

F

)

(

)

(

.

Stąd w punktach skokowych x

i

otrzymujemy:

)

(

)

(

)

(

1

−

−

=

i

i

i

x

F

x

F

x

f

.

Rozkład zm. l. typu dyskretnego charakteryzują: funkcja

prawd. i dystrybuanta F. Gdy znana jest jedna z tych funkcji,
można wyznaczyć drugą z nich.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

30

5. Warunkowe zmienne losowe i ciągi niezależnych

prób

Niech na przestrzeni probabilistycznej (

Ω

, B, P) określona

będzie para (X, Y) rzeczywistych zm. l. typu dyskretnego.

Jeżeli wiadomo, jaką wartość przyjęła zm. l. Y, to warunko-

we prawdop. zm. l. X jest określone wzorem:

)

(

P

)

,

(

P

)

(

P

j

j

i

j

i

y

Y

y

Y

x

X

y

Y

x

X

=

=

=

=

=

=

.

Warunkowe prawdopodobieństwo można uogólnić na ciąg
zm. l. X

1

,…, X

n

.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

31

Przykład 8 (kontynuacja przykładu 7). Z badanej grupy 60
osób wylosowano osobę, która miała raka. Jakie jest praw-
dop., że była palaczem?

Rozwiązanie.

Dopasowując oznaczenia do wzoru na

prawdop. warunkowe otrzymujemy

3

,

0

60

/

10

60

/

3

)

1

(

P

)

1

,

1

(

P

)

1

1

(

P

=

=

=

=

=

=

=

=

C

C

S

C

S

.

W zastosowaniach szczególną rolę odgrywają ciągi X

1

, X

2

,

. . . , X

n

niezależnych zm. l. o tym samym rozkładzie (i.i.d. in-

dependent and identically distributed), zwane w statystyce
matematycznej

niezależnymi próbami

.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

32

W praktyce statystycznej ciągi niezależnych prób występu-

ją w naturalny sposób. Na przykład eksperyment polega na
obserwacji wartości W

=

{x

1

, x

2

,…, x

s

} zm. l. X o nieznanej

funkcji prawdop. PMF

















=

s

s

X

p

p

p

x

x

x

f

...

...

2

1

2

1

.

Eksperyment powtarzamy niezależnie n razy. Do opisania
ciągu prób wybieramy zbiór W

=

W

n

zwany przestrzenią prób

(sample space), zawierający wszystkie możliwe ciągi warto-
ś

ci x

=

(x

1

, x

2

,…, x

n

), gdzie x

i

∈

W dla i

=

1, 2,…, n. Wówczas

zm. l. X

1

, X

2

, . . . , X

n

opisujące wyniki poszczególnych prób

tworzą ciąg i.i.d. zm. l.

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

33

Twierdzenie

(o dystrybuancie próby prostej). Jeżeli X

1

, X

2

,…,

X

n

jest ciągiem zm. l. i.i.d. o dystrybuancie F, to dla wszyst-

kich x

1

, x

2

…, x

n

∈

R,

∏

=

=

n

i

i

n

X

X

X

x

F

x

x

x

F

n

1

2

1

,...,

,

)

(

)

,...,

,

(

2

1

,

Przykład 9. Doświadczenie polega na trzykrotnym rzucie
prawidłową kostką. Niech X

i

reprezentuje wynik rzutu na i-tej

kostce, dla i

=

1, 2, 3.

a)

Wyznaczyć wspólną PMF.

b)

Wyznaczyć przestrzeń prób i PMF dla niej.

c)

Obliczyć prawdop. otrzymania za każdym razem
parzystej liczby oczek

K. J. Andrzejczak, MPiS30 W04: Zmienne losowe I

34

a) Wspólną funkcją prawdop. jest















=

6

/

1

6

6

/

1

5

6

/

1

4

6

/

1

3

6

/

1

2

6

/

1

1

X

f

b) Przestrzenią prób jest W

====

W

×

W

×

W, gdzie W

=

{1, 2,

3, 4, 5, 6}. Jeżeli x

=

(1, 3, 6), to X

1

=

1, X

2

=

3 i X

3

=

6.

Prawdop. dla każdego x

=

(x

1

, x

2

, x

3

) wynosi

P(X

=

(x

1

, x

2

, x

3

))

=

1/216.

c) Prawdop. otrzymania parzystej liczby oczek w jednej
próbie wynosi ½. Trzy próby są niezależne, więc szukane
prawdop. wynosi 1/8.