K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

1

MPiS30 W06: CHARAKTERYSTYKI

LICZBOWE ZMIENNEJ LOSOWEJ

1.

Charakterystyki liczbowe zmiennej losowej

2.

Charakterystyki położenia

Przykład 1
Przykład 2
Przykład 3

3.

Charakterystyki rozrzutu

Przykład 4
Przykład 5

4.

Momenty zwykłe i centralne

Przykład 6

5.

Charakterystyki asymetrii i spłaszczenia

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

2

6.

Charakterystyki współzależności liniowej

Przykład 7
Przykład 8

7.

Zmienna losowa standaryzowana i jej własności

8.

Nierówność Czebyszewa

Przykład 9

9.

Nierówność Gaussa

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

3

1. Charakterystyki liczbowe zm. l.

Niech

na (

Ω

, B, P) określone będą zm. l. X

1

,…, X

n

o war-

tościach rzeczywistych.

Charakterystykami liczbowymi

zm.

l.-ych (lub ich rozkładów prawdop.) nazywamy liczby charak-
teryzujące zbiór wartości, jakie mogą one przyjmować, np.
pod względem wartości najbardziej prawdop., rozrzutu wokół
pewnej wartości, kształtu wykresu funkcji prawdop. lub
krzywej gęstości, a w przypadku kilku zm. l. współzależności
między nimi.

Charakterystyka liczbowa służy do syntetycznego opisu

wartości zm. l. Za pomocą kilku liczb można uzyskać w pro-
sty sposób dostatecznie dobre informacje o rozkładzie zm. l.
lub zależnościach pomiędzy zm. l.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

4

2. Charakterystyki położenia

Charakterystykę liczbową zm. l. X nazywamy

charaktery-

styką położenia

, jeśli dodanie do zm. l. dowolnej stałej zmie-

nia wartość tej charakterystyki o tę stałą.

Do podstawowych charakterystyk położenia wartości zm.

l. należą:

a)

wartość oczekiwana

(ang. mean),

b)

wartość modalna

(ang. mode)

c)

kwartyle

(ang. quartile).

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

5

Wartością oczekiwaną

(wartością średnią, ang. expected va-

lue, mean) zm. l. X nazywamy liczbę m

X

=

E(X), przy czym

a)

dla zm. l. typu dyskretnego

E(X)

=

∑ x

i

p

i

b)

dla zm. l. typu ciągłego

∫

+∞

∞

−

=

dx

x

xf

X

)

(

)

(

E

przy założeniu, że występujący szereg i całka są bezwzględ-
nie zbieżne. W przeciwnym przypadku powiemy, że zm. l. nie
ma wartości oczekiwanej.

Mianem wartości oczekiwanej jest miano badanej zm. l.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

6

Przykład 1. Rozkład zm. l. T jest określony za pomocą PMF:

f(t)

=

P(T

=

t)

=

q

t

−

1

p, t

=

1, 2,…

Wyznaczyć wartość oczekiwaną zm. l. T.

Rozwiązanie. Z definicji wartości oczekiwanej

E(T)

=

1 p

+

2qp

+

3q

2

p

+

…

=

p(1

+

2q

+

3q

2

+

…).

Korzystamy z faktu, że jeśli x < 1, to

1

+

x

+

x

2

+

x

3

+

…..

=

1/(1

−

x).

Różniczkując tę formułę, otrzymujemy

1

+

2x

+

3x

2

+

…

=

1/(1

−

x)

2

, więc

E(T)

=

p/(1

−

q)

2

=

p /p

2

=

1/p.

Jeśli doświadczenie polega na rzucaniu prawidłową monetą,
to oczekiwana liczba rzutów do otrzymanie po raz pierwszy

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

7

orła wynosi 2. Jeżeli rzucamy kostką, to oczekiwana liczba
rzutów do otrzymania po raz pierwszy szóstki wynosi 6.

Własności wartości oczekiwanej

Niech na przestrzeni (

Ω

, B, P) określone będą dwie zm. l. X i

Y dla których istnieją wartości oczekiwane oraz niech a, b, c

∈

R. Wówczas

1.

E(c)

=

c;

2.

E(aX)

=

aE(X);

3.

E(X

+

b)

=

E(X)

+

b;

4.

E(X

+

Y)

=

E(X)

+

E(Y).

5.

Jeżeli zm. l. X i Y są niezależne, to

E((X

−

EX)(Y

−

EY))

=

0.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

8

Z własności 2, 3 i 4 wynika, że operator E jest operatorem li-
niowym. Własność 4 można uogólnić na przypadek skończo-
nej sumy zm. l.

Jeżeli zm. l. X i Y spełniają warunek z tezy własności 5, to

nazywamy je

nieskorelowanymi zm. l.

Jeżeli zm. l. X ma wartość oczekiwaną m, to zm. l.

Y

=

X

−

m

nazywamy zm. l. scentrowaną

.

Przykład 2. Niech X będzie liczbą punktów stałych w loso-
wej permutacji zbioru {a, b, c}.

a) Wyznaczyć wartość oczekiwaną zm. l. X.
b) Uogólnić wynik na zbiór n elementowy.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

9

Rozwiązanie.

a) Doświadczenie jest tu określone poprzez

permutację zbioru {a, b, c}. Stąd zbiór zdarzeń elementarnych

Ω

=

{(a, b, c), (a, c, b), (b, a, c), (b, c, a), (c, a, b), (c, b, a)}.

Każdy wynik zachodzi z prawdop. 1/6. Liczby punktów sta-
łych podane są w tablicy 1.1.

Ω

X

p

i

a b c
a c b
b a c
b c a
c a b
c b a

3
1
1
0
0
1

1/6
1/6
1/6
1/6
1/6
1/6

Tablica 1.1. Liczby punktów stałych.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

10

Obliczamy E(X ) zm .l . typu dyskretnego

1

6

1

1

6

1

0

6

1

0

6

1

1

6

1

1

6

1

3

=













+













+













+













+













+













.

b) Wyznaczymy oczekiwaną liczbę punktów stałych w loso-
wej permutacji zbioru {1, 2, 3,…, n}. Dla każdego i, 1

≤

i

≤

n,

niech X

i

(

ω

) równa się 1, jeśli losowa permutacja

ω

ma punkt

stały na i-tym miejscu, i 0 w p. p. Dla każdego i,

E(X

i

)

=

1/n.

Niech Y oznacza liczbę punktów stałych w permutacji

ω

Y(

ω

)

=

X

1

(

ω

)

+

X

2

(

ω

)

+

…

+

X

n

(

ω

).

Z własności liniowości dla n zm. l. wynika, że

E(Y)

=

E(X

1

)

+

E(X

2

)

+

…

+

E(X

n

), stąd E(Y)

=

1.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

11

Przykład 3. Niech X

i

, i

=

1, 2,…, n będą i.i.d. zm. l. o rozkła-

dzie jednostajnym na [0, 1] oraz Y

n

=

max{X

1

,…, X

n

}.

a)

Wyznaczyć E(Y

n

)).

b)

Wyznacz funkcję kwantylową i kwantyl rzędu 0,9 zm. l.
Y

n

.

Rozwiązanie.

Z założenia o jednostajności rozkładu zm. l. X

i

.

1

,

1

0

,

0

dla

dla

dla

,

1

,

,

0

)

(

,...

2

,

1

≥

<

≤

<












=

∀

=

x

x

x

x

x

F

i

X

n

i

Z definicji zm. l. Y

n

i niezależności zm. l. X

i

mamy

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

12

)

,...,

(

P

)

}

,...,

(max{

P

)

(

1

1

x

X

x

X

x

X

X

x

F

n

n

Y

n

≤

≤

=

≤

=

)

(

...

)

(

)

(

P

...

)

(

P

1

1

x

F

x

F

x

X

x

X

n

X

X

n

⋅

⋅

=

≤

⋅

⋅

≤

=

.

Stąd dystrybuanta i gęstość zm. l. Y

n

dla n

=

1, 2,…

.

1

,

1

0

,

0

dla

dla

dla

,

1

,

,

0

)

(

≥

<

≤

<












=

x

x

x

x

x

F

n

Y

n









<

≤

=

−

,

1

0

.

.p

p

w

dla

,

0

,

)

(

1

x

nx

x

f

n

Y

n

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

13

a) Wyznaczamy wartość oczekiwaną zm. l. Y

n

1

)

(

E

1

0

+

=

=

∫

n

n

dx

x

n

Y

n

n

.

b) Wyznaczamy funkcję kwantylową zm. l. Y

n

dla x

∈

(0, 1).

Ponieważ

p

x

n

p

=

,

więc

n

p

p

x

=

.

Stąd kwantyl rzędu 0,9

n

x

9

,

0

9

,

0

=

.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

14

Wartością modalną

lub

modą

mo(X) (ang. modal value,

mode) zm. l. X nazywamy:
1.

dla zm. l. typu dyskretnego

−

wartość x

k

, odpowiadająca

lokalnemu maksimum funkcji prawdop., tj. wartość różną
od min {x

i

} i max{x

i

}, dla której prawdop. f (x

k

) jest większe

od wartości prawdop. odpowiadających punktom skokowym
leżącym w bezp. sąsiedztwie punktu x

k

.

2.

dla zm. l. typu ciągłego

−

wartość x

0

, w której gęstość f (x)

osiąga maksimum lokalne.

Jeżeli istnieje jedna moda, to rozkład zm. l. X nazywamy

rozkł. jednomodalnym

(unimodal distribution). Jeżeli istnieje

więcej niż jedna moda, wtedy rozkład nazywamy

rozkł. wie-

lomodalnym

(multimodal distribution).

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

15

3. Charakterystyki rozrzutu

Charakterystykę liczbową zm. l. nazywamy

charaktery-

styką rozrzutu

, jeśli dodanie do zm. l. dowolnej stałej nie

zmienia wartości tej charakterystyki. Charakterystykami roz-
rzutu wartości zm. l. są:

a)

wariancja

(ang. variance),

b)

odchylenie standardowe

(ang. standard deviation),

c)

odchylenie ćwiartkowe

.

Względną charakterystyką rozrzutu jest

współczynnik

zmienności

(ang. coefficient of variation).

Niech

X będzie zm. l. określoną na (

Ω

, B, P) i ma wartość

oczekiwaną m

X

=

E(X).

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

16

Wariancją

(variance)

zm. l. X nazywamy wartość oczeki-

waną kwadratu scentrowanej zm. l., tj. liczbę

)

(

D

2

2

X

X

=

σ

określoną wzorem:

D

2

(X)

=

E(X

−

m

X

)

2

,

przy czym

a)

dla zm. l. typu dyskretnego

(

)

∑

−

=

)

(

)

(

D

2

2

i

X

i

x

f

m

x

X

b)

dla zm. l. typu ciągłego

∫

∞

∞

−

−

=

dx

x

f

m

x

X

X

)

(

)

(

)

(

D

2

2

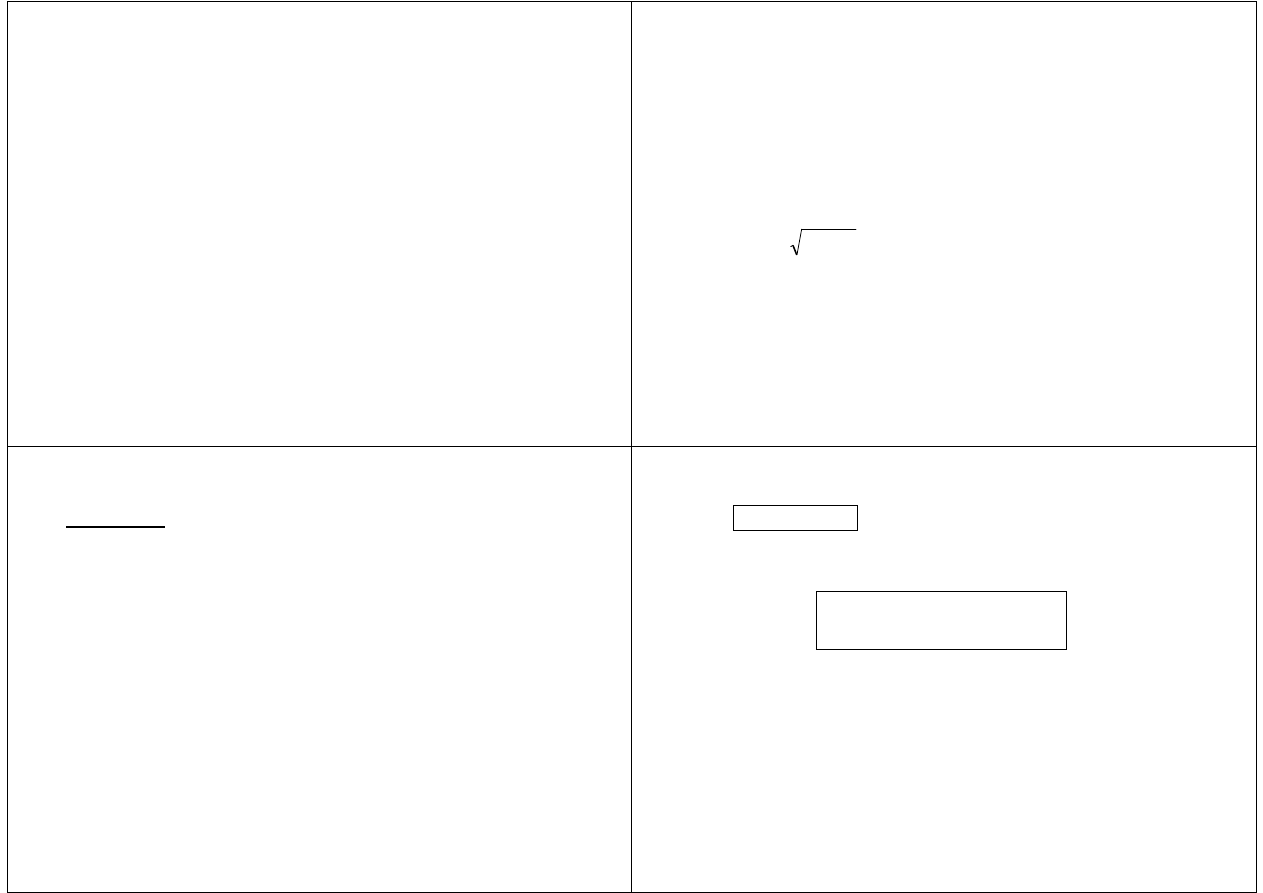
K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

17

Wariancja zm. l. istnieje, gdy szereg (całka) występujący
w definicji wariancji jest zbieżny. Mianem wariancji jest kwa-
drat miana badanej zm. l.

Niech na (

Ω

, B, P) określone będą zm. l. X i Y o skończo-

nych wariancjach oraz a, b

∈

R. Wówczas

a)

D

2

(a)

=

0

−

wariancja stałej zm. l. jest równa zero,

b)

D

2

(X

+

a)

=

D

2

(X)

−

niezmienniczość na przesunięcie,

c)

D

2

(aX)

=

a

2

D

2

(X) dla a

≠

0;

Dowód.

Z def. wariancji i własności wartości oczekiwanej

D

2

(aX)

=

E(aX

−

E(aX))

2

=

E(aX

−

a E(X))

2

=

a

2

D

2

(X).

d)

D

2

(X

+

Y)

=

D

2

(X)

+

D

2

(Y)

+

2 E((X

−

EX)(Y

−

EY)).

Dowód.

Wynika z następujących przekształceń

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

18

D

2

(X

+

Y)

=

E((X

+

Y)

−

E(X

+

Y))

2

=

E((X

−

EX)

+

(Y

−

EY))

2

=

E(X

−

EX)

2

+

E(Y

−

EY)

2

+

2 E((X

−

EX)(Y

−

EY)).

W szczególności, jeśli zm. l. są nieskorelowane, to warian-
cja ich sumy jest równa sumie ich wariancji.

Odchyleniem standardowym

(standard deviation) lub dysper-

sją zm. l. X nazywamy dodatni pierwiastek z wariancji, tj.

liczbę

)

(

D

2

X

X

=

σ

.

Mianem dyspersji jest miano zmiennej X.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

19

Przykład 4. Wkładamy losowo n listów do n zaadresowanych
kopert, przeznaczonych dla różnych adresatów. Wyznaczyć
wartość oczekiwaną i wariancję liczby listów włożonych
prawidłowo.

Rozwiązanie.

Niech X

i

, i

=

1, 2,…, n będzie zm. l. informują-

cą, czy i-ty list został dobrze włożony, tj. niech X

i

=

1, jeśli i-

ty list został włożony prawidłowo oraz X

i

=

0 w przeciwnym

razie.

Ponadto niech X

=

∑

i

X

i

, tj. zm. l. X zlicza listy włożone

prawidłowo do kopert.

Ponieważ P(X

i

=

1)

=

1/n, więc EX

=

1.

W celu wyznaczenia wariancji sumy zm. l. wyprowadza-

my wzór

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

20

D

2

(X

1

+

…

+

X

n

)

=

E(X

1

+

…

+

X

n

)

2

−

(EX

1

+

…

+

EX

n

)

2

(

)

∑

∑

=

≤

<

≤

−

+

−

=

n

i

n

j

i

j

i

j

i

i

i

X

X

X

X

X

X

1

1

2

2

)

E

E

)

(

E

(

2

)

E

(

E

∑

∑

≤

<

≤

=

+

=

n

j

i

j

i

n

i

i

X

X

X

1

1

2

)

,

cov(

2

D

.

Ponieważ

∀

i

=

1,…, n

D

2

X

i

=

(n

−

1)/n

2

,

więc

∑

i

D

2

X

i

=

(n

−

1)/n.

Dla i

≠

j mamy E(X

i

X

j

)

=

P(X

i

X

j

=

1)

=

1/(n(n

−

1)) i każda z

n

2

−

n kowariancji cov(X

i

, X

j

)

=

1/(n

2

(n

−

1)).

Ich suma wynosi 1/n, więc ostatecznie otrzymujemy D

2

X

=

1.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

21

Odchyleniem ćwiartkowym

zm. l. nazywamy charakterystykę

Q

=

(x

0,75

−

x

0,25

)/2,

gdzie x

0,25

, x

0,75

są kwartylami dolnym i górnym.

Współczynnikiem zmienności

(coefficient of variation) zm. l.

X nazywamy iloraz

X

X

m

X

σ

=

ν

(dla m

X

≠

0)

W normie PN-ISO 3534-1 współ. zmienności jest określo-

ny tylko dla nieujemnej zm. l. Współ. zmienności jest liczbo-
wą charakterystyką względnego rozrzutu wartości zm. l. Mo-
ż

e być on wyrażony procentowo.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

22

Praktyczne zastosowanie współ. zmienności wynika z te-

go, że jest charakterystyką bez miana oraz z następującej wła-
sności.

Własność.

Niech X będzie zm. l. taką, że m

X

≠

0. Dla do-

wolnej stałej c

≠

0 prawdziwa jest równość

ν

cX

=

ν

X

.

Dowód.

Z definicji współczynnika zmienności

cX

cX

cX

m

v

/

σ

=

.

Z własności wartości oczekiwanej oraz wariancji

X

X

X

cX

cm

c

ν

=

σ

=

ν

)

/(

)

(

, cnd.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

23

Przykład 5.

Wzrost ludzi z pewnej populacji jest zm. l. X o

wartości oczekiwanej m

X

=

175 [cm] i odchyleniu standardo-

wym

σ

X

=

10 [cm], zaś waga ludzi z tej populacji

−

zm. l. Y

dla której m

Y

=

75 [kg] i

σ

Y

=

5 [kg]. Ze względu, na którą ce-

chę badana populacja ludzi jest bardziej zróżnicowana ?

Rozwiązanie.

Wystarczy porównać współczynniki zmienno-

ś

ci dla obydwu zm. l.. Ponieważ

ν

X

=

2/35,

ν

Y

=

2/30, więc

ν

X

<

ν

Y

, stąd badana populacja ludzi jest bardziej zróżnicowana

ze względu na wagę niż na wzrost.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

24

4. Momenty zwykłe i centralne

Momentem zwykłym

r

−

tego rzędu (r jest liczbą naturalną)

zm. l. X nazywamy charakterystykę liczbową określoną wzo-
rem:

m

r

(X)

=

E(X

r

)

Z istnienia momentów wyższych rzędów wynika istnienie

momentów niższych rzędów. Wartość oczekiwana jest mo-
mentem zwykłym rzędu pierwszego.

Związek między wariancją a momentami zwykłymi

Jeżeli istnieje wariancja D

2

(X) zm. l. X, to

)

(

)

(

)

(

D

2

1

2

2

X

m

X

m

X

−

=

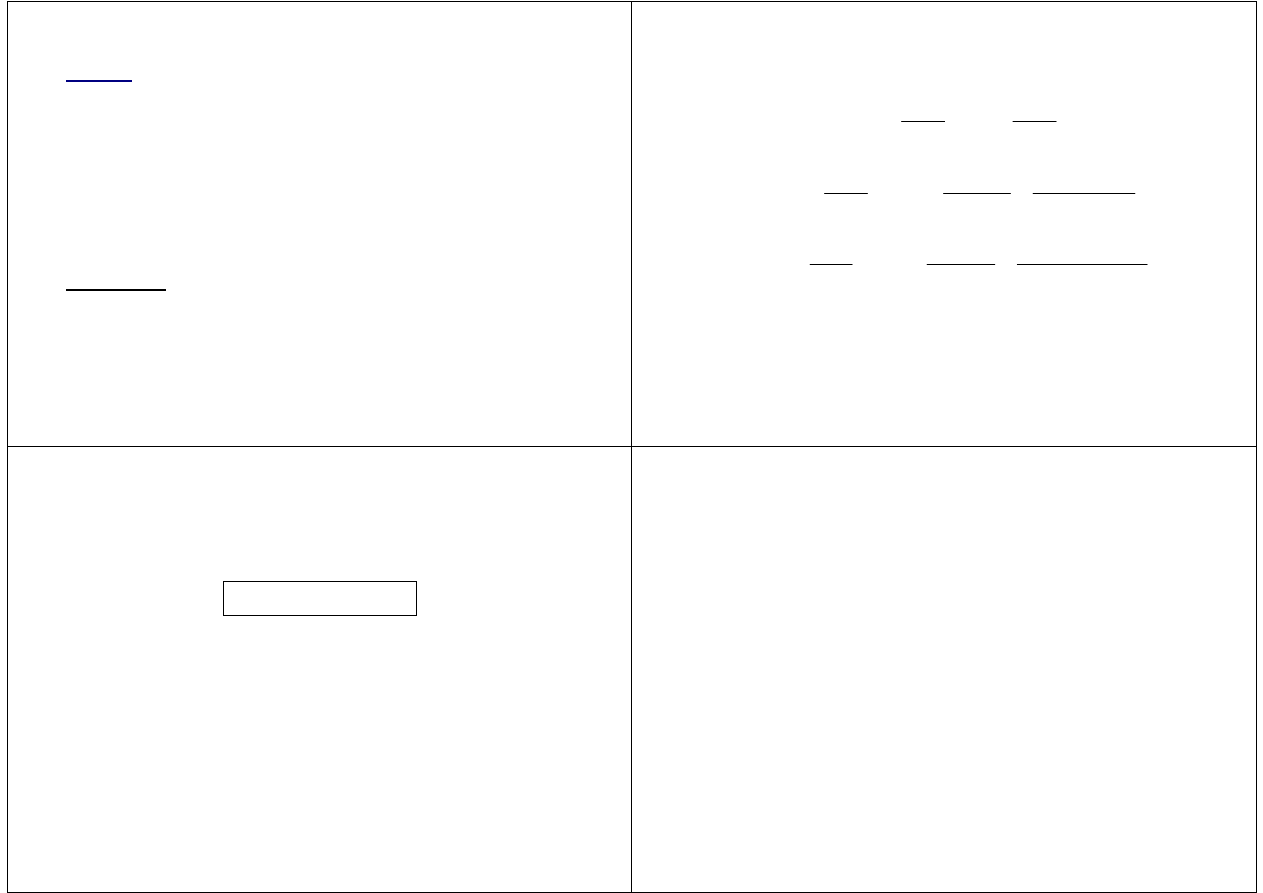
K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

25

Dowód.

Z definicji wariancji

(

)

2

2

)

E

(

E

)

(

D

X

X

X

−

=

(

)

(

)

2

2

)

(

E

)

(

E

2

E

X

X

X

X

+

−

=

.

Z własności wartości oczekiwanej

(

)

2

2

2

)

(

E

)

(

E

)

(

E

2

)

(

E

)

(

D

X

X

X

X

X

+

−

=

(

)

2

1

2

2

2

)

(

E

)

(

E

m

m

X

X

−

=

−

=

.

Przykład 6. Losujemy liczbę z przedziału (a, b), gdzie a < b.
Niech X oznacza wylosowaną liczbę. Wyznaczyć:

a) trzy pierwsze momenty zwykłe;
b) wariancję zm. l. X.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

26

Rozwiązanie.

a) Momenty wyznaczamy przez całkowanie

2

1

)

(

1

b

a

xdx

a

b

X

m

b

a

+

=

−

=

∫

,

3

)

(

3

1

)

(

2

2

3

3

2

2

b

ab

a

a

b

a

b

dx

x

a

b

X

m

b

a

+

+

=

−

−

=

−

=

∫

,

4

)

)(

(

)

(

4

1

)

(

4

2

4

4

3

3

b

a

b

a

a

b

a

b

dx

x

a

b

X

m

b

a

+

+

=

−

−

=

−

=

∫

.

b) Wariancję wyznaczamy ze związku z momentami zwy-
kłymi

12

/

)

(

)

(

D

2

2

1

2

2

a

b

m

m

X

−

=

−

=

,

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

27

Momentem centralnym

k-tego rzędu (k

=

1, 2,…) (

central

moment of order k

) zm. l. X nazywamy wartość oczekiwaną k-

tej potęgi scentrowanej zm. l., tj.

k

k

X

X

X

)

E

(

E

)

(

−

=

µ

Wariancja jest momentem centralnym rzędu drugiego.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

28

5. Charakterystyki asymetrii i spłaszczenia

Charakterystykę liczbową zm. l. X nazywamy

charaktery-

styką asymetrii

, jeśli informuje ona o odchyleniu się jej roz-

kładu od rozkładu symetrycznego. Zm. l. X ma

rozkład syme-

tryczny

, jeśli istnieje taka liczba a, że:

•

w przypadku zm. l. typu dyskretnego każdemu punktowi
skokowemu x

i

≤

a, odpowiada punkt x

j

≥

a taki, że

P(X

=

x

i

)

=

P(X

=

x

j

) oraz a

−

x

i

=

x

j

−

a;

•

w przypadku zm. l. typu ciągłego o gęstości f(x) dla każ-
dego x w punktach ciągłości

f(a

−

x)

=

f(a

+

x).

Liczba a nosi nazwę

liczby centralnej

.

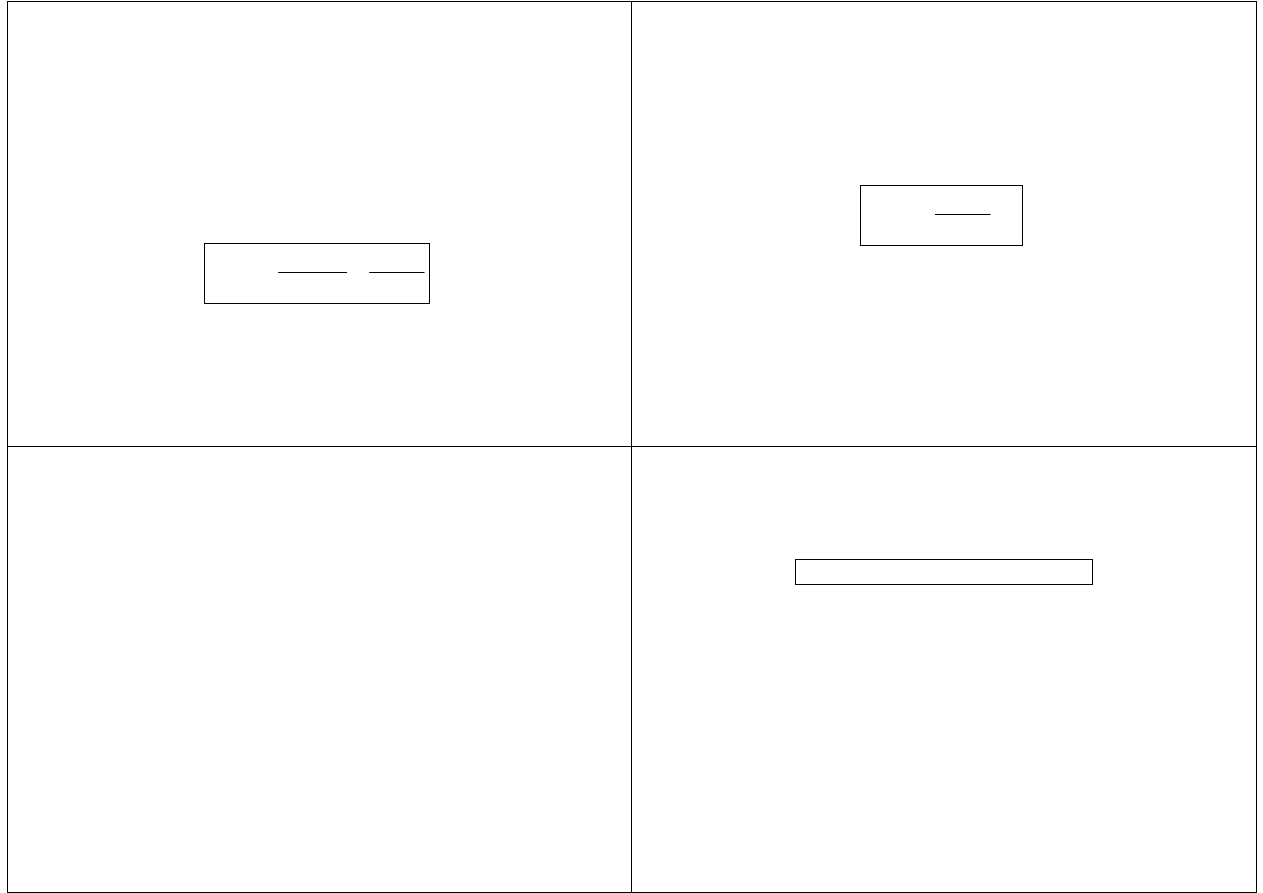
K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

29

Prosta o równaniu x

=

a jest

osią symetrii

wykresu funkcji

prawdop. lub krzywej gęstości.

Rozkład, który nie jest symetryczny nazywamy

rozkładem

asymetrycznym

.

Charakterystyką asymetrii jest

współczynnik asymetrii

.

Współczynnikiem asymetrii

lub

skośnością

(

skewness

)

γ

1

(X) rozkładu zm. l. X nazywamy iloraz

3

3

2

/

3
2

3

1

)

(

)

(

)

(

)

(

X

X

X

X

X

σ

µ

=

µ

µ

=

γ

,

gdzie

µ

2

,

µ

3

i

σ

oznaczają odpowiednio moment centralny

rzędu drugiego, moment centralny rzędu trzeciego i odchyle-
nie standardowe rozkładu zm. l. X.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

30

Współczynnik asymetrii jest miarą odchylenia od symetrii

rozkładu. Dla rozkładów symetrycznych wszystkie momenty
centralne rzędów nieparzystych są równe zeru.

Współczynnikiem spłaszczenia

(ekscesem, ang. excess)

rozkładu zm. l. X nazywamy charakterystykę

3

)

(

)

(

)

(

2
2

4

2

−

µ

µ

=

γ

X

X

X

,

gdzie

µ

2

i

µ

4

oznaczają momenty centralne, odpowiednio rzę-

du drugiego i czwartego, rozkładu zm. l. X.

Współczynnik spłaszczenia jest miarą rozbieżności danego

rozkładu od rozkładu normalnego o tej samej wartości ocze-
kiwanej i wariancji.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

31

6. Charakterystyki współzależności liniowej

Jeżeli rozważamy kilka zm. l. określonych na tej samej

przestrzeni (

Ω

, B, P), to możemy badać je nie tylko z osobna,

ale również współzależności między nimi.

W szczególności, charakterystykami określającymi współ-

zależność liniową pomiędzy parą zm. l. są:

a) kowariancja,

b) współczynnik korelacji.

Niech na (

Ω

, B, P) określone będą zm. l. X

1

, X

2

,…, X

n

o

wartościach rzeczywistych.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

32

Kowariancją zm. l. X

i

i X

j

(i, j

=

1, 2, …, n) spełniających

warunek EX

i

X

j

<

∞

, nazywamy wielkość

cov(X

i

, X

j

)

=

E((X

i

−

EX

i

) ( X

j

−

EX

j

))

Mianem kowariancji jest iloczyn mian badanych zmiennych.

Własności kowariancji:

1) cov(X

i

, X

j

)

=

cov(X

j

, X

i

),

2) cov(X

i

, X

i

)

=

D

2

(X

i

),

3) cov(X

i

, X

j

)

=

E(X

i

X

j

)

−−−−

E(X

i

) E(X

j

),

4)



cov(X

i

, X

j

)

≤

D(X

i

) D(X

j

) – nierówność Schwarza.

Dowód wł. 3.

Z definicji kowariancji i własności wartości

oczekiwanej

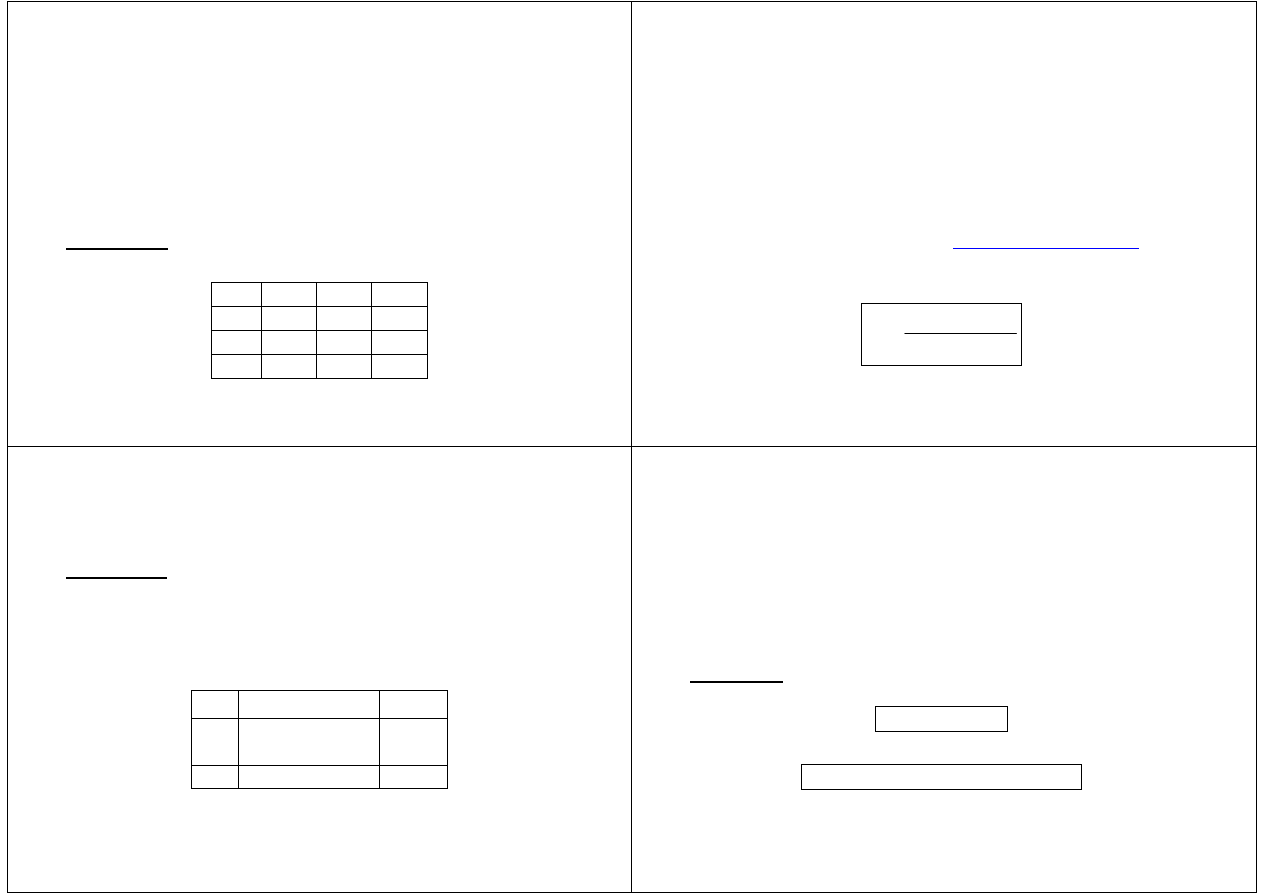
K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

33

cov(X

i

, X

j

)

=

E(X

i

X

j

−

X

j

E(X

i

)

−

X

i

E(X

j

)

+

E(X

i

)E(X

j

))

=

E(X

i

X

j

)

−−−−

E(X

i

)E(X

j

)

−−−−

E(X

i

)E(X

j

)

+

E(X

i

)E(X

j

)

=

E(X

i

X

j

)

−−−−

E(X

i

)E(X

j

).

Z własności 3) wynika, że dla każdej pary niezależnych

zm. l. X

i

i X

j

cov(X

i

, X

j

)

=

0. Odwrotne stwierdzenie jest fał-

szywe. Ilustruje to następujący przykład.

Przykład 7. Obliczyć kowariancję oraz zbadać niezależność
zm. l. brzegowych dla wektora l. (X, Y) o łącznym rozkładzie:

X \Y

1

2

3

6

0,2

0

0,2

8

0

0,2

0

10 0,2

0

0,2

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

34

Rozwiązanie.

Po wykonaniu obliczeń mamy: E(X)

=

8, E(Y)

=

2, E(XY)

=

16, zatem cov(X, Y)

=

0, więc zm. l. X i Y są

nie-

skorelowane

, ale nie są niezależne, gdyż

P(X

=

6, Y

=

1)

=

0,2

≠

(0,4) (0,4)

=

P(X

=

6) P(Y

=

1).

Niech na (

Ω

, B, P) określone będą zm. l. X

1

, X

2

,…, X

n

o

wartościach rzeczywistych.

Współczynnikiem korelacji

(

Correlation coefficient

) zm. l.

X

i

, X

j

(i, j

=

1, 2,…, n) nazywamy charakterystykę liczbową

ρ

ij

określoną wzorem

)

(

D

)

(

D

)

,

(

Cov

j

i

j

i

ij

X

X

X

X

=

ρ

,

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

35

Współczynnik korelacji jest wielkością nie mianowaną.

Przykład 8. Obliczyć współczynnik korelacji zachorowalno-
ś

ci na raka i nałogowego palenia papierosów S na podstawie

danych z przykładu palenie i rak.

Rozwiązanie.

Łączny i brzegowe rozkłady zostały wyzna-

czone wcześniej

C \ S 0 1

0
1

40/60 10/60
7/60 3/60

50/60
10/60

47/60 13/60

1

Tablica 1. Łączny rozkład.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

36

E(C)

=

10/60, E(S)

=

13/60, E(CS)

=

3/60, cov(C, S)

=

5/360,

E(C

2

)

=

10/60, E(S

2

)

=

13/60, D

2

(C)

=

5/36, D

2

(S)

=

611/3600.

Odchylenia standardowe D(C)

≈

0,372678, D(S)

≈

0,411974,

stąd

ρ

(C, S)

≈

0,090462.

Własności.
Dla dowolnej pary zm. l. X

i

, X

j

zachodzi własność

−

1

≤

ρ

(X, Y)

≤

1.

Ponadto dla dowolnych stałych a, b, c, d

cov(aX

+

b, cY

+

d)

=

ac cov(X, Y).

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

37

Zatem, jeśli stałe a i c są tego samego znaku, to współ-

czynnik korelacji zm. l. aX

+

b i cY

+

d jest taki sam, jak zm.

l. X i Y. Oznacza to, że współczynnik korelacji nie zależy od
przyjętej skali oraz od położenia początku układu współrzęd-
nych, w którym są rejestrowane zm. X i Y.

Własność

ρ

(X, Y)

=

1 zachodzi wtedy i tylko wtedy, gdy

Y

=

aX

+

b z prawdop. 1.

Jeśli

∀

i

=

1, 2,…, n

D

2

X

i

<

∞

, to macierz

cov(X

1

, X

2

,…, X

n

)

=

[cov(X

i

, X

j

)]

i,j

=

1,…, n

nazywamy

macierzą kowariancji

zm. l. X

1

, X

2

,…, X

n

.

Macierzą korelacyjną

(

correlation matrix

) zm. l. X

1

, X

2

,…,

X

n

nazywamy macierz corr(X

1

, X

2

,…, X

n

)

=

[

ρ

ij

)]

i,j

=

1,…, n

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

38

7. Zm. l. standaryzowana i jej własności

Standaryzacją

zm. l. X o skończonej wartości oczekiwanej

m

X

i odchyleniu standardowym

σ

X

> 0 nazywamy przekształ-

cenie Z

=

h(X) określone wzorem:

X

X

m

X

X

h

σ

−

=

)

(

Zm. l.

Z

nazywamy

standaryzowaną zm. l.

(

standardized r.

v.

)

Standaryzacja zm. l. może być uogólniona na tak zwaną

„

zm. l. zredukowaną

”, która jest określana za pomocą innej

charakterystyki położenia i/lub innej charakterystyki skali.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

39

Własności.

Niech Z będzie standaryzowaną zm. l. dla zm. l.

X, wówczas

a)

E(Z)

=

0

−

wartość oczekiwana stand. zm. l. wynosi 0,

b)

D

2

(Z)

=

1

−

wariancja stand. zm. l. wynosi 1,

c)

γ

1

(Z)

=

γ

1

(X)

−

niezmienniczość skośności na standaryza-

cję,

d)

)

/

)

((

)

(

X

X

Z

X

m

x

F

x

F

σ

−

=

−

związek między dystrybuan-

tami.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

40

8. Nierówność Czebyszewa

1

Jeżeli zm. l. X ma skończoną wartość oczekiwaną i dodat-

nią wariancję, to dla dowolnego k > 0 zachodzi oszacowanie
zwane

nierównością Czebyszewa

2

1

P

k

k

m

X

X

X

≤















≥

σ

−

lub równoważne

(

)

2

2

P

k

k

m

X

X

X

σ

≤

≥

−

.

1

Pafnucy Lwowicz Czebyszew (1821

−

1894)

−

matematyk rosyjski. Jeden z twórców petersburskiej szkoły matematycznej.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

41

Przykład 9. Niech X będzie liczbą sukcesów w 20 próbach,
gdzie prawdop. sukcesu w jednej próbie wynosi p

=

0,4.

a)

Oszacować z dołu prawdop., że liczba sukcesów będzie
zawarta między 4 i 12.

b)

Obliczyć dokładną wartość prawdop.

Rozwiązanie.

a) Ponieważ E(X)

=

20

⋅

0,4

=

8 oraz D

2

(X)

=

4,8, więc do oszacowania prawdop. korzystamy z nierówności
Czebyszewa dla k

=

4,

)

4

(

P

1

)

4

(

P

)

12

4

(

P

>

−

−

=

≤

−

=

≤

≤

m

X

m

X

X

7

,

0

16

8

,

4

1

)

4

(

P

1

=

−

≥

≥

−

−

≥

m

X

.

b) Dokładne obliczenia z rozkładu Bin(20; 0,4) to 0,96301.

K.J. Andrzejczak, MPiS30 W06: Charakterystyki liczbowe zmiennej losowej

42

9. Nierówność Gaussa

2

Jeżeli zm. l. X typu ciągłego ma skończoną wartość ocze-

kiwaną i dodatnią wariancję oraz ma rozkład jednomodalny i
symetryczny, to zachodzi lepsze oszacowanie od nierówności
Czebyszewa zwane

nierównością Gaussa

2

9

4

P

k

k

m

X

X

X

≤













≥

σ

−

2

Carl Friedrich Gauss (1777-1855)

−

matematyk niemiecki. Jeden z najwybitniejszych matematyków wszyst-

kich czasów, zwany przez współczesnych książę matematyków. Profesor uniwersytetu w Getyndze.