Damian Mieczysław Domalewski (nr indeksu 172244)	Grupa: Marcin Motyka
Wyznaczanie promieni krzywizny soczewki i długości fali świetlnej za pomocą pierścieni Newtona	16.03.2009r.

1. Cel ćwiczenia:

Celem ćwiczenia było zapoznanie się ze zjawiskiem interferencji światła występującym w klinie optycznym oraz zastosowanie tego zjawiska do celów

pomiarowych.

2. Wstęp:

Na laboratoriach z fizyki badaliśmy soczewki, a ściślej mówiąc ich krzywiznę, czyli promień. Do wykonania tego doświadczenia korzystaliśmy z mikroskopu, lampy z filtrem interferencyjnym, płytki płaskorównikowej oraz przedmiotowej, badanej, soczewki.

Po odpowiednim ustawieniu całości przyrządów pomiarowych, można było dojrzeć w okularze mikroskopu charakterystyczne pierścienie, zwane pierścieniami Newtona. Badanie krzywizny soczewki polegało na tym, że mierzyło się poszczególne prążki

(a raczej ich skrajne położenie), spisując za kaczym razem położenie wskazań zegara, co pozwoliło mi na wyznaczenie średnic badanych prążków. Czynność tę powtarzałem sześć razy. Zebrane dane zostały umieszczone w tabeli 1. Do dalszych obliczeń korzystałem ze wzorów na: promień krążka (2.01), średnią arytmetyczną (2.02), obliczenie promienia krzywizny soczewki (2.03), obliczenie długości fali (2.04), obliczenie granicy błędu promienia krążków (2.05), obliczenie granicy błędu promienia krzywizny soczewki (2.06),

obliczenie granicy błędu długości fali (2.07).

W części obliczenia pokazałem sposób, w jaki korzystałem ze wzorów, na pojedynczych przykładach. Reszta obliczeń została zrobiona adekwatnie do pokazanych

przykładów.

Interferencja (łac. inter - między + ferre - nieść) to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej. Interferencja zachodzi dla wszystkich rodzajów fal, we wszystkich ośrodkach, w których mogą rozchodzić się dane fale. W ośrodkach nieliniowych oprócz interferencji zachodzą też inne zjawiska wywołane nakładaniem się fal, w ośrodkach liniowych fale ulegając interferencji spełniają

zasadę superpozycji.

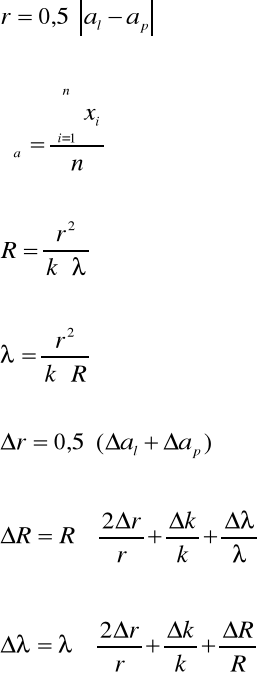
2.01.

2.02.

2.03.

2.04.

2.05.

2.06.

2.07.

3. Zebrane dane:

Lp.		K	al.	ap	al	ap
	[nm]		[mm]	[mm]	[mm]	[mm]
1			65,42	1,15
2			67,00	7,85
3	540	4	67,42	5,50	0,01	0,01
4			68,48	5,85
5			64,48	2,94
6			62,48	4,00
1			35,68	72,05
2			26,09	70,45
3	540	2	25,09	70,65	0,01	0,01
4			26,99	69,15
5			26,15	70,95
6			26,10	73,05

Tabela 1. zestawienie zebranych danych.

4. Obliczenia:

• Sposób wyliczenia długości promienia krążków (wzory: 2.01; 2.02):

• Sposób wyliczenia błędu promienia krążków (wzór: 2.05):

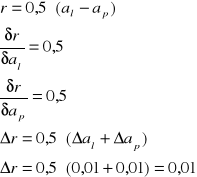
• Sposób wyliczenia promienia krzywizny soczewki (wzór: 2.03):

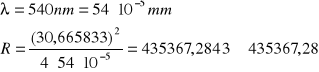
• Sposób wyliczenia błędu pomiaru krzywizny soczewki (wzór: 2.06):

5. Zestawienie danych zebranych i obliczonych:

Lp.		K	al.	Śr. al.	al	ap	Śr. ap	ap
	[nm]		[mm]	[mm]	[mm]	[mm]	[mm]	[mm]
1			65,42			1,15
2			67,00			7,85
3	540	4	67,42	65,88	0,01	5,50	4,55	0,01
4			68,48			5,85
5			64,48			2,94
6			62,48			4,00
1			35,68			72,05
2			26,09			70,45
3	540	2	25,09	27,68	0,01	70,65	71,05	0,01
4			26,99			69,15
5			26,15			70,95
6			26,10			73,05

	r	r	R	R	R/R
	[mm]	[mm]	[mm]	[mm]	
	30,67	0,01	435367,28	1090,18	0,0025
	21,68	0,01	435339,76	8463,39	0,0194
		Wynik uśredniony	435353,52	4776,78	0,0110

Tabela 2. Zestawienie wartości zmierzonych i obliczonych (wartości zaokrąglone).

6. Zebrane dane:

Lp.	K	al.	ap	al	ap	R	R
		[mm]	[mm]	[mm]	[mm]	[mm]	[mm]
1		45,57	13,05
2		43,00	16,25
3	2	36,05	13,95	0,01	0,01	435353,52	4776,78
4		44,18	13,15
5		43,05	16,34
6		45,16	13,35
1		98,18	35,04
2		64,62	36,99
3	3	99,99	32,50	0,01	0,01	435353,52	4776,78
4		98,10	34,15
5		81,32	33,10
6		99,08	32,01

Tabela 3. Zestawienie zebranych danych do wyznaczenia długości fali świetlnej

(wartości zaokrąglone).

7. Obliczenia:

• Sposób wyliczenia długości promienia krążków (wzory: 2.01; 2.02):

• Sposób wyliczenia błędu pomiaru krążków (wzór: 2.05):

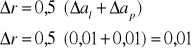
• Sposób wyliczenia długości fali świetlnej (wzór: 2.04):

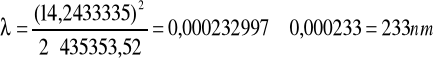
• Sposób wyliczenia błędu pomiaru długości fali świetlnej (wzór: 2.07):

8. Zestawienie danych zebranych i obliczonych:

Lp.	K	al.	Śr. al.	al	ap	Śr. ap	ap	r	r
		[mm]	[mm]	[mm]	[mm]	[mm]	[mm]	[mm]	[mm]
1		45,57			13,05
2		43			16,25
3	2	36,05	42,84	0,01	13,95	14,35	0,01	14,24	0,01
4		44,18			13,15
5		43,05			16,34
6		45,16			13,35
1		98,18			35,04
2		64,62			36,99
3	3	99,99	90,22	0,01	32,5	33,97	0,01	28,13	0,01
4		98,1			34,15
5		81,32			33,1
6		99,08			32,01

	R	R			
	[mm]	[mm]	[mm]	[mm]	100%
	435353,52	244219,62	0,000233	2,88* 10^-6	0,0124
	435353,52	244219,62	0,000606	7,08*10^-6	0,0117
		Wartość uśredniona	0,000419	4,98*10^-6	0,0120

Tabela 4. Zestawienie wartości zmierzonych i obliczonych (wartości zaokrąglone).

9. Prezentacja wyników:

Kolor filtra	Średnica krzywizny soczewki	Długość fali świetlnej
Zielone	435,35 m 4,78 m	540 nm
Fioletowo- niebieskie	435,35 m 4,78 m	419 nm 2 nm

Analizując powyższe widmo z zaznaczonymi wartościami nanometrów można zauważyć, iż długość fali światła wyszła prawidłowa.

10. Wnioski:

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

2

---