Ćwiczenie 9 - 32 -

Przykład 30

Punktowi materialnemu o masie m, leżącemu na równi pochyłej nachylonej pod kątem α = 43⁰ do poziomu, nadano pewną prędkość początkową skierowaną w górę równi wzdłuż linii jej największego spadku. Należy wyznaczyć opóźnienie, z którym punkt ten porusza się w górę równi. Współczynnik tarcia kinetycznego równy jest μ = 0.45.

Rozwiązanie

x

N y

V x

y G sinα 0

0 α

T G G cosα

G

α Rys. 30

Równania ruchu :
(a)

y = 0,
,
dlatego
, stąd

ponieważ
to

Równanie (a) przyjmuje postać:

Przykład 31

Dwa ciała materialne o masach m₁ = 1.2 kg i m₂ = 1.7 kg, leżące na poziomej chropowatej płaszczyźnie, połączone zostały nierozciągliwym cięgnem BA, tak

jak pokazano na rysunku 31. Obliczyć wartość przyśpieszenia tych ciał oraz napięcie cięgna BA wywołane działaniem poziomej siły P przyłożonej do ciała o masie m₁. Współczynnik tarcia kinetycznego między ciałem m₁ a poziomą płaszczyzną ma wartość μ₁ = 0.32, natomiast między ciałem m₂ a płaszczyzną ma wartość μ₂ = 0.26. Masę cięgna należy pominąć, P = 10 N.

m₂ B A m₁ P

Rys. 31

- 33 -

N₂ N₁ y

m₂ S₂ - S₂ B A -S₁ S₁ m₁ P x

T₂

T₁ Rys. 31a

G₂ G₁

G₂ = m₂ g, T₂ = μ₂ N₂ ; G₁ = m₁ g, T₁ = μ₁ N₁

Siły działające na masę 1

,
,
,

Z równowagi pręta BA którego masy nie uwzględniamy

(b)

Siły działające na masę 2

,
,
,

(c)

Ponieważ pręt BA porusza się ruchem postępowym to
,

stąd
(d)

Z równania (b)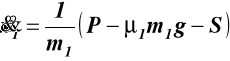

Z równania (c)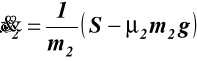
(e)

Z warunku (d)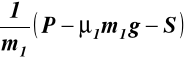

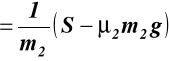
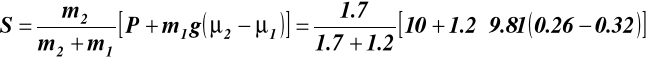
Z równania (e)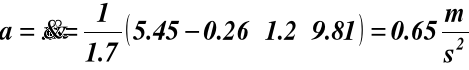

Przykład 32 - 34 -

Pod jakim kątem należy wystrzelić pocisk o masie m, aby osiągnąć maksymalny zasięg strzału L, przy znanej prędkości początkowej pocisku V₀. Określić również wartości maksymalnego zasięgu L, oraz maksymalną wartość wysokości h jaką osiągnie pocisk. Opór powietrza pominąć. Dane V₀ = 350 m/s, g = 9.81 m/s².

Rozwiązanie

y m

V₀

G y h G = mg

α

0 x

x

L Rys. 32

Równania różniczkowe ruchu:
,
(a)

Całkujemy równania różniczkowe ruchu (a) otrzymujemy kolejno

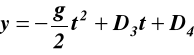
(b)

Warunki początkowe. Dla t = 0

(c)

Podstawiając (c) do (b) otrzymujemy:

,
,
,
(d)

Podstawiając (c) do (b) otrzymujemy:

,

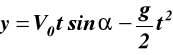
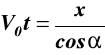
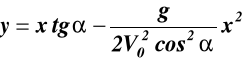
(e)

równanie (e) opisuje parabolę (rys.32).

Z rys. 32 wynika, że L określamy z warunku, że dla y = 0, x_max = L

podstawiając do (e) y = 0 otrzymujemy:

,
,

,
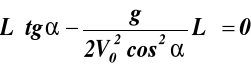
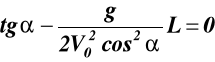
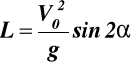
występuje dla
,

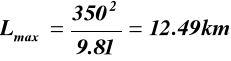
Wartość h określamy z warunku: - 35 -

, dla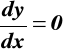
patrz rys.32, różniczkujemy (e)

,

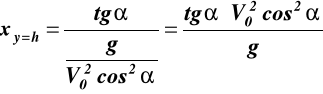
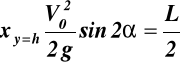
po podstawieniu
do (e)

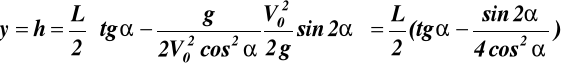
dla α = 45⁰

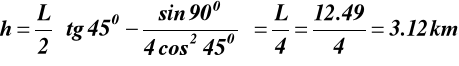
Przykład 33

Samolot lecący na wysokości h = 4500 m z poziomą prędkością V₀ = 930 km/h

zrzuca bombę na cel A znajdujący się na ziemi. Należy wyznaczyć, w jakiej odległości L od celu (rys. ) pilot musi wyrzucić bombę. Dane g = 9.81 m/s², przy obliczeniach pominąć opór powietrza.

z

m

mg

h z

x

x Rys.

L

Rozwiązanie

Równania różniczkowe ruchu toru bomby o masie m

,

Ponieważ P_x = 0, P_z = - mg to

,
(a)

Całkując równania (a) otrzymujemy:

- 36 -

,

,
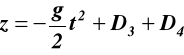
(b)

Warunki początkowe ruchu

,
,
,
(c)

Wstawiając (c) do (b) otrzymujemy stałe całkowania:

D₁ = V₀, D₂ = 0, D₃ = 0, D₄ = h (d)

Wstawiając stałe całkowania (d) do (b) otrzymujemy równania ruchu

,

Po wyrugowaniu z tych równań czasu t otrzymujemy równanie toru bomby

,

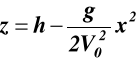
jeśli z = 0 to x = L stąd

,
,
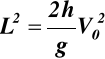
stąd

V₀

A

0

---