Ćwiczenia 14 - 55 -

Twierdzenie Koeniga
(a)

Przykład 53

Jednorodny krążek kołowy o masie m = 22 kg i promieniu r = 0.35 m obraca się wokół swej osi geometrycznej ze stałą prędkością kątową, wykonując n = 10 obr/s. Wyznaczyć energią kinetyczną krążka.

r

C ω

Rys. 53

Rozwiązanie

Dla V_C = 0 wzór (a) ma postać
gdzie l jest osią obrotu krążka

a I_l momentem bezwładności krążka względem osi l

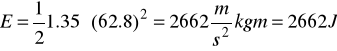
Odpowiedz: Energia krążka wynosi 2662 dżuli

Przykład 54

Jednorodny krążek o promieniu r = 20 cm i masie m = 2 kg toczy się bez poślizgu po poziomej prostej, przy czym prędkość jego środka C równa jest V_C = 20 cm/s (rys.54).

Wyznaczyć wartość energii kinetycznej krążka.

C V_C ω

Rys. 54

A

Rozwiązanie

stąd

Przykład 55 - 56 -

Na bęben, który może obracać się bez tarcia wokół poziomej osi, nawinięto wiotką i nierozciągliwą linę, na której końcu zawieszono ciało o masie m = 8 kg (rys.55). Należy obliczyć prędkość tego ciała, gdy opuści się ono z wysokości równej h = 0.3m. Promień bębna r = 5 cm, masa bębna M = 2 kg. Masę liny pominąć.

r

C ω

Rys. 55

V = 0

mg h

V = ωr

Rozwiązanie

gdzie
jest przyrostem energii układu, W jest pracą sił zewnętrznych

;
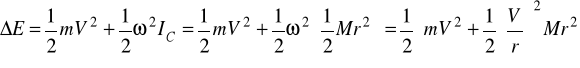
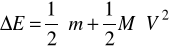
stąd

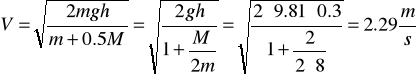
Przykład 56

Cienki jednorodny pręt OA o długości l i masie m może obracać się bez tarcia wokół poziomej osi prostopadłej do osi pręta i przechodzącej przez jego koniec O. Pręt wychylono z położenia równowagi i ustawiono w ten sposób, że jego oś zajmowała położenie poziome i następnie oswobodzono. Obliczyć jaką będzie miał prędkość koniec A pręta w chwili gdy oś pręta będzie tworzyła z poziomem kąt α (rys.56).

Rozwiązanie

A

0 C V = 0 h =0.5 lsinα

h W = mgh =0.5 mglsinα

α 0A = l

mg 0C = CA = 0.5l

V Rys.56

;
;

---