[2] Zasada d'Alemberta
Rozważmy układ materialny nieswobodny (poddany więzom) złożony z n punktów materialnych opisany następującymi równaniami ruchu
![]()
i=1,…,n, (2.1)
przy czym Fi, Wi i Ri oznaczają odpowiednio siły zewnętrzne, wewnętrzne i reakcje.
Niech każdy z punktów materialnych dozna przesunięcia przygotowanego δri, gdzie ri jest promieniem wodzącym punktu i. Mnożąc obydwie strony równania (2.1) przez
δri i dodając stronami otrzymujemy:
![]()
(2.2)
Zakładając, że rozważamy jedynie więzy idealne, które z definicji spełniają zależność
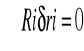
(2.3)
to równanie (2.1) przyjmie postać
![]()
(2.4)
Otrzymane równanie pozwala na sformułowanie zasady d'Alemberta. Brzmi ona następująco:
Suma iloczynów skalarnych przesunięć przygotowanych oraz sił zewnętrznych, wewnętrznych i wektorów (-miai) punktów układu materialnego jest równa zeru.
Dokonując rzutowania wektorów występujących w równaniu (2.4) na osie przyjętego prostokątnego układu współrzędnych (xyz) otrzymujemy
![]()
(2.5)
Otrzymane równanie często nazywane jest równaniem ogólnym mechaniki. Warto podkreślić, że zostało ono otrzymane z wcześniej wprowadzonych praw Newtona. Ponieważ rozważamy układ swobodny, to wszystkie przesunięcia przygotowane są niezależne. Oznacza to, że równanie ogólne będzie spełnione wówczas, gdy wyrażenia w nawiasach będą równe zeru.
Otrzymujemy wówczas 3n równań różniczkowych rzędu drugiego o postaci
![]()
,
![]()
, (2.6)
![]()
.
Powyższe równania upraszczają się jeszcze bardziej, gdy suma sił wewnętrznych jest równa zeru, przyjmując postać:
![]()
,
![]()
, (2.7)
![]()
.
Powyższe trzy równania mogą być zapisane w następującej postaci wektorowej
![]()
(2.8)
Powyżej przyjęto, że siła ![]()
. Zwana jest ona siłą bezwładności lub siłą d'Alemberta działającą na punkt materialny i. Posiada ona zwrot przeciwny do siły czynnej Fi.
Wyszukiwarka
Podobne podstrony:
S, Zasada d'Alemberta
S Zasada d Alemberta
SPRAW2TS, Celem ˙wiczenia jest praktyczne zapoznanie si˙ z zasadami fotometrii oraz prostymi metodam
skaner zasada dzialania1
Wykład Ch F I zasada
F 1 Zasada działania tranzystora bipolarnego
08 Zasada zachowania energii
Budowa pojazdów samochodowych -Zasada działania silnika dwusuwowego semestr 1, Motoryzacja
Zasada subsydiarności w Unii Europejskiej, instytucje i źródła prawa UE
Zasada PARETO
Weiderowska Zasada Treningu Cyklicznego, Sport
kanon medycyny chińskiej zasada 5 elementów cykl karmiący cz V
,Analiza chemicznych zanieczyszczeń środowiska , Zasada powstawania widma mas
,pytania na obronę inż,Zasada projektowania cyklonów
Budowa i zasada działania układu pneumatycznego z?S oraz kryteria oceny
I zasada Termodynamiki
więcej podobnych podstron