1. Wstęp teoretyczny :

Jeżeli w jednorodnym polu magnetycznym wstrzelimy prostopadle do linii sił tego pola elektron

(o ładunku = -e) z prędkością ν ,to na ten ładunek działa siła:

gdzie:

-wektory pola elektrycznego i indukcji magnetycznej;

q- ładunek próbny;

-wektor prędkości ładunku;

Wynikiem działania siły na elektron będzie zakrzywienie jego toru w płaszczyźnie prostopadłej do kierunku wektora
.Ponieważ elektron wciąż porusza się w kierunkach prostopadłych do
,to kąt α stale wynosi π/2 i wartość bezwzględna siły Lorentza jest stała ,a więc torem elektronu jest okrąg . Zjawisko to zwie się efektem magnetronowym . Posłuży ono do wyznaczenia wartości e/m.

Aby tego dokonać należy określić równocześnie trzy wielkości fizyczne :wielkość indukcji magnetycznej , prędkość wstrzelenia elektronu w pole oraz promień okręgu ,po którym on krąży w polu magnetycznym. Trudno jest wyznaczyć przy ustalonym polu magnetycznym krzywiznę toru elektronu ,więc w ćwiczeniu odbędzie się postępowanie odwrotne - poszukamy pola o takiej indukcji B , aby elektron krążył z góry wyznaczonym torze (określ. r).

Do tego służy dioda lampowa ,w której cienki drut (katoda) umieszczony jest w osi cylindrycznej anody .Elektrony wychodzące z tejże katody biegną promieniście do anody uzyskując przy tym prędkość

gdzie Ua jest napięciem przyłożonym między katodę i anodę .

W diodzie lampowej o promieniach anody i katody (odpowiednio ra i rk ;ra <rk)

tor elektrony zostanie tak zakrzywiony ,aby był on styczny do powierzchni anody ,czyli promień musi wynosić:

Wartość indukcji w której sytuacja ta nastąpi nazwiemy krytyczną i oznaczymy Bkr.

Dioda lampowa umieszczona jest w polu magnetycznym wytwarzanym przez cewkę z prądem . Znając natężenie w polu magnetycznym prądu I płynącego w solenoidzie można wyznaczyć indukcję magnetyczną pola w pobliżu środka cewki za pomocą wzoru :

B = β I

gdzieβ oznacza empirycznie wyznaczoną stałą .

Celem ćwiczenia jest znalezienie wartości krytycznej indukcji pola magnetycznego, przy której wystąpi sytuacja zakrzywienia toru elektronu w taki sposób, aby był on styczny do powierzchni anody. Należy też wyznaczyć stosunek e do m , oraz zbadać zależność prądu anodowego I_A funkcji indukcji B przy ustalonym napięciu anodowym.

2. Wyniki pomiarów i obliczeń :

1. Tabela z wynikami pomiaru :

I [mA]	Ua = 5V	Ua = 8V	Ua =11V
		Ia [μA]	Ia [μA]	Ia [μA]
0	160	300	460
20	160	300	460
40	160	300	450
60	160	300	445
80	150	300	445
100	150	295	445
110	145	295	445
120	140	290	445
130	120	280	440
140	110	260	420
150	90	240	405
160	85	195	340
170	65	165	300
180	60	150	250
190	55	135	235
200	50	120	210
220	45	110	190
240	45	100	170
260	45	90	155
280	45	85	140
300	40	80	135
320	40	80	130
340	40	75	130
360	40	75	115

b) Wyznaczenie wartości prądu I_kr z wykresu I_a = f(I) :

• dla U_a1 = 5V

I_kr1 = 151 [mA]

• dla U_a2 = 8V

I_kr2 = 161 [mA]

• dla U_a3 = 11V

I_kr3 = 174 [mA]

3. Wyznaczenie B_kr dla wybranej wartości U_a :

- dla U_a = 8V

4. Wyznaczenie ładunku właściwego elektronu :

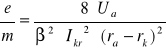
• dla U_a1 = 5V

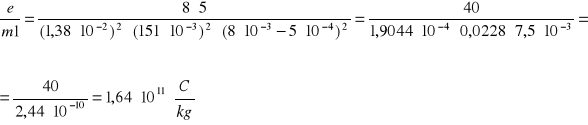
-dla U_a1 = 8V

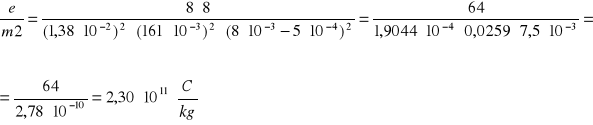
-dla U_a1 = 11V

5. Obliczam średnią arytmetyczną wartość ładunku właściwego elektronu :

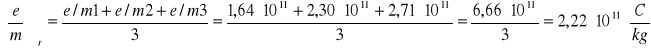
6. Obliczam błąd graniczny bezwzględny i względny wartości ładunku właściwego elektronu :

• wyznaczam pochodne cząstkowe po kolejnych zmiennych :

δ U_a = 8 β^-2 I_{kr śr} ^-2 (r_a - r_k)^-2 ΔU_a

δβ = - 16 β^-3 I_{kr śr} ^-2 (r_a - r_k)^-2 Δ β U_{a śr}

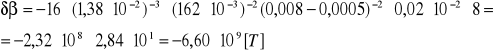
δI_kr = - 16 β^-2 I_{kr śr} ^-3 (r_a - r_k)^-2 ΔI_kr U_{a śr}

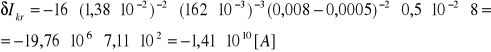
δr = - 16 β^-2 I_{kr śr} ^-2 (r_a - r_k)^-3 Δr U_{a śr}

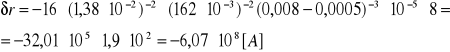
• wyznaczam błąd graniczny bezwzględny pomiaru e/m :

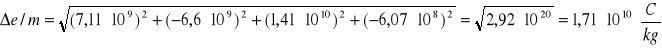
• wyznaczam błąd graniczny względny pomiaru e/m :

δ e/m = Δ e/m * e/m_e^-1

3. Wnioski i ocena otrzymanych wyników :

Podczas ćwiczeń otrzymaliśmy następującą wartość pomiaru ładunku właściwego elektronu :

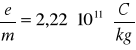
Na podstawie otrzymanych wyników i po porównaniu ich z wartością tablicową ładunku właściwego elektronu (
[C/kg]) możemy stwierdzić, że wynik wyznaczono z dużą dokładnością (ok. 10%). Po analizie rachunku błędu przeprowadzonego w punkcie 2.f sprawozdania widzimy, że największy wpływ na wielkość błędu miały pomiary napięcia anodowego i prądu krytycznego (odczytanego z wykresu).

---