Katedra Fotogrametrii i Teledetekcji
3.Fotogrametryczna ocena zdjęć lotniczych
4.Analityczna analiza pojedynczego zdjęcia lotniczego
Wykonawcy:
Katarzyna Detyna
Aneta Norowska
Marcin Siepsiak
GiSzN Rok III Grupa II
FOTOGRAMETRYCZNA OCENA ZDJĘĆ LOTNICZYCH
W zależności od położenia osi optycznej kamery lotniczej, w momencie ekspozycji, w stosunku do linii pionu przechodzącej przez przedni punkt główny obiektu zdjęcia lotnicze dzielimy na:
-zdjęcia poziome (kąt mniejszy niż 3o )
-zdjęcia ukośne (nachylone i perspektywiczne)
Lotnicze zdjęcia pomiarowe wykonywane są z przystosowanych samolotów typu transportowego lub ze specjalnych samolotów fotogrametrycznych. Samolot powinien odpowiadać pewnym warunkom:
-duży zasięg lotu
-pułap
-prędkość lotu dla wykonania zdjęć nie powinna być zbyt duża, prędkość lotu oraz czas ekspozycji muszą być ze sobą zsynchronizowane
-stateczność samolotu
Wybór odpowiednich warunków technicznych dla wykonania zdjęcia lotniczego powinien uwzględniać:
charakter terenu
technologię opracowania mapy
skalę opracowanej mapy
skalę zdjęć lotniczych tym samym przekładnię skalową K
wysokość fotografowania W
typ kamery lotniczej, stałą kamery oraz format zdjęć
prędkość samolotu oraz maksymalny dozwolony czas naświetlania
pokrycie podłużne oraz poprzeczne zdjęć
rodzaj materiału światłoczułego , warunki fotografowania
Skala zdjęć lotniczych w interpretacji geometrycznej zależy od wysokości fotografowania W, oraz stałej kamery CK. Stąd też skalę zdjęcia można obliczyć ze wzoru
Mz = CK / W
Skala zdjęć jest uzależniona od wielkości CK. Wybór stałej kamery CK uzależniony jest także od sposobu wykorzystania zdjęć i deniwelacji terenu. Ogólnie przyjmuje się że do opracowywania fotomap korzystamy z CK jak najdłuższego, a do opracowań autogrametrycznych jak najkrótszych. W pierwszym przypadku, długa CK oraz duża wysokość fotografowania W powodują mniejsze zniekształcenie obrazu terenu na zdjęciu, ze względu na deniwelację. W drugim przypadku , krótka CK oraz mała wysokość lotu powodują przesunięcia perspektywiczne pionowych form terenu odfotografowanych na zdjęciach.
Lotnicze zdjęcia pomiarowe wykonywane są szeregowo. Pokrycie wzajemne dwóch sąsiednich zdjęć w szeregu wynosi około 60 - 80 % ich powierzchni, odstępy między osiami szeregów zdjęć standardowo wynosi około 20 - 40% powierzchni tych zdjęć. Pokrycie podłużne i poprzeczne zdjęć lotniczych na danym obszarze ma za zadanie wyeliminowanie występowania przerw fotogrametrycznych. Przy wyborze pokrycia podłużnego i poprzecznego należy też uwzględnić charakter terenu.
Do ćwiczenia wykorzystano dwa szeregi: 9 i 10. W szeregu 9: zdjęcia o nr 617-636, a w 10: 642-654. Analizowane zdjęcia w szeregu 9 miały mianownik skali zdjęcia Mz=5620, a w szeregu 10 : Mz=5600
W celu obliczenia pokrycia podłużnego (p%)
9 szeregu wzięto pod uwagę 3 pary zdjęć o numerach: 617 i 618, 626 i 627, 635 i 636.
p1%=(13,7/22,6)*100%=60,6%
p2%=(15,0/22,6)*100%=66,4%
p3%=(12,0/22,6)*100%=53,1%
pśr%=60%
10 szeregu wzięto pod uwagę 3 pary zdjęć o numerach: 642 i 643, 648 i 649,653 i654.
p1%=(15,2/22,6)*100%=67,2%
p2%=(13,8/22,6)*100%=61,1%
p3%=(14,8/22,6)*100%=65,5%
pśr%=65%
W celu obliczenia pokrycia poprzecznego (q%) szeregów 9 i 10 wzięto pod uwagę trzy pary zdjęć o numerach: 634 i 654, 628 i 648, 622 i 642
q1%=(9,3/22,6)*100%=41,2%
q2%=(9,7/22,6)*100%=42,9%
q3%=(8,3/22,6)*100%=36,7%
qśr%=40%
Kąt znosu szeregu
9
tgα=4,5/40 → α=7,1320g
10
tgα= 0,5/30 → α=1,0609g
Powierzchnia użyteczna pojedynczego fotogramu
Pz = (Lx'y' Mz )2
Pz = (22,6 x 5620 )2
Pz ≈ 161ha
Pojemnośc informacyjna zdjęć lotniczych jest uwarunkowana ich zdolnością rozdzielczą. Zdolność rozdzielcza jest limitowana przez kilka czynników:
zdolność rozdzielczą obiektywu Ro
zdolność rozdzielczą filmu RF
rozmazanie obrazu spowodowane ruchem postępowym samolotu RFM
rozmazanie obrazu spowodowane ruchami kątowymi kamery RAM
kontrast obiektu
wpływ atmosfery
zdolność rozdzielczą filmu duplikacyjnego ( w przypadku duplikowania) RD
Znając wartości poszczególnych składowych procesu fotografowania wyrażone w parach linii/mm można określić wynikowa zdolność rozdzielczą zdjęć RZDJ:
1/(RZDJ)2 = 1/(RO)2 +1/(RF)2 + 1/(RFM)2 + 1/(RAM)2 +1/(RD)2
Współczesne zdjęcia lotnicze chrakteryzują się rozdzielczością:
- ok. 55 par linii/mm dla obiektów kontrastowych (1 pl/mm = 18 μm)
- ok. 40 par linii/mm dla obiektów o niskim kontraście (1 pl/mm = 25 μm)
ANALIZA POJEDYNCZEGO ZDJĘCIA LOTNICZEGO
Elementy orientacji zdjęcia lotniczego dzielimy na:
elementy orientacji wewnętrznej,elementy orientacji zewnętrznej
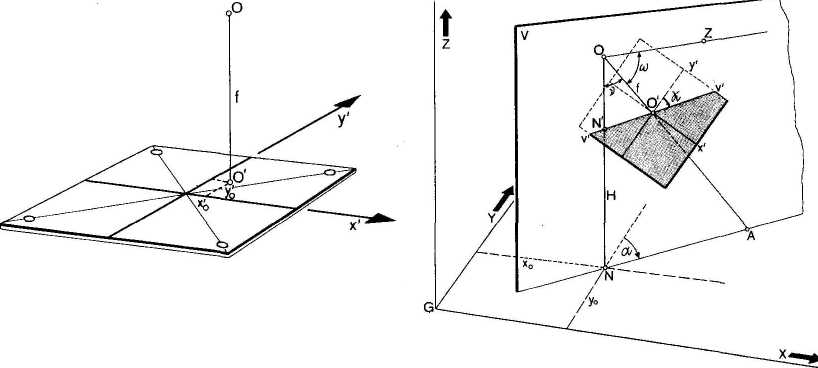
Elementami orientacji wewnętrznej zdjęcia lotniczego nazywamy wielkości umożliwiające określenie położenia środka rzutów O w stosunku do płaszczyzny zdjęcia.
Elementami orientacji wewnętrznej są zatem:
współrzędne tłowe głównego punktu zdjęcia O' (x'o, y'o);
ogniskowa kamery f, tj. odległość między głównym punktem obrazowym obiektywu kamery a płaszczyzną obrazu (płaszczyzną ramki tłowej). Jest ona odpowiednikiem odległości środka rzutu O od rzutni n.
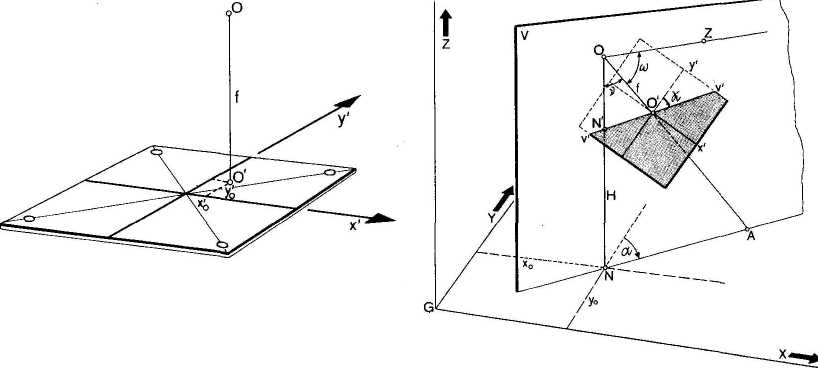
Elementy orientacji zewnętrznej zdjęcia lotniczego są to wielkości określające położenie kamery względem fotografowanego terenu. Umożliwiają one wyznaczenie orientacji przestrzennej wiązki promieni rzutujących w momencie wykonywania zdjęcia.
Elementami tymi są:
współrzędne przestrzenne środka rzutów Xo Yo Zo (w układzie współrzędnych prostokątnych, przyjętym do prac po miarowych w terenie);kąt nachylenia zdjęcia v - kąt nachylenia płaszczyzny zdjęcia w stosunku do płaszczyzny poziomej. Może być on również określony jako kąt odchylenia osi kamery od pionu, a więc kąt zawarty między prostą pionową przechodzącą przez środek optyczny obiektywu a osią optyczną kamery fotograficznej. Kąt v rozkłada się na dwa kąty składowe: wzdłuż osi x - kąt nachylenia podłużnego φ i wzdłuż osi y - kąt nachylenia poprzecznego ω;
kąt kierunkowy osi kamery (azymut zdjęcia) α. Jest to kąt zawarty między kierunkiem początkowym terenowego układu współrzędnych (dodatnim kierunkiem osi Y) a rzutem prostokątnym osi optycznej kamery na płaszczyznę XY;
kąt skręcenia zdjęcia χ . Jest to kąt zawarty między prostą największego spadku v'v' a dodatnim kierunkiem osi y', mierzony w płaszczyźnie zdjęcia, w kierunku zgodnym z ruchem wskazówki zegara.
Elementy ramki zdjęcia lotniczego

Legenda:
1 i 8 - znaczki tłowe
2 - libella (kąt nachylenia kamery równy 2o)
3 - zegar
4 - wysokościomierz ( wysokość lotu 180m)
5 - numer kamery lotniczej
6 -numer porządkowy negatywu
7 - ogniskowa kamery (f)
Wpływ deniwelacji terenu na odwzorowanie punktu na zdjęciu
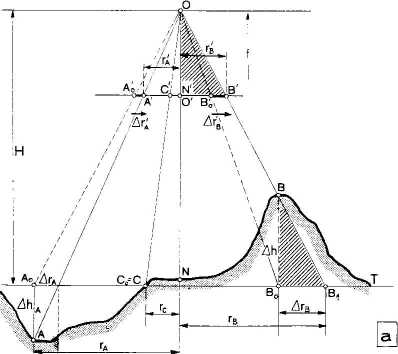
Deniwelacje terenu powodują radialne (w stosunku do punktu nadirowego N) przesunięcie obrazów punktów położonych powyżej lub poniżej płaszczyzny odpowiadającej średniej wysokości terenu T (rysunek). W rezultacie punkty terenu A i B, których rzut ortogonalny na płaszczyznę T oznaczono odpowiednio Ao i Bo odfotografowują się na zdjęciu jako punkty A' i B'. Położenie tych punktów należy więc skorygować o wartość Δr', doprowadzając do położenia A'0 i B'0. W przypadku punktu A, który leży poniżej płaszczyzny T, korekta będzie polegała na przesunięciu jego położenia o wielkość r'A w kierunku od punktu nadirowego, natomiast w przypadku punktu B, leżącego powyżej płaszczyzny T, na przesunięciu położenia o odcinek r'B skierowany do punktu nadirowego.
Wpływ deniwelacji terenu na położenie obrazu punktu jest tym większy, im bardziej jest on oddalony od punktu nadirowego, im większe jest przewyższenie tego punktu w stosunku do średniej wysokości terenu oraz im mniejsza jest wysokość fotografowania. Minimalne zniekształcenia występują w przypadku terenów równinnych i w środkowej części użytecznego pola zdjęcia.
Należy zaznaczyć, że praktycznie, w przypadku zdjęć prawie pionowych, poprawkę r'B odkładamy na promieniu Δr'B wykreślonym z głównego punktu zdjęcia O', gdyż prawie pokrywa się on z punktem nadirowym N'. Wpływ tej nieścisłości na ostateczne położenie punktu jest znikomy i nie przekracza granic dokładności graficznej
Punkty i linie szczególne zdjęcia
Punkty:
główny O'
izocentryczny I'
nadirowy N'
zbiegu Z'
Linie:
największego spadku v'v' (główna pionowa)
główna pozioma hoho
linia niezniekształconej skali hihi
linia zbiegu zz
Analizę pojedynczego zdjęcia lotniczego wykonano na diapozytywie. Zdjęcie ,o numerze 647, wykonano na wysokości 850m , aparatem o stałej kamery ck=152,07, odchylenie ν osi optycznej od linii pionu wynosi 2,5o.
Ze względu na łatwość ustalenia położenia na zdjęciu pomiarowym punktu głównego O (punkt główny na zdjęciu pomiarowym znajduje się na przecięciu linii łączących przeciwne znaczki tłowe ) , w stosunku do tego punktu określone jest położenie pozostałych punktów szczególnych:
O'N'= tgν*CK
O'Z'= ctgν*CK
O'I'= tg(ν/2)*CK
gdzie: ck - stała kamery
ν- odchylenie osi optycznej od linii pionu
ON= 6,64 mm
OZ= 3482,98 mm
OI= 3,32 mm
Cechą wspólną dla wszystkich szczególnych punktów zdjęcia pomiarowego jest to, że leżą one na jednej prostej - linii największego spadku .
dr'ν=(r'2/ck)*sinν*sinγ
dr'ν-wartość przesunięcia punktu na zdjęciu spowodowana występowaniem kąta nachylenia ν
r'- promień radialny, odległość od początku układu współrzędnych do danego punktu P na zdjęciu
γ- kąt odłożony od linii największego spadku
Wpływ nachylenia zdjęcia na położenie punktów na zdjęciu:
ck = 152,07
r'= 10 mm
v = 2o52'
γ = 0o → dr'v = 0,00
r'= 10 mm
v = 7o52'
γ = 0o → dr'v = 0,00
r'= 110 mm
v = 2o52'
γ = 0o → dr'v = 0,00
r'= 110 mm
v = 7o52'
γ = 0o → dr'v = 0,00
r'= 10 mm
v = 2o52'
γ = 45o → dr'v = 0,02
r'= 10 mm
v = 7o52'
γ = 45o → dr'v = 0,06
r'= 110 mm
v = 2o52'
γ = 45o → dr'v = 2,81
r'= 110 mm
v = 7o52'
γ = 45o → dr'v = 7,70
r'= 10 mm
v = 2o52'
γ = 90o → dr'v = 0,03
r'= 10 mm
v = 7o52'
γ = 90o → dr'v = 0,09
r'= 110 mm
v = 2o52'
γ = 90o → dr'v = 3,98
r'= 110 mm
v = 7o52'
γ = 90o → dr'v = 10,89
ck = 305,00
r'= 10 mm
v = 2o52'
γ = 0o → dr'v = 0,00
r'= 10 mm
v = 7o52'
γ = 0o → dr'v = 0,00
r'= 110 mm
v = 2o52'
γ = 0o → dr'v = 0,00
r'= 110 mm
v = 7o52'
γ = 0o → dr'v = 0,00
r'= 10 mm
v = 2o52'
γ = 45o → dr'v = 0,01
r'= 10 mm
v = 7o52'
γ = 45o → dr'v = 0,03
r'= 110 mm
v = 2o52'
γ = 45o → dr'v = 1,40
r'= 110 mm
v = 7o52'
γ = 45o → dr'v = 3,84
r'= 10 mm
v = 2o52'
γ = 90o → dr'v = 0,02
r'= 10 mm
v = 7o52'
γ = 90o → dr'v = 0,04
r'= 110 mm
v = 2o52'
γ = 90o → dr'v = 1,98
r'= 110 mm
v = 7o52'
γ = 90o → dr'v = 5,43
dr'ν rośnie wraz ze wzrostem promienia radialnego r' i kątem γ
Wpływ deniwelacji terenu na skalę zdjęcia:
dr'Δh = (r΄ * Δh) / W
gdzie
Δh - deniwelacja terenu
W - wysokość fotografowania
W = 850 m
Δh [m] r' [mm] |
10 |
50 |
100 |
r' = 10 |
0,12 |
0,59 |
1,18 |
r' = 110 |
1,29 |
6,47 |
12,94 |
Na podstawie obliczeń wywnioskowano, że dr'Δh jest wprost proporcjonalne do deniwelacji terenu i odległości od środka zdjęcia - promienia radialnego.
Wyszukiwarka
Podobne podstrony:
sprawozdanie nr 8, Geodezja i szacowanie nieruchomości niestacjonarne Olszyn, RoK III, sem.IV, sem.V
wsztstko na fotka(1), Geodezja, rok 3, Fotogrametria i teledetekcja, na 1 koło
Fotogrametria i teledetekcja
Fotogrametria i teledetekcja 3, uczelnia, BL, Geodezja, zagadnienia z geodezji
TiF opracowanie, Geodezja, semestr VI, Fotogrametria i teledetekcja II
FOTOGRAMETRI ŚCIĄGA NA KOLOS, Fotogrametria i teledetekcja
Fotogrametria i teledetekcja 2, uczelnia, BL, Geodezja, zagadnienia z geodezji
Fotogrametria i teledetekcja 4, uczelnia, BL, Geodezja, zagadnienia z geodezji
spr 2, Geodezja, rok 3, Fotogrametria i teledetekcja, sprawko nr 6 aerosys
testy 1, test-Fotogrametria i Teledetekcja
sciaga fotogrametria, Teledetekcja -
Egzamin z Fotogrametrii i Teledetekcji
fotka sc-moje, Geodezja, Fotogrametria
Temat4 formularz, Geodezja, semestr V, Fotogrametria i teledetekcja, Temat 2
pyt egz calosc, Geodezja, semestr VI, Fotogrametria i teledetekcja II
Fotka-sciaga-zadania 1, Geodezja, Fotogrametria, Egzamin
więcej podobnych podstron