Hrynczyszyn Grzegorz 13.11.1996r.

Niepsuj Andrzej

ĆWICZENIE 54

BADANIE ZJAWISKA REZONANSU

ELEKTROMAGNETYCZNEGO

1. Wstęp teoretyczny.

Rezonansem elektromagnetycznym szeregowym nazywamy występowanie maksymalnej amplitudy natężenia prądu dla określonej pulsacji siły elektromotorycznej , wymuszającej przepływ prądu w obwodzie. Rezonans elektromagnetyczny szeregowy zachodzi w szeregowo połączonych elementach R,L,C zasilanych napięciem sinusoidalnym zmiennym. Cechą charakterystyczną rezonansu szeregowego ( napięć ) jest całkowite kompensowanie się napięć na cewce i kondensatorze. Częstotliwość przy której następuje rezonans nazywamy częstotliwością rezonansową . Tłumiąca rola rezystancji w obwodzie RLC jest związana z rozproszeniem energii w postaci ciepła Joule'a. Dobroć obliczamy z zależności ;

Pulsacja przy której występuje rezonans , nazywa się pulsacją rezonansową.

2. Układ pomiarowy.

a. woltomierz elektroniczny V 621

b. multimetr cyfrowy V 562

c. generator akustyczny

d. obwód RLC

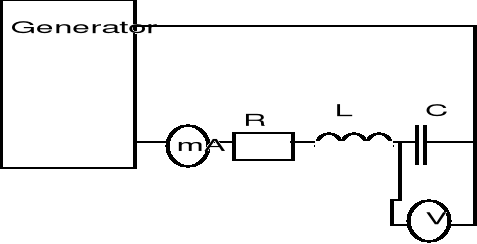
3. Tabele pomiarowe.

a. tabele i wykresy dla różnych wartości rezystancji R,a dla tej samej pojemności C.

Uwg	f	IR1	IR2	UC dla R1	UC dlaR2
V	kHz	mA	mA	V	V
2	7.3	4.6	4.6
2	7.5	4.7	4.6
2	7.7	4.7	4.6
2	7.9	5.0	5.1
2	8.1	6.0	6.2
2	8.3	8.4	8.6
2	8.5	12.9	14.8
2	8.6	17.1	23.1
2	8.7	21.0	34.1	38	60
2	8.8	20.6	30.9
2	8.9	17.6	22.0
2	9.1	12.0	13.1
2	9.3	9.0	9.4
2	9.5	7.3	7.5
2	9.7	6.5	6.5
2	9.9	5.8	5.9
2	10.1	5.2	5.3
2	10.3	4.9	4.9
2	10.5	4.7	4.7

I	f	Uc	Cv	Uc	Q		uwagi
mA	kHz	dz	V/dz	mV			R1 i C1
2.0	10.00	25	0,001	0.025	1,2E-06	62832
2.6	6.00	26	0,01	0.26	0,00013	37700
4.3	4.50	21	0,1	2.1	0,001	28275
7.2	3.90	13	0,1	1.3	0,00065	24505
8.2	3.80	16	0,1	1.6	0,0008	23877
9.6	3.70	19	0,1	1.9	0,00096	23248
11.6	3.60	24	0,1	2.4	0,0012	22620
14.8	3.50	10	1	10.0	0,005	21992
16.2	3.45	11	1	11.0	0,0055	21677
19.4	3.40	14	1	14.0	0,007	21363
20.8	3.35	15	1	15.0	0,0075	21049
22.8	3.30	17	1	17.0	0,0085	20735
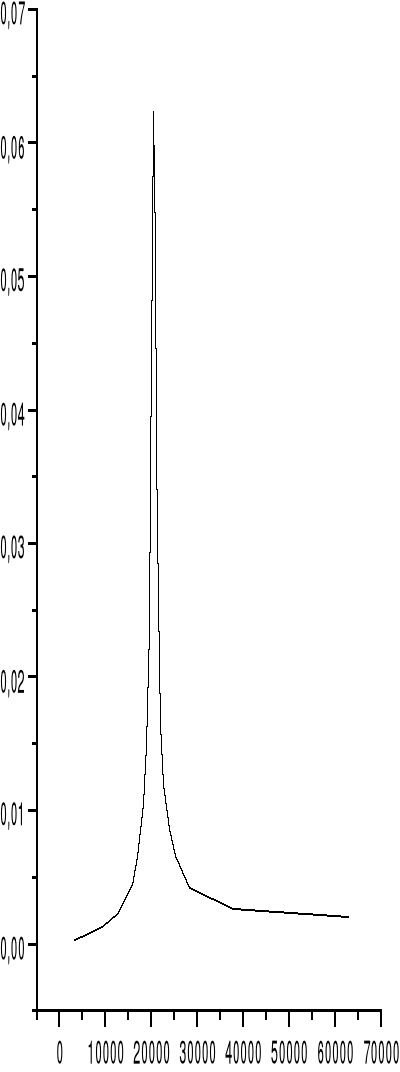
23.4	3.25	18	1	18.0	0,009	20421	fo
22.1	3.20	17	1	17.0	0,0085	20107
19.1	3.15	15	1	15.0	0,0075	19793
16.1	3.10	13	1	13.0	0,0065	19478
13.8	3.05	11	1	11.0	0,0055	19164
11.7	3.00	10	1	10.0	0,005	18850
9.5	2.90	27	0,1	2.7	0,0013	18222
7.2	2.80	21	0,1	2.1	0,00105	17593
6.1	2.70	19	0,1	1.9	0,00096	16965
5.1	2.60	16	0,1	1.6	0,0008	16337
2.2	2.00	30	0,1	3.0	0,0015	12567
1.2	1.50	24	0,1	2.4	0,0012	9425
0.7	1.00	21	0,1	2.1	0,00105	6284
0.3	0.50	19	0,1	1.9	0,00095	3142
1.3	1.50	25	0.1	2.5	0.0012	9425
0.7	1.00	21	0.1	2.1	0.0010	6284
0.3	0.50	19	0.1	1.9	0.0009	3142

* wykres dla R3 i C1

b. tabele pomiarów i wykresy dla różnych pojemności C , a takiej samej rezystancji R.

I	f	Uc	Cv	Uc	Q		uwagi
mA	kHz	dz	V/dz	mV
2.4	15.0	44	0.01	0.44	0.0002	94248	R1 i C2
2.5	10.0	12	0.1	1.2	0.0006	62832
6.1	7.0	68	0.1	6.8	0.0034	43983
11.3	6.5	4	1	4.0	0.0020	40841
14.7	6.4	20	1	20.0	0.0100	40213
18.6	6.3	26	1	26.0	0.0130	39585
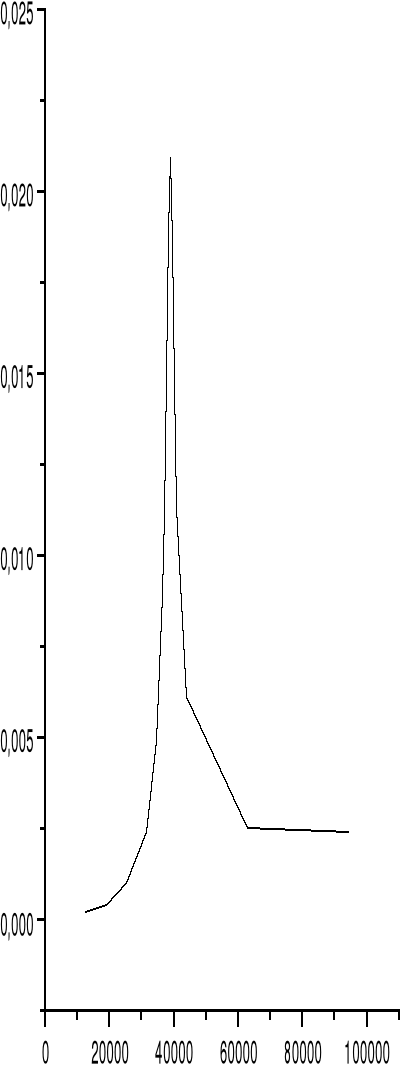
20.9	6.2	30	1	30.0	0.0150	38956	fo
18.9	6.1	28	1	28.0	0.0140	38328
14.9	6.0	23	1	23.0	0.0135	37700
11.1	5.9	18	1	18.0	0.0090	37071
8.9	5.8	15	1	15.0	0.0075	36443
4.9	5.5	92	0.1	9.2	0.0046	34558
2.4	5.0	56	0.1	5.6	0.0028	31416
1.0	4.0	33	0.1	3.3	0.0016	25133
0.4	3.0	25	0.1	2.5	0.0012	18850
0.2	2.0	22	0.1	2.2	0.0011	12567

* wykres dla R1 i C2

I	f	Uc	Cv	Uc	Q		uwagi
mA	kHz	dz	V/dz	mV
2.7	15.0	10	0.1	1.0	0.0005	94248	R1 i C3
4.0	10.0	50	0.1	5.0	0.0025	62832
8.1	9.0	13	1	13.0	0.0065	56549
13.4	8.7	25	1	25.0	0.0125	54664
16.7	8.6	30	1	30.0	0.0150	54036
19.0	8.5	37	1	37.0	0.0185	53408
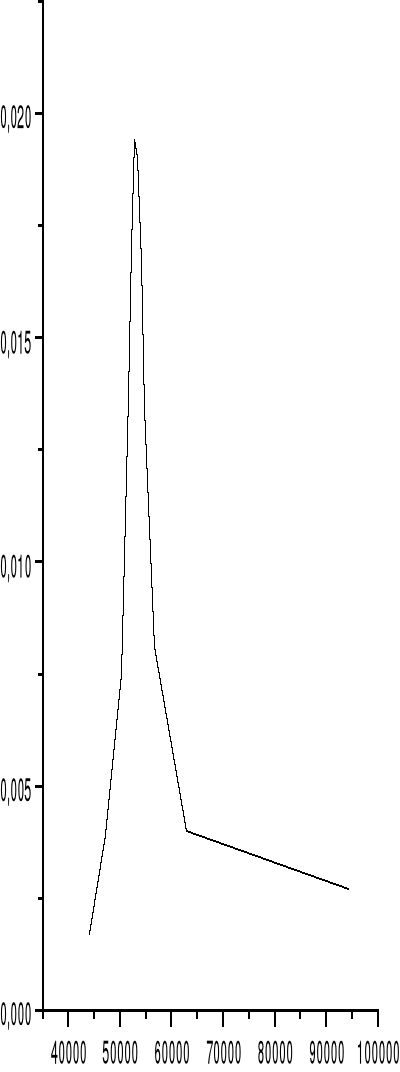
19.4	8.4	40	1	40.0	0.0200	52779	fo
17.0	8.3	36	1	36.0	0.0180	52151
13.7	8.2	30	1	30.0	0.0150	51523
10.1	8.1	24	1	24.0	0.0120	50894
7.5	8.0	18	1	18.0	0.0090	50266
3.9	7.5	94	0.1	9.4	0.0047	47124
1.7	7.0	64	0.1	6.4	0.0032	43983

* wykres dla R1 i C3

4. Obliczenia.

a. obliczanie dobroci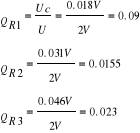

b. wyznaczenie częstotliwości rezonansowych

dla R1 , R2 ,R3 i C1 fo = 3250 Hz

dla C2 i R1 fo = 6200 Hz

dla C3 i R1 fo = 8400 Hz

c. obliczanie indukcyjności cewki ( przy znanej częstotliwości fo = 3250 Hz oraz znanej pojemności C1= 69 nF )

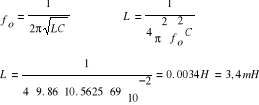
5. Wykres krzywej rezonansowej.

maximum record size = 132 record size = 262144
6. Wnioski.

O rezonansie decydują oprócz częstotliwości napięcia zasilającego tylko parametry L i C obwodu , rezonans można osiągnąć przez zmianę tych parametrów . Rezystancja nie wpływa na fakt powstawania rezonansu ma znaczenie tylko jako czynnik ograniczający wartość prądu i wpływa na kształt charakterystyki prądowej . Im mniejsza jest rezystancja R tym większy jest prąd rezonansowy . W czasie rezonansu reaktancja zastępcza obwodu X jest równa zero. Dobroć jest największa podczas rezonansu i zmniejsza się w miarę " oddalania " się od częstotliwości rezonansowej .

---