1. Teoria (Mieczkowski Łukasz)

Bryła sztywna to ciało, w którym pod wpływem działających sił zewnętrznych nie zmienia się wzajemna odległość pomiędzy cząsteczkami tego ciała (siły te nie zmieniają kształtu ciała). Z definicji wynika, że dane ciało czasami możemy traktować jak bryłę sztywną (wtedy, gdy działające siły są zbyt małe aby to ciało odkształcić), a innym razem, gdy działające siły są większe, ciało przestaje być bryłą sztywną.

Wyróżniamy dwa typy ruchów prostych bryły sztywnej: postępowy i obrotowy.

Ruch postępowy powstaje gdy na bryłę działa siła powodująca powstanie przyspieszenia.

O tym ruchu mówi nam pierwsza i druga zasada dynamiki Newtona. Podobnie jest z ruchem obrotowym, o którym mówi pierwsza i druga zasada dynamiki Newtona dla ruchu obrotowego.

I zasada dynamiki- istnieje taki układ odniesienia, w którym jeżeli na ciało nie działają siły zewnętrzne, lub działające siły równoważą się, to ciało pozostaje w spoczynku, lub porusza się ruchem jednostajnym prostoliniowym.

I zasada dynamiki ruchu obrotowego- W inercjalnym układzie odniesienia bryła nie obraca się lub obraca się ruchem jednostajnym (w= const), gdy nie działają na nie żadne momenty sił lub gdy działające momenty sił się wzajemnie równoważą.

Warunek równowagi:

Bryła może nie obracać się ale przesuwać ruchem postępowym. Dlatego łączne spełnienie warunków równowagi dla obu rodzajów ruchu (postępowego i obrotowego) daje pewność, że bryła pozostaje w spoczynku (lub ruchu jednostajnym):

II zasada dynamiki Newtona- przyspieszenie ciała jest wprost proporcjonalne do wypadkowej siły działającej na to ciało i ma kierunek zgodny z kierunkiem siły oraz dla danej siły przyspieszenie jest odwrotnie proporcjonalne do masy ciała.

II zasada dynamiki ruchu obrotowego- jeśli na pewne ciało, które posiada pewien swój moment bezwładności I zadziałają zewnętrzne siły, które wywrą na to ciało pewien wypadkowy moment siły M, to w wyniku tego działania ciało będzie obracać się z przyspieszeniem kątowym, Błąd! Nie zdefiniowano zakładk,i.takim że:

Moment siły- Moment M siły działającej na ciało to wielkość wektorowa określona przez iloczyn wektorowy działającej siły i promienia. Wektor momentu siły jest prostopadły do płaszczyzny wyznaczonej przez wektor siły i wektor r, a jego zwrot określa reguła śruby prawoskrętnej. Zgodnie z tą regułą, jeśli będziemy obracali po najkrótszej drodze pierwszy wektor (tu: r) tak, aby pokrył się z drugim (tu: F), to obracana w tym samym kierunku śruba prawoskrętna będzie przesuwać się (będzie wkręcana lub wykręcana) w kierunku określającym zwrot wektora M

Moment pędu- Moment pędu to iloczyn wektorowy dwóch wektorów. Wektora położenia i wektora pędu. Wartość momentu pędu jest to iloczyn wartości wspomnianych wektorów i sinusa kąta między nimi. Wektor momentu pędu jest prostopadły do płaszczyzny, na której leżą wektor położenia i pędu.
Dla bryły sztywnej moment pędu to iloczyn prędkości kątowej i momentu bezwładności bryły.

Zasada zachowania momentu pędu- jeżeli na ciało lub układ ciał wypadkowy układ działających sił jest równy 0, to :


Moment pędu bryły sztywnej:

Moment bezwładności- wielkość(I_a)opisująca rozkład masy względem osi obrotu, równa sumie iloczynów mas wszystkich n punktów materialnych układu i kwadratów ich odległości od osi. Moment bezwładności ciała równy jest:

gdzie dm = r dV jest masą małego elementu objętości bryły dV,

p - gęstością, a r - odległością elementu dV od osi a.

Wielkości charakterystyczne dla były sztywnej

Ruch postępowy	Ruch obrotowy
Prędkość v= Przyspieszenie- = Siła- F= ma Pęd- p= mv	Prędkość kątowa- ω= Przyspieszenie kątowe- ε= Moment siły- M(F)= Fw x R Moment bezwładności- I = M(F)= Iε Moment pędu- L= Iω M(F)=
s- droga t- czas m- masa
		φ- droga kątowa

Zależności między prędkością liniową a kątową

s= ϕ r v= ωr

s-droga w ruchu liniowym

v-prędkość w ruchu liniowym

Przyspieszenie kątowe- pochodna prędkości kątowej po czasie lub druga pochodna drogi kątowej po czasie.

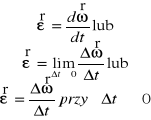
Wyprowadzenie wzoru

Wyprowadzanie wzoru na moment bezwładności należy zacząć od wzoru na energie potencjalną i prawa zachowania energii, ponieważ opadający ciężarek będzie wykorzystywał tą zasadę przy opadaniu

Energia potencjalna E= m g h

Zasada zachowania energii mgh=
mv² +
lω²

Prędkość v=
x

Droga s=h=

x t²

Stąd
=

Z zależności między drogą kątową i liniową otrzymujemy

ω=

Po podstawieniu do zasady zachowania energii otrzymujemy wzór:

I=

2. Praktyka

1. Zmierzyć suwmiarką promień walca.

2. Zmierzyć odległość h.

3. Nawinąć sznurek na walec.

4. Puścić krzyżak swobodnie i zmierzyć czas jego opadania t.

5. Obliczyć z wyprowadzonego wzoru.

I=

6. Sporządzić wykres zależności momentu bezwładności od położenia obciążników.

7. Przeprowadzić dyskusję błędów.

lp	L	m	r	h	t1	t2	t3	tśr	I
		[m]	[kg]	[m]	[m]	[s]	[s]	[s]	[s]	[kg*m^2]	dI
1	0,16956	0,2	0,0075	0,71	15:81	15:29	15:50	15:53	0,0186	0,0003
2	0,15256	0,2	0,0075	0,71	14:09	14:72	13:81	14:54	0,0163	0,0003
3	0,13056	0,2	0,0075	0,71	11:09	11:69	11:22	11:33	0,0099	0,0002
4	0,12056	0,2	0,0075	0,71	10:11	10:55	10:61	10:42	0,0084	0,0002
5	0,10056	0,2	0,0075	0,71	9:53	9:65	9:40	9:53	0,0070	0,0001
6	0,09056	0,2	0,0075	0,71	8:94	9:20	9:19	9:11	0,0064	0,0001
7	0,08056	0,2	0,0075	0,71	8:69	8:00	8:43	8:37	0,0054	0,0001
8	0,07056	0,2	0,0075	0,71	7:18	7:43	7:63	7:41	0,0042	0,0001
9	0,06056	0,2	0,0075	0,71	6:75	6:70	6:94	6:80	0,0036	0,0001
10	0,05056	0,2	0,0075	0,71	6:23	6:06	6:32	6:20	0,0030	0,0001

Dyskusja błędów

Błędy przy pomiarze

Δh= 0,001m - metrówka

Δr= 0,00001m - suwmiarka

Δt =0,2s - stoper

Niepewność typu B

dI=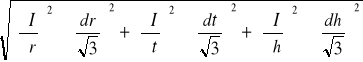

Pochodne cząstkowe

Wartości pochodnych i niepewność typu B

L[m]				dI
0,16956	4,99046	0,00241	0,02637	0,0003
0,15256	4,37411	0,00226	0,02312	0,0003
0,13056	2,65478	0,00176	0,01404	0,0002
0,12056	2,24499	0,00162	0,01187	0,0002
0,10056	1,87738	0,00148	0,00993	0,0001
0,09056	1,71529	0,00141	0,00908	0,0001
0,08056	1,44747	0,00130	0,00766	0,0001
0,07056	1,13383	0,00115	0,00600	0,0001
0,06056	0,95436	0,00106	0,00506	0,0001
0,05056	0,79287	0,00096	0,00420	0,0001

---