Marta Miller

Rok 1, gr.4, Budownictwo

Ćwiczenie 64

Wyznaczanie zależności współczynnika załamania światła od

stężenia roztworu za pomocą refraktometru Abbego

1. Celem doświadczenia jest pomiar zależności współczynnika załamania światła od stężenia roztworów, następnie opierając się na tych zależnościach, wyznaczyć stężenie roztworu znając jego współczynnik załamania światła.
   Współczynnik załamania 7 roztworów o danym stężeniu oraz roztworu X wyznaczamy za pomocą refraktometru Abbego.

2. Główną częścią refraktometru są 2 prostokątne pryzmaty - oświetlający P1 i pomiarowy P2, wykonane ze szkła o dużym współczynniku załamania. Między pryzmaty wprowadzamy kilka kropel badanej cieczy, której współczynnik załamania jest mniejszy niż współczynnik załamania szkła pryzmatów. Ciecz tworzy między pryzmatami cienką warstewkę, pryzmat P1 jest oświetlany białym światłem rozproszonym, które pada pod różnymi kątami na powierzchnię graniczną między cieczą i szkłem. Do cieczy przechodzą tylko promienie, których kąt padania jest większy od kąta granicznego, promienie idące dalej doznają w warstwie cieczy przesunięcia i biegną przez pryzmat P2. Następny pryzmat P3 zmienia kierunek promieni i docierają one przez układ pryzmatów P4 iP5 do lunetki. W wyniku zjawiska wewnętrznego odbicia na przeciwprostokątnej powierzchni pryzmatu P1, część pola widzenia w lunetce jest oświetlona, a część ciemna. Obracając pryzmat P3 zmieniamy położenie linii rozgraniczającej pola ciemne i pole oświetlone (do pomiaru ustawiamy tę linię na przecięciu nici pajęczych widocznych w okularze lunety) Z pryzmatem P3 połączona jest podziałka, na której odczytujemy wartość współczynnika załamania cieczy.

3. Mierzymy współczynnik załamania cieczy dla wody destylowanej, a następnie dla roztworów gliceryny o innych stężeniach oraz dla roztworu o nieznanym stężeniu - X. Na podstawie wykonanych pomiarów dla roztworów o znanych stężeniach określamy zależności współczynnika załamania światła od stężenia cieczy, a następnie znając te zależności określamy stężenie roztworu X znając jego współczynnik

Obliczenia :

Kąt graniczny liczymy ze wzoru: sin

dla wody destylowanej :

n₁=1,3320

=1,3321 n_śr= 1,3320
48,66°

=1,3319

dla roztworu 0,05 [g/cm]

n₁=1,3379

n₂=1,3376 n_śr=1,3378
48,37°

n₃=1,3378

dla roztworu 0,100 [g/cm]

n₁=1,3442

n₂=1,3443 n_śr=1,3443
48,06°

n₃=1,3444

dla roztworu 0,150 [g/cm]

n₁=1,3460

n₂=1,3458 n_śr=1,3458
48,00°

n₃=1,3457

dla roztworu 0,20 [g/cm]

n₁=1,3564

n₂=1,3562 n_śr=1,3563
47,50°

n₃=1,3563

dla roztworu 0,25 [g/cm]

n₁=1,3622

n₂=1,3621 n_śr=1,3621
47,24°

n₃=1,3620

dla roztworu 0,30 [g/cm]

n₁=1,3659

n₂=1,3653 n_śr=1,3654
47,09°

n₃=1,3652

dla roztworu X [g/cm]

n₁=1,3475

n₂=1,3476 n_śr=1,3476
47,91°

n₃=1,3477

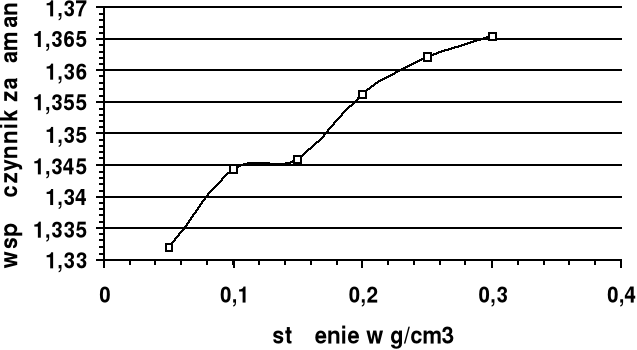
Rysujemy wykres zależności współczynnika załamania od stężenia roztworu - n=f(c).

Na podstawie wykresu określamy nieznane stężenie c_x roztworu, którego współczynnik załamania zmierzyliśmy. Wynosi ono około 0,150 g/cm³.

RACHUNEK BŁĘDÓW:

Δn = max|n-n_i| - błąd pomiaru:

-Dla wody destylowanej

Δn=1,3320-1,3319=0,0001

-Dla gliceryny o stężeniu 0,05 g/cm³

Δn=1,3378-1,3376=0,0002

-Dla gliceryny o stężeniu 0,1 g/cm³

Δn=1,3443-1,3442=0,0001

-Dla gliceryny o stężeniu 0,15 g/cm³

Δn=1,3458-1,3460=0,0002

-Dla gliceryny o stężeniu 0,2 g/cm³

Δn=1,3563-1,3562=0,0001

-Dla gliceryny o stężeniu 0,25 g/cm³

Δn=1,3621-1,3620=0,0001

-Dla gliceryny o stężeniu 0,3 g/cm³

Δn=1,3654-1,3659=0,0005

-Dla gliceryny o stężeniu x g/cm³

Δn=1,3476-1,3475=0,0001.

Wnioski :

Ćwiczenie to potwierdziło prawa odbicia i załamania światła. Dzięki nim właśnie mogliśmy dokonywać wszystkich w/w pomiarów. Ponadto do wyznaczenia współczynnika załamania ośrodka wykorzystaliśmy zjawiska rozszczepienia i całkowitego wewnętrznego odbicia światła.

Wraz ze wzrostem stężenia wzrasta również współczynnik załamania n , a kąt graniczny maleje , gdyż jest on odwrotnie proporcjonalny do współczynnika n .

Dzięki narysowaniu wykresu mogliśmy odczytać prawdopodobne stężenie ostatniego roztworu.

Błędy w odczycie wynikają głównie z niedoskonałości zmysłów obserwatora. Pomiary mogę uznać za poprawne ponieważ wyszły małe błędy.

---