Akademia Górniczo-Hutnicza

im. Stanisława Staszica

Wydział Inżynierii Mechanicznej I Robotyki

Podstawy automatyki - laboratorium

Rozwiązywanie równań różniczkowych z niezerowymi warunkami początkowymi

Wykonali:

Łabusiewicz Jacek

Latacz Andrzej

Rok 2, Grupa 7

Cel ćwiczenia:

• Zapoznanie się z różnymi metodami rozwiązywania równań różniczkowych w programie „Matlab”,

• Wykorzystywanie modułu „Simulink” do tworzenia modelu równania różniczkowego,

• Wykorzystywanie funkcji Matlab`a do rozkładania transmitancji na ułamki proste.

Przebieg ćwiczenia:

1. Rozwiązanie równania różniczkowego:

• Analitycznie:

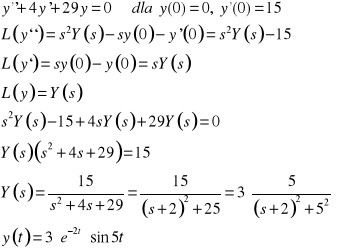
• W programie Matlab:

Wykorzystanie funkcji ode45

m - pliki potrzebne do rozwiązania tego równania:

• Główny:

function rozw1

t0=0;

clc

disp('Funkcja rozwiazuje rownanie rozniczkowe zwyczajne metoda ');

disp('Rungego - Kutty i podaje jego interpretacje graficzna:');

disp(' ');disp('Postac rownania:');disp(' ');

disp(' y``+ 4.*y`+ 29.*y = 0');

x01=input ('Podaj wartosc y01 = ');

x02=input ('Podaj wartosc y02 = ');

tk=input ('Podaj czas symulacji tk = ');

x0=[x01 x02];

[t,x]=ode45('funkcja1',t0,tk,x0,0.001,0);

plot(t,x(:,1),'r-');

xlabel('czas [s]');ylabel('amplituda sygnalu');

title('Wykres rozwiazania rownania rozniczkowego');

grid;

• Funkcyjny:

function xdot=funkcja1(t,x)

% Układ rownan rozniczkowych

xdot=zeros(2,1);

xdot(1)=x(2);

xdot(2)=(-29*x(1)-4*x(2));

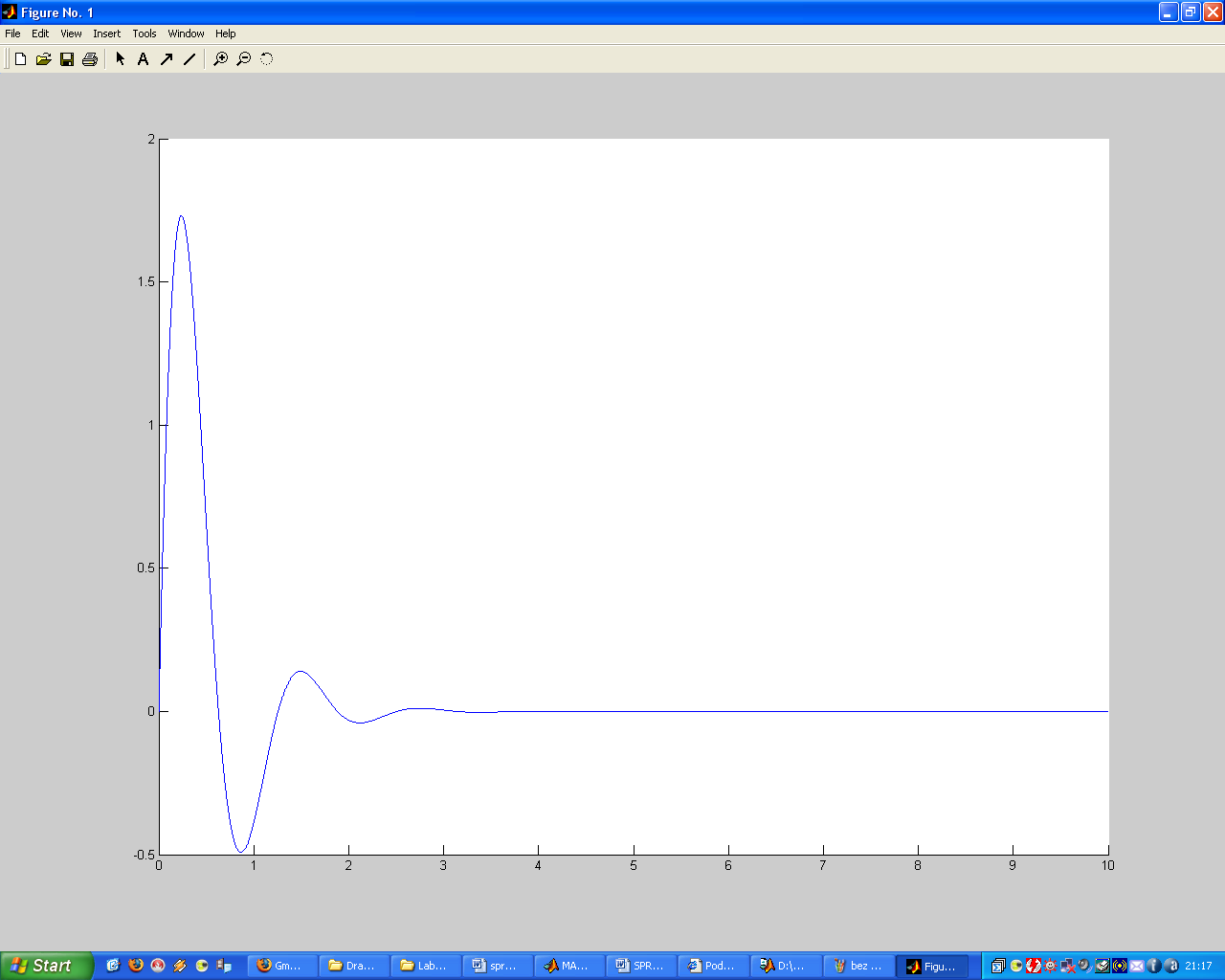
Wykres rozwiązana dla t = 10 [s]:

• Rozwiązanie równania z wykorzystaniem SIMULINK`a:

model:

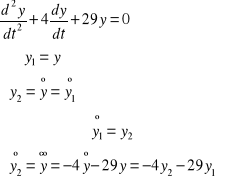
Wnioski:

Metody numeryczne pozwalają na rozwiązywanie równań różniczkowych mniejszym nakładem czasu i pracy, dając przy tym wyniki zbliżone do rzeczywistych. Różnice między wynikami rzeczywistymi a wynikami uzyskanymi za pomocą Matlab`a lub Simulink`a, są na tyle małe że z reguły można je pominąć w dalszej analizie. Do wyników z metody analitycznej, najbardziej zbliżone są wyniki z Matlab`a, natomiast wyniki otrzymane przy użyciu Simulink`a są najmniej dokładne.

---