ROLE WYPOWIEDZI

Rola opisowa - pełnią przede wszystkim zdania oznajmujące, polega na tym iż wypowiedz służy do opisu że tak a tak jest lub tak a tak nie jest,

Rola sugestywna - polega na tym że wypowiedz ma skłaniać odbiorcę do określonego postępowania. Zdania rozkazujące, prośby, życzenia, itp.,

Rola ekspresyjna - polega na tym że wypowiedz służy do wyrażania czyjegoś stanu emocjonalnego bądź intelektualnego,

Rola performatywna - polega na tym że przez wypowiedzenie pewnych słów w określonej sytuacji dokonuje się określonej czynności kulturowej, np. przebaczenia, obiecania.

NAZWY

I)

1. proste - składają się tylko z jednego wyrazu,

2. złożone - składają się z więcej niż jednego wyrazu,

II)

1. konkretne - takie nazwy które są znakami rzeczy („stół”) albo osób („sędzia”), ewentualnie czegoś co wyobrażamy sobie jako rzecz lub osobę („kwiat paproci”, „nimfa”):

• gdy ma desygnat (1 lub więcej)

• gdy nie ma desygnatu ale wyobrażamy to sobie,

• gdy jest rzeczą, osobą ...,

abstrakcyjne - takie nazwy które nie są znakami rzeczy czy osób ani czegoś, co sobie jako rzecz czy osobę wyobrażamy. Wskazują one na pewną cechę wspólną wielu przedmiotów („białość”), na pewne zdarzenia czy stany rzeczy („płacz”, „kradzież”) albo na pewien stosunek między przedmiotami („braterstwo”, „wyższość”),

III)

1. indywidualna - wskazuje na desygnat jako na coś co jest tak a nie inaczej nazywane bez względu na swoje cechy,

2. generalna - wskazuje na desygnat jako na coś co posiada określony zespół cech,

IV)

1. ogólne - więcej niż jeden desygnat,

2. jednostkowe - 1 desygnat,

3. puste - brak desygnatu,

V)

1. zbiorowa - nazwy, których desygnatami są nie poszczególne rzeczy, lecz takie przedmioty, które traktujemy jako agregaty złożone z poszczególnych rzeczy,

2. nie zbiorowa -

VI)

1. ostra - jeśli umiemy bez wątpliwości rozstrzygnąć o każdym napotkanym przedmiocie, z którym odpowiednio się zapoznaliśmy, czy jest on, czy nie jest desygnatem pewnej określonej nazwy,

2. nie ostra - jeśli o pewnych napotkanych przedmiotach, mimo dobrego zapoznania się z ich cechami, nie umiemy orzec, czy są, czy nie są desygnatami danej nazwy.

Supozycja

1. prosta - gdy jest jeden desygnat,

2. formalna - wyraz może być nazwą dla całego gatunku przedmiotów, dla oznaczenia całej klasy desygnatów tej nazwy,

3. materialna -

DEFINICJA

I)

1. sprawozdawcza - wskazuje, jakie znaczenie ma, czy też miał kiedyś definiowany wyraz w pewnym języku. Ma odtwarzać takie znaczenie wyrazu, jakie ma on w danym języku,'

2. projektująca - ustala znaczenie jakiegoś słowa na przyszłość, w projektowanym sposobie mówienia:

1. konstrukcyjna - definiowanie nowopowstałej rzeczy, lub istniejącej ale na nowo definiowanej ze względu na nowe cechy - „płaszczynka”, „sól”,

2. regulująca - definicja która została stworzona w celu uregulowania zakresu słowa definiowanego - „rzeka”, „struga”,

II)

1. realna - zdanie podające taką charakterystykę pewnego podmiotu czy też przedmiotów jakiegoś rodzaju, którą tym i tylko tym przedmiotom można przypisać - „człowiek jest istotą rozumną, istotą zdolną do abstrakcyjnego myślenia, czy istota umiejącą wytwarzać narzędzia” - pierwszego stopnia = A ma cechy B, C, D,

2. nominalna - wyrażenie w ten czy inny sposób podające informacje o znaczeniu jakiegoś słowa czy słów (słów definiowanych). Podaje informacje o znaczeniu definiowanego słowa - Wyraz „deltoid” znaczy tyle co „czworokąt p dwóch parach przyległych boków równych” - drugiego stopnia = A jest to B mające cechę C,

III)

1. równościowa - definiendum + łącznik + definiens,




2. klasyczna:

{znaczy}

A {oznacza} B o cechach C,

{jest to}

3. nieklasyczna:

{znaczy}

A {oznacza} B lub C, lub D,

{jest to}

• słownikowa - „Definiendum” łącznik „Definiens”,

• semantyczna - „Definiendum” łącznik Definiens,

• przedmiotowa - Definiendum łącznik Definiens,

2. nierównościowe - zdarzenia to nie cechy a cechy to nie zdarzenia.

BŁĘDY W DEFINICJACH

1. ignotum per ignotum - „nieznane przez nieznane”

2. idem per idem - „to samo przez to samo”,

3. definicja za szeroka - jeśli zakres definiensa obejmuje jakieś przedmioty nie należące do zakresu definiendum,

4. definicja za wąska - jeśli zakres definiensa nie obejmuje jakiś przedmiotów należących do zakresu definiendum,

5. błąd przesunięcia kategorialnego - definiens i definiendum wykluczają się,

6. błędne koło bezpośrednie - idem per idem,

7. błędne koło pośrednie - A definiujemy używając B, wyraz B zaś za pomocą wyrazu C, a w końcu okazuje się że ów wyraz C wymaga zdefiniowania za pomocą wyrazu A,

PODZIAŁ

Podział:

• desygnat nazwy N jest desygnatem jednej z nazw A, B, C, D,

• wskazanie dwóch lub więcej nazw, których zakresy są podrzędne względem zakresu dzielonego, czyli w obrębie poddanego podziałowi zakresu nazwy.

1. wyczerpujący - jeśli każdy z desygnatów nazwy, której zakres dzielimy, może być zaliczony do jakiegoś wyróżnionego człony podziału,

2. rozłączny - żaden z desygnatów nazwy, której zakres dzielimy, nie może być zaliczony do dwóch członów podziału na raz,

3. poprawny - ani a), ani b),

4. dychotomiczny według cech kontradyktorycznych - w obrębie zakresu dzielonego wyróżnia klasę przedmiotów posiadających pewną cechę i klasę przedmiotów, które tej cechy nie posiadają,

5. determinady - wyróżnia się człony podziału biorąc za podstawę jakąś ogólną cechę,

6. naturalny - bardziej chodzi o opis naukowy, gdy dzielimy według cech itp.,

7. sztuczny - bardziej chodzi o segregowanie przedmiotów, w małym stopniu wiążą się z tym jakieś cechy,

Klasyfikacja - dalszy podział zakresów otrzymanych jako człony pierwszego podziału logicznego,

Partycja - wyróżnienie części składowych pewnego przedmiotu.

ZDANIE

Zdanie w sensie logicznym - wyrażenie jednoznacznie stwierdzające, na gruncie danego języka, iż tak a tak jest albo że tak a tak nie jest.

• zdanie w sensie logicznym ma stwierdzać, że tak a tak jest albo że tak a tak nie jest,

• zdanie w sensie logicznym ma jednoznacznie stwierdzać coś określonego (jeżeli występują nazwy abstrakcyjne to nie jest to zdanie w sensie logicznym),

• spośród zdań w sensie gramatycznym zdania w sensie logicznym mogą być tylko zdaniami oznajmującymi.

Zdarzenie - fakt, że rzecz czy osoba A w momencie B wykazywała własność C, a w innym momencie B₁ tej własności nie wykazywała (lub na odwrót),

Stan rzeczy - fakt, iż rzecz czy osoba A w momencie w okresie od momentu B do momentu B₁ nieprzerwanie wykazywała własność C.

Wartość logiczna zdania:

Zdanie prawdziwe - jest to zdanie, które opisuje rzeczywistość taką jaka ona jest,

Zdania fałszywe - jest to zdanie, które opisuje rzeczywistość niezgodnie z tym jak się ona ma.

Rodzaje zdań:

Zdanie analityczne - prawdziwość jest przesądzona ze względu na samo znaczenie użytych w mich słów,

Zdanie wewnętrznie kontradyktaryczne - fałszywość jest przesądzona ze względu na samo znaczenie użytych w nim słów,

Zdanie syntetyczne - trzeba szukać sprawdzianów, czy to, co one głoszą, odpowiada rzeczywistości, jakiegoś probierza prawdziwości,

Zdanie egzystencjalne - zdanie orzekające o istnienie (nie istnieniu) przedmiotów jakiegoś rodzaju.

Wypowiedz zdaniowa niezupełna - wyrażenie, które w prawdzie na gruncie danego języka nie jest zdaniem w sensie logicznym, lecz a tyle spełnia rolę zdania w sensie logicznym, o ile słuchacz zdaje sobie sprawę z pewnych domyślnych uzupełnień wypowiedzi, pominietych przez mówiącego.

Kwantyfikator ogólny:

Jeśli x jest żółte, to x jest kolorowe - prawda,

Jeśli x jest kolorowe, to x jest żółte - fałsz,

Kwantyfikator szczegółowy:

x jest kolorowe i x jest żółte,

Funkcje:

„każde S jest P”

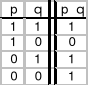
„jeśli p, to q”

Zdanie złożone - zdanie w obrębie którego występuje część będąca odrębnym zdaniem.

Zdanie proste (kategoryczne) - zdanie w obrębie którego nie występuje część będąca odrębnym zdaniem:

„a jest b”

„a ma własność b”

Zdanie atomiczne - orzekające, że jakieś indywiduum x, określona jednostka oznaczona nazwą indywidualną, przynależy do określonej klasy A - „x ∊ A”, - „Jan jest górnikiem”

Zdanie subsumpcyjne - orzekające, że jakaś klasa A w całości czy w części zawiera się (nie zawiera) w jakiejś klasie B - „pies jest kręgowcem”

Ogólne - orzekające o całej klasie S [„każde S jest (nie jest) ...”],

Szczegółowe - orzekające o niektórych S [„niektóre S są (nie są) ...”],

Twierdzące - „jest”,

Przeczące - „nie jest”

ogólno - twierdzące	Każde S jest P	S a P
ogólno - przeczące	Każde S nie jest P	S e P
szczegółowo - twierdzące	Niektóre S są P	S i P
szczegółowo - przeczące	Niektóre S nie są P	S o P

Wydanie sądu - ugruntowane przeświadczenie, że tak a tak jest lub tak a tak nie jest. Sąd jest przeżyciem, które jest odpowiednikiem zdań wypowiadanych „na serio” i z przekonaniem. Zdania służą przede wszystkim do wyrażania naszych sądów, choć nie z każdym formułowanym zdaniem łączy się sąd osoby mówiącej czy słuchającej takiej wypowiedzi.

Przypuszczenie - nie mamy ustalonego przeświadczenia, że tak jest (lub nie jest), jak głosi zdanie, lecz tylko skłonność do przyjmowania, że tak właśnie jest (lub nie jest).

Kłamstwo - wypowiedzenie jakiegoś zdania wbrew swym przeświadczeniom - co innego się myśli, a co innego podaje za prawdę.

Omyłka -

FUNKTORY PRAWIDŁOWOŚCIOWE

Funktor negacji

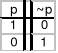
- matryca funktora prawidłowościowego, w tym przypadku przez dwa postulaty:

1) jeżeli funktor negacji uzupełnia się zdaniem fałszywym, powstaje zdanie fałszywe,

2) jeżeli funktor negacji uzupełnia się zdaniem fałszywym, powstaje zdanie prawdziwe

Funktor koniunkcji

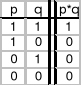
używa się także p∧q, Kpq

- fałszywość obu zdań składowych nie jest warunkiem koniecznym fałszywości koniunkcji, gdyż już przy jednym zdaniu fałszywym całość jest fałszywa.

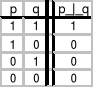
Funktor alternatywy nierozłącznej

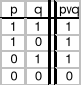
używa się też znaków p+q, Apq

- warunkiem wystarczającym prawdziwości alternatywy zwykłej jest prawdzi-wość choćby jednego argumentu zdaniowego. Natomiast warunkiem wystar-czającym fałszywości alternatywy zwykłej jest fałszywość obu zdań składowych.

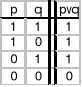
Funktor alternatywy rozłącznej (lub)

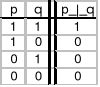
- zdanie złożone jest prawdziwe gdy jeden i tylko jeden z argumentów zdaniowych jest prawdziwy oraz jeden i tylko jeden jest fałszywy. Dla fałszywości alternatywy rozłącznej wystarcza, aby argument był tej samej wartości logicznej (oba prawdziwe albo oba fałszywe).

p ⊥ q ⇔ ~ (p ≡ q)

Funktor dysjunkcji (albo)

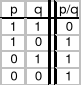
- zdanie złożone jest prawdziwe, jeśli przynajmniej jedno ze zdań składowych jest fałszywe. Prawdziwość obu zdań składowych jest warunkiem wystarczającym fałszywości dysjunkcji.

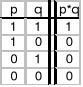
Funktor równoważności (funktor prawdziwościowy)

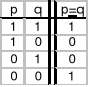
- zdanie złożone jest prawdziwe wtedy i tylko wtedy, gdy oba zdania składowe są tej samej wartości logicznej, fałszywe - jeśli zdania są odmiennej wartości logicznej,

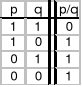
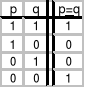
Funktor implikacji

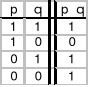
p ⊃ q

- implikacja jest fałszywa tylko wtedy gdy jej pierwsze zdanie (poprzednik) jest prawdziwe, a drugie (następnik) fałszywe.

p ⊃ q ^{d f} ~ (p ∙ ~q)

1. aby fałszem było zdanie p

2. aby prawdą było zdanie q

p ⊃ q ^{d f} ~ p v q

1. fałszywość poprzednika

2. prawdziwość następnika

NEGACJA

Para zdań względem siebie sprzecznych - jedno zdanie jest negacją drugiego zdania. Zdanie sprzeczne względem prawdziwego jest zdaniem fałszywym, a zdanie sprzeczne względem zdania fałszywego jest zdaniem prawdziwym.

Zasada sprzeczności głosi, że dwa zdania względem siebie sprzeczne nie mogą być oba prawdziwe,

Zasada wyłącznego środka głosi, że dwa zdania względem siebie sprzeczne nie mogą być oba fałszywe,

Zasada podwójnego przeczenia głosi, że negacja negacji jakiegokolwiek zdania ma taką samą wartość logiczną, jak owo zdanie, które zostało podwójnie zanegowane.

T₁ ~ (p∙ ~ p)

T₂ p v ~ p

T₃ p ≡ ~ (~ p)

Zdanie przeciwne

- „Piotr jest obecnie czynnym lotnikiem“

- „Piotr jest obecnie niewidomy”

na pewno nie są oba prawdziwe, ale nie jest wykluczone, że oba są fałszywe

- „Kruk jest biały”

- „Kruk jest czarny”

Zdanie sprzeczne

- „Piotr jest czynnym lotnikiem”

- „Nie jest tak, że Piotr jest czynnym lotnikiem”

KONIUNKCJA

„i” , „oraz” - spójniki międzyzdaniowe.

Znaczenie koniunkcyjne - A jest B i C, mając na myśli że A jest B i A jest C, tworząc część wspólną dla tych klas,

Znaczenie enumeracyjne - A i B są C, mając na myśli że przedmiot A należy do klasy C oraz przedmiot B należy do klasy C - a nie to że do tej klasy należą przedmioty będące zarazem przedmiotem A i przedmiotem B.

Aby je odróżnić można użyć „A i B zarazem”, „A oraz B”

Znaczenie syntetyzujące - A i B razem wzięte to C,

ALTERNATYWA NIEROZŁĄCZNA I ROZŁĄCZNA, DYSJUNKCJA

„lub” - spójnik międzyzdaniowy.

Nabywca otrzymał części zamienne lub bon na bezpłatną naprawę - otrzymał przynajmniej jedno, a nie wykluczamy że otrzymał i to i to.

„albo” - spójnik międzyzdaniowy.

Nabywca otrzymał części zamienne albo bon na bezpłatną naprawę - otrzymał jedno i tylko jedno z tych dwóch.

„bądź” - spójnik

Nabywca otrzymał bądź części zamienne, bądź bon na bezpłatną naprawę - nie otrzymał zarazem i części i bonu, co najwyżej jedno, a nie wyklucza się tego że i nie otrzymał części zamiennych, i nie otrzymał bonu.

IMPLIKACJA

Odpowiednik słowny „jeżeli ... to” (związek wynikania między zdaniami).

Sam odpowiednik słowny „Jeżeli to” to nie jest funktor prawdziwościowy, ale intencjonalny!!!

Jeżeli 2 zdania p i q tworzą prawdziwą implikację materialną, to mówimy, że zdanie p implikuje zdanie q.

Stosunek implikowania jest stosunkiem prawdziwościowym, tzn. zachodzi pomiędzy zdaniami tworzącymi prawdziwą implikacje materialną, niezależnie od treści tych zdań.

p - poprzednik implikacji

q - następnik implikacji.

WYNIKANIE

Wynikanie To stosunek między zdaniami.

Stosunek wynikania odmiennie niż stosunek implikowania nie jest stosunkiem prawdziwościowym.

Ze zdania Z₁ wynika zdanie Z₂ gdy zdanie Z₁ implikuje zdanie Z₂ a ponadto pomiędzy tym co głoszą te zdania zachodzi związek przesądzający, iż nie może być tak, że Z₁ jest prawdą a Z₂ fałszem. Aby określić stosunek wynikania trzeba znać treść tych zdań.

Funktor „Jeżeli...to” jest słownym odpowiednikiem stosunku wynikania.

Człony stosunku wynikania to:

1. racja

2. następstwo

RACJA: NASTEPSTWO:

prawdziwa prawdziwe

fałszywa fałszywe

Jeżeli racja jest 1 to następstwo musi być 1. Jest to związek przyczynowo skutkowy. Związek ten jest związkiem pomiędzy zdarzeniami, o których mówią te zdania.

• Związek strukturalny: „Jeżeli dzisiaj jest sobota to jutro jest niedziela.”

• Związek analityczny: „Jeśli Jan jest starszy od Pawła, to Paweł jest młodszy od Jana.”

• Zawiązek tetyczny: „Jeśli kto z winy swej wyrządził drugiemu szkodę, to wg. Art. 415 KC obowiązany jest do jej naprawienia.”

• Związek przyczynowy: „ jeśli długo padają deszcze, to gliniaste drogi stają się trudne do przebycia.”

WYNIKANIE TO IMLIKACJA ŚCISŁA.

WYPOWIEDZI MODALNE

Interpretacje „musi być A” i „może być A”

• Logiczna - odwołanie do zdań uprzednio przez nas uznanych jako prawdziwe

• Dynamiczna - do istniejącego układu czynników

• Aksjologiczna - do czyichś ocen

• Tetyczna - do obowiązujących w danej dziedzinie norm

• Psychologiczna - jesteśmy silnie przeświadczeni o tym, że A

Modalność - w jaki sposób zdania stwierdzają fakty

• Zdania asertoryczne - tak jest

• Zdania apodyktyczne - tak musi być

• Zdania problematyczne - tak może być

Zdanie apodyktyczne => zdanie asertoryczne => zdanie problematyczne

Modalność normatywna czynów

• Czyn nakazany (Nncx)

• Zakazany

• Dozwolony - nie jest zakazany

• Fakultatywny - nie jest nakazany

• Indyferentny - nie jest zakazany i nakazany

• Obowiązek - jeśli nie jest indyferentmy

PYTANIA I ODPOWIEDZI

Założenie pytania - twierdzeni, które zakłada się stawiając pytanie

Pytanie zamknięte - zostawia schemat udzielania odpowiedzi

Pytanie otwarte - brak schematu odpowiedzi

Pytanie do rozstrzygnięcia - domaga się wyboru jednej z danych odpowiedzi wykluczających się

Pytanie do uzupełnienia - domaga się zastąpienia niewiadomej pytania jakimś określonym wyrażeniem

Zakres niewiadomej pytania - klasa elementów, których nazwy można wstawić na miejsce niewiadomej pytania

Pytanie sugestywne - narzuca daną odpowiedź gdy nie jest on pewny

Odpowiedź właściwa - każde zdanie (prawdziwe czy fałszywe) powstałe przez zastąpienie partykuły pytajnej jakimś wyrażeniem należącym do zakresu niewiadomej pytania

Odpowiedź całkowita

• Wprost - stanowi odpowiedź właściwą na dane pytanie

• Nie wprost - nie jest odpowiedzią właściwą ale z której jakaś odpowiedź właściwa wynika

Odpowiedź częściowa - nie jest odpowiedzią właściwą to ma wartość informacyjną, że pewne odpowiedzi właściwe pozwala wykluczyć

PRZYCZYNY NIEPOROZUMIEŃ

Użycie homonimów (wieloznaczność słów)

Pomieszanie supozycji

Zwrot czasownikowy w znaczeniu aktualnym - dana czynność jest czy była wykonywana w tym momencie, w którym mówimy

Potencjalnym - w okresie czasu, który mamy na myśli ktoś czy coś ma zdolność do wykonywania danej czynności

Słowa okazjonalne - nie mają określonego stałego znaczenia; „ty”, „wtedy”

Błąd ekwiwokacji - osoba w jednym rozumowaniu używa słowa wieloznacznego w różnych znaczeniach, sądząc, że używa tego słowa jednoznacznie

Logomachia - spór słowny - dwóch ludzi spiera się o coś nie dostrzegając, że każdy z nich używa pewnego wieloznacznego słowa w innym jego znaczeniu

Błąd amfibologii - osoba wygłasza wypowiedź wieloznaczną ze względu na składnię, nie zdając sobie z tej wieloznaczności sprawy

Eufemizmy - wypowiedzi, które starają się złagodzić niemiłą treść

Błąd myślenia figuralnego - ktoś pewne zwroty obrazowe bierze w znaczeniu dosłownym

Skróty myślowe - „Jedź wolniej - dojedziesz szybciej”

WNIOSKOWANIE

Wnioskowanie jest to proces myślowy polegający na tym, że ktoś przyjmując pewne zdania lub kilka zdań za prawdziwe dochodzi na tej podstawie do przeświadczenia o prawidłowości innego zdania.

Przesłanka wnioskowania jest to te zdanie na podstawie którego uznajemy inne zdania za prawdziwe, czyli te zdania od których zaczyna się wnioskowanie.

Przesłanka entynematyczna - przemilczana, domyślna przesłanka czyjegoś wnioskowania.

WNIOSKOWANIE A WYNIKANIE

1) Wynikanie jest STOSUNKIEM.

2) Wnioskowanie jest ZDARZENIEM bądź CIĄGIEM ZDARZEŃ.

Wnioskowanie może być parte na wynikaniu, ale nie ma wnioskowania, które jest wynikaniem. Wnikanie jest obiektywne, tzn. niezależne od ludzkiej woli i wiedzy. Wnioskowanie jest subiektywne, tzn. zawsze czyjeś. Jest zależne od ludzkiej woli i wiedzy. Wnioskowanie można umieścić w czasie i przestrzeni, chociażby pośrednio (w czyjeś głowie). Wnikanie jest poza czasem i przestrzenią.

Racja } zdania, które łączy obiektywny Stosunek Wynikania

Następstwo }

Przesłanka }zdania, z których pierwsze, uznane przez kogoś za prawdziwe, jest dla tej

Wniosek }osoby podstawą uznania drugiego zdania za prawdziwe w akcie Wnioskowania

PRAWA LOGICZNE

Prawo logiczne (tautologia logiczna) - to funkcja zdaniowa, która po podstawieniach zawsze zmienia się w zdanie logiczne.

„stała logiczna” :

1. funktor ∊,

2. funktory prawdziwościowe,

3. kwantyfikatory,

4. wszelkie takie wyrażenia, które można zdefiniować, odwołując się jedynie do wyrażeń wymienionych poprzednio pod pozycjami 1 -3.

Funkcja logiczna - funkcja zdaniowa zbudowana jedynie ze stałych logicznych oraz ze zmiennych.

Prawo transpozycji: (p ⊃ q) ⊃ (~p ⊃ ~q)

• „Jeżeli pada deszcz, to jest mokro” implikujemy „Jeśli nie jest tak, że jest mokro, to nie jest tak że pada deszcz”,

• „Jeżeli Jan chrapie, to Jan śpi” implikujemy „Jeżeli Jan nie śpi, to Jan nie chrapie”,

• „Jeżeli rozważana liczba jest parzysta, to jest podzielna przez dwa” implikujemy „Jeżeli rozważana liczba nie jest parzysta, to rozważana liczba nie jest podzielna przez dwa”,

• „Bonaparte był Anglikiem ⊃ dwa razy dwa jest cztery” implikujemy „Nie jest tak, że dwa razy dwa jest cztery ⊃ nie jest tak, że Bonaparte był Anglikiem”.

Ponieważ: Jeżeli p, to q .

Więc: Jeżeli nie jest tak, że q, to nie jest tak, że p

Prawo kontrapozycji zdań typu SaP: ∏S,P : SaP ≡ nie-P a nie-S (nie zastąpić można ~),

• „Każdy samochód jest pojazdem” równoważne „Każdy nie-pojazd jest nie-samochodem”,

• „Każdy notariusz jest prawnikiem” równoważne „Każdy nie-notariusz jest nie-prawnikiem”,

• „Każdy słoń jest ptakiem” równoważne „Każdy nie-ptak jest nie-słoniem”.

Ponieważ: Jeżeli SaP .

Więc: nie-P a nie-S

WNIOSKOWANIE DEDUKCYJNE

Wnioskowanie dedukcyjne to takie wnioskowanie z którego przesłanek wynika logicznie jego wniosek.

• „Ponieważ: jeśli dziś jest tęgi mróz, to dziś jest lód na stawie, i dziś jest tęgi mróz - więc: dziś jest lód na stawie”

Ponieważ: jeżeli p, to q

i p .

Więc: q

ten schemat odpowiada prawu logicznemu zwanemu modus ponendo ponens:

T [(p ⊃ q) ∙ p] ⊃ q

We wnioskowaniu dedukcyjnym przesłanka czy koniunkcja przesłanek jest racją, a wniosek - następstwem logicznie wynikającym z tej racji: wnioskowanie przebiega tu zgodnie z kierunkiem wynikania. Prawo logiczne, według którego przebiega wnioskowanie, gwarantuje niezawodność wnioskowania dedukcyjnego: jeśli tylko w danym przypadku wnioskowania dedukcyjnego prawdziwe są przesłanki, to musi być prawdziwy i wniosek. Wnioskowanie dedukcyjne należy więc do wnioskowań niezawodnych.

Wnioskowanie dedukcyjne entymematyczne - takie wnioskowanie, w którym z wypowiedzianych przesłanek wniosek nie wynika logicznie, ale wynika logicznie z koniunkcji przesłanek wypowiedzianych i pewnych przesłanek domyślnych:

„Każdy władca jest człowiekiem”, „Każdy władca jest śmiertelny” to wnioskujemy dedukcyjnie lecz entymematycznie - ze względu na domyślną entymematyczną przesłankę iż „Każdy człowiek jest śmiertelny”.

ZAPRZECZENIE ZDANIOM ZŁOŻONYM

Pierwsze prawo de Morgana - negacja koniunkcji

T 4 Morg I ~(p∙q) ≡ (~p v ~q)

Ponieważ: nie jest tak, że zarazem p i q ,

Więc: nie jest tak, że p - lub - nie jest tak, że q. i odwrotnie.

Często popełnia się błąd utożsamiając negację koniunkcji (1) z koniunkcją negacji (2):

1. „Nieprawda, że zarazem Jan ukradł i Piotr ukradł”,

2. „Nieprawda, że Jan ukradł, i nieprawda, że Piotr ukradł”.

Drugie prawo de Morgana - negacja alternatywy.

T 5 Morg II ~(pvq) ≡ (~p ∙ ~q)

Ponieważ: nie jest tak, że: p lub q .

Więc: nie jest tak, że p - i - nie jest tak, że q, i odwrotnie

Często popełniamy błąd utożsamiając negację alternatywy (1) z alternatywą negacji (2):

1. „Nieprawda, że Jan czyta gazetę lub pali papierosa”,

2. „Nieprawda, że Jan czyta gazetę, lub nieprawda, że Jan pali papierosa”.

Prawo negacji implikacji

T 6 Neg. Impl. ~(p ⊃ q) ⊃ (p ⊃ ~q)

Ponieważ: nie jest tak, że jeżeli p to q.

Więc: jeżeli p, to nie jest tak, że q

• „Jeżeli 1 listopada jest piątek, to 2 listopada jest niedziela” wynika „Jeżeli 1 listopada jest piątek, to 2 listopada nie jest niedziela”.

Prawo transpozycji (p ⊃ q) ≡ (~q ⊃ ~p)

T 7 Transp.

Transpozycją zdania warunkowego nazywamy takie zdanie warunkowe, które powstaje z poprzedniego przez przestawienie poprzednika z zastępnikiem oraz zanegowanie każdego z nich.

Ponieważ: jeżeli p, to q .

Więc: jeżeli nie jest tak, że q, to nie jest tak, że p, i odwrotnie.

PRAWA O BUDOWIE SYLOGICZNEJ

Sylogizm nazywamy wypowiedź o postaci zdania warunkowego (implikację materialną albo formalną) mającego w poprzedniku koniunkcję dwóch zdań (funkcji zdaniowych), w których powtarza się pewien składnik wspólny, następnik zaś jest zdaniem (funkcją zdaniową) zbudowanym ze składników nie powtarzających się w poprzedniku.

Prawo sylogizmu hipotetycznego [(p ⊃ q) ∙(q ⊃ r)] ⊃ (p ⊃ r)

T 8 Syl. hip.

Ponieważ: jeżeli p, to q,

i jeżeli q, to r,

Więc: jeżeli p, to r.

Za zmienne zdaniowe p,q,r, podstawiać można dowolne zdania, nawet nie powiązane treściowo: prawo to głosi, że jeżeli pierwsze z nich implikuje drugi, a drugi implikuje trzecie, to pierwsze implikuje trzecie.

Prawo modu ponendo ponens (tryb przez stwierdzenia stwierdzający):

T 9 MPP [(p ⊃ q) ∙p] ⊃ q

Ponieważ: jeżeli p, to q,

i p ,

Więc: q

• „Jan kowalski jest notariuszem, to ma wykształcenie prawnicze, a ponieważ stwierdziliśmy, że jest notariuszem, wnioskujemy dedukcyjnie, że ma wykształcenie prawnicze”

Prawo modus tollento tollens (tryb przez zaprzeczenie zaprzeczający):

T 10 MTT [(p ⊃ q) ∙ ~p] ⊃ ~q

Ponieważ: jeżeli p, to q,

i nie jest tak, że q,

Więc: nie jest tak, że p.

• „Obawiam się, że pada deszcz. Wiadomo, że jeśli pada deszcz, to jest mokro na dworze, a wyglądając na ulicę spostrzegam, że chodniki są mokre. Wnioskuję więc, że nie pada deszcz.

• „Jeśli Piotr zasztyletował kogoś, to był na miejscu zbrodni. Okazuje się, że nie było go na miejscu zbrodni. Wnioskuje więc, że na pewno nie on zasztyletował.

Prawo modus tollendo ponens [(p v q) ∙ ~p] ⊃ q

T 11 MTP

Ponieważ: p lub q,

i nie jest tak, że p,

Więc: q

• Jeśli wiadomo, że dane przestępstwo popełnił Jan lub popełnił Piotr, i stwierdzono, że Jan go nie popełnił, to musimy z takich przesłanek wyciągnąć wniosek, iż dane przestępstwo popełnił Piotr.

Prawo modus ponendo tollens [(p / q) ∙ p] ⊃ ~q

T 12 MPT

Ponieważ: bądź p, bądź q

i p ,

Więc: nie jest tak, że q

• Jeśli wiadomo, że z pewnej porcji gliny bądź zostanie zrobiony wazonik, bądź zostanie zrobiona figurka, i wiadomo, że zostanie zrobiony wazonik, to niewątpliwie nie zostanie zrobiona figurka z tej porcji gliny.

Prawo eksportacji i importacji: [(p∙q) ⊃ r] ≡ [p ⊃ ∙(q ⊃ r)]

T 13 Pr. eksp. imp.

1) eksportacja

Ponieważ: jeżeli zarazem p i q, to r,

Więc: jeżeli p, to jeśli q, to r.

2) importacja

Ponieważ: jeżeli p, to jeśli q, to r ,

Więc: jeżeli zarazem p i q, to r.

Dylemat - wzór wnioskowania z „z założenia dwójkowego”.

Prawo dylematu konstrukcyjnego: [(p ⊃ r) ∙ (q ⊃ r) ∙ (p v q)] ⊃ r

T 14 DK

Ponieważ {jeżeli p, to r

Zarazem: {i jeżeli q, to r

{i p lub q

Więc: r

• „Jeżeli Jan nadawał list na poczcie, to był na poczcie, i jeśli Jan wysyłał przekaz to był na poczcie, a że nadawał list polecony lub wysyłał przekaz, więc był na poczcie.

Prawo dylematu konstrukcyjnego złożonego [(p ⊃ q) ∙ (r ⊃ s) ∙ (p v r)] ⊃ (p v s)

T 15 DKZ

Ponieważ {jeżeli p, to q

Zarazem: {i jeżeli r, to s

{i p lub r

Więc: q lub s

• „Jeżeli pójdę do kawiarni, to wypiję kawę, jeżeli pójdę do restauracji, to wypiję herbatę, a wiadomo, że pójdę do kawiarni lub pójdę do restauracji - wnioskować więc można, że wypiję kawę lub herbatę.

Prawo konwersji :

Konwersja jakiegoś zdania subsumpcyjnego nazywamy zdanie powstałe zeń w ten sposób, że termin, który poprzednio był orzecznikiem, stawiamy na miejscu podmiotu - i odwrotnie.

1) Konwersja prosta

SeP ≡ PeS

SiP ≡ PiS

2) Konwersja ograniczona :

SaP
PiS

SoP NIE!!!!!

Prawo obwersji:

Obwersja jakiegoś zdania subsumpcyjnego nazywamy zdanie powstające zeń przez wpisanie na miejsce dotychczasowego orzecznika nazwy w stosunku do tego ostatniego negatywnej, przy jednoczesnej zmianie tzw. jakości zdania: z twierdzącego na odpowiednie przeczące - i odwrotnie; a więc zdania rodzaju a zmieniamy na zdania rodzaju e - i odwrotnie, natomiast zdania rodzaju i zmieniamy na zdania rodzaju o - oraz odwrotnie.

SaP ≡ S e nie-P

SeP ≡ S a nie-P

SiP ≡ S o nie-P

SoP ≡ S i nie-P

Prawo kontrapozycji:

Kontrapozycją jakiegoś zdania subsumpcyjnego nazywamy zdanie powstające zeń przez przestawienie i zanegowanie obu jego terminów.

S a P ≡ S e nie-P S o P ≡ S i nie-P

S e nie-P ≡ nie-P e S S i nie-P ≡ nie-P i S

Nie-P e S ≡ nie-P a nie-S nie-P i S ≡ nie-P o nie-S

1) kontrapozycja prosta:

SaP ≡ nie-P a nie-S

SoP ≡ nie-P i nie-S

2) Kontrapozycja ograniczona:

SeP
nie-P o nie-S

Kwadrat logiczny - jest graficznym przedstawieniem zależności logicznych pomiędzy zdaniami subsumpcyjnymi o tym samym podmiocie i orzeczniku.

SaP - Każde S są P; Nie istnieją S, które nie są P;

SeP - Żadne S nie są P; Nie istnieją S, które są P;

SiP - Niektóre S są P; Istnieją S, które Są P;

SoP - Niektóre S nie są P; Istnieją S, które nie są P;

S a P ≡ ~S o P S e P ≡ ~S i P

S i P ≡ ~S e P S o P ≡ ~S a P

S a P / S e P S i P v S o P

S a P ⊃ S i P S e P ⊃ S o P

SaP przeciwne SeP

wynikanie wynikanie

SiP SoP

sprzeczność

sprzeczność

podprzeciwne

---