1994 / 95 |
LABORATORIUM FIZYCZNE |
|||
Ćwiczenie nr 21 |
Charakterystyki prądowo - napięciowe oporników nieliniowych |
|||
ELEKTRONIKA |
|
|||
Wykonane dnia 16.12.94 |
|
Data |
Ocena |
Podpis |
|
T |
|
|
|
|
S |
|
|
|
1. Zasada pomiaru
Oporniki, których rezystancja nie podlega prawu Ohma, lecz zmienia się wraz ze zmianą pewnego parametru, nazywamy opornikami nieliniowymi. Takimi opornikami są termistor i warystor.
Termistor jest elementem półprzewodnikowym, którego opór w dużo większym stop-
niu niż w metalach zależy od temperatury i którego współczynnik temperaturowy oporu może
być dodatni - opór rośnie ze wzrostem temperatury (termistory PTC) lub ujemny (NTC).
Opór elektryczny termistora w zależności od temperatury wyraża sie wzorem:
![]()
(1)
E - szerokość przerwy energetycznej półprzewodnika
kB- stała Boltzmana
A- stała materiałowa o wymiarze oporu
Wprowadzając oznaczenie ![]()
oraz uwzględniając moc wydzieloną na termisto- rze (P), temperaturę otoczenia (T0) i zdolność odprowadzania ciepła (C), otrzymamy:
![]()
(2)
Spadek napięcia na termistorze wynosi:
![]()
(3)
Warystor to opornik półprzewodnikowy, którego opór zależy od przyłożonego pola elektrycznego, czyli również napięcia. Charakterystyka prądowo-napięciowa warystora wyraża
się wzorem:
![]()
(4)
- współczynnik nieliniowości, względny przyrost oporu
C - stała, spadek napięcia na warystorze przy prądzie 1A
2. Układy pomiarowe
układ do badania charakterystyki termistora NTC:
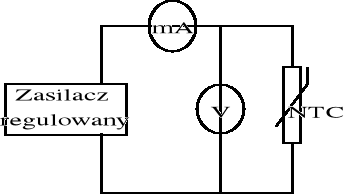
układ do badania charakterystyki warystora VDR:
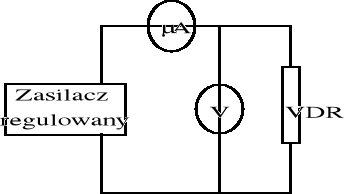
3. Ocena dokładności pojedynczych pomiarów
1. pomiar charakterystyki termistora:
amperomierz:
klasa: 0,5
zakresy: 75, 150, 300 mA
woltomierz: METEX
zakres: 200V
błąd: 0,3% + 1 cyfra
2. pomiar charkterystyki warystora:
amperomierz: METEX
zakresy: 200A, 2mA
błąd: 0,5% + 1 cyfra
woltomierz:
klasa: 0,5
zakresy: 50, 200 V
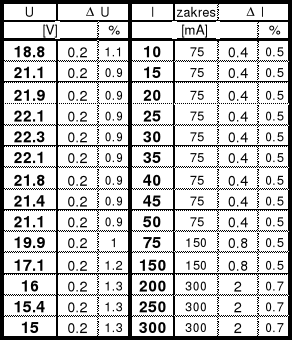
4a. Tabela wyników
termistor:
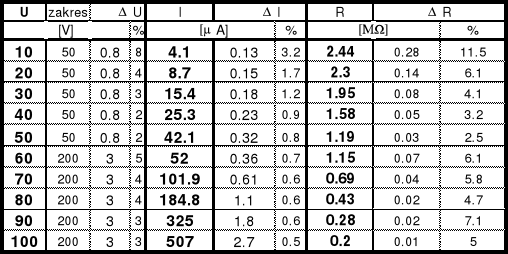
warystor:
4b. Wykresy
termistor:
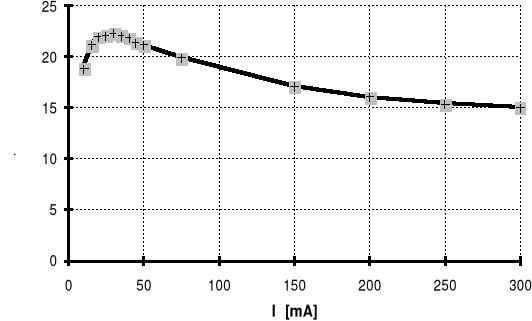
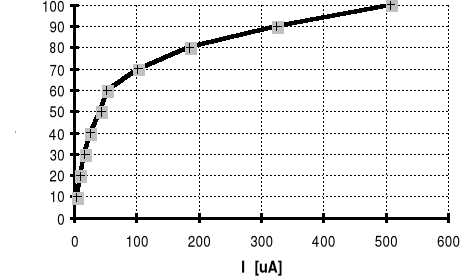
warystor:

5. Przykładowe obliczenia
termistor - pomiar 4:
U= 22,1 V
U= 0,3%*22,1+0,1= 0,1663 0,2V
I= 25 mA
I= 0,5*75/100= 0,375 0,4 mA
warystor - pomiar 4:
U= 40 V
U= 0,5*40/100= 0,8V
I= 25,3 A
I= 0,5%*25,3+0,1= 0,2265 0,23 A
R= 40/25,3= 1,5831027667 1,58 M
R= 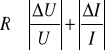
= 1,58*(0,8/40+0,23/25,3)=
=1,58*(0,02+0,00909)=1,58*0,02909=
=0,045963636 0,05 M = 50 k
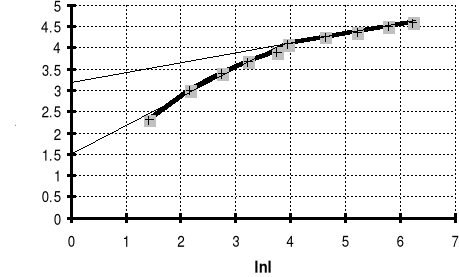
Logarytmując wzór (4) otrzymamy:
lnU= lnI + lnC (5)
według którego z wykresu lnU= f(lnI) łatwo wyznaczamy współczynnik nieliniowości , który jest współczynnikiem kierunkowym prostej, oraz współczynnik C - który jesy wartością
lnU w punkcie lnI=0.
Jak widać z wykresu lnU= f(lnI) dla warystora, przez uzyskane punkty pomiarowe moż-
na poprowadzić dwie proste, dla których współczynniki C i wynoszą odpowiednio:
niższa: lnC1 1,5 C1= 4,5
0,7
wyższa: lnC2 3,2 C2= 24,5
0,225
6. Dyskusja błędów
Błędy przyrządów pomiarowych podałem w punkcie 3., pragnę jedynie dodać, że zastosowany sprzęt miał wystarczającą dokładność jak na skromne studenckie potrzeby. Błędy poszczególnych pomiarów są przyzwoite. Jedynie na wykresie lnU= f(lnI) wystąpił dziwny błąd, wskutek którego zamiast prostej otrzymaliśmy linię łamaną. Na współczynniki odczytane z tego wykresu należy nałożyć oczywiście błąd wynikający z subiektywnej interpretacji wykresu. Z dwu poprowadzonych prostych, prawdopodobnie bardziej poprawna jest ta przebiegająca wyżej.
Duża różnica w wartościach C jest spowodowana stosunkowo dużą jak dla funkcji e rozbieżnoś-
cią logarytmów naturalnych C1 i C2.
7. Wnioski
Doświadczenie przebiegało bez większych niespodzianek. Wyniki natomiast potwier-
dzają nieliniowy charakter rezystancji termistora i warystora i są zgodne z oczekiwaniami.
Wyszukiwarka
Podobne podstrony:
5 1? 21 94
D19220541 Rozporządzenie Rady Ministrów z dnia 21 lipca 1922 r o rozciągnięciu na obszar Ziemi Wile
D19210072 Ustawa z dnia 21 stycznia 1921 r zmieniająca art 8 ustawy z dnia 18 lipca 1919 r w brzmie
W 21 Alkohole
1
1
21 02 2014 Wykład 1 Sala
X~1
SEM18 ~1
21 Fundamnety przyklady z praktyki
BO I WYKLAD 01 3 2011 02 21
1
w 1 komunikacja 21 11 09 nst
21 25
21 23
więcej podobnych podstron