1. 
   
   III zasada Newtona. Siły kontaktowe

4. Podstawowe wielkości kinematyczne ruchu obrotowego

Musi w pierwszym kroku wypracować ujęcie matematyczne dla ruchu obrotowego. Dla ruchu obrotowego wielkością analogiczną do przesunięcia jest przesunięcie kątowe θ. Kąt θ określa położenie punktu względem układu odniesienia. Dla ruchu po okręgu, z definicji miary łukowej kąta θ = S/R. (w radianach).

Kątową analogią prędkości v = dx/dt jest prędkość kątowa ω.

Dla ruchu po okręgu v = ω R.

W przypadku ruchu jednostajnego po okręgu ω jest nazywane częstością kątową i jest związana z częstotliwością f relacją ω = 2πf.

Podobnie jak przyspieszenie liniowe a = dv/dt zostało zdefiniowane przyspieszenie kątowe α.

Dla ruchu po okręgu związek pomiędzy a i α jest analogiczny do związku pomiędzy v i ω tzn. a = αR. Możemy teraz np. podać opis ruchu obrotowego ze stałym przyspieszeniem α poprzez analogię do ruchu postępowego jednostajnie zmiennego.

Ruch post.	Ruch obrotowy
a = const v = v0 + at s = s0 + v0t + (1/2)at^2	α = const ω = ω0 + αt θ =θ0 + ω0t + (1/2)αt^2

Kierunek i zwrot wektorów prędkości kątowej  i przyspieszenia kątowego  w ruchu obrotowym przyspieszonym (1) i opóźnionym (2) są pokazane na rysunku poniżej.

6. Druga zasada Newtona. Siła tarcia. Spółczyn. tarcia.

II zasada dynamiki: Jeżeli na ciało działa niezrównoważona siła, to ciało porusza się ruchem zmiennym. Przyspieszenie w tym ruchu jest wprost proporcjonalne do działającej siły, a odwrotnie proporcjonalne do masy ciała. (wzór a=F/M | a). Jeżeli na ciało działa kilka sił, wówczas siła F jest ich wypadkową.

Tarcie: Siły kontaktowe, są prostopadłe do powierzchni. Istnieje jednak składowa siły kontaktowej leżąca w płaszczyźnie powierzchni. Jeżeli ciało pchniemy wzdłuż stołu to po pewnym czasie ciało to zatrzyma się. Z drugiej zasady dynamiki wiemy, że jeżeli ciało porusza się z przyspieszeniem to musi działać siła. Taką siłę nazywamy siłą tarcia. Rozważmy np. klocek, do którego przykładamy "małą" siłę F tak, że klocek nie porusza się. Oznacza to, że sile F przeciwstawia się siła tarcia T. Mamy więc: T = -F. Zwiększamy stopniowo siłę F aż klocek zaczyna się poruszać. Im gładsza powierzchnia tym szybciej to nastąpi. Oznacza to, że siła tarcia zmienia się od wartości zero do pewnej wartości krytycznej w miarę wzrostu siły F. Oznaczmy tę krytyczną siłę T_s (s-statyczna). To jest maksymalna siła tarcia statycznego. T_s (dla pary powierzchni suchych) spełnia dwa prawa empiryczne:

Jest w przybliżeniu niezależna od powierzchni zetknięcia,

Jest proporcjonalna do siły prostopadłej z jaką jedna powierzchnia naciska na drugą.

Stosunek siły T_s do nacisku F_N nazywamy współczynnikiem tarcia statycznego μ_s

Uwaga: Mówimy tylko o wartościach tych sił bo są one do siebie prostopadłe. Jeżeli F jest większe od T_s to klocek poruszy się, ale będzie istniała siła tarcia T_k (k - kinetyczna) przeciwstawiająca się ruchowi. Siła T_k spełnia trzy prawa empiryczne: Jest w przybliżeniu niezależna od powierzchni zetknięcia, Jest proporcjonalna do siły prostopadłej z jaką jedna powierzchnia naciska na drugą, Nie zależy od prędkości względnej poruszania się powierzchni. Istnieje odpowiedni współczynnik tarcia kinetycznego μ_k

(5.2)

11. Wyprowadzenie wzoru na okres wahadła prostego

Wahadło proste jest to wyidealizowane ciało o masie punktowej, zawieszone na cienkiej, nieważkiej, nierozciągliwej nici. Kiedy ciało wytrącimy z równowagi to zaczyna się ono wahać w płaszczyźnie poziomej pod wpływem siły ciężkości. Jest to ruch okresowy. Znajdźmy okres tego ruchu.

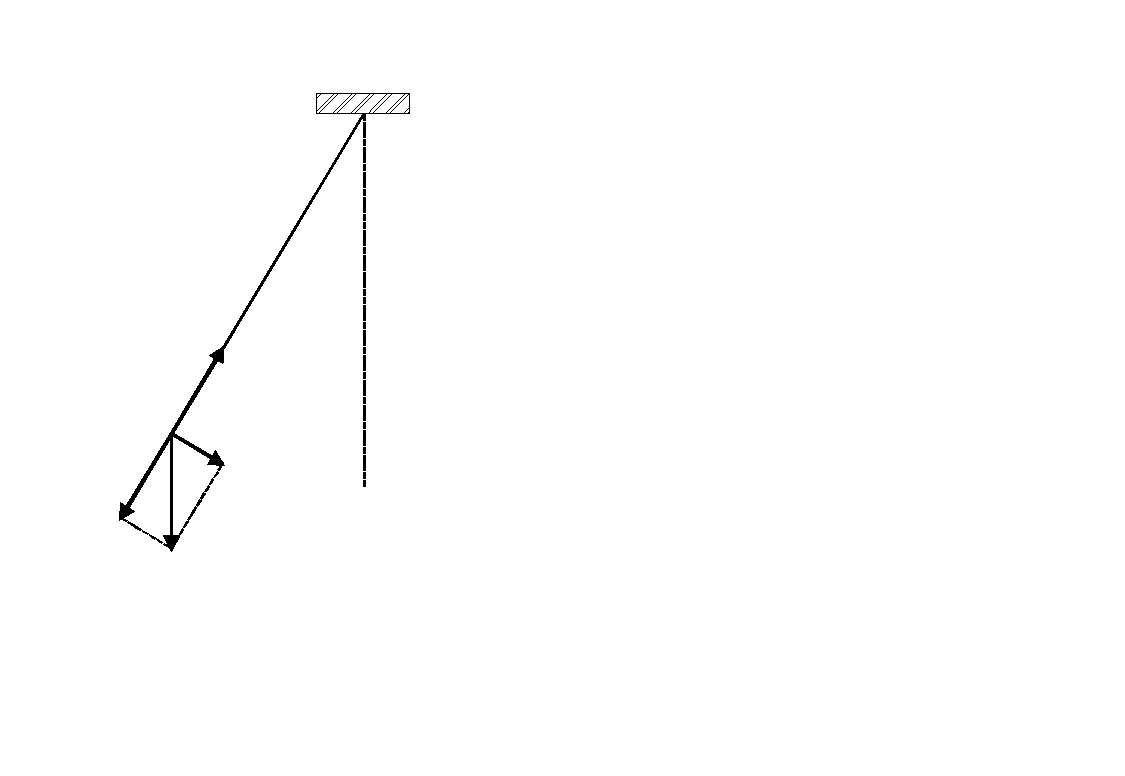
Rysunek przedstawia wahadło o długości l i masie m, odchylone o kąt θ od pionu. Na masę m działają: siła przyciągania grawitacyjnego mg i naprężenia nici N. Siłę mg rozkładamy na składową radialną i styczną. Składowa styczna jest siłą przywracającą równowagę układu i sprowadza masę m do położenia równowagi. Siła ta wynosi: F = mgsinθ. Przemieszczenie wzdłuż łuku (z miary łukowej kąta) wynosi x = lθ. Przyjmując zatem, że sinθ ≅ θ otrzymujemy:
.

F jest więc proporcjonalna do przemieszczenia (ze znakiem "-"). Jest to kryterium ruchu harmonicznego. Stała mg/l określa stałą k w równaniu F = - kx. Przy małej amplitudzie okres wahadła prostego wynosi więc:

.

Zauważmy, że okres wahadła nie zależy od amplitudy i od masy wahadła.

23. Wyprowadzenie wzoru na okres wahadła fizycznego

Dowolne ciało sztywne zawieszone tak, że może się wahać wokół pewnej osi przechodzącej przez to ciało nazywamy wahadłem fizycznym. P jest punktem zawieszenia ciała a punkt S, znajdujący się w odległości l od punkt P, jest środkiem masy. Moment siły τ działający na ciało wynosi: τ = - mglsinθ. Korzystając ze związku: τ = Iα =I(d²θ /dt²) otrzymujemy:

Dla małych wychyleń, dla których sinθ ≅ θ dostajemy równanie

To równanie ma tę samą postać co równanie dla ruchu harmonicznego więc

lub

Jako przypadek szczególny rozpatrzmy masę punktową zawieszoną na nici o długości l. Wówczas I = ml² i otrzymujemy znany wzór dla wahadła prostego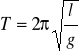

Wahadło fizyczne stosuje się do precyzyjnych pomiarów przyspieszenia g.

16. Praca wyk. przez stała silę. Praca wyk. przez zmn. siłę.

W najprostszym przypadku, siła F jest stała, a punkt porusza się w kierunku działania siły. Wtedy W = F·s = Fs cosα . Wzór Fs cosα określa jedynie pracę wykonaną przy przemieszczaniu punktu przez jedną siłę. Pracę wykonaną przez inne należy obliczyć oddzielnie i potem je zsumować. Zwróćmy uwagę, że gdy α = 0 otrzymujemy pierwszy wzór Fs. Gdy α = 90° to z równania wynika, że W = 0.

Praca wykonana przez siłę zmienną

Rozważmy teraz siłę będącą funkcją położenia F(x), której kierunek jest zgodny z osią x. Szukamy pracy jaką wykona ta siła przy przesuwaniu ciała od położenia x₁ do położenia x₂. Zaczynamy od przybliżenia. Dzielimy całkowite przemieszczenie na n jednakowych odcinków Δx. Wewnątrz takiego przedziału przyjmujemy, że siła jest stała i możemy teraz policzyć pracę na tym odcinku Δx: ΔW_i = F_iΔx, gdzie F_i jest wartością siły na tym odcinku. Następnie możemy zsumować prace na kolejnych odcinkach i otrzymać pracę całkowitą.

Żeby poprawić to przybliżenie dzielimy przedział (x₁, x₂) na więcej (mniejszych) odcinków Δx.I teraz znowu powtarzamy procedurę sumowania. Przybliżenie jest lepsze bo siła ma prawie stałą wartość wewnątrz "małych" przedziałów Δx.Widać, że rozwiązaniem problemu jest przejście Δx → 0. Stosujemy tę samą procedurę obliczając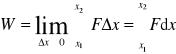

To jest definicja całki. Liczbowo odpowiada to liczeniu pola powierzchni pod krzywą (w zadanym przedziale - granicach). Odpowiada to też z definicji liczeniu wartości średniej co zgadza się z intuicyjnym podejściem: W = F_średnia(x₂ - x₁)

Siła wywierana przez sprężynę jest siłą przywracającą równowagę i wynosi F = -k x.

Aby rozciągnąć sprężynę musimy przyłożyć siłę równą co do wartości lecz przeciwnie skierowaną. Tak więc F = k x. Teraz obliczmy pracę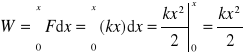

25. Prawo Pascala i prawo Archimedesa

Na rysunku widzimy ciecz w naczyniu zamkniętym tłokiem, na który możemy działać ciśnieniem zewnętrznym p₀.

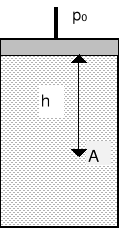
W każdym punkcie A znajdującym się na głębokości h od górnej powierzchni cieczy, ciśnienie jest dane wyrażeniem p = p₀ + ρgh. Możemy powiększyć ciśnienie zewnętrzne o wartość Δp₀. Ponieważ ciecze są nieściśliwe więc gęstość pozost. praktycznie bez zmian i dlatego ciś. teraz wynosi: p = p₀ +Δp₀+ ρgh

Jest to prawo Pascala: ciśnienie wywierane na zamknięty płyn jest przekazywane niezmienione na każdą część płynu oraz na ścianki naczynia. Prawo to jest konsekwencją praw mechaniki płynów podobnie jak prawo Archimedesa. Kiedy ciało jest zanurzone w całości lub częściowo w spoczywającym płynie to płyn ten wywiera ciśnienie na każdą, będącą z nim w kontakcie, część powierzchni ciała. Wypadkowa siła jest skierowana ku górze i zwie się siłą wyporu.

Ponieważ ciśnienie wywierane na ciało nie zależy od materiału, z którego zrobiono ciało więc zastąpmy w naszym rozumowaniu rozpatrywane ciało przez ten sam płyn co płyn otoczenia. Na ten płyn będzie działało to samo ciśnienie co na ciało, które zastąpił. Poza tym płyn będzie nieruchomy. Stąd działająca nań siła będzie równa ciężarowi płynu i skierowana ku górze tak, żeby ten ciężar zrównoważyć. Otrzymujemy prawo Archimedesa: ciało w całości lub częściowo zanurzone w płynie jest wypierane ku górze siłą równą ciężarowi wypartego przez to ciało płynu. Tak więc

F_wyporu = m_{wypartego płynu} g = ρVg (

gdzie ρ jest gęstością płynu, a V objętością części zanurzonej ciała.

3. Ruch ciała rzuconego pod kątem do horyzontu: opis analityczny i graficzny

Rzut ukośny: to ruch ze stałym przyspieszeniem g skierowanym w dół. Przyjmijmy, że początek układu współrzędnych pokrywa się z punktem, z którego wylatuje ciało.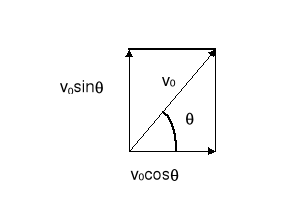

Prędkość w chwili początkowej t = 0 jest równa v₀ i tworzy kąt θ z dodatnim kierunkiem osi x. Składowe prędkości początkowej wynoszą odpowiednio:

v_x0 = v₀ cosθ i v_y0 = v₀ sinθ

Prędk. w kierunku x: v_x = v_x0 + a_xt. ponieważ a_x = 0 więc: v_x = v₀ cosθ, czyli w kierunku x ruch jest jednostajny. W kierunku y: v_y = v_y0 + a_yt, ponieważ: g_y = -g więc: v_y = v₀ sinθ - gt. Wartość wektora wypadkowego prędkości w dowolnej chwili wynosi:

Więc:

Teraz obliczamy położenie ciała: x = v_0xt. czyli: x = v₀ cosθ t, y = v_0yt+(1/2)a_yt^2, czyli: y = v₀ sinθ t - (1/2)gt². Długość wektora położenia r można teraz obliczyć dla dowolnej chwili t z zależności

22.Podst. wielkości dynamiczne i prawa ruchu obrotowego

Moment siły: W ruchu postępowym siłę wiążemy z liniowym przyspieszeniem ciała. Wielkością z którą będziemy wiązać przyspieszenie kątowe nie może być tylko siła. Dla ruchu obrotowego odpowiednikiem siły w ruchu postępowym jest moment siły (tzw. moment obrotowy) τ. Jeżeli siła F działa na cząstkę to moment siły jest definiowany jako:
, gdzie wektor r reprezentuje położenie cząstki względem wybranego inercjalnego układu odniesienia. Moment siły jest wielkością wektorową, której iloczyn wektorowy wynosi: τ = rFsinθ . Wielkość r nazywamy ramieniem siły (widać, że bierzemy albo r_⊥ albo F_⊥).

Moment pędu: Zdefiniujmy teraz wielkość, która w ruchu obrotowym odgrywa rolę analogiczną do pędu. Wielkość L będziemy nazywać momentem pędu i definiujemy ją:
, gdzie p jest pędem cząstki, a r reprezentuje położenie cząstki względem wybranego inercjalnego układu odniesienia. Wartość L wynosi rpsinθ i analogicznie do momentu siły wielkość rsinθ nazywamy ramieniem pędu.

Istnieje bezpośrednia zależność pomiędzy momentem siły i momentem pędu. Zacznijmy od znanej zależności, że siła F = dp/dt. Mnożąc wektorowo obie strony przez r otrzymujemy:
gdzie:
jest momentem siły τ więc:
. Teraz przechodzimy do równania na moment pędu L = r×p i różniczkujemy je obustronnie względem czasu, otrzymując:

ponieważ dr/dt = v więc:
. Wiemy, że
= 0, więc:
. Ostatecznie:

Widzimy, że wypadkowy moment siły działający na cząstkę jest równy prędkości zmian momentu pędu tej cząstki.

Zachowanie momentu pędu:
Zauważmy, że jeżeli na układ nie działa zewnętrzny moment siły (lub suma = 0) to moment pędu układu pozostaje stały.

17. Energia kinetyczna i twierdzenie o pracy i energii

Energia kinetyczna i twierdzenie o pracy i energii:

Rozważmy przypadek gdy ciało porusza się pod wpływem niezrównoważonej siły. Najprostszy przypadek to stała siła czyli ruch ze stałym przyspieszeniem. Zakładamy, że kierunek siły F i przyspieszenia a pokrywa się z kierunkiem osi x. Dla stałego przyspieszenia mamy:
oraz:

co w połączeniu daje:
. Wykonana praca jest równa:

Połowę iloczynu masy ciała i kwadratu prędkości nazywamy energią kinetyczną.

Praca wykonana przez wypadkową siłę F działającą na punkt materialny jest równa zmianie energii kinetycznej tego punktu.

W = E_k - E_k0

Twierdzenie o pracy i energii:

Gdy nie ma zmiany wartości prędkości to nie ma zmiany energii kinetycznej tzn. nie jest wykonywana praca (np. siła dośrodkowa). Z twierdzenia powyższego wynika, że jednostki pracy i energii są takie same.

Moc: Rozważmy czas w jakim wykonywana jest praca. Często interesuje nas szybkość wykonania pracy a nie jej wartość. To jest właśnie moc. Moc średnia: Pśrednia = W/t. Moc chwilowa: P = dW/dt. Oczywiście gdy moc jest stała w czasie to Pśrednia = P. Jednostką mocy jest wat. 1W = 1J/1s.

27. Opis przepływu płynów

Znane są dwa podejścia do opisu ruchu płynu. Pierwsze wymaga podzielenia płynu na nieskończenie małe cząstki i śledzenie tych elementów. Oznacza to, że dla każdej cząstki mamy współrzędne x, y, z i ich zależność od czasu. Drugie podejście: Zamiast opisywać historię każdej z cząstek określamy gęstość płynu i jego prędkość w każdym punkcie przestrzeni i w każdej chwili czasu. Czyli podajemy ρ(x,y,z,t) oraz v(x,y,z,t). Oznacza to, że koncentrujemy się na wybranym punkcie przestrzeni w pewnym czasie.

Na wstępie rozpatrzmy pewne ogólne właściwości charakteryzujące przepływ: Przepływ może być ustalony (laminarny) lub nieustalony, wirowy lub bezwirowy, ściśliwy lub nieściśliwy, lepki lub nielepki.

W przepływie ustalonym v jest stała w czasie w danym punkcie. Rozważmy punkt P wewnątrz płynu. Każda cząstka ma tam taką samą prędkość. To samo dla punktów Q i R. Jeżeli prześledzimy tor jednej cząstki to prześledziliśmy zarazem tor każdej cząstki przechodzącej przez P. Tor tej cząstki nazywamy linią prądu. Linia prądu jest równoległa do prędkości płynu. Żadne linie prądu nie mogą się przecinać bo istniała by niejednoznaczność w wyborze drogi przez cząstkę (a przepływ jest ustalony). Jeżeli wybierzemy pewną skończoną liczbę linii prądu to taką wiązkę nazywamy strugą prądu. Brzegi składają się z linii prądu więc płyn nie może przepływać przez brzegi strugi. Płyn wchodzący jednym końcem strugi musi opuścić ją drugim.

Równanie to nosi nazwę równania Bernoulliego dla przepływu ustalonego, nielepkiego i nieściśliwego. Jest to podstawowe równanie mechaniki płynów. Może być stosowane do wyznaczenia prędkości płynu na podstawie pomiarów ciśnienia. Można też w oparciu o nie wyznaczyć dynamiczną siłę nośną.

Dynamiczna siła nośna jest to siła wywołana ruchem tych ciał w płynie w odróżnieniu od statycznej siły nośnej, która jest siła wyporu działającą zgodnie z prawem Archimedesa.

5. I,II,III zasada Newtona: formuowanie i przykłady

Podstawowa teoria, która pozwala nam przewidywać ruch ciał, składa się z trzech równań, które nazywają się zasadami dynamiki Newtona.

Sformułowanie pierwszej zasady dynamiki Newtona

Ciało pozostaje w stanie spoczynku lub w stanie stałej prędkości (zerowe przyspieszenie) gdy jest pozostawione samo sobie (działająca na nie siła wypadkowa jest równa zero).

a = 0, gdy F_wypadkowa = 0

gdzie F_wypadkowa jest sumą wektorową wszystkich sił działających na ciało.

Uwaga: a = 0, oznacza, że nie zmienia się ani wartość ani kierunek tzn. ciało jest w spoczynku lub porusza się ze stałą co do wartości prędkością po linii prostej (stały kierunek).

Sformułowanie drugiej zasady dynamiki Newtona

Tempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało.

Zwróćmy uwagę, że w definicji F mówimy o pojedynczej sile, a tu mamy do czynienia z siłą wypadkową.

Sformułowanie trzeciej zasady dynamiki Newtona

Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na drugie

F_A→B = - F_B→A

Pierwsza zasada dynamiki stwierdza, że jeżeli na ciało nie działają siły zewnętrzne to istnieje taki układ odniesienia, w którym to ciało spoczywa lub porusza się ruchem jednostajnym prostoliniowym. Taki układ nazywamy układem inercjalnym. Ponieważ przyspieszenie ciała zależy od przyspieszenia układu odniesienia (obserwatora), w którym jest mierzone więc druga zasada dynamiki jest słuszna tylko, gdy obserwator znajduje się w układzie inercjalnym. Inaczej mówiąc, prawa strona równania F = ma zmieniałaby się w zależności od przyspieszenia obserwatora.

24. Moment bezwładności ciala sztywnego. Tw. Steinera

Większość mas w przyrodzie to nie cząstki tylko rozciągłe ciała stałe, które mogą wykonywać zarówno ruch postępowy jak i obrotowy. Przez ciała stałe, sztywne, rozumiemy ciała, w których odległość między dwoma wybranymi elementami pozostaje stała. Przeanalizujmy ruch takiej bryły obracającej się ze stałą prędkością kątowa ω wokół stałej osi w układzie środka masy. Zauważmy, że różne części ciała mają różną prędkość liniową v chociaż tą samą kątową ω. Dla potrzeb opisu ciało możemy podzielić na elementy o masie Δm_i odległe od osi obrotu o r_i. Wtedy prędkość takiego elementu wynosi v_i = r_iω. Wartość momentu pędu L tego ciała można obliczyć
. Wielkość w nawiasie nazywamy momentem bezwładności I, który definiujemy jako:
, a dla ciągłego rozkładu masy mamy:
. Zwróćmy uwagę, że I zależy od osi obrotu. Możemy teraz zapisać moment pędu: L = Iω , a ponieważ τ = dL/dt więc,
. Energia kinetyczna w układzie środka masy:

więc
. Zestawmy teraz obliczone wielkości z ich odpowiednikami dla ruchu postępowego.

Ruch postępowy	Ruch obrotowy
p = mv F = ma Ek = (1/2) mv^2	L= Iω τ = Iα Ek = (1/2)Iω^2

Teraz widzimy, że moment bezwładności I jest analogiczną wielkością do masy m w ruchu postępowym. Chociaż masa ciała nie zależy od jego położenia to moment bezwładności zależy od osi, wokół której obraca się ciało.

Często do obliczania momentu bezwładności wygodnie jest posłużyć się twierdzeniem Steinera. Podaje ono zależność pomiędzy momentem bezwładności I ciała względem danej osi, a momentem bezwładności I_śr.m. tego ciała względem osi przechodzącej przez jego środek masy i równoległej do danej: I = I_śr.m. + md² , gdzie m jest masą ciała, a d odległością pomiędzy osiami.

8. ciążenie powszechne. Doświadczenie Cawendisha

Prawo powszechnego ciążenia - Siła działająca między każdymi dwoma punktami materialnymi o masach m1 i m2 znajdującymi się w odległości r jest siłą przyciągającą, skierowaną wzdłuż prostej łączącej te punkty. Skoro istnieje siła przyciągania pomiędzy dowolnym ciałem i Ziemią, to musi istnieć siła między każdymi dwoma masami m1 i m2. Skoro siła jest proporcjonalna do masy ciała to musi być proporcjonalna do każdej z mas m1 i m2 oddzielnie czyli:F~m1m2

Gdyby ciało znalazło się w odległości takiej jak Księżyc to będzie ono miało takie samo przyspieszenie jak Księżyc bowiem natura siły grawitacyjnej pomiędzy Ziemią i Księżycem jest taka sama jak pomiędzy Ziemią i każdym ciałem.

Doświadczenie Cavendisha: Newton obliczył wartość stałej G na podstawie przyjętego założenia o średniej wartości gęstości Ziemi. W tym celu trzeba zmierzyć siłę oddziaływania dwóch mas m1 i m2 umieszczonych w odległości x.

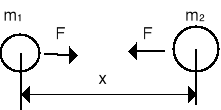
Wówczas siła:

F = Gm1m2/x2

Czyli: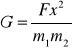

Zauważmy, że dla mas każda po 1 kg oddalonych od siebie o 10 cm siła F ma wartość F = 6.67·10-9 N tj. 109 razy mniej niż ciężar 1 kg i jest za mała by ją wykryć zwykłymi metodami.

Problem ten rozwiązał Henry Cavendish. Wykorzystał on fakt, że siła potrzebna do skręcenia długiego, cienkiego włókna kwarcowego o kilka stopni jest bardzo mała. Cavendish najpierw wykalibrował włókna, a następnie zawiesił na nich pręt z dwiema małymi kulkami ołowianymi na końcach (rysunek a). Następnie w pobliżu każdej z kulek umieścił większą kulę ołowianą i zmierzył precyzyjnie kąt o jaki obrócił się pręt (rysunek b). Pomiar wykonane metodą Cavendisha dają wartość G = 6.67·10-11 Nm2/kg2.

32. Transform. wzajemna E. kin i pot. w ruchu drającym

Energią potencjalna (nagromadzona) sprężyny:

Jeżeli masę przymocowaną do sprężyny pociągniemy na odległość x = A to energia układu jest równa (1/2)kA² (E_k = 0). Jeżeli teraz zwolnimy sprężynę, to przy założeniu, że nie ma tarcia ani sił oporu, zgodnie z zasadą zachowania energii w dowolnej chwili suma energii kinetycznej i potencjalnej równa się (1/2)kA²
stąd:
. Ponieważ k/m = ω² więc:
. Obliczmy teraz wartości średnie czasowe) energii potencjalnej i kinetycznej:
czyli:
. Natomiast:
, czyli:

Wartość średnia
jest taka sama jak
i wynosi 1/2. Oba wykresy są takie same (tylko przesunięte). Poza tym sin²ωt + cos²ωt = 1 i średnia każdego składnika jest taka sama. Widać, że

18. Praca i energia: zas. zach. energii mechanicznej

E_k + E_p. = const. W = ΔE_k = - ΔE_p

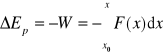
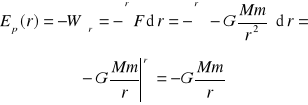
Gdy działają siły zachowawcze to

W = ΔE_k = E_kB - E_kA

oraz

W = -ΔE_p = - (E_pB - E_pA)

więc

- (E_pB - E_pA) = E_kB - E_kA

czyli

E_kA + E_pA = E_kB + E_pB

Równania to nazywa się zasadą zachowania energii mechanicznej.

Mówi ona, że dla ciała podlegającego działaniu siły zachowawczej, którego energia potencjalna jest równa E_p, suma energii kinetycznej i potencjalnej jest stała (o ile nie działają inne siły).

33. Opis analityczny rozchodzenia się fal. Prędkość fal

Jeżeli chcemy zmierzyć prędkość fali v to śledzimy jak przemieszcza się w czasie wybrana część fali czyli określona faza. Wiemy, że prędkość fali zależy od sprężystości ośrodka i jego bezwładności. Sprężystość dla sznura jest określona poprzez napinającą go siłę F. Natomiast bezwładność jest związana z masą sznura m oraz jego długością l. Spróbujemy teraz wyprowadzić wzór na zależność prędkości v fali od siły F i od μ = m/l tj. masy przypadającej na jednostkę długości sznura. W tym celu rozpatrzmy mały wycinek sznura o długości dx. Końce wycinka sznura tworzą z osią x małe kąty ₁ i ₂. Dla małych kątów  ≅ sin ≅ dy/dx. Wypadkowa pionowa siła tj. siła wychylająca sznur w kierunku y wynosi:
. Zgodnie z zasadą dynamiki siła wypadkowa jest równa iloczynowi masy wycinka dm = μ⋅dx i jego przyspieszenia. Stąd:
, lub
(Uwaga: w równaniach piszemy pochodne cząstkowe oznaczane symbolem ∂y bo wychylenie y jest funkcją dwóch zmiennych y = f (x,t) i liczymy pochodne zarówno względem zmiennej x jak i zmiennej t).Uwzględniają, że  = ∂y/∂x otrzymujemy
. Jest to równanie falowe dla sznura (struny). Podstawmy teraz do tego równania odpowiednie pochodne funkcji
:
oraz:
. W wyniku podstawienia otrzymujemy:
,skąd możemy obliczyć prędkość fali:
. Zwróćmy uwagę, że sinusoidalna fala może być przenoszona wzdłuż struny z prędkością niezależną od amplitudy i częstotliwości. Jeżeli teraz przepiszemy równanie struny w postaci:
, to otrzymamy równanie falowe, które stosuje się do wszystkich rodzajów rozchodzących się fal, takich jak fale dźwiękowe czy elektromagnetyczne.

7. III zasada Newtona. Siły kontaktowe

III zasada dynamiki: Jeżeli ciało A działa na ciało B, to ciało B oddziałuje na ciało A siłą o takim samym kierunku i wartości lecz przeciwnym zwrocie. Trzecia zasada dynamiki zwana jest także zasadą akcji i reakcji. Przejawy trzeciej zasady Newtona spotykamy na każdym kroku. Słońce przyciąga Ziemię, a Ziemia przyciąga Słońce. Podobnie oddziałują między sobą Ziemia i Księżyc oraz wszystkie planety i inne obiekty Układu Słonecznego. Wzajemność oddziaływań obserwujemy oczywiście powszechnie w naszym otoczeniu jak i w mikroświecie.

Gdy dwa ciała są dociskane do siebie to występują między nimi siły kontaktowe. Źródłem tych sił jest odpychanie pomiędzy atomami. Przy dostatecznie małej odległości występuje przekrywanie chmur elektronowych i ich odpychanie rosnące wraz z malejącą odległością. To jest siła elektromagnetyczna i może być bardzo duża w porównanie z siłami grawitacyjnymi.

Jeżeli siła ciężkości pcha blok w dół siłą Fg to powstaje druga siła - siła kontaktowa F1. Siła wypadkowa Fwyp = 0. We wszystkich przypadkach stosowania drugiej zasady dynamiki Newtona jest bardzo istotne, żeby obliczyć siłę wypadkową.

Rozważmy dwa klocki m1 i m2 na gładkiej powierzchni. Do klocka m1 przyłożono siłę F. Czy siła F jest przenoszona poprzez klocek 1 na klocek 2? Gdyby tak było to zgodnie z trzecią zasadą dynamiki Newtona klocek 2 działałby na klocek 1 siłą równą i przeciwnie skierowaną. Wtedy Fwyp równałaby się zero!!!!, czyli, że nie można by było poruszyć ciała 1 bez względu na to jak duża jest siła F.

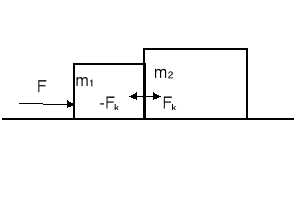
Zasada Newtona nie mówi, że siła F jest przenoszona przez klocek 1 na klocek 2; powinno się przyjąć siłę kontaktową Fk o dowolnej wartości. Ogólnie: powinno się stosować drugą zasadę dynamiki oddzielnie do każdego ciała.

Dla klocka 1 otrzymujemy wtedy F - Fk = m1a

Dla klocka 2 Fk = m2a

Stąd przyspieszenie a = F/(m1 + m2)

Zauważmy, że ten wynik można otrzymać gdy traktujemy te dwa klocki jak jedną masę m = m1 + m2.

20. Ruch postępowo-obrotowy ciała sztywnego

Rozpatrywaliśmy ruch obrotowy ciała względem osi nieruchomych. Jednakże gdy ciało się toczy to wykonuje zarówno ruch postępowy, jak i obrotowy. Dlatego też toczenie możemy traktować jako złożenie ruchu postępowego i obrotowego tak jak pokazano to na rysunku poniżej dla toczącego się walca.

W ruchu postępowym, rysunek (a), wszystkie punkty poruszają się z takimi samymi prędkościami, natomiast w ruchu obrotowym, rysunek (b), przeciwległe punkty poruszają się z przeciwnymi prędkościami, a środek jest nieruchomy. Na rysunku (c) pokazano wynik złożenia (sumowania) odpowiednich wektorów z rysunków (a) i (b).

Zwróćmy uwagę, że podstawa walca (punkt P styczności z podłożem na rysunku poniżej) w każdej chwili spoczywa (v = 0). Natomiast prędkość liniowa każdego innego punktu jest w każdej chwili prostopadła do linii łączącej ten punkt z podstawą P i proporcjonalna do odległości tego punktu od P. Oznacza to, że walec obraca się wokół punktu P. Oznacza to, że możemy toczenie opisywać również jako "czysty" ruch obrotowy ale względem osi przechodzącej przez punkt P styczności z powierzchnią, po której toczy się ciało.

9. Pole grawitacyjne wewnątrz kuli

Rozpatrzmy teraz pole czaszy kulistej o masie m i promieniu R. Dla r > R pole jest równe Gm/r² tj. tak jakby cała masa była skupiona w środku kuli.

Rozważmy przyczynki od dwóch leżących naprzeciwko siebie powierzchni A₁ i A₂ w punkcie P wewnątrz czaszy. Fragment A₁ czaszy jest źródłem siły F₁ ~ A₁/(r₁)² ciągnącej w lewo. Powierzchnia A₂ jest źródłem siły ciągnącej w prawo F₂ ~ A₂/(r₂)² .
Mamy więc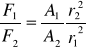
Z rozważań geometrycznych widać, że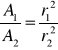
(pola powierzchni stożków ~ do kwadratu wymiarów liniowych)

Po podstawieniu do pierwszego równania otrzymujemy
Tak więc wkłady wnoszone przez A₁ i A₂ znoszą się. Można w ten sposób podzielić całą czaszę i uzyskać siłę wypadkową równą zero. Tak więc wewnątrz czaszy pole grawitacyjne jest równe zeru. Pole wewnątrz czaszy mającej skorupę dowolnej grubości też jest zero bo możemy podzielić tę skorupę na szereg cienkich warstw koncentrycznych.

Na rysunku poniżej przedstawiono pełną kulę o promieniu R i masie M.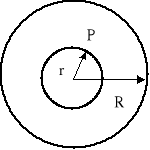
W punkcie P pole pochodzące od zewnętrznej warstwy jest zerem. Pole pochodzi więc tylko od kuli o promieniu r czyli

a = Gm/r² lub a = GρV/r²

Dla kuli V = 4πr³/3. Gęstość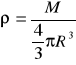
więc pole w punkcie P wynosi
Widzimy, że pole zmienia się liniowo z r.

30. Wpływ tłumienia na charakterystyki ruchu drgającego

W przypadku drgań mechanicznych siłą hamującą ruch cząstki jest siła oporu F_op ośrodka. Siła oporu ma zwrot przeciwny do prędkości i w najprostszej postaci jest wprost proporcjonalna do prędkości F_op ≈ v czyli F_op = γ dx/dt . Gdy działa tylko siła tłumienia to
lub
Jeżeli wprowadzimy zmienną (o wymiarze czasu) τ = M/γ to otrzymamy równanie dv/dt = - (1/τ)v co można przepisać w postaci dv/v = - dt/τ Całkujemy to równanie obustronnie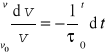
Skąd otrzymujemy lnv - lnv₀ = - (t/τ) Lub ln(v/v₀) = - (t/τ) a po przekształceniu

Prędkość maleje wykładniczo z czasem czyli prędkość jest tłumiona ze stałą czasową τ . Jeżeli włączymy siłę hamującą do oscylatora to wówczas równanie ruchu przyjmie postać

Wprowadzając τ = M/γ oraz oznaczając częstość drgań nietłumionych ω₀² = (k/M) otrzymujemy
Szukamy rozwiązania w postaci drgań okresowo zmiennych tłumionych np.

Rozwiązanie zawiera czynnik oscylacyjny (cost) i tłumiący (exp(-t)) i jest pokazane na rysunku poniżej. Współczynnik β = 1/2τ określający wielkość tłumienia nazywamy współczynnikiem tłumienia.

W wyniku rozwiązania dostajemy warunek na częstość drgań tłumionych

Opór zmniejsza więc (oprócz amplitudy) również i częstość

Funkcja (13.16) jest rozwiązaniem równania opisującego ruch harmoniczny tłumiony przy warunku (13.17). Widzimy, że opór zmniejsza zarówno amplitudę jak i częstość drgań, czyli powoduje spowolnienie ruchu. Wielkość tłumienia określa współczynnik tłumienia  (lub stała czasowa ). Wykres ruchu harmonicznego tłumionego w zależności od czasu jest pokazany na rysunku

15. Zas. zach. pędu. Środ. masy układu. Ruch środka masy

Środek masy. Dotychczas przedmioty traktowaliśmy jak punkty materialne, tzn. cząsteczki bezwymiarowe obdarzone masą co wystarczało w przypadku ruchu postępowego bo ruch jednego punktu odzwierciedlał ruch całego ciała.

W ogólnym przypadku ruch układu cząsteczek może być bardzo skomplikowany np. ciało może wirować lub drgać. W trakcie ruchu cząsteczki mogą zmieniać swoje wzajemne położenie. Zauważmy, że istnieje w tym układzie jeden punkt, który porusza się po linii prostej ze stałą prędkością. Żaden inny punkt nie porusza się w ten sposób. Ten punkt to środek masy. Zacznijmy od przypomnienia pojęcia średniej ważonej.

Ruch środka masy.

Ma_śrm = F_zew

Z równania wynika, że środek masy układu punktów materialnych porusza się w taki sposób, jakby cała masa układu była skupiona w środku masy i jakby wszystkie siły zewnętrzne nań działały.

To twierdzenie obowiązuje dla każdego układu punktów materialnych.

• Układ może być ciałem sztywnym (punkty mają stałe położenia względem siebie). Wtedy przy obliczeniach środka masy sumowanie zastępujemy całkowaniem.

• Układ może być zbiorem cząsteczek, w którym występują wszystkie rodzaje ruchu wewnętrznego.

Uwaga:

Gdy siłą zewnętrzną jest siła ciężkości to wtedy działa ona na środek ciężkości. W rozważanych przypadkach te dwa środki się pokrywają.

Pojęcie środka masy jest bardzo użyteczne np. do obliczania energii kinetycznej.

Zasada zachowania pędu

Przypuśćmy, że suma sił zewnętrznych działających na układ jest równa zeru. Wtedy na podstawie równania

Zasada zachowania pędu: Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru, całkowity wektor pędu układu pozostaje stały.

Rozważmy dwa ciała o masach mA i mB połączone nieważką sprężyną umieszczone na doskonale gładkim stole. Odciągamy od siebie te ciała na pewną odległość, a następnie puszczamy swobodnie.

Spróbujmy opisać ruch tych ciał. Najpierw ustalamy z czego składa się rozważany układ. Przyjmujemy, że tworzą go obie masy + sprężyna. Jeżeli tak to nie działa żadna siła zewnętrzna. Możemy teraz zastosować zasadę zachowania pędu. Przed zwolnieniem ciał pęd układu (w odniesieniu do stołu) był równy zeru. I taki pozostaje po ich zwolnieniu. Chociaż ciała poruszają się ich pęd może być równy zeru, ponieważ pęd będący wielkością wektorową jest sumą dodatniego pędu ciała A (porusza się w kierunku +x) i ujemnego pędu ciała B (porusza się w kierunku -x). Z zasady zachowania pędu

34. Interferencja fal. Fale stojące

Rozważmy dwie fale o równych częstotliwościach i amplitudach ale o fazach różniących się o ϕ. Równania tych fal są następujące: y₁ = Asin(kx - ωt - ϕ), y₂ = Asin(kx - ωt).

Znajdźmy teraz falę wypadkową jako sumę y = y₁ + y₂. Korzystając ze wzoru na sumę sinusów otrzymujemy: y = 2Acos(ϕ/2)sin(kx - ωt - ϕ/2), co jest równaniem fali sinusoidalnej o amplitudzie 2Acos(ϕ/2). Dla ϕ = 0 fale spotykają się zgodnie w fazie (wzmacniają), a dla ϕ = 180 wygaszają.

Fale stojące

Rozważmy teraz dwa ciągi falowe biegnące w przeciwnych kierunkach tzn: y1 = Asin(kx - ωt), y2 = Asin(kx + ωt), np. falę padającą i odbitą.

Falę wypadkową można zapisać jako: y = y1 + y2 = 2Asinkxcosωt . To jest równanie fali stojącej. Zauważmy, że cząstki drgają ruchem harmonicznym prostym. Cząstki mają tę samą częstość ale różną amplitudę zależną od położenia cząstki x. Punkty kx = π/2, 3π/2, 5π/2, itd. czyli x = λ/4, 3λ/4, 5λ/4 itd. mające maksymalną amplitudę nazywamy strzałkami a punkty kx = π, 2π, 3π itd. czyli x = λ/2, λ, 3λ/2 itd. mające zerową amplitudę nazywamy węzłami.

Zwróćmy uwagę na jeszcze jedną istotną różnicę. Energia nie jest przenoszona wzdłuż sznura bo nie może ona przepłynąć przez węzły, jest na stałe zmagazynowana w poszczególnych elementach sznura.

29. Wyprowadzenie wzoru na masę zredukowaną

Dwie masy, m₁ i m₂, są przyczepione do przeciwnych końców sprężyny. Jaki będzie okres drgań, gdy rozciągniemy sprężynę, a następnie zwolnimy obie masy jednocześnie? Stała sprężyny wynosi k.

Niech x₁ będzie przesunięciem masy m₁ od położenia równowagi, a x₂ odpowiednim przesunięciem masy m₂. Zauważmy, że środek masy musi pozostawać nieruchomy.

Zatem m₁x₁ = - m₂x₂, czyli

Zastosujmy teraz do wybranej masy np. m₂ równanie F_wypadkowa = ma. Siłą wypadkową, działającą na m₂ jest siła F = - k (x₂ - x₁) gdzie (x₂ - x₁) jest wypadkowym rozciągnięciem sprężyny.

Podstawiamy teraz
zamiast x₁ i otrzymujemy

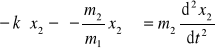
Czyli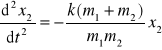
Więc

gdzie μ = m₁m₂/(m₁ + m₂) jest z definicji masą zredukowaną. To jest równanie jakie już rozwiązywaliśmy, w którym zamiast x jest x₂ a zamiast m jest μ.

Tak więc
czyli

Zwróćmy uwagę, że okres drgań harmonicznych T jest niezależny od amplitudy drgań A (o ile jest spełnione prawo Hooke'a). Tę właściwość drgań harmonicznych prostych zauważył Galileusz i wykorzystał ją do skonstruowania zegara wahadłowego.

31. Opis analityczny drgań wymusz. Zjawisko rezonansu

Jeżeli oprócz tarcia istnieje siła zewnętrzna F(t) (która ma za zadanie podtrzymywać gasnące drgania) przyłożona do oscylatora to równanie ruchu ma postać:
, albo po podstawieniu: τ = M/γ oraz ω02 = k/M. Otrzymujemy:
. W tym wzorze ω0 jest częstością własną układu, gdy nie działa siła zewnętrzna i nie ma tarcia.

Gdy układ jest zasilany częstością ω różną od ω₀ wówczas drgania będą odbywały się z częstością siły zewnętrznej a nie z częstością własną. Siłę taką nazywamy siłą wymuszającą. Załóżmy, że siła wymuszająca ma postać:
, gdzie α₀ = F₀/M.

Mamy teraz w równaniu dwie wielkości okresowo zmienne położenie x oraz siłę wymuszającą F (…) Równanie to może być tylko spełnione gdy czynniki przy sinωt będą sobie równe, a czynnik przy cosωt będzie równy zeru. Ten ostatni warunek można zapisać jako:
. Z tego warunku znam już ϕ. Teraz możemy wyznaczyć amplitudę:
, gdzie już podstawiono za cosϕ i sinϕ. Otrzymujemy rozwiązanie:

Rezonans. Zauważmy, że gdy siła wymuszająca działa na ciało z pewną charakterystyczną częstotliwością _r:
, to amplituda drgań osiąga wartość maksymalną. Zjawisko to nazywamy rezonansem. Maksymalna amplituda wynosi:
. Widać, że im mniejsze tłumienie (większe τ) tym większa amplituda A. Jeżeli tłumienie jest słabe (ω₀τ >> 1) to wówczas maksymalna amplituda odpowiada częstości drgań własnych ω_r = ω₀. Jednocześnie, ten warunek odpowiada przesunięciu fazowemu ϕ = π/2 pomiędzy siłą a wychyleniem. Siła nie jest zgodna w fazie z wychyleniem. Zauważmy jednak, że moc pochłaniana przez oscylator zasilany siłą wymuszającą F zależy od prędkości: P = Fv. Trzeba więc, żeby to prędkość (a nie wychylenie) była zgodna w fazie z siłą, a to oznacza, że siła musi wyprzedzać wychylenie o π/2. Gdy x = 0 to v = v_max i wtedy siła też ma być maksymalna. W punktach zwrotnych, gdzie prędkość zmienia swój kierunek, siła też musi zmienić swój kierunek.

13. Siła Coriolisa

Oprócz wyżej opisanych - czyli siły odśrodkowej, i sił występujących podczas hamowania i ruszania pojazdu, występują pewne bardziej skomplikowane rodzaje sił bezwładności. Najbardziej znaną jest siła Coriolisa.Siła Coriolisa pojawia się wtedy, gdy w obracającym się układzie nieinercjalnym ciało porusza się ruchem jednostajnym (względem tego układu, a najczęściej również względem układu inercjalnego). 
Opis siły Coriolisa jest bardziej skomplikowany od przykładów przedstawionych wyżej. Aby choć częściowo zrozumieć na czym polega ta siła, powinniśmy wyobrazić sobie, co się dzieje np. z obiektem poruszającym się od równika Ziemi w kierunku bieguna. Ponieważ w okolicach równika prędkość (liniowa, czyli w m/s) ruchu wirowego jest większa niż w pobliżu bieguna, to ciało poruszające się do bieguna północnego będzie miało "nadmiar" prędkości wynikającej z ruchu wirowego. I dlatego będzie ono zbaczało w kierunku zgodnym z kierunkiem obrotu Ziemi. Odwrotna sytuacja występuje, gdy ciało zbliża się od bieguna do równika - wtedy "brakuje mu" jakby prędkości adekwatnej do ruchu wirowego na danej szerokości geograficznej.Siła Coriolisa powoduje, że rzeki płynące na północ mają tendencje do podmywania przeciwnych brzegów, niż te płynące na południe.Oczywiście siła bezwładności może mieć swoje bardziej skomplikowane wydania - wszystko zależy od rodzaju ruchu ciała i ruchu układu odniesienia

Siła Coriolisa - siła ta jest nieco podobna do siły odśrodkowej i pojawia się, gdy opisujemy ruch ciała z poziomu obracającego się układu odniesienia

36. Opis analityczny zjawiska Dopplera

Austriak, Christian Doppler w pracy z 1842 r zwrócił uwagę, że barwa świecącego ciała (częstotliwość) musi się zmieniać z powodu ruchu względnego obserwatora lub źródła. Zjawisko Dopplera występuje dla wszystkich fal. Obecnie rozważymy je dla fal dźwiękowych. Zajmiemy się przypadkiem ruchu źródła i obserwatora wzdłuż łączącej ich prostej.

Źródło dźwięku spoczywa, a obserwator porusza się w kierunku źródła z prędkością vo. Nieruchomy obserwator odbierał by vt/λ fal w czasie t. Teraz odbiera jeszcze dodatkowo vot/λ fal. Częstość słyszana przez obserwatora

Ostatecznie

Studiując pozostałe przypadki otrzymujemy ogólną zależność

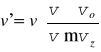
gdzie v' - częstość odbierana przez obserwatora, v - częstość źródła, v - prędkość fali, vo - prędkość obserwatora, vz - prędkość źródła.

Znaki "górne" w liczniku i mianowniku odpowiadają zbliżaniu się, a znaki dolne oddalaniu się obserwatora i źródła.

14. Definicja masz w fizyce. Sily bezwladnosci

Definicja o charakterze operacyjnym (recepta na postępowanie). Nieznaną masę m porównujemy ze wzorcem masy 1 kg. Umieszczamy pomiędzy nimi sprężynę i zwalniamy ją. Masy, które początkowo spoczywały polecą w przeciwnych kierunkach z prędkościami v₀ i v.

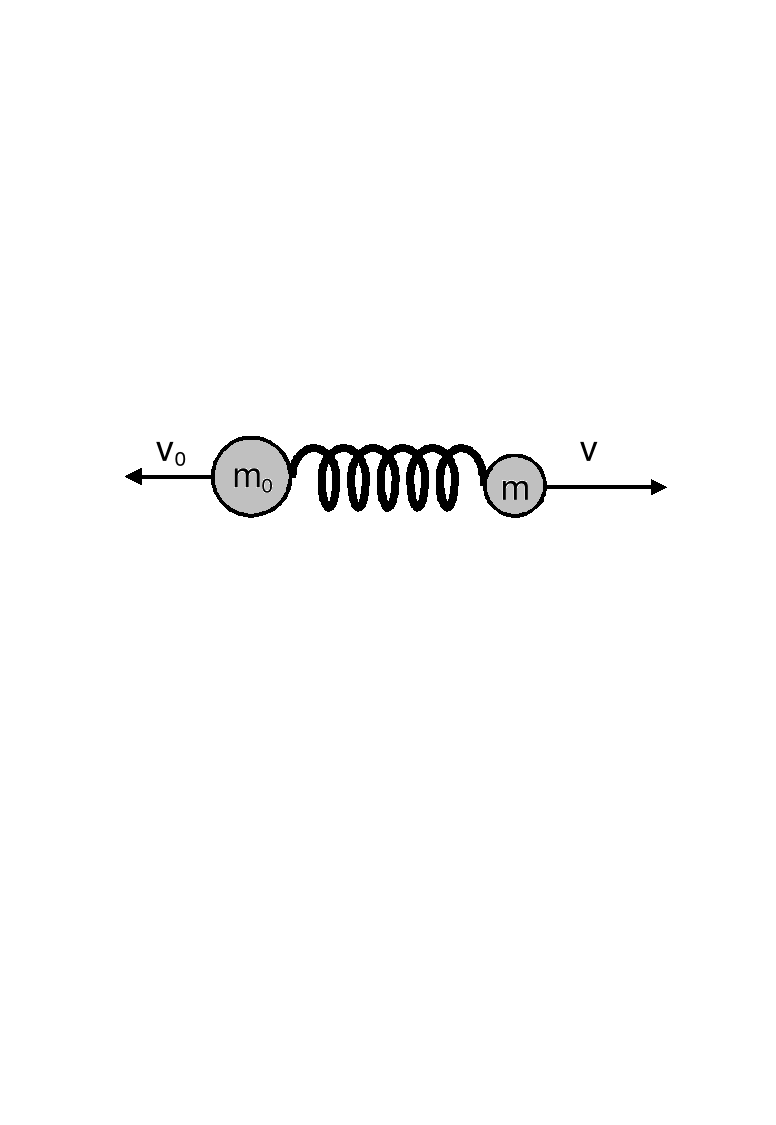
Nieznaną masę m definiujemy jako

Uwzględnienie sił bezwładności jest konieczne jeżeli chcemy stosować zasady dynamiki w układach nieinercjalnych.W takim układzie uwzględniamy, że na każde ciało działa siła wprost proporcjonalna do masy tego ciała, do przyspieszenia układu a i jest skierowana przeciwnie do a.

28. Prawo Hooke'a. Ruch harm. Gł. char. ruchu drgając.

Działającą na ciało siłę, która jest proporcjonalna do przesunięcia ciała od początku układu i która jest skierowana ku początkowi układu, nazywamy siłą harmoniczną lub siłą sprężystości. Jeżeli obierzemy oś x wzdłuż przesunięcia, to siła harmoniczna jest wyrażona równaniem F = - kx gdzie x jest przesunięciem od położenia równowagi. To równanie opisuje siłę wywieraną przez rozciągniętą sprężynę o ile tylko sprężyna nie została rozciągnięta poza granicę sprężystości. To jest prawo Hooke'a.

Jeżeli sprężyna zostanie rozciągnięta tak aby masa m (zaczepiona do sprężyny) znalazła się w położeniu x = A, a następnie w chwili t = 0 została zwolniona, to położenie masy w funkcji czasu będzie dane równaniem

x = Acosωt

Sprawdźmy czy to jest dobry opis ruchu. Dla t = 0, x = A tzn. opis zgadza się z założeniami. Z drugiej zasady dynamiki Newtona wynika, że

- kx = ma czyli - kx = m(dv/dt)

Wreszcie - kx = m(d²x/dt²) Równanie takie nazywa się równaniem różniczkowym drugiego rzędu. Staramy się "odgadnąć" rozwiązanie i następnie sprawdzić nasze przypuszczenia. Zwróćmy uwagę, że rozwiązaniem jest funkcja x(t), która ma tę właściwość, że jej druga pochodna jest równa funkcji ale ze znakiem "-". Zgadujemy, że może to być funkcja x = Acosωt i sprawdzamy dx/dt = v = - Aωsinωt . d²x/dt² = a = - Aω²cosωt Podstawiamy ten wynik (- kAcosωt) = m(- Aω²cosωt) i otrzymujemy ω² = k/m

Widzimy, że x = Acosωt jest rozwiązaniem równania ale tylko gdy
.

Zwróćmy uwagę, że funkcja x = Asinωt jest również rozwiązaniem równania ale nie spełnia warunku początkowego bo gdy t = 0 to x = 0 (zamiast x = A).

Najogólniejszym rozwiązaniem jest

x = Asin(ωt + ϕ)

gdzie ϕ jest dowolną stałą fazową. Stałe A i ϕ są określone przez warunki początkowe.

Wartości maksymalne (amplitudy) odpowiednich wielkości wynoszą:

• dla wychylenia A

• dla prędkości ωA (występuje gdy x = 0)

• dla przyspieszenia ω²A (występuje gdy x = A)

10. Prawa Keplera. Wyznaczanie masy planet

I prawo: każda planeta krąży po orbicie eliptycznej a Słońce znajduje się w jednym z ognisk elipsy.

II prawo: Promień wodzący poprowadzony ze środka Słońca do środka planety zakreśla równe pola powierzchni w równych odstępach czasu.

III prawo: Sześciany wielkich pół osi orbit jakichkolwiek dwóch planet mają się tak do siebie jak kwadraty ich okresów obiegu. 

Dla orbit kołowych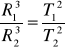

Newton rozwijając swoją teorię potrafił dowieść, że tylko wtedy, gdy siła jest odwrotnie proporcjonalna do kwadratu odległości, orbita dowolnej planety jest elipsą ze Słońcem w jednym z ognisk oraz, że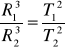
. Newton wyprowadził prawa Keplera z zasad dynamiki. Przykładowo wyprowadźmy III prawo Keplera dla planet poruszających się po orbitach kołowych.

Korzystając z otrzymanego uprzednio wzoru na masę Słońca otrzymamy dla pierwszej planety:

a dla drugiej

Porównując otrzymamy

Drugie prawo Keplera wynika z zasady zachowania pędu (dowód można pominąć).

19. Zderzenia sprężyste: definicja i opis analityczny

Jedyne prawdziwe zderzenia sprężyste (chociaż nie zawsze) to zderzenia między atomami, jądrami i cząsteczkami elementarnymi. Zderzenia między ciałami są zawsze w pewnym stopniu niesprężyste chociaż czasami możemy je traktować w przybliżeniu jako sprężyste. Kiedy dwa ciała po zderzeniu łączą się mówimy, że zderzenie jest całkowicie niesprężyste. Rozpatrzmy teraz zderzenie sprężyste w przestrzeni jednowymiarowej. Wyobraźmy sobie dwie gładkie nie wirujące kule, poruszające się wzdłuż linii łączącej ich środki. Masy kul m₁ i m₂, prędkości przed zderzeniem v₁ i v₂ a po zderzeniu u₁ i u₂ tak jak na rysunku poniżej.

Z zasady zachowania pędu otrzymujemy

m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂

Ponieważ zderzenie jest sprężyste to energia kinetyczna jest zachowana (zgodnie z definicją). Otrzymujemy więc

Przepisujemy równanie (10.5) w postaci

m₁(v₁ - u₁) = m₂(u₂ - v₁)

a równanie (10.6) w postaci

Dzieląc równanie (10.8) przez równanie (10.7) otrzymamy w wyniku (przy założeniu v₁ ≠ u₁ i v₂ ≠ u₂)

v₁ + u₁ = v₂ + u₂

a po uporządkowaniu

v₁ - v₂ = u₂ - u₁

Równanie to mówi nam, że w opisanym zderzeniu względna prędkość zbliżania się cząstek przed zderzeniem jest równa względnej prędkości ich oddalania się po zderzeniu.

Mamy do dyspozycji trzy równania (10.7), (10.8) i (10.9), a chcemy znaleźć u₁ i u₂. Wystarczą więc dowolne dwa. Biorąc dwa liniowe równania (10.7) i (10.9) obliczmy

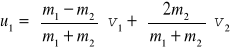
oraz

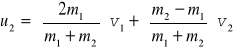
Przy zderzeniach niesprężystych energia kinetyczna nie jest zachowana.

35. Interferencja fal

Rozważmy dwie fale o równych częstotliwościach i amplitudach ale o fazach różniących się o ϕ. Równania tych fal są następujące: y₁ = Asin(kx - ωt - ϕ), y₂ = Asin(kx - ωt). Znajdźmy teraz falę wypadkową (zasada superpozycji) jako sumę y = y₁ + y₂. Korzystając ze wzoru na sumę sinusów otrzymujemy: y = 2Acos(ϕ/2)sin(kx - ωt - ϕ/2) , co jest równaniem fali sinusoidalnej o amplitudzie 2Acos(ϕ/2). Dla ϕ = 0 fale spotykają się zgodnie w fazie (wzmacniają), a dla ϕ = 180 wygaszają.

Dudnienia - modulacja amplitudy

Mówiliśmy już o superpozycji fal, interferencji w przestrzeni (dodawanie fal o tej samej częstości). Rozpatrzmy teraz przypadek interferencji w czasie. Pojawia się ona gdy przez dany punkt w przestrzeni przebiegają w tym samym kierunku fale o trochę różnych częstotliwościach. Wychylenie wywołane przez jedną falę ma postać: y₁ = Acos2πv₁t, y₂ = Acos2πv₂t, więc: y = y₁ + y₂ = A(cos2πv₁t + cos2πv₂t). Ze wzoru na sumę cosinusów:
. Drgania wypadkowe można więc uważać za drgania o częstości: v_srednie = (v₁ + v₂)/2, która jest średnią dwóch fal, i o amplitudzie (wyrażenie w nawiasie kwadratowym) zmieniającej się w czasie z częstością : v_amp = (v₁ - v₂)/2. Jeżeli częstotliwości v₁ i v₂ są bliskie siebie to amplituda zmienia się powoli. Mówimy, że mamy do czynienia z modulacją amplitudy AM (stosowana np. w odbiornikach radiowych). Dla fal dźwiękowych AM przejawia się jako zmiana głośności nazywana dudnieniami.

1.

2.

3. Ruch ciała rzuconego pod kątem

4. Podstawowe wielkości kinematyczne ruchu obrotowego

5. I,II,III zasada Newtona

6. II zasada Newtona. Tarcie

7. III zasada Newtona. Siły kontaktowe

8. Ciężar powszechny. Cowendish

9. Pole grawitacyjne wewnątrz kuli

10. Prawa Keplera. Masa planet

11. Wahadło proste

12.

13. Siła Coriolisa

14. Def. masy. Siły bezwładności

15. Zasada zachowania pędu. Masa układu

16. Praca wykonana przez siłę stałą/zmienną

17. Energia kinetyczna, Tw. O pracy i energii

18. Praca i energia: zasada zachowania energii mechanicznej

19. Zderzenia sprężyste: def. i opis analityczny

20. Ruch postępowo obrotowy ciała sztywnego

21.

22. Podstawowe wielkości dynamiczne i prawa ruchu obrotowego

23. Wahadło fizyczne

24. Moment bezwładności. Tw. Steinera

25. Prawo Pascala i Archimedesa

26. Zmiany ciśnienia wewnątrz nieruchomego płynu

27. Opis przepływu płynów

28. Prawo Hooke'a. Ruch harmoniczny i drgający

29. Wyprowadzenie wzoru na masę zred.

30. Wpływ tłumienia na charakterystyki ruchu drgającego

31. Opis analityczny drgań wymuszonych. Rezonans

32. Transform. Wzajemna energii kin. i pot. W ruchu drgającym

33. Opis analityczny rozchodzenia się fal. Prędkość fal

34. Interferencja fal. Fale stojące

35. Interferencja fal

36. Opis analityczny zjawiska Dopplera.

---