Wydział EAIiE |
Nazwiska :
|
Rok |
Grupa |
Zespół |
||
Pracownia fizyczna I |
Temat : Moduł Younga |
Nr Ćwiczenia 11 |
||||
Data Wykonania
|
Data Oddania
|
Zwrot do poprawki |
Data Oddania |
Data Zaliczenia
|
Ocena |
|
Cel ćwiczenia:
Celem ćwiczenia jest sprawdzenie prawa Hooke'a oraz wyznaczenie modułu Younga za pomocą pomiarów dokonanych przy wydłużaniu się metalowych prętów pod wpływem obciążenia.
Wstęp teoretyczny:
Rozpatrując teorię oddziaływań i odkształceń możemy podzielić ciała na mniej podatne na odkształcenia (ciała stałe, np. stal, drewno) i bardziej podatne (ciecze, a szczególnie gazy). Wpływ na takie a nie inne zachowanie danego ciała pod wpływem działającej nań siły zależy w dużej mierze od charakteru jego wiązań międzycząsteczkowych. Ciała, w których oddziaływania międzycząsteczkowe są bardzo silne ulegają mniejszemu odkształceniu nawet pod działaniem większej siły.
Ciała możemy również podzielić ze względu na sposób „reagowania” na działające nań siły. Ciała, które po zaniku działania siły powracają do swojego pierwotnego kształtu nazywamy sprężystymi. Jeżeli po usunięciu działającej siły odkształcenie ciała pozostaje to takie ciało nazywamy niesprężystym.
Odkształcenia możemy podzielić również na:
odkształcenia jednostronne - siły działają na dwie przeciwległe ścianki ciała prostopadle do nich co powoduje zmianę jego wymiarów wzdłuż prostej równoległej do wektorów tych sił. Skutkiem takiego odkształcenia jest zmiana długości ciała ΔL (wydłużenie lub, gdy ΔL<0 - skrócenie ciała).
odkształcenie wszechstronne - siły działają na każdy element ciała prostopadle do niego co skutkuje zmianą objętości danego ciała ΔV.
Mówiąc o sile działającej na dany element ciała (jego powierzchnię) lepiej jest stosować pojęcie naprężenia:
![]()
![]()
- naprężenie [![]()
], ![]()
- siła oddziaływania [N], S - powierzchnia [m2]
Naprężeniem P nazywamy więc wektor, którego wartość równa jest stosunkowi długości wektora siły i powierzchni na jaką działa ta siła i o zwrocie i kierunku takim samym jak wektor siły. Jeżeli zdefiniujemy również wydłużenie względne:
![]()
ε - wydłużenie względne [ - ], ΔL - zmiana długości [m], L - długość pierwotna
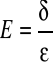
to wyrażenie: nazywamy prawem Hooke'a, gdzie E to tzw. Moduł Younga - wielkość
charakterystyczna dla danego ciała i opisująca w pewien sposób jego właściwości mechaniczne. Znając moduł Younga dla np. stali oraz znając parametry badanego ciała (np. długość i średnicę drutu stalowego) to możemy z pewnym przybliżeniem przewidzieć zmiany jakim ulegnie dane ciało pod wpływem działających nań sił.
Przebieg pomiarów:
Pomiarów dokonujemy badając wydłużenie trzech drutów o różnych długościach, średnicach i właściwościach ( druty: stalowy, miedziany i mosiężny ). Pomiarów długości drutów dokonujemy za pomocą przymiaru liniowego a średnicę mierzymy śrubą mikrometryczną. Ponieważ średnica drutu nie jest jednakowa na całej długości dokonujemy pomiaru w 10 różnych miejscach i obliczamy średnią. Pomiarów wydłużenia dokonujemy na specjalnej wadze połączonej z czujnikiem wydłużenia. Ważne jest aby przy nieobciążonym drucie czujnik wskazywał zero i aby po usunięciu jakiegokolwiek wcześniej zadanego obciążenia wskazówka czujnika powróciła na swoje miejsce.
Wyniki pomiarów:
Drut mosiężny:
L = 1066 mm ± 1 mm (Δ = ± 1mm - błąd wynikający z dokładności przymiaru)
Pomiar |
d [mm] |
Δd [mm] |
1 |
0,74 |
-0,031 |
2 |
0,74 |
-0,031 |
3 |
0,77 |
-0,001 |
4 |
0,77 |
-0,001 |
5 |
0,77 |
-0,001 |
6 |
0,79 |
0,019 |
7 |
0,78 |
0,019 |
8 |
0,78 |
0,009 |
9 |
0,78 |
0,009 |
10 |
0,78 |
0,009 |
wart. śr. |
dśr=0,771 |
Δdśr=0,006 |
Pomiaru średnicy dokonano śrubą mikrometryczną (Δ = ± 1mm )
dśr = ![]()
mm
Δd = 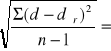
0,02 mm - błąd pojedynczego pomiaru.
Δdśr = 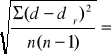
0,006 mm - odchylenie standardowe (błąd) średniej pomiarów.
Obciążenie [kg] |
Wydłużenie drutu przy |
|
|
Zwiększaniu masy obc. [mm] |
Zmniejszaniu masy obc. [mm] |
1 |
0,30 ± 0,01 |
0,36 ± 0,01 |
2 |
0,56 ± 0,01 |
0,64 ± 0,01 |
3 |
0,82 ± 0,01 |
0,90 ± 0,01 |
4 |
1,07 ± 0,01 |
1,14 ± 0,01 |
5 |
1,30 ± 0,01 |
1,40 ± 0,01 |
6 |
1,55 ± 0,01 |
1,62 ± 0,01 |
7 |
1,79 ± 0,01 |
1,79 ± 0,01 |
Średnica Dśr [mm] |
pole przekroju S [mm2] |
Obciążenie M [kg] |
Naprężenie δ [N/mm2] |
Wydłużenie ΔL [mm] |
wydł. wzg. ε=ΔL/L [-] |
Moduł Younga E [N/mm2] |
0,771 ±0,006 |
0,466 ± 0,004 |
1 |
21,42 |
0,30 |
0,00028 |
76099,28 |
|
|
2 |
42,83 |
0,56 |
0,00053 |
81534,95 |
|
|
3 |
64,25 |
0,82 |
0,00077 |
83523,61 |
|
|
4 |
85,67 |
1,07 |
0,00100 |
85344,99 |
|
|
5 |
107,08 |
1,30 |
0,00122 |
87806,87 |
|
|
6 |
128,50 |
1,55 |
0,00145 |
88373,36 |
|
|
7 |
149,91 |
1,79 |
0,00168 |
89278,49 |
Przykładowe obliczenia ( dla obciążenia M = 4 kg ) :
dśr = (0,771 ± 0,006) mm
S = 0,25πdśr2 = 0,466 mm2 ± 0,004 mm2
![]()
ΔS = ![]()
= 0,25πdśrΔdśr = 0,004 mm2
![]()
![]()
![]()
![]()
![]()
Takie same obliczenia i rachunek błędów wykonywaliśmy dla przypadków z drutami miedzianym i stalowym.
Drut miedziany:
L = 1063 mm ± 1 mm (Δ = ± 1mm - błąd wynikający z dokładności przymiaru)
Pomiar |
d [mm] |
Δd [mm] |
1 |
0,81 |
0,001 |
2 |
0,81 |
0,001 |
3 |
0,81 |
0,001 |
4 |
0,81 |
0,001 |
5 |
0,81 |
0,001 |
6 |
0,81 |
0,001 |
7 |
0,81 |
0,001 |
8 |
0,81 |
0,001 |
9 |
0,80 |
-0,009 |
10 |
0,81 |
0,001 |
wart. śr. |
dśr=0,809 |
Δdśr=0,001 |
dśr = (0,809 ± 0,001) mm
Δdśr = 0,001 mm, Δd = 0,003 mm
Obciążenie [kg] |
Wydłużenie drutu przy |
|
|
Zwiększaniu masy obc. [mm] |
Zmniejszaniu masy obc. [mm] |
1 |
0,25 ± 0,01 |
0,37 ± 0,01 |
2 |
0,51 ± 0,01 |
0,60 ± 0,01 |
3 |
0,72 ± 0,01 |
0,80 ± 0,01 |
4 |
0,90 ± 0,01 |
1,00 ± 0,01 |
5 |
1,13 ± 0,01 |
1,19 ± 0,01 |
6 |
1,30 ± 0,01 |
1,37 ± 0,01 |
7 |
1,51 ± 0,01 |
1,51 ± 0,01 |
średnica d [mm] |
Pole przekroju S [mm2] |
obciążenie M [kg] |
naprężenie δ [N/mm2] |
Wydłużenie ΔL [mm] |
wydł. wzg. ΔL/L [-] |
moduł Younga E [N/mm2] |
0,809 ± 0,001 |
0,5137 ± 0,0006 |
1 |
19,43 |
0,25 |
0,00024 |
82606,5 |
|
|
2 |
38,86 |
0,51 |
0,00048 |
80986,77 |
|
|
3 |
58,28 |
0,72 |
0,00068 |
86048,44 |
|
|
4 |
77,71 |
0,90 |
0,00085 |
91785 |
|
|
5 |
97,14 |
1,13 |
0,00106 |
91378,87 |
|
|
6 |
116,57 |
1,30 |
0,00122 |
95315,19 |
|
|
7 |
135,99 |
1,51 |
0,00142 |
95736,01 |
Drut stalowy:
L = 1068 mm ± 1 mm (Δ = ± 1mm - błąd wynikający z dokładności przymiaru)
Pomiar |
d [mm] |
Δd [mm] |
1 |
1,01 |
0,002 |
2 |
1,01 |
0,002 |
3 |
1,01 |
0,002 |
4 |
1,01 |
0,002 |
5 |
1,01 |
0,002 |
6 |
1,01 |
0,002 |
7 |
1,01 |
0,002 |
8 |
1,01 |
0,002 |
9 |
1,00 |
-0,008 |
10 |
1,00 |
-0,008 |
wart. śr. |
dśr=1,008 |
Δdśr=0,001 |
dśr = (1,008 ± 0,001) mm
Δdśr = 0,001 mm, Δd = 0,004 mm
Obciążenie [kg] |
Wydłużenie drutu przy |
|
|
Zwiększaniu masy obc. [mm] |
Zmniejszaniu masy obc. [mm] |
1 |
0,11 ± 0,01 |
0,12 ± 0,01 |
2 |
0,21 ± 0,01 |
0,22 ± 0,01 |
3 |
0,30 ± 0,01 |
0,32 ± 0,01 |
4 |
0,38 ± 0,01 |
0,38 ± 0,01 |
5 |
0,45 ± 0,01 |
0,47 ± 0,01 |
6 |
0,54 ± 0,01 |
0,57 ± 0,01 |
7 |
0,62 ± 0,01 |
0,63 ± 0,01 |
8 |
0,63 ± 0,01 |
0,69 ± 0,01 |
9 |
0,76 ± 0,01 |
0,77 ± 0,01 |
10 |
0,84 ± 0,01 |
0,84 ± 0,01 |
Średnica d [mm] |
pole przekroju S [mm2] |
obciążenie M [kg] |
Naprężenie δ [N/mm2] |
Wydłużenie ΔL [mm] |
wydł. wzg. ΔL/L [-] |
moduł Younga E [N/mm2] |
1,008 ± 0,001 |
0,7976 ± 0,0008 |
1 |
12,51 |
0,11 |
0,00010 |
125100,0 |
|
|
2 |
25,03 |
0,21 |
0,00020 |
125150,0 |
|
|
3 |
37,54 |
0,3 |
0,00028 |
134071,4 |
|
|
4 |
50,05 |
0,38 |
0,00036 |
139027,8 |
|
|
5 |
62,56 |
0,45 |
0,00042 |
148952,4 |
|
|
6 |
75,08 |
0,54 |
0,00051 |
147215,7 |
|
|
7 |
87,59 |
0,62 |
0,00058 |
151017,2 |
|
|
8 |
100,10 |
0,63 |
0,00059 |
169661,0 |
|
|
9 |
112,61 |
0,76 |
0,00071 |
158605,6 |
|
|
10 |
125,13 |
0,84 |
0,00079 |
158392,4 |
Opracowanie wyników:
Wykresy ΔL(F) zostały sporządzone przy pomocy oprogramowania dostępnego na komputerach laboratorium fizycznego.
Dla drutu stalowego metodą najmniejszych kwadratów znaleźć wartość i odchylenie standardowe współczynnika nachylenia a=ΔL/ΔF:
![]()
⇒ ![]()
![]()
,
![]()
, ![]()
W = 383471,6 - 301300,3 = 82171,3
![]()
![]()
![]()
![]()
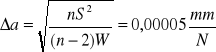
![]()
Obliczanie modułu Younga dla stali przy pomocy współczynnika nachylenia prostej regresji a=ΔL/ΔF dla stali. Obliczenie ΔE według prawa przenoszenia błędów biorąc pod uwagę błąd współczynnika a, przekroju S i długości L druta.
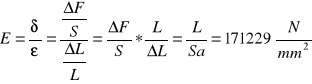
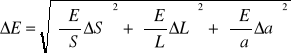
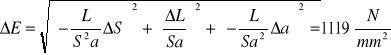
![]()
Tablicowa wartość ![]()
Wnioski:
Wartość wyliczonego modułu Younga dla stali odbiega (nawet po uwzględnieniu odchyłki standardowej pomiarów) od wartości tablicowej. Jest to zapewne związane z dużą ilością wielkości mierzonych potrzebnych do wyliczenia modułu. Im większa liczba wielkości mierzonych tym więcej jest błędów w mniejszym lub większym stopniu wpływających na ostateczny wynik. Mimo, że wyników nie sprawdziliśmy dla drutów miedzianego i mosiężnego to należy przewidywać podobne rezultaty.
![]()
![]()
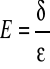
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Wyznaczanie modułu Younga metodą rozciągania, Wyznaczanie modu˙u Younga metod˙ rozci˙gania drutu i s
sprawdzanie prawa hooke a wyznaczanie modu u younga 1, fizyka 2 wykład i zagadnienia, sprawozda
WYZNACZANIE MODU U YOUNGA , laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
4.Wyznaczanie modu u Younga, Uczelnia, sem I, fiza, LABORATORIUM, Nowe laborki
spraw, LAB 2, Celem ˙wiczenia jest wyznaczenie modu˙u Younga dla materia˙u drutu poprzez pomiar jego
Wyznaczanie modu u Younga czysta
WYZNACZANIE MODUŁU YOUNGA PODCZAS PRÓBY 1, WYZNACZANIE MODU?U YOUNGA PODCZAS PR?BY
modu l Younga
wyznaczanie modulu younga. 3, SPRAWOZDANIE
wyznaczanie modułu younga2, BO˙ENA TANDEJKO
Wyznaczanie modułu Younga metodą ugięcia, 108@, nr ćw
Wyznaczanie modułu Younga metodą ugięcia, KONS108
wyznaczanie modulu younga, Laboratorium z Fizyki
modu- younga, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
Wyznaczanie modułu Younga metodą ugięcia, LAB 108, Nr ćw.
więcej podobnych podstron