1. Analiza portfolio i wycena aktywów

Podstawy teorii zarządzania portfelowego i metody efektywnego doboru aktywów oraz sposobu ich finansowania stworzył w swoich pracach H. Markowitz (1952, 1959), uważany współcześnie za ojca teorii portfelowej. Sam Markowitz uważa jednak, że tak naprawdę ojcem tej teorii jest znany angielski dramatopisarz W. Szekspir. Jako pierwszy oficjalnie nawiązał do zagadnień portfela w dziele zatytułowanym „Kupiec Wenecki”, w którym kupiec wypowiada się, że.

„My ventures are not in one bottom trusted,

Nor to one place; nor is my whole estate

Upon the fortune of this present year;

Therefore, my merchandise makes me not sad.

Act I, Scene 1”

z. angielskiego:

Moje przedsięwzięcia nie koncentrują się wokół jednego celu,

Ani nie znajdują się w jednym miejscu, nie stanowią również całego

mojego majątku powstałego dzięki sukcesom w bieżącym roku;

Dlatego też moje dobra nie powodują u mnie smutku.

Akt 1, Scena 1

Idee H. Markowitza zostały rozwinięte przez Williama Sharpe'a, który wprowadził 1963 roku model jednowskaźnikowy, upraszczający klasyczną teorię H. Markowitza. Wraz z pojawieniem się teorii portfelowej nastąpił zwrot w podejściu do inwestowania. Gwałtowny rozwój tej dziedziny nauki zaowocował licznymi modelami mającymi na celu ułatwienie podejmowania racjonalnych decyzji inwestycyjnych. Modele te przetrwały do dziś i są powszechnie stosowane.

2. Analiza ryzyka portfela

W procesie analizy istotne jest badanie zachowania się stopy zwrotu ze zbioru inwestycji (ang. rate of return of portfolio) w czasie, a nie tylko zachowanie się stóp zwrotu z poszczególnych inwestycji wchodzących w skład portfela inwestycji. Rozważa się dwa problemy:

• jakiej stopy zwrotu można oczekiwać ze zbioru dokonanych inwestycji (portfolio),

• jakie jest ryzyko związane z portfolio.

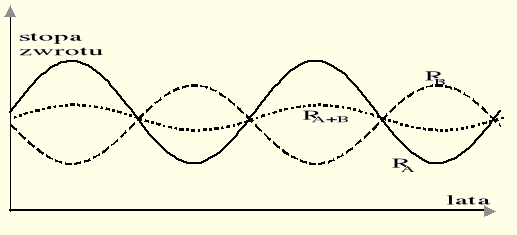
Rys. 7.24. Przeciwstawne zachowanie się stóp zwrotu (ujemnie skorelowanych) w czasie.

Odpowiednie zróżnicowanie, dopasowanie aktywów finansowych (typ, rodzaj i ilość) tworzących jeden zbiór, portfel (portfolio) inwestycji, nazywa się dywersyfikacją.

.

2. Oczekiwana stopa zwrotu z portfolio dwuskładnikowego

Załóżmy, że stopy zwrotu z inwestycji w papiery wartościowe R_i, i=1, 2,..., n, są zmiennymi losowymi o istniejących rozkładach prawdopodobieństwa.

Rozważmy kombinację liniową
, n papierów wartościowych, których wartości oczekiwane są odpowiednio
. Wówczas wartość oczekiwana kombinacji liniowej zmiennych losowych

.

Zgodnie z tym wyrażeniem, jeśli dwa lub więcej rodzajów papierów wartościowych tworzy zbiór (portfel, portfolio), który stanowi całość funduszu inwestora, to oczekiwany zwrot z portfolio
_p (ang. expected return of the portfolio) jest równy średniej ważonej oczekiwanych zwrotów z indywidualnych inwestycji
_r

,

gdzie n oznacza liczbę rodzajów papierów w portfelu, a W_i wartość udziału papieru i-tego w wartości całego portfela, przy czym
.

Dla portfela dwuskładnikowego, w którym udział zainwestowanego funduszu w papier wartościowy A wynosi W_A, a w papier B wynosi W_B, przy czym W_A+W_B=1, zachodzi

, (7.4)

a ryzyko portfela mierzone odchyleniem standardowym stóp zwrotu, wynosi

, (7.5)

gdzie

σ_AB, σ_p - odchylenie standardowe stóp zwrotu portfela dwuelementowego, ryzyko portfela,

σ²_A, σ²_B - wariancja stóp zwrotu z inwestycji w papier wartościowy A i B odpowiednio,

σ_A, σ_B - odchylenie standardowe stóp zwrotu inwestycji w papier wartościowy (ryzyko) A i B odpowiednio,

ρ_AB - współczynnik korelacji między stopami zwrotu z inwestycji w papier wartościowy A i B.

3. Ryzyko portfela

Oczekiwany zwrot z dwu- lub więcej elementowych portfolio liczony jest jako suma ważona oczekiwanych zwrotów z poszczególnych składowych portfolio.

Natomiast ryzyko portfela papierów wartościowych mierzone odchyleniem standardowym zależny również od siły powiązań między składowymi portfolio, czyli od wartości współczynnika korelacji między tymi składowymi.

Można uzyskać redukcję ryzyka portfolio przez odpowiednią dywersyfikację; przez taki dobór odpowiednich składowych portfolio i ich ilości, by ryzyko portfolio było możliwie najmniejsze. Współczynnik korelacji między stopami zwrotu dwu składników portfolio przyjmuje wartość z przedziału [-1,+1].

Zatem odpowiednia konstrukcja portfela jest zależna od wartości współczynnika korelacji ρ_AB. Dla dwuelementowego portfolio złożonego z aktywów kapitałowych A oraz B, przy założeniu, że
, oczekiwana stopa zwrotu wynosi [6, 57, 119].:

.

Jeśli:

1. ρ_AB = 1, wariancja stopy zwrotu z portfolio wynosi:

,

a odchylenie standardowe, czyli miara ryzyka portfolio σ_AB jest średnią ważoną:

σ_AB=W_Aσ_A+W_Bσ_B. (7.6)

Wówczas, mimo dywersyfikacji, nie uzyska się efektu redukcji ryzyka, zbiór możliwych portfolio przedstawia rysunek 7.27.

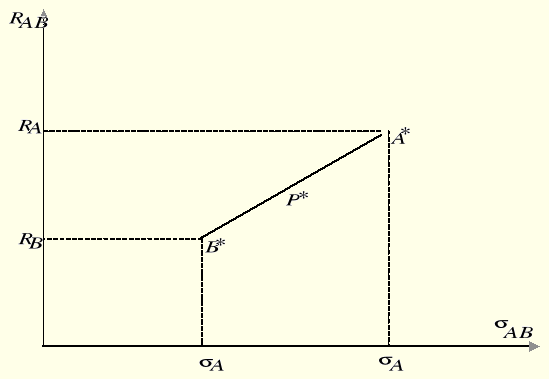
Rys. 7.27. Zbiór możliwych portfeli dla ρ_AB = 1.

2. ρ = -1, wariancja stopy zwrotu portfolio wynosi:

,

a odchylenie standardowe, czyli miara ryzyka portfolio:

(7.7)

Aby ryzyko portfela, złożonego z dwóch papierów A i B, o korelacji ρ_AB= - 1 było równe zero, musi więc być spełnione:

W_Aσ_A − W_Bσ_B=0,

stąd:

W_Aσ_A=W_Bσ_B, lub

W_Aσ_A=(1-W_A)σ_B, lub

(1-W_B)σ_A=W_Bσ_B,

a więc:

lub:

.

Wówczas stopa zwrotu portfolio wynosi

Zbiór rozwiązań dla innych proporcji zainwestowania przedstawia rysunek 7.28.

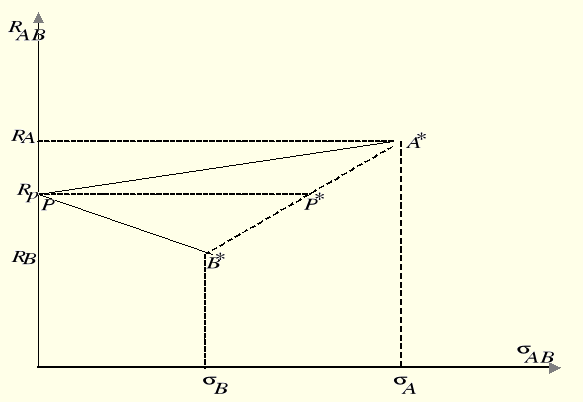
Rys. 7.28. Zbiór możliwych portfeli dla ρ_AB = −1.

Punkt P na osi rzędnych reprezentuje portfel o ryzyku zerowym. Dla portfela złożonego z dwu aktywów, dla których współczynnik korelacji jest równy -1, zawsze można znaleźć taką proporcję zainwestowania w aktywo A i w aktywo B, że skonstruowany portfel będzie się charakteryzował ryzykiem zerowym. Przy czym, jak łatwo zauważyć, stopa zwrotu z portfela będzie niższa (zwykle) niż stopa zwrotu z aktywa A o wysokiej stopie zwrotu, ale wyższa (zwykle) niż stopa zwrotu z aktywa B o niskiej stopie zwrotu.

3. ρ = 0; wariancja stóp zwrotu z portfela wynosi:

,

a odchylenie standardowe:

(7.8)

Różniczkując wyrażenie (7.8) po W_A i pamiętając, że W_B = 1 − W_A oraz przyrównując pochodną do zera, a następnie rozwiązując otrzymane równanie względem W_A, otrzymujemy W_A i W_B, które minimalizują ryzyko (ale nie zerują go) w przypadku ρ_AB = 0:

.

Stopa zwrotu z portfolio wynosi

,

a zbiór rozwiązań przedstawia rysunek 7.29

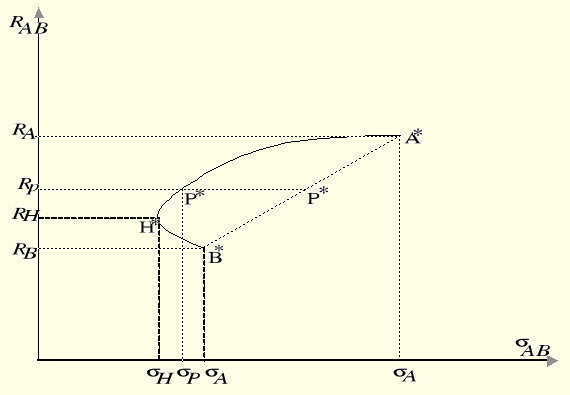
Rys. 7.29. Zbiór możliwych portfeli dla ρ_AB = 0.

Punkt H na rysunku 7.29 reprezentuje portfel o minimalnym ryzyku.

Zbiór wszystkich możliwych rozwiązań dla rozważanego przypadku zawiera się w trójkącie APB (rys. 7.30).

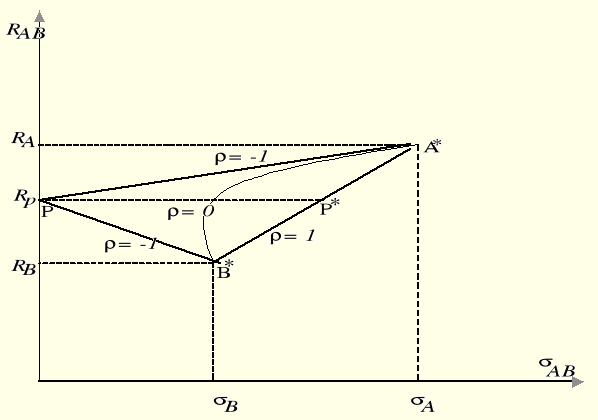
Rys. 7.30. Relacja między stopą zwrotu i ryzykiem portfolio.

Jak wynika z przeprowadzonych rozważań oraz analizy rysunku 7.30, siła redukcji ryzyka zależy od wartości współczynnika korelacji stóp zwrotu z elementów portfolio. Jeśli ρ = 1, ryzyko portfela jest równe ważonej sumie ryzyka składowych portfela. Jeśli
= -1, przez odpowiednią konstrukcję portfela istnieje możliwość bardzo silnej redukcji ryzyka - nawet do zera. Im mniej dodatnio skorelowane stopy zwrotu ze składników portfela, tym większa możliwość redukcji ryzyka.

Co więcej można również pokazać, że im więcej aktywów kapitałowych w portfolio, tym efekt dywersyfikacji będzie większy.

Załóżmy, że portfel zawiera N papierów wartościowych o współczynnikach korelacji wzajemnej między stopami zwrotu ρ_ij = 0, i, j = 1,2,..., N, i > j oraz odchyleniach standardowych σ₁, σ₂,...., σ_N odpowiednio. W takim przypadku ryzyko portfela:

,

gdzie:

* wariancja stóp zwrotu (kwadrat odchylenia standardowego) z portfela złożonego z N papierów,

N * liczba papierów w portfelu,

i * i-ty papier w portfelu, i=1,2,…,N

Jeżeli przyjmiemy
, wówczas:

.

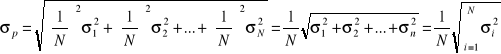
Jeśli dodatkowo założymy, że σ₁=σ₂=…=σ_N, wówczas:

.

Im większe jest N, czyli ilość papierów w portfelu, tym mniejsze jest σ_p, czyli ryzyko portfela.

Dobierając zatem odpowiednią ilość składowych portfolio oraz takie aktywa, dla których współczynniki korelacji są stosunkowo małe, można uzyskać silną redukcję ryzyka. Ryzyko portfolio zależy również od proporcji zainwestowania funduszy w papiery wartościowe A i B.

Przykład 7.2. cd.

Zależność między ryzykiem portfolio a proporcją zainwestowania w A i B dla przypadku rozważanego w przykładzie 7.2 przedstawia rysunek 7.31.

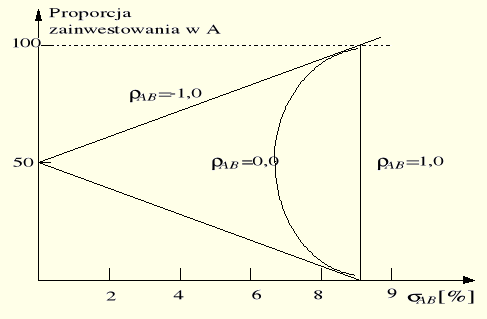
Rys. 7.31. Relacja między ryzykiem portfela a proporcją zainwestowania; σ_A = σ_B = 0,09,
W_A + W_B = 1.

Jeśli korelacja między A i B (w zadaniu 7.2) jest absolutnie negatywna, ryzyko portfolio jest eliminowane tylko wtedy, gdy WA=WB=0,05, to znaczy, gdy fundusz rozdzielony jest równo między oba składniki portfolio o takim samym ryzyku, ponieważ zgodnie ze wzorem (7.7)

A więc również, skoro W_B = 1 − W_A, W_B = 0,5.

Każda inna proporcja zainwestowania w aktywo A i B spowoduje redukcję ryzyka w mniejszym stopniu - ryzyko może przyjmować wartości od 0% do 9% (9% - ryzyko o takiej wartości wystąpi wówczas, gdy cały fundusz zainwestowany zostanie w jeden rodzaj papieru wartościowego).

W przypadku, gdy współczynnik korelacji jest równy zero, ryzyko może być redukowane w zależności od proporcji zainwestowania w poszczególne papiery, na przykład od wielkości WA.

Zgodnie z wyrażeniem (7.8)

Wówczas ryzyko

A więc, najlepszy rezultat, najwyższą redukcję ryzyka uzyska się dla WA =WB = 0,5, dla którego ryzyko jest równe 0,064, czyli 6,4%.

Dla papierów o współczynniku korelacji stóp zwrotu równym 1,0, w rozważanym przypadku, gdy
, nie uzyska się żadnej redukcji ryzyka portfolio, wówczas bowiem, zgodnie z (7.6)

_.

Przedstawiona procedura analizy zachowania się ryzyka portfolio jest stosowana przede wszystkim w portfolio dwuskładnikowym. W rzeczywistości portfolio może być kombinacją większej liczby składników, wówczas ilość obliczeń gwałtownie wzrasta - na przykład do szacowania n−elementowego portfolio należy obliczyć n(n − 1)/2 współczynników korelacji. Pojawia się problem znalezienia takiej kombinacji składników, takiego portfolio papierów wartościowych, które

• minimalizuje ryzyko portfolio przy zadanym poziomie zwrotu, lub

• maksymalizuje zwrot z portfolio przy zadanym poziomie ryzyka.

1. Analiza ryzyka wieloelementowego portfolio

Lokując fundusze w różnego rodzaju aktywa, papiery wartościowe, inwestor spodziewa się zmniejszenia ryzyka związanego z inwestowaniem w jeden typ papieru wartościowego. Większość papierów wartościowych jest dodatnio skorelowana z ogółem rynku papierów wartościowych, nie jest więc możliwe, poprzez dywersyfikację, całkowite wyeliminowanie ryzyka - zredukowanie go do zera.

Zachowanie się rynku papierów wartościowych jest silnie związane z sytuacją gospodarczą kraju. Zwykle, jeśli sytuacja gospodarcza się poprawia, zwroty z większości papierów wartościowych wzrastają, jeśli sytuacja się pogarsza, zwroty maleją. Oprócz tej ogólnej tendencji - "podążania" zwrotów z poszczególnych papierów wartościowych za sytuacją ogólnogospodarczą, obserwuje się również pewne indywidualne wahania wartości stopy zwrotu z papierów wartościowych niezależnie od zachowania się gospodarki.

Wyróżnia się dwa rodzaje ryzyka

• ryzyko systematyczne; niedywersyfikowalne; rynkowe,

• ryzyko niesystematyczne; dywersyfikowalne; specyficzne.

Systematyczne ryzyko odpowiada tej części zmienności zwrotu z indywidualnego papieru wartościowego, której przyczyną są ogólne zmiany rynkowe. Systematyczne ryzyko stanowi 25% - 50% ryzyka jako całości dla każdego papieru wartościowego (wg danych amerykańskich). Źródłami ryzyka systematycznego są:

• zmiany stopy oprocentowania,

• zmiany siły nabywczej pieniędzy,

• zmiany oczekiwań inwestora co do sytuacji gospodarczej,

• zmiany polityczne,

• wahania stopy inflacji,

• konflikty międzynarodowe.

Ryzyko systematyczne nie może być redukowane przez dywersyfikację, jednakże należy je uwzględniać przy szacowaniu premii za ryzyko dla indywidualnego papieru wartościowego.

Niesystematyczne ryzyko jest unikalne dla każdego rodzaju papieru wartościowego. Jest to zmienność stopy zwrotu, której przyczyną są uwarunkowania wewnętrzne firmy, na przykład:

• zdolności i poziom wiedzy menedżerskiej kierownictwa,

• podejmowane decyzje menedżerskie,

• możliwość występowanie strajków załogi,

• stosowane systemy motywacyjne,

• dostępność surowców,

• siła wpływu rządowych ustaw na wydatki niebezpośrednio produkcyjne, na przykład z tytułu kontroli zanieczyszczeń,

• siła wpływu konkurencji,

• poziom jakości wyrobów i usług,

• poziomy dźwigni finansowej i operacyjnej,

Ponieważ niesystematyczne ryzyko jest unikalne dla każdej firmy, istnieje więc możliwość takiego doboru papierów wartościowych różnych firm, aby otrzymać dobrze zdywersyfikowane portfolio skutecznie redukujące ryzyko, redukując ryzyko niesystematyczne, (rys. 7.32).



Rys. 7.32. Niesystematyczne ryzyko i dywersyfikacja portfolio [119].

Oczywiście im większą liczbę różnego typu papierów wartościowych zawiera portfolio, tym mniejsze ryzyko. W rzeczywistości 10 - 15 losowo dobranych składników portfolio stanowi wystarczająco dobrą dywersyfikację; skutecznie eliminuje ryzyko niesystematyczne.




W. Tarczyński „Rynki kapitałowe - metody ilościowe cz. II” Agencja Wydawnicza Placet, Warszawa 1997.

Harry M. Markowitz „The Early History of Portfolio Theory” „Perspectives Financial Analysts Journal” Jully/August 1999

7

10

---