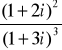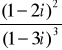Zadanie 1.
Wykonać następujące działania na liczbach zespolonych:
Najprościej zadanie można rozwiązać wykonując kolejno działania w liczniku i mianowniku:
![]()
Można również zadanie rozwiązać mnożąc i dzieląc podane wyrażenie przez liczby sprzężone do liczb występujących w mianowniku ułamka:
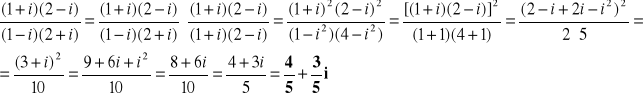
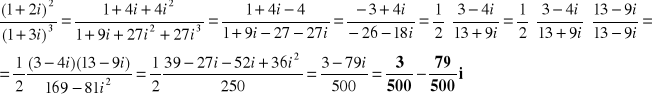
Do rozwiązania wykorzystano znane z algebry elementarnej zależności:
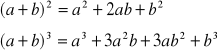
Zadanie 2.
Wykonać następujące działania na liczbach zespolonych:
Korzystając z uwag do zadania 1 a) przeprowadza się odpowiednie obliczenia:
![]()
lub:
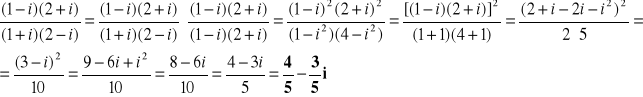
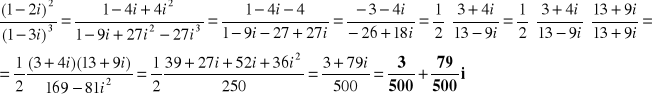
Wykorzystano podstawowe wzory algebraiczne podane w zadaniu 1 b).
Zadanie 3.
Obliczyć pierwiastek kwadratowy z liczby zespolonej:
z = 1 - 3i
Zadanie może być rozwiązane na dwa sposoby.
Pierwszy z nich polega na zastosowaniu postaci trygonometryczne liczby zespolonej i wzoru Moivre'a:
1 - 3i = r(cosϕ +isinϕ)
gdzie:
r = ![]()
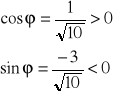
a więc kąt ϕ leży w IV ćwiartce płaszczyzny, czyli spełnia układ nierówności:
270° < ϕ < 360° - wobec czego:
sin(360° - ϕ) = ![]()
⇒ 360° - ϕ = 71,565051° ⇒ ϕ = 288,43495°
Wyżej obliczony kąt stanowi tzw. argument główny - wszystkich argumentów jest nieskończenie wiele i różnią się od siebie o okres funkcji sinus, czyli o 360°.
Można więc napisać:
1 - 3i = ![]()
Należy zwrócić uwagę na sposób zapisu argumentów odpowiednich funkcji - wyniki egzaminów i kolokwiów wykazują, że studenci nieprawidłowo stosują nawiasy.
Dalej można napisać:
![]()
gdzie:
![]()
![]()
i ostatecznie:
![]()
Ponieważ istnieją dwa pierwiastki 2-go stopnia, to pierwszy z nich dostaniemy dla k = 0, a drugi dla k = 1:
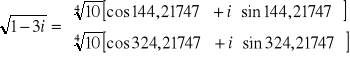
To kończy rozwiązanie matematyczne zadania - można jeszcze obliczyć je numerycznie:
![]()
sin144,21747° ≈ 0,584710
cos144,21747° ≈ -0,811242
sin324,21747° ≈ -0,584710
cos324,21747° ≈ = 0,811242
i
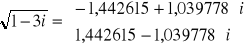
Sprawdzenie:
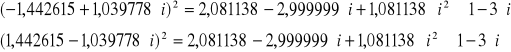
Druga metoda rozwiązania zadania polega na wykorzystaniu definicji pierwiastkowania jako funkcji odwrotnej do potęgowania i nie wymaga sprowadzania liczby do postaci trygonometrycznej.
![]()
Poszukiwana liczba (pierwiastek) posiada część rzeczywistą x i część urojoną y. Po podniesieniu stronami do kwadratu wyjściowej zależności otrzymuje się równanie:
![]()
Dwie liczby zespolone są równe wtedy i tylko wtedy, kiedy mają równe odpowiednio części rzeczywiste i urojone. Dostajemy więc układ równań:
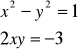
Ponieważ liczba pierwiastkowana jest różna od zera (z ≠ 0), to i jej pierwiastek musi być różny od zera (![]()
), a więc musi być ![]()
- obie części nie mogą być jednocześnie zerami. Przyjmując, że x ≠ 0 można z drugiego równania napisać:
![]()
(gdyby było x = 0 to zawsze można napisać ![]()
)
Podstawiając ostatnią wartość do pierwszego równania otrzymuje się:
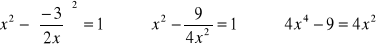
Otrzymujemy więc tzw. równanie dwukwadratowe:
![]()
Po podstawieniu:
![]()
otrzymuje się „zwykłe” równanie kwadratowe:
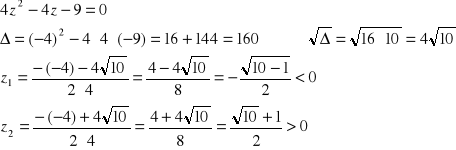
Pierwszy pierwiastek (z1) należy odrzucić ponieważ nie spełnia założenia wyjściowego (z > 0) i ostatecznie:
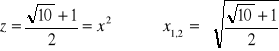
Po podstawieniu do pierwszego równania otrzymujemy:
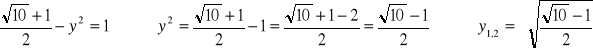
Łącznie dostajemy więc aż 4 kombinacje pierwiastków - wybieramy tylko te które spełniają warunek, że ich iloczyn ma znak taki jaki ma współczynnik części urojonej liczby pierwiastkowanej (dowód na wykładzie), a więc ostatecznie:
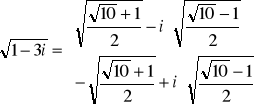
Ostanie wyrażenie kończy matematyczne rozwiązanie zadania. Można je jeszcze obliczyć numerycznie:
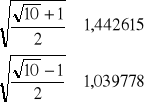
czyli:
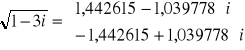
a więc identyczne jak przy rozwiązaniu poprzednią metodą.
Zadanie 4.
Obliczyć pierwiastek kwadratowy z liczby zespolonej:
z = 1 + 3i
Wykorzystamy (tym razem już bez komentarzy) sposób postępowania z zadania 3.
1 + 3i = r(cosϕ +isinϕ)
gdzie:
r = ![]()
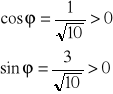
a więc kąt ϕ leży w I ćwiartce płaszczyzny, czyli spełnia układ nierówności:
0° < ϕ < 90° - wobec czego:
sinϕ = ![]()
⇒ ϕ = 71,56505°
1 + 3i = ![]()
![]()
gdzie:
![]()
![]()
i ostatecznie:
![]()
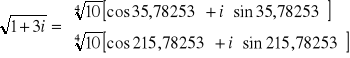
To kończy rozwiązanie matematyczne zadania - można jeszcze obliczyć je numerycznie:
![]()
sin35,78253° ≈ 0,584710
cos35,78253° ≈ 0,811242
sin215,78253° ≈ -0,584710
cos324,21747° ≈ =- 0,811242
i
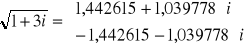
Sprawdzenie:
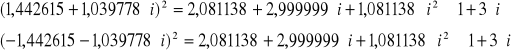
![]()
Dostajemy więc układ równań:
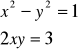
![]()
Podstawiając ostatnią wartość do pierwszego równania otrzymuje się:
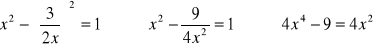
![]()
Po podstawieniu:
![]()
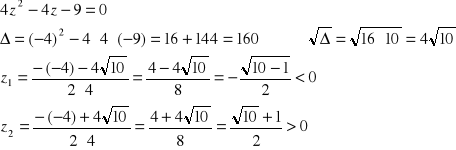
Pierwszy pierwiastek (z1) należy odrzucić ponieważ nie spełnia założenia wyjściowego (z > 0) i ostatecznie:
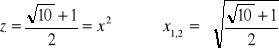
Po podstawieniu do pierwszego równania otrzymujemy:
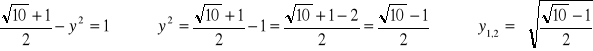
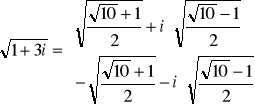
Ostatnie wyrażenie kończy matematyczne rozwiązanie zadania. Można je jeszcze obliczyć numerycznie:
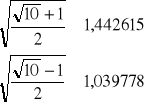
czyli:
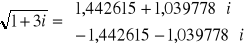
a więc identyczne jak przy rozwiązaniu poprzednią metodą.
Zadanie 5.
Zapisać w postaci trygonometrycznej liczbę zespoloną:
z = -1 - 2i
-1 - 2i = r(cosϕ +isinϕ)
gdzie:
r = ![]()
moduł liczby zespolonej
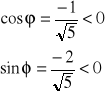
Argument główny liczby zespolonej jest więc kątem w III ćwiartce, czyli:
![]()
sin(180° - ϕ) = -0,894427 ⇒ 180° - ϕ = -63,434949° ⇒ ϕ = 243,434949°
Ostatecznie więc:
-1 - 2i = ![]()
Zadanie 6.
Zapisać w postaci trygonometrycznej liczbę zespoloną:
z = -1 + 2i
Komentarz w zadaniu 5:
-1 + 2i = r(cosϕ +isinϕ)
r = ![]()

Argument główny liczby zespolonej jest więc kątem w IV ćwiartce, czyli:
270° < ϕ < 360°
sin(360° - ϕ) = 0,894427 ⇒ 360° - ϕ = 63,434949° ⇒ ϕ = 296,565051°
Ostatecznie więc:
-1 + 2i = ![]()
Zadanie 7.
Obliczyć czwarty pierwiastek z liczby zespolonej:
z = 1 - i
Najprościej powyższe zadanie można rozwiązać, sprowadzając liczbę pierwiastkowaną do postaci trygonometrycznej i stosując wzór Moivre'a:
![]()
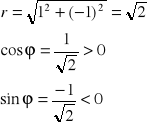
a więc argument główny liczby pierwiastkowanej (z) jest kątem w IV ćwiartce płaszczyzny, czyli spełnia układ nierówności:
270° < ϕ < 360°
sin(360° - ϕ) = -(-![]()
) ⇒ sin(360° - ϕ) = ![]()
⇒ 360° - ϕ = 45° ⇒ ϕ = 315°
Ostatecznie więc:
![]()
Na podstawie wzoru Moivre'a:
![]()
![]()
a wiec pierwiastek jest liczbą zespoloną postaci:
w = ![]()
Istnieją 4 pierwiastki 4-go stopnia z liczby zespolonej - otrzymamy je wstawiając kolejno do powyższego wzoru k = 0, 1, 2, 3;
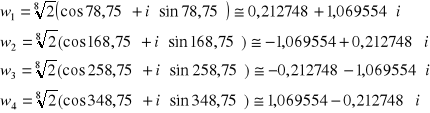
Możliwe jest również rozwiązanie oparte na definicji pierwiastka i nie wymagające sprowadzenia liczby pierwiastkowanej do postaci trygonometrycznej.
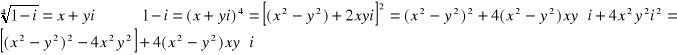
Musi być spełniony układ równań:
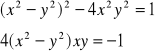
Z drugiego równania:
![]()
Po wstawieniu do pierwszego równania:
![]()
Wykonajmy podstawienie:
![]()
Wówczas otrzymamy równanie kwadratowe ze względu na t:
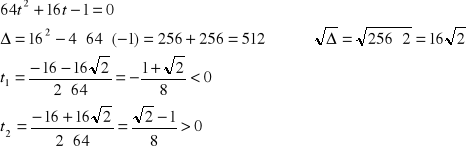
Tylko pierwiastek t2 odpowiada założeniu wyjściowemu, a więc:
![]()
Po wstawieniu do pierwszego równania:
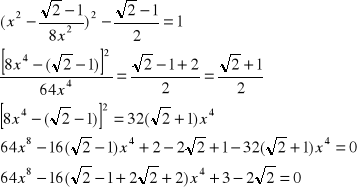
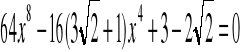
Podstawiamy:
![]()
i otrzymujemy równanie kwadratowe ze względu na u:
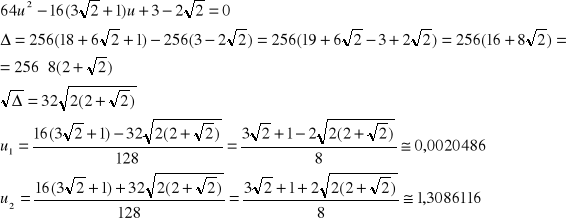
Obydwa pierwiastki są dodatnie, a więc spełniają założenie wyjściowe (u > 0) i ostatecznie:
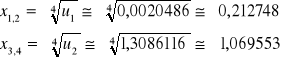

Mamy więc 8 kombinacji dla pierwiastków:

Wszystkie te liczby zespolone spełniają na pewno równanie pierwsze, ponieważ z niego zostały wyprowadzone - należy więc sprawdzić, które spełniają również równanie drugie.
![]()
Jak widać znak iloczynu obu pierwiastków (xy) musi być taki jak znak różnicy (![]()
).
I tak dla:
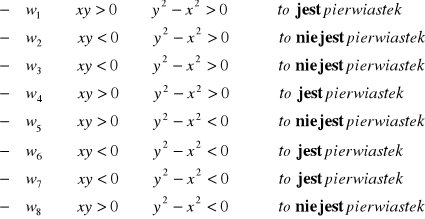
Ostatecznie więc, odrzucając rozwiązania nie spełniające drugiego równania oraz ponownie numerując pierwiastki otrzymuje się:

Otrzymuje się więc te same pierwiastki co w rozwiązaniu a) - należy jednak zauważyć, ze poprzednie rozwiązanie (a) jest dużo prostsze.
Zadanie 8.
Obliczyć czwarty pierwiastek z liczby zespolonej:
z = 1 + i
Komentarze wg zadania 8.
Najprościej powyższe zadanie można rozwiązać, sprowadzając liczbę pierwiastkowaną do postaci trygonometrycznej i stosując wzór Moivre'a:
![]()
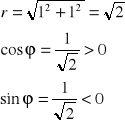
a więc argument główny liczby pierwiastkowanej (z) jest kątem w I ćwiartce płaszczyzny, czyli spełnia układ nierówności:
0° < ϕ < 90°
sin ϕ = ![]()
⇒ ϕ = 45°
Ostatecznie więc:
![]()
Na podstawie wzoru Moivre'a:
![]()
![]()
a wiec pierwiastek jest liczbą zespoloną postaci:
w = ![]()
Istnieją 4 pierwiastki 4-go stopnia z liczby zespolonej - otrzymamy je wstawiając kolejno do powyższego wzoru k = 0, 1, 2, 3;
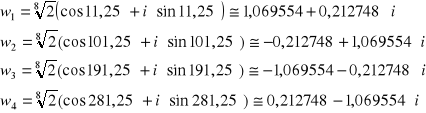
Możliwe jest również rozwiązanie oparte na definicji pierwiastka i nie wymagające sprowadzenia liczby pierwiastkowanej do postaci trygonometrycznej.
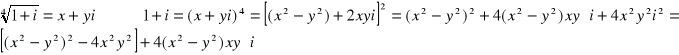
Musi być spełniony układ równań:
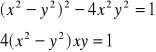
Z drugiego równania:
![]()
Po wstawieniu do pierwszego równania:
![]()
Wykonajmy podstawienie:
![]()
Wówczas otrzymamy równanie kwadratowe ze względu na t:
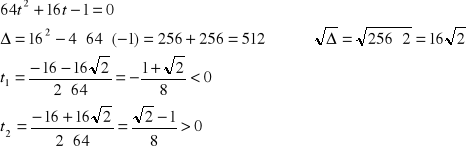
Tylko pierwiastek t2 odpowiada założeniu wyjściowemu, a więc:
![]()
Po wstawieniu do pierwszego równania:
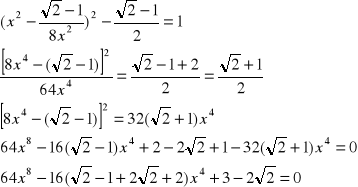
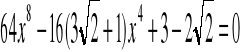
Podstawiamy:
![]()
i otrzymujemy równanie kwadratowe ze względu na u:
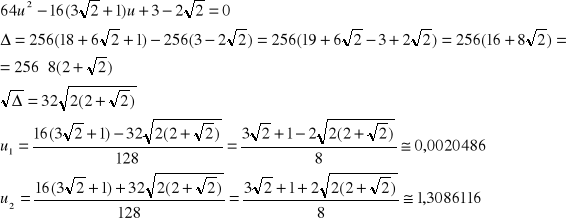
Obydwa pierwiastki są dodatnie, a więc spełniają założenie wyjściowe (u > 0) i ostatecznie:
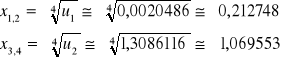

Mamy więc 8 kombinacji dla pierwiastków:

Wszystkie te liczby zespolone spełniają na pewno równanie pierwsze, ponieważ z niego zostały wyprowadzone - należy więc sprawdzić, które spełniają również równanie drugie.
![]()
Jak widać znak iloczynu obu pierwiastków (xy) musi być taki jak znak różnicy (![]()
).
I tak dla:

Ostatecznie więc, odrzucając rozwiązania nie spełniające drugiego równania oraz ponownie numerując pierwiastki otrzymuje się:
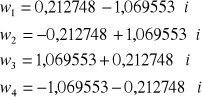
Otrzymuje się więc te same pierwiastki co w rozwiązaniu a) - należy jednak zauważyć, ze poprzednie rozwiązanie (a) jest dużo prostsze.
Zadanie 9.
Obliczyć pierwiastki równania kwadratowego:
![]()
Wyróżnik trójmianu kwadratowego:
![]()
![]()
![]()
Zadanie 10.
Obliczyć pierwiastki równania kwadratowego:
![]()
Wyróżnik trójmianu kwadratowego:
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Liczby zespolone zadania i odpowiedzi cz 2
Liczby zespolone zadania
liczby zespolone zadania, Matematyka
liczby zespolone, zadania z odpowiedziami
liczby zespolone zadania z wykładu1
liczby zespolone zadania 2
Liczby zespolone zadania i odpowiedzi cz 1
ZAdania z matematyki, LICZBY ZESPOLONE 2010, LICZBY ZESPOLONE - ZADANIA
Kusztelak Liczby zespolone Zadania z odpowiedziami
Liczby zespolone zadania
Liczby zespolone L.zespolone-zadania2
więcej podobnych podstron