Algorytmy i Struktury Danych

Wykład 6:

Sortowanie kubełkowe, sortowanie zewn˛etrzne

dr Anna Maria Radzikowska

Wydział Matematyki i Nauk Informacyjnych

Politechnika Warszawska

Projekt wspó

ãfinansowany przez Uniē EuropejskĎ

w ramach Europejskiego Funduszu Spo

ãecznego

dr Anna M. Radzikowska, AiSD, wykład 6

– p.1/28

Sortowanie kubełkowe

dr Anna M. Radzikowska, AiSD, wykład 6

– p.2/28

Sortowanie kubełkowe

Dane jest uniwersum U

= {u

1

, . . . , u

m

}. Rozwa˙zane b˛ed ˛

a ci ˛

agi

A

= (A

1

, . . . , A

n

), przy czym

m

≪ n

.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.3/28

Sortowanie kubełkowe

Dane jest uniwersum U

= {u

1

, . . . , u

m

}. Rozwa˙zane b˛ed ˛

a ci ˛

agi

A

= (A

1

, . . . , A

n

), przy czym

m

≪ n

.

Zatem w rozwa˙zanych ci ˛

agach wiele elementów b˛edzie si˛e powtarza´c.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.3/28

Sortowanie kubełkowe

Dane jest uniwersum U

= {u

1

, . . . , u

m

}. Rozwa˙zane b˛ed ˛

a ci ˛

agi

A

= (A

1

, . . . , A

n

), przy czym

m

≪ n

.

Zatem w rozwa˙zanych ci ˛

agach wiele elementów b˛edzie si˛e powtarza´c.

Zastosowanie jakiegokolwiek algorytmu sortowania przez porównania

spowoduje, ze wielokrotnie b˛ed ˛

a porównywane elementy o tych samych

kluczach — to powoduje nieefektywno´s´c post˛epowania.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.3/28

Sortowanie kubełkowe (cd.)

Idea algorytmu:

dr Anna M. Radzikowska, AiSD, wykład 6

– p.4/28

Sortowanie kubełkowe (cd.)

Idea algorytmu:

Inicjujemy m pustych kolejek (kubełków).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.4/28

Sortowanie kubełkowe (cd.)

Idea algorytmu:

Inicjujemy m pustych kolejek (kubełków).

Przegl ˛

adamy ci ˛

ag wej´sciowy A wstawiaj ˛

ac kolejne elementy A

i

do kolejki o indeksie A

i

.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.4/28

Sortowanie kubełkowe (cd.)

Idea algorytmu:

Inicjujemy m pustych kolejek (kubełków).

Przegl ˛

adamy ci ˛

ag wej´sciowy A wstawiaj ˛

ac kolejne elementy A

i

do kolejki o indeksie A

i

.

Scalamy tak utworzone kolejki.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.4/28

Sortowanie kubełkowe (cd.)

Idea algorytmu:

Inicjujemy m pustych kolejek (kubełków).

Przegl ˛

adamy ci ˛

ag wej´sciowy A wstawiaj ˛

ac kolejne elementy A

i

do kolejki o indeksie A

i

.

Scalamy tak utworzone kolejki.

Kopiujemy elementy z utworzonej kolejki do oryginalnej

tablicy A.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.4/28

Sorowanie kubełkowe (cd.)

Zakładamy, ˙ze dane s ˛

a nast˛epuj ˛

ace deklaracje:

Q : array

[1..m] of queue;

{tablica m kolejek}

Init

(q) — inicjalizacja kolejki q.

Insert

(q, x) — wstaw element x do kolejki q.

Concatenate

(q

1

, q

2

) — zł ˛

acz kolejki q

1

i q

2

tworz ˛

ac zmodyfikowan ˛

a

kolejk˛e q

1

(tzn. do kolejki q

1

doł ˛

acz kolejk˛e q

2

, wynikowa kolejka na q

1

).

DeQueue

(q) — usu´n pierwszy element z kolejki q.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.5/28

Sortowanie kubełkowe — algorytm

1

begin

2

for i

:= 1 to m do Init(Q

i

) od;

3

for i

:= 1 to n do Insert(A

i

, Q

A

i

) od;

4

for i

:= 2 to m do Concatenate(Q

1

, Q

i

) od;

5

for i

:= 1 to n do A

i

:=DeQueue(Q

1

) od;

6

end;

dr Anna M. Radzikowska, AiSD, wykład 6

– p.6/28

Zło˙zono´s´c czasowa

Koszt ka˙zdej operacji kolejkowej —

Θ(1)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.7/28

Zło˙zono´s´c czasowa

Koszt ka˙zdej operacji kolejkowej —

Θ(1)

P˛etla (2) obróci si˛e m razy — koszt tej p˛etli

Θ(m)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.7/28

Zło˙zono´s´c czasowa

Koszt ka˙zdej operacji kolejkowej —

Θ(1)

P˛etla (2) obróci si˛e m razy — koszt tej p˛etli

Θ(m)

P˛etla (3) obróci si˛e n razy — jej koszt

Θ(n)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.7/28

Zło˙zono´s´c czasowa

Koszt ka˙zdej operacji kolejkowej —

Θ(1)

P˛etla (2) obróci si˛e m razy — koszt tej p˛etli

Θ(m)

P˛etla (3) obróci si˛e n razy — jej koszt

Θ(n)

P˛etla (4) obróci si˛e m

− 1 razy — jej koszt Θ(m)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.7/28

Zło˙zono´s´c czasowa

Koszt ka˙zdej operacji kolejkowej —

Θ(1)

P˛etla (2) obróci si˛e m razy — koszt tej p˛etli

Θ(m)

P˛etla (3) obróci si˛e n razy — jej koszt

Θ(n)

P˛etla (4) obróci si˛e m

− 1 razy — jej koszt Θ(m)

P˛etla (5) obróci si˛e n razy — jej koszt

Θ(n).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.7/28

Zło˙zono´s´c czasowa

Koszt ka˙zdej operacji kolejkowej —

Θ(1)

P˛etla (2) obróci si˛e m razy — koszt tej p˛etli

Θ(m)

P˛etla (3) obróci si˛e n razy — jej koszt

Θ(n)

P˛etla (4) obróci si˛e m

− 1 razy — jej koszt Θ(m)

P˛etla (5) obróci si˛e n razy — jej koszt

Θ(n).

Zatem T

(n) = C

1

n

+ C

2

n

+ C

3

m

+ C

4

n, czyli T

(n) = Θ(n).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.7/28

Sortowanie zewn˛etrzne

dr Anna M. Radzikowska, AiSD, wykład 6

– p.8/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porzadkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porzadkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (3, 6, 8, 9, 12)

B

= (1, 2, 4, 5, 7, 10, 11).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (3, 6, 8, 9, 12)

B

= (1, 2, 4, 5, 7, 10, 11).

Ci ˛

ag wynikowy: C

=

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (3, 6, 8, 9, 12)

B

= (2, 4, 5, 7, 10, 11).

Ci ˛

ag wynikowy: C

= (1)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (3, 6, 8, 9, 12)

B

= (4, 5, 7, 10, 11).

Ci ˛

ag wynikowy: C

= (1, 2)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (6, 8, 9, 12)

B

= (4, 5, 7, 10, 11).

Ci ˛

ag wynikowy: C

= (1, 2, 3)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (6, 8, 9, 12)

B

= (5, 7, 10, 11).

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (6, 8, 9, 12)

B

= (7, 10, 11).

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (8, 9, 12)

B

= (7, 10, 11).

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (8, 9, 12)

B

= (10, 11).

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6, 7)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (9, 12)

B

= (10, 11).

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6, 7, 8)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (12)

B

= (10, 11).

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6, 7, 8, 9)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (12)

B

= (11).

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= (12)

B

= ().

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= ()

B

= ().

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego

Sortowanie zewn˛etrzne

— porz ˛

adkowanie ci ˛

agów zapisanych na plikach i nie

mieszcz ˛

acych si˛e w pami˛eci wewn˛etrznej.

Scalanie

(ang. merge) — ł ˛

aczenie kilku ci ˛

agów uporz ˛

adkowanych w jeden

ci ˛

ag uporz ˛

adkowany.

Przykład 6.1

Dane s ˛

a dwa ci ˛

agi

A

= ()

B

= ().

Ci ˛

ag wynikowy: C

= (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)

W sortowaniu zewn˛etrznym wykorzystuje si˛e pliki pomocnicze.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.9/28

Idea sortowania zewn˛etrznego (cd.)

Dany jest ci ˛

ag A

= (A

1

, . . . , A

N

) elementów uniwersum U zapisany na pliku.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.10/28

Idea sortowania zewn˛etrznego (cd.)

Dany jest ci ˛

ag A

= (A

1

, . . . , A

N

) elementów uniwersum U zapisany na pliku.

Blok

— pewien posortowany podci ˛

ag ci ˛

agu A.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.10/28

Idea sortowania zewn˛etrznego (cd.)

Dany jest ci ˛

ag A

= (A

1

, . . . , A

N

) elementów uniwersum U zapisany na pliku.

Blok

— pewien posortowany podci ˛

ag ci ˛

agu A.

Przykład 6.2

W ci ˛

agu A

= (3, 5, 6, 7, 9, 1, 4, 8, 10, 2, 12) wyst˛epuj ˛

a 3 najdłu˙zsze bloki:

(3, 5, 6, 7, 9), (1, 4, 8, 10), (2, 12).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.10/28

Idea sortowania zewn˛etrznego (cd.)

Dany jest ci ˛

ag A

= (A

1

, . . . , A

N

) elementów uniwersum U zapisany na pliku.

Blok

— pewien posortowany podci ˛

ag ci ˛

agu A.

Przykład 6.2

W ci ˛

agu A

= (3, 5, 6, 7, 9, 1, 4, 8, 10, 2, 12) wyst˛epuj ˛

a 3 najdłu˙zsze bloki:

(3, 5, 6, 7, 9), (1, 4, 8, 10), (2, 12).

Metody sortowania zewn˛etrznego obejmuj ˛

a zwykle 2 główne etapy:

tworzenie bloków pocz ˛

atkowych i ich dystrybucja do plików

pomocniczych

scalanie bloków pobieranych z plików pomocniczych do chwili

utworzenia 1 bloku.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.10/28

Ł ˛

aczenie proste — metoda 1

Zakładamy, ˙ze dane wej´sciowe zapisane s ˛

a na pliku p

0

i dysponujemy k

plikami pomocniczymi p

1

, . . . , p

k

.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.11/28

Ł ˛

aczenie proste — metoda 1

Zakładamy, ˙ze dane wej´sciowe zapisane s ˛

a na pliku p

0

i dysponujemy k

plikami pomocniczymi p

1

, . . . , p

k

.

1. Najprostsza metoda:

dr Anna M. Radzikowska, AiSD, wykład 6

– p.11/28

Ł ˛

aczenie proste — metoda 1

Zakładamy, ˙ze dane wej´sciowe zapisane s ˛

a na pliku p

0

i dysponujemy k

plikami pomocniczymi p

1

, . . . , p

k

.

1. Najprostsza metoda:

(i)

d

:= 1

{d – długo´s´c aktualnego bloku}

dr Anna M. Radzikowska, AiSD, wykład 6

– p.11/28

Ł ˛

aczenie proste — metoda 1

Zakładamy, ˙ze dane wej´sciowe zapisane s ˛

a na pliku p

0

i dysponujemy k

plikami pomocniczymi p

1

, . . . , p

k

.

1. Najprostsza metoda:

(i)

d

:= 1

{d – długo´s´c aktualnego bloku}

(ii)

bloki długo´sci d przenosimy kolejno na pliki p

1

, . . . , p

k

, p

1

, . . .

dr Anna M. Radzikowska, AiSD, wykład 6

– p.11/28

Ł ˛

aczenie proste — metoda 1

Zakładamy, ˙ze dane wej´sciowe zapisane s ˛

a na pliku p

0

i dysponujemy k

plikami pomocniczymi p

1

, . . . , p

k

.

1. Najprostsza metoda:

(i)

d

:= 1

{d – długo´s´c aktualnego bloku}

(ii)

bloki długo´sci d przenosimy kolejno na pliki p

1

, . . . , p

k

, p

1

, . . .

(iii)

scalamy po 1 bloku z plików pomocniczych zapisuj ˛

ac blok wynikowy na

p

0

dr Anna M. Radzikowska, AiSD, wykład 6

– p.11/28

Ł ˛

aczenie proste — metoda 1

Zakładamy, ˙ze dane wej´sciowe zapisane s ˛

a na pliku p

0

i dysponujemy k

plikami pomocniczymi p

1

, . . . , p

k

.

1. Najprostsza metoda:

(i)

d

:= 1

{d – długo´s´c aktualnego bloku}

(ii)

bloki długo´sci d przenosimy kolejno na pliki p

1

, . . . , p

k

, p

1

, . . .

(iii)

scalamy po 1 bloku z plików pomocniczych zapisuj ˛

ac blok wynikowy na

p

0

(iv)

d

:= k·d

dr Anna M. Radzikowska, AiSD, wykład 6

– p.11/28

Ł ˛

aczenie proste — metoda 1

Zakładamy, ˙ze dane wej´sciowe zapisane s ˛

a na pliku p

0

i dysponujemy k

plikami pomocniczymi p

1

, . . . , p

k

.

1. Najprostsza metoda:

(i)

d

:= 1

{d – długo´s´c aktualnego bloku}

(ii)

bloki długo´sci d przenosimy kolejno na pliki p

1

, . . . , p

k

, p

1

, . . .

(iii)

scalamy po 1 bloku z plików pomocniczych zapisuj ˛

ac blok wynikowy na

p

0

(iv)

d

:= k·d

(v)

powtarzamy czynno´sci

(ii)

–

(iv)

do chwili, gdy na p

0

b˛edzie 1 blok.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.11/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: (3, 9, 7, 1, 8, 2, 5, 4, 6)

p

1

:

p

2

:

p

3

:

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: (1, 8, 2, 5, 4, 6)

p

1

: 3 |

p

2

: 9 |

p

3

: 7 |

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: (5, 4, 6)

p

1

: 3 | 1 |

p

2

: 9 | 8 |

p

3

: 7 | 2 |

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: ()

p

1

: 3 | 1 | 5 |

p

2

: 9 | 8 | 4 |

p

3

: 7 | 2 | 6 |

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: (3, 7, 9 |)

p

1

: 1 | 5 |

p

2

: 8 | 4 |

p

3

: 2 | 6 |

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: (3, 7, 9 | 1, 2, 8 |)

p

1

: 5 |

p

2

: 4 |

p

3

: 6 |

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: (3, 7, 9 | 1, 2, 8 | 4, 5, 6)

p

1

: ()

p

2

: ()

p

3

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: ()

p

1

: (3, 7, 9)

p

2

: (1, 2, 8)

p

3

: (4, 5, 6)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Przykład 6.3

Niech k

= 3.

p

0

: (1, 2, 3, 4, 5, 6, 7, 8, 9)

p

1

: ()

p

2

: ()

p

3

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.12/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Metoda mało efektywna — ka˙zdy blok jest dwukrotnie kopiowany:

raz w fazie dystrybucji na pliki pomocnicze,

drugi raz w fazie scalania.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.13/28

Ł ˛

aczenie proste — metoda 1 (cd.)

Metoda mało efektywna — ka˙zdy blok jest dwukrotnie kopiowany:

raz w fazie dystrybucji na pliki pomocnicze,

drugi raz w fazie scalania.

Udoskonalenie —- poł ˛

aczenie fazy dystrubucji z faz ˛

a sortowania.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.13/28

Ł ˛

aczenie proste — metoda 2

Mamy

2k − 1 plików pomocniczych. Dane wej´sciowe na pliku p

0

.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.14/28

Ł ˛

aczenie proste — metoda 2

Mamy

2k − 1 plików pomocniczych. Dane wej´sciowe na pliku p

0

.

Algorytm:

(i)

d

:= 1

{ d — aktualna długo´s´c bloku}

dr Anna M. Radzikowska, AiSD, wykład 6

– p.14/28

Ł ˛

aczenie proste — metoda 2

Mamy

2k − 1 plików pomocniczych. Dane wej´sciowe na pliku p

0

.

Algorytm:

(i)

d

:= 1

{ d — aktualna długo´s´c bloku}

(ii)

bloki długo´sci d przenosimy z p

0

na pliki pomocnicze

p

k

, p

k+1

, . . . , p

2

k−1

, p

k

, . . .

dr Anna M. Radzikowska, AiSD, wykład 6

– p.14/28

Ł ˛

aczenie proste — metoda 2

Mamy

2k − 1 plików pomocniczych. Dane wej´sciowe na pliku p

0

.

Algorytm:

(i)

d

:= 1

{ d — aktualna długo´s´c bloku}

(ii)

bloki długo´sci d przenosimy z p

0

na pliki pomocnicze

p

k

, p

k+1

, . . . , p

2

k−1

, p

k

, . . .

(iii)

scalamy po 1 bloku długo´sci d z plików p

k

, . . . , p

2

k−1

umieszczaj ˛

ac boki

wynikowe kolejno na p

0

, . . . , p

k−1

.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.14/28

Ł ˛

aczenie proste — metoda 2

Mamy

2k − 1 plików pomocniczych. Dane wej´sciowe na pliku p

0

.

Algorytm:

(i)

d

:= 1

{ d — aktualna długo´s´c bloku}

(ii)

bloki długo´sci d przenosimy z p

0

na pliki pomocnicze

p

k

, p

k+1

, . . . , p

2

k−1

, p

k

, . . .

(iii)

scalamy po 1 bloku długo´sci d z plików p

k

, . . . , p

2

k−1

umieszczaj ˛

ac boki

wynikowe kolejno na p

0

, . . . , p

k−1

.

(iv)

zmieniamy nazwy plików przyjmuj ˛

ac p

k

:= p

0

, . . . , p

2

k−1

:= p

k−1

odwracaj ˛

ac rol˛e plików wej´sciowch i wyj´sciowych.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.14/28

Ł ˛

aczenie proste — metoda 2

Mamy

2k − 1 plików pomocniczych. Dane wej´sciowe na pliku p

0

.

Algorytm:

(i)

d

:= 1

{ d — aktualna długo´s´c bloku}

(ii)

bloki długo´sci d przenosimy z p

0

na pliki pomocnicze

p

k

, p

k+1

, . . . , p

2

k−1

, p

k

, . . .

(iii)

scalamy po 1 bloku długo´sci d z plików p

k

, . . . , p

2

k−1

umieszczaj ˛

ac boki

wynikowe kolejno na p

0

, . . . , p

k−1

.

(iv)

zmieniamy nazwy plików przyjmuj ˛

ac p

k

:= p

0

, . . . , p

2

k−1

:= p

k−1

odwracaj ˛

ac rol˛e plików wej´sciowch i wyj´sciowych.

(v)

powtarzamy czynno´sci

(iii)

–

(iv)

do chwili, a˙z na p

0

(ew. p

k

)

b˛edzie 1 blok, a pliki pomocnicze b˛eda puste.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.14/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Przykład 6.4

dr Anna M. Radzikowska, AiSD, wykład 6

– p.15/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Przykład 6.4

Niech k

= 2.

p

0

= (3, 8, 10, 21, 12, 4, 2, 11, 18, 9, 20, 7, 1, 5, 25, 15)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.15/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Przykład 6.4

Niech k

= 2.

p

0

= (3, 8, 10, 21, 12, 4, 2, 11, 18, 9, 20, 7, 1, 5, 25, 15)

Faza 1.

p

2

: 3 | 10 | 12 |2 | 18 | 20 | 1 | 25

p

3

: 8 | 21 | 4 | 11 | 9 | 7 | 5 | 15

dr Anna M. Radzikowska, AiSD, wykład 6

– p.15/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Przykład 6.4

Niech k

= 2.

p

0

= (3, 8, 10, 21, 12, 4, 2, 11, 18, 9, 20, 7, 1, 5, 25, 15)

Faza 1.

p

2

: 3 | 10 | 12 |2 | 18 | 20 | 1 | 25

p

3

: 8 | 21 | 4 | 11 | 9 | 7 | 5 | 15

Faza 2.

p

2

(p

0

) : 3, 8 | 4, 12 | 9, 18 | 1, 5

p

3

(p

1

) : 10, 21 | 2, 11 | 7, 20 | 15, 25

dr Anna M. Radzikowska, AiSD, wykład 6

– p.15/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Faza 2.

p

2

(p

0

) : 3, 8 | 4, 12 | 9, 18 | 1, 5

p

3

(p

1

) : 10, 21 | 2, 11 | 7, 20 | 15, 25

dr Anna M. Radzikowska, AiSD, wykład 6

– p.16/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Faza 2.

p

2

(p

0

) : 3, 8 | 4, 12 | 9, 18 | 1, 5

p

3

(p

1

) : 10, 21 | 2, 11 | 7, 20 | 15, 25

Faza 3.

p

2

: 3, 8, 10, 21 | 7, 9, 18, 20

p

3

: 2, 4, 11, 12 | 1, 5, 15, 25

dr Anna M. Radzikowska, AiSD, wykład 6

– p.16/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Faza 2.

p

2

(p

0

) : 3, 8 | 4, 12 | 9, 18 | 1, 5

p

3

(p

1

) : 10, 21 | 2, 11 | 7, 20 | 15, 25

Faza 3.

p

2

: 3, 8, 10, 21 | 7, 9, 18, 20

p

3

: 2, 4, 11, 12 | 1, 5, 15, 25

Faza 4.

p

2

(p

0

) : 2, 3, 4, 8, 10, 11, 12, 21

p

3

(p

1

) : 1, 5, 7, 9, 15, 18, 20, 25

dr Anna M. Radzikowska, AiSD, wykład 6

– p.16/28

Ł ˛

aczenie proste — metoda 2 (cd.)

Faza 2.

p

2

(p

0

) : 3, 8 | 4, 12 | 9, 18 | 1, 5

p

3

(p

1

) : 10, 21 | 2, 11 | 7, 20 | 15, 25

Faza 3.

p

2

: 3, 8, 10, 21 | 7, 9, 18, 20

p

3

: 2, 4, 11, 12 | 1, 5, 15, 25

Faza 4.

p

2

(p

0

) : 2, 3, 4, 8, 10, 11, 12, 21

p

3

(p

1

) : 1, 5, 7, 9, 15, 18, 20, 25

Faza 5.

p

2

: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 15, 18, 20, 21, 25

p

3

: ().

dr Anna M. Radzikowska, AiSD, wykład 6

– p.16/28

Łaczenie naturalne

W obu poprzednich metodach nie wykorzystujemy ewentualnego

cz˛e´sciowego uporz ˛

adkowania pliku ´zródłowego.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.17/28

Łaczenie naturalne

W obu poprzednich metodach nie wykorzystujemy ewentualnego

cz˛e´sciowego uporz ˛

adkowania pliku ´zródłowego.

Metody ł ˛

aczenia naturalnego działaj ˛

a analogicznie do metod ł ˛

aczenia

prostego z tym, ˙ze bloki pocz ˛

atkowe to najdłu˙zsze podci ˛

agi

uporz ˛

adkowane pliku wej´sciowego.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.17/28

Łaczenie naturalne

W obu poprzednich metodach nie wykorzystujemy ewentualnego

cz˛e´sciowego uporz ˛

adkowania pliku ´zródłowego.

Metody ł ˛

aczenia naturalnego działaj ˛

a analogicznie do metod ł ˛

aczenia

prostego z tym, ˙ze bloki pocz ˛

atkowe to najdłu˙zsze podci ˛

agi

uporz ˛

adkowane pliku wej´sciowego.

W konsekwencji, na ogół

dr Anna M. Radzikowska, AiSD, wykład 6

– p.17/28

Łaczenie naturalne

W obu poprzednich metodach nie wykorzystujemy ewentualnego

cz˛e´sciowego uporz ˛

adkowania pliku ´zródłowego.

Metody ł ˛

aczenia naturalnego działaj ˛

a analogicznie do metod ł ˛

aczenia

prostego z tym, ˙ze bloki pocz ˛

atkowe to najdłu˙zsze podci ˛

agi

uporz ˛

adkowane pliku wej´sciowego.

W konsekwencji, na ogół

bloki pocz ˛

atkowe maj ˛

a ró˙zn ˛

a długo´s´c

dr Anna M. Radzikowska, AiSD, wykład 6

– p.17/28

Łaczenie naturalne

W obu poprzednich metodach nie wykorzystujemy ewentualnego

cz˛e´sciowego uporz ˛

adkowania pliku ´zródłowego.

Metody ł ˛

aczenia naturalnego działaj ˛

a analogicznie do metod ł ˛

aczenia

prostego z tym, ˙ze bloki pocz ˛

atkowe to najdłu˙zsze podci ˛

agi

uporz ˛

adkowane pliku wej´sciowego.

W konsekwencji, na ogół

bloki pocz ˛

atkowe maj ˛

a ró˙zn ˛

a długo´s´c

wyst˛epuje mniej faz.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.17/28

Łaczenie naturalne

W obu poprzednich metodach nie wykorzystujemy ewentualnego

cz˛e´sciowego uporz ˛

adkowania pliku ´zródłowego.

Metody ł ˛

aczenia naturalnego działaj ˛

a analogicznie do metod ł ˛

aczenia

prostego z tym, ˙ze bloki pocz ˛

atkowe to najdłu˙zsze podci ˛

agi

uporz ˛

adkowane pliku wej´sciowego.

W konsekwencji, na ogół

bloki pocz ˛

atkowe maj ˛

a ró˙zn ˛

a długo´s´c

wyst˛epuje mniej faz.

Nale˙zy tu uwzgl˛edni´c przypadek “sklejania si˛e” bloków pocz ˛

atkowych –

kolejny blok na pliku pomocniczym rozpoczyna si˛e od elementu

wi˛ekszego od ostatniego elementu poprzedniego bloku na tym pliku.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.17/28

Ł ˛

aczenie naturalne (cd.)

Przykład 6.4 (cd.)

p

0

= (3, 8, 10, 21, 12, 4, 2, 11, 18, 9, 20, 7, 1, 5, 25, 15).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.18/28

Ł ˛

aczenie naturalne (cd.)

Przykład 6.4 (cd.)

p

0

= (3, 8, 10, 21, 12, 4, 2, 11, 18, 9, 20, 7, 1, 5, 25, 15).

Faza 1.

p

2

: 3, 8, 10, 21 | 4

|

9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7

|

15

dr Anna M. Radzikowska, AiSD, wykład 6

– p.18/28

Ł ˛

aczenie naturalne (cd.)

Przykład 6.4 (cd.)

p

0

= (3, 8, 10, 21, 12, 4, 2, 11, 18, 9, 20, 7, 1, 5, 25, 15).

Faza 1.

p

2

: 3, 8, 10, 21 | 4

|

9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7

|

15

Zauwa˙zmy, ˙ze na pliku p

2

blok 2 “skleja si˛e” z blokiem 3. Podobnie na pliku

p

3

blok 3 z blokiem 4.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.18/28

Ł ˛

aczenie naturalne (cd.)

Przykład 6.4 (cd.)

p

0

= (3, 8, 10, 21, 12, 4, 2, 11, 18, 9, 20, 7, 1, 5, 25, 15).

Faza 1.

p

2

: 3, 8, 10, 21 | 4

|

9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7

|

15

Zauwa˙zmy, ˙ze na pliku p

2

blok 2 “skleja si˛e” z blokiem 3. Podobnie na pliku

p

3

blok 3 z blokiem 4.

Faza 1 (poprawiona).

p

2

: 3, 8, 10, 21 | 4, 9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7, 15.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.18/28

Ł ˛

aczenie naturalne (cd.)

Faza 1.

p

2

: 3, 8, 10, 21 | 4, 9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7, 15.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.19/28

Ł ˛

aczenie naturalne (cd.)

Faza 1.

p

2

: 3, 8, 10, 21 | 4, 9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7, 15.

Faza 2.

p

0

: 3, 8, 10, 12, 21 | 1, 5, 7, 15, 25

p

1

: 2, 4, 9, 11, 18, 20.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.19/28

Ł ˛

aczenie naturalne (cd.)

Faza 1.

p

2

: 3, 8, 10, 21 | 4, 9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7, 15.

Faza 2.

p

0

: 3, 8, 10, 12, 21 | 1, 5, 7, 15, 25

p

1

: 2, 4, 9, 11, 18, 20.

Faza 3.

p

2

: 2, 3, 4, 8, 9, 10, 11, 12, 18, 20, 21

p

3

: 1, 5, 7, 15, 25.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.19/28

Ł ˛

aczenie naturalne (cd.)

Faza 1.

p

2

: 3, 8, 10, 21 | 4, 9, 20 | 1, 5, 25

p

3

: 12 | 2, 11, 18 | 7, 15.

Faza 2.

p

0

: 3, 8, 10, 12, 21 | 1, 5, 7, 15, 25

p

1

: 2, 4, 9, 11, 18, 20.

Faza 3.

p

2

: 2, 3, 4, 8, 9, 10, 11, 12, 18, 20, 21

p

3

: 1, 5, 7, 15, 25.

Faza 4.

p

0

: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 15, 18, 20, 21, 25

p

1

: ().

dr Anna M. Radzikowska, AiSD, wykład 6

– p.19/28

Metoda 3

Dane wej´sciowe na pliku p

0

. Mamy

2k − 1 plików pomocniczych.

Kolejna metoda uwzgl˛ednia sposób tworzenia bloków pocz ˛

atkowych.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.20/28

Metoda 3

Dane wej´sciowe na pliku p

0

. Mamy

2k − 1 plików pomocniczych.

Kolejna metoda uwzgl˛ednia sposób tworzenia bloków pocz ˛

atkowych.

Algorytm:

1

begin

2

i

:= k

{ i – numer aktualnego pliku pomocniczego}

3

while

¬ eof(p

0

) do

4

we´z m elementów z p

0

;

5

posortuj je jednym ze znanych algorytmów sortowania tablic;

6

prze´slij utworzony blok na plik pomocniczy p

i

;

7

i

:= k + ((i + 1) mod k)

8

od;

9

end;

dr Anna M. Radzikowska, AiSD, wykład 6

– p.20/28

Metoda 3 (cd.)

Teraz bloki maj ˛

a (teoretycznie) jednakow ˛

a długo´s´c m.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.21/28

Metoda 3 (cd.)

Teraz bloki maj ˛

a (teoretycznie) jednakow ˛

a długo´s´c m.

Je´sli uwzgl˛ednimy przypadek “sklejania si˛e” bloków, mo˙zna wykorzysta´c

tablic˛e k–elementow ˛

a, w której zapami˛etane b˛ed ˛

a ostatnie elementy

bloków na plikach pomocniczych.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.21/28

Metoda 4

W tej metodzie wykorzystujemy struktur˛e kopca z odwróconym

porz ˛

adkiem — teraz element minimalny jest w korzeniu.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.22/28

Metoda 4

W tej metodzie wykorzystujemy struktur˛e kopca z odwróconym

porz ˛

adkiem — teraz element minimalny jest w korzeniu.

Celem jest uzyskanie mo˙zliwie najdłu˙zszych bloków pocz ˛

atkowych.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.22/28

Metoda 4

W tej metodzie wykorzystujemy struktur˛e kopca z odwróconym

porz ˛

adkiem — teraz element minimalny jest w korzeniu.

Celem jest uzyskanie mo˙zliwie najdłu˙zszych bloków pocz ˛

atkowych.

Z ka˙zdym elementem kopca zwi ˛

azany jest dodatkowy atrybut nr b˛ed ˛

acy

numerem bloku odpowiadaj ˛

acemu temu elementowi. Teraz relacja

porz ˛

adku < ma posta´c:

Niech E

1

= (e

1

, n

1

) i E

2

= (e

2

, n

2

) b˛ed ˛

a dwoma elementami. E

1

< E

2

wtt gdy

dr Anna M. Radzikowska, AiSD, wykład 6

– p.22/28

Metoda 4

W tej metodzie wykorzystujemy struktur˛e kopca z odwróconym

porz ˛

adkiem — teraz element minimalny jest w korzeniu.

Celem jest uzyskanie mo˙zliwie najdłu˙zszych bloków pocz ˛

atkowych.

Z ka˙zdym elementem kopca zwi ˛

azany jest dodatkowy atrybut nr b˛ed ˛

acy

numerem bloku odpowiadaj ˛

acemu temu elementowi. Teraz relacja

porz ˛

adku < ma posta´c:

Niech E

1

= (e

1

, n

1

) i E

2

= (e

2

, n

2

) b˛ed ˛

a dwoma elementami. E

1

< E

2

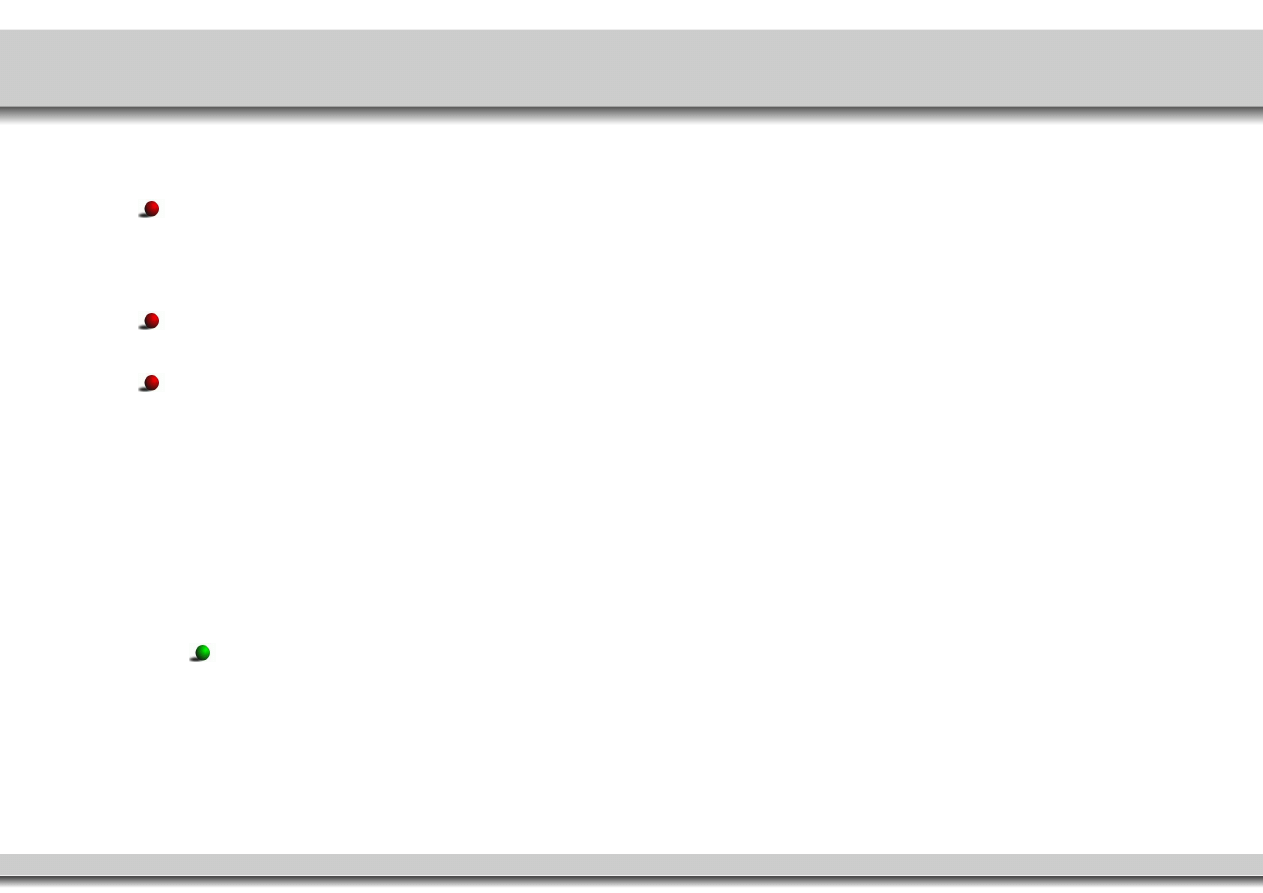
wtt gdy

n

1

< n

2

dr Anna M. Radzikowska, AiSD, wykład 6

– p.22/28

Metoda 4

W tej metodzie wykorzystujemy struktur˛e kopca z odwróconym

porz ˛

adkiem — teraz element minimalny jest w korzeniu.

Celem jest uzyskanie mo˙zliwie najdłu˙zszych bloków pocz ˛

atkowych.

Z ka˙zdym elementem kopca zwi ˛

azany jest dodatkowy atrybut nr b˛ed ˛

acy

numerem bloku odpowiadaj ˛

acemu temu elementowi. Teraz relacja

porz ˛

adku < ma posta´c:

Niech E

1

= (e

1

, n

1

) i E

2

= (e

2

, n

2

) b˛ed ˛

a dwoma elementami. E

1

< E

2

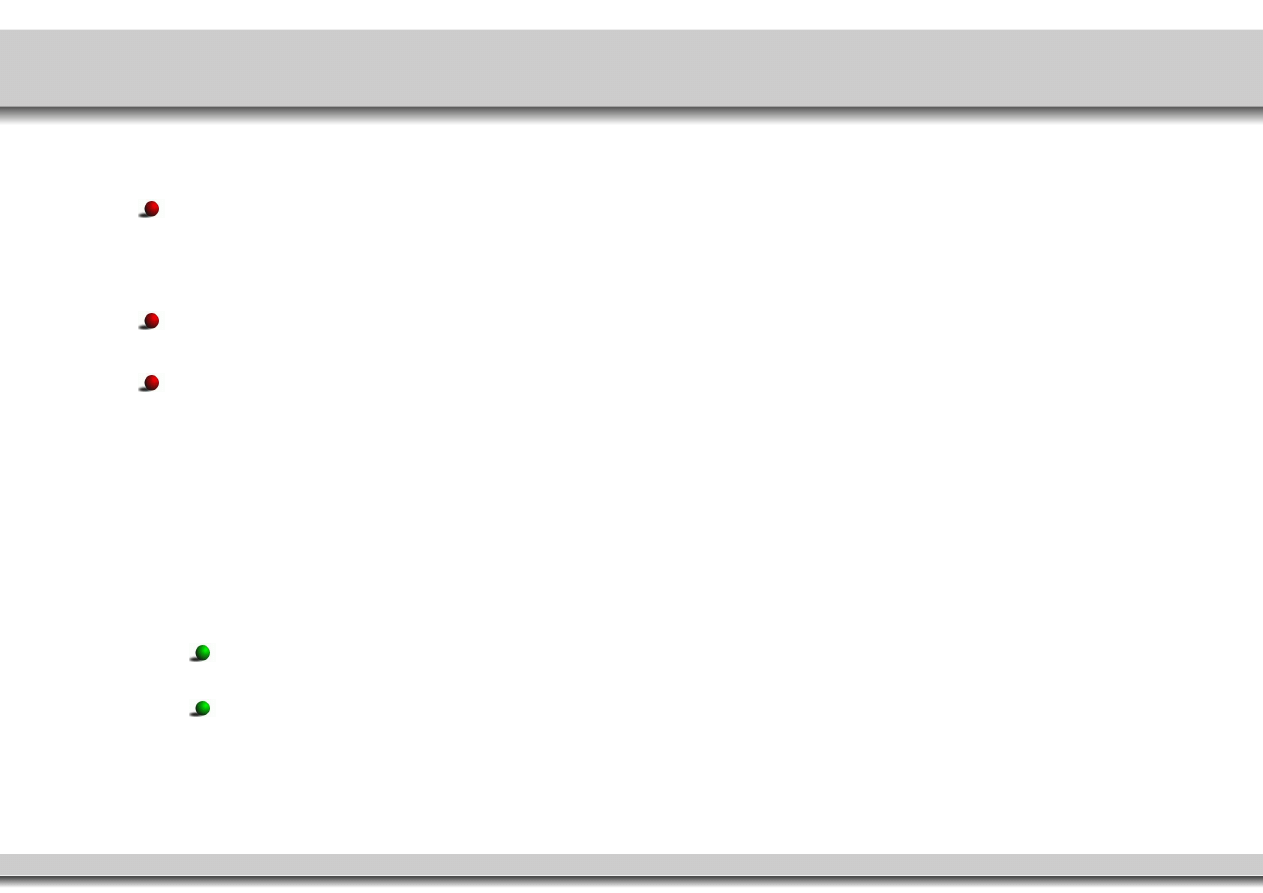
wtt gdy

n

1

< n

2

je´sli n

1

= n

2

, to e

1

< e

2

.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.22/28

Metoda 4 — ogólna idea

(i)

Wczytujemy z pliku p

0

m elementów i z nich budujemy kopiec.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.23/28

Metoda 4 — ogólna idea

(i)

Wczytujemy z pliku p

0

m elementów i z nich budujemy kopiec.

(ii)

Wypisujemy element z korzenia na plik p

i

i na jego miejsce wczytujemy

kolejny element x z pliku danych (o ile p

0

nie jest pusty; wpp wypisujemy

w porz ˛

adku rosn ˛

acym pozostałe elementy kopca).

dr Anna M. Radzikowska, AiSD, wykład 6

– p.23/28

Metoda 4 — ogólna idea

(i)

Wczytujemy z pliku p

0

m elementów i z nich budujemy kopiec.

(ii)

Wypisujemy element z korzenia na plik p

i

i na jego miejsce wczytujemy

kolejny element x z pliku danych (o ile p

0

nie jest pusty; wpp wypisujemy

w porz ˛

adku rosn ˛

acym pozostałe elementy kopca).

Je´sli x jest wi˛ekszy od elementu wypisanego, to z x

zwi ˛

azujemy bie˙z ˛

acy numer bloku

dr Anna M. Radzikowska, AiSD, wykład 6

– p.23/28

Metoda 4 — ogólna idea

(i)

Wczytujemy z pliku p

0

m elementów i z nich budujemy kopiec.

(ii)

Wypisujemy element z korzenia na plik p

i

i na jego miejsce wczytujemy

kolejny element x z pliku danych (o ile p

0

nie jest pusty; wpp wypisujemy

w porz ˛

adku rosn ˛

acym pozostałe elementy kopca).

Je´sli x jest wi˛ekszy od elementu wypisanego, to z x

zwi ˛

azujemy bie˙z ˛

acy numer bloku

Je´sli x jest mniejszy od elementu wypisanego, to z x

zwi ˛

azujemy numer nast˛epnego bloku.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.23/28

Metoda 4 — ogólna idea

(i)

Wczytujemy z pliku p

0

m elementów i z nich budujemy kopiec.

(ii)

Wypisujemy element z korzenia na plik p

i

i na jego miejsce wczytujemy

kolejny element x z pliku danych (o ile p

0

nie jest pusty; wpp wypisujemy

w porz ˛

adku rosn ˛

acym pozostałe elementy kopca).

Je´sli x jest wi˛ekszy od elementu wypisanego, to z x

zwi ˛

azujemy bie˙z ˛

acy numer bloku

Je´sli x jest mniejszy od elementu wypisanego, to z x

zwi ˛

azujemy numer nast˛epnego bloku.

Je´sli wszystkie elementy kopca maj ˛

a ten sam numer bloku,

to zwi˛ekszamy numer aktualnego boku i zapisujemy nowy

blok na nast˛epny plik pomocniczy.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.23/28

Metoda 4 — ogólna idea

(i)

Wczytujemy z pliku p

0

m elementów i z nich budujemy kopiec.

(ii)

Wypisujemy element z korzenia na plik p

i

i na jego miejsce wczytujemy

kolejny element x z pliku danych (o ile p

0

nie jest pusty; wpp wypisujemy

w porz ˛

adku rosn ˛

acym pozostałe elementy kopca).

Je´sli x jest wi˛ekszy od elementu wypisanego, to z x

zwi ˛

azujemy bie˙z ˛

acy numer bloku

Je´sli x jest mniejszy od elementu wypisanego, to z x

zwi ˛

azujemy numer nast˛epnego bloku.

Je´sli wszystkie elementy kopca maj ˛

a ten sam numer bloku,

to zwi˛ekszamy numer aktualnego boku i zapisujemy nowy

blok na nast˛epny plik pomocniczy.

(iii)

Poprawimy struktur˛e kopca i wracamy do

(ii)

.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.23/28

Tworzenie bloków pocz ˛

atkowych

1

proc ReplacementSort(var p

0

: plik);

2

var A : array

[1..m] of U ;

{reprezentacja kopca}

3

N : array

[1..m] of U ;

{numery bloków elementów kopca}

4

p : array

[1..k] of plik;

{tablica plików pomocniczych}

5

last

: U ;

{ostatnio wypisany element}

6

i, nb, np, l : integer;

7

begin

8

BuildHeap

(m);

9

np

:= 1

{aktualny plik pomocniczy}

10

for i

:= 1 to m do N

i

:= 1; od;

11

nb

:= 1;

{number aktualnego bloku}

12

l

:= m;

{ilo´s´c elementów kopca o aktualnym nr bloku}

13

write(p

np

, A

1

);

dr Anna M. Radzikowska, AiSD, wykład 6

– p.24/28

Tworzenie bloków pocz ˛

atkowych (cd.)

14

while

¬eof (p

0

) do

15

last

:= A

1

;

16

read(p

0

,A

1

);

17

if A

1

< last then

18

N

1

:= nb + 1;

19

l

:= l − 1;

20

if l

= 0 then

21

l

:= m; nb := nb + 1; np := (np mod k) + 1; fi;

22

fi;

23

Heapify_2

;

{poprawianie struktury kopca}

24

write(p

np

,A

1

);

25

od;

26

WriteHeap

;

27

end ReplacementSort;

dr Anna M. Radzikowska, AiSD, wykład 6

– p.25/28

Poprawianie struktury kopca

1

proc Heapify_2;

2

var i, k, nb : int; x : U ;

3

begin

4

i

:= 1; k := 2; x := A

1

; nb

:= N

1

;

5

while k

≤ m do

6

if k

+ 1 ≤ m then

7

if

(A

k+1

, N

k+1

) < (A

k

, N

k

)

8

then k

:= k + 1 fi fi;

9

if

(A

k

, N

k

) < (x, nb)

10

then A

i

:= A

k

; N

i

:= N

k

; i

:= k; k = 2k; fi;

11

od;

12

A

i

:= x; N

i

:= nb;

13

end Heapify_2;

dr Anna M. Radzikowska, AiSD, wykład 6

– p.26/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (40, 25, 60, 20, 10, 80, 35, 20, 75, 15, 5, 85, 30, 50, 65, 45, 20, 30)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

40

,

25

,

60

,

20

,

10, 80, 35, 20, 75, 15, 5, 85, 30, 50, 65, 45, 20, 30)

Kopiec:

{40|1 , 25|1 , 60|1 ,

20|1

}

nb

= 1

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

10

,

80, 35, 20, 75, 15, 5, 85, 30, 50, 65, 45, 20, 30)

Kopiec:

{40|1 ,

25|1

,

60|1 ,

10|2

}

nb

= 1

p

1

: (20)

p

2

: ()

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

80

,

35, 20, 75, 15, 5, 85, 30, 50, 65, 45, 20, 30)

Kopiec:

{

40|1

,

80|1

,

60|1 , 10|2}

nb

= 1

p

1

: (20, 25)

p

2

: ()

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

35

,

20, 75, 15, 5, 85, 30, 50, 65, 45, 20, 30)

Kopiec:

{

35|2

,

80|1 ,

60|1

,

10|2}

nb

= 1

p

1

: (20, 25, 40)

p

2

: ()

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

20

,

75, 15, 5, 85, 30, 50, 65, 45, 20, 30)

Kopiec:

{35|2 ,

80|1

,

20|2

,

10|2}

nb

= 1

p

1

: (20, 25, 40, 60)

p

2

: ()

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

75

,

15, 5, 85, 30, 50, 65, 45, 20, 30)

Kopiec:

{35|2 ,

75|2

,

20|2 ,

10|2

}

nb

= 2

p

1

: (20, 25, 40, 60, 80)

p

2

: ()

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

15

,

5, 85, 30, 50, 65, 45, 20, 30)

Kopiec:

{35|2 , 75|2 , 20|2 ,

15|2

}

nb

= 2

p

1

: (20, 25, 40, 60, 80)

p

2

: (10)

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

5

,

85, 30, 50, 65, 45, 20, 30)

Kopiec:

{35|2 , 75|2 ,

20|2

,

5|3

}

nb

= 2

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15)

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

85

,

30, 50, 65, 45, 20, 30)

Kopiec:

{

35|2

,

75|2 ,

85|2

,

5|3}

nb

= 2

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20)

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

30

,

50, 65, 45, 20, 30)

Kopiec:

{

30|3

,

75|2

,

85|2 , 5|3}

nb

= 2

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35)

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

50

,

65, 45, 20, 30)

Kopiec:

{30|3 ,

50|3

,

85|2

,

5|3}

nb

= 2

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75)

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

65

,

45, 20, 30)

Kopiec:

{30|3 , 50|3 ,

65|3

,

5|3

}

nb

= 3

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: ()

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

45

,

20, 30)

Kopiec:

{

30|3

,

50|3 , 65|3 ,

45|3

}

nb

= 3

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: (5)

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

20

,

30)

Kopiec:

{

20|4

,

50|3 , 65|3 ,

45|3

}

nb

= 3

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: (5, 30)

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= (

30

)

Kopiec:

{20|4 ,

50|3

,

65|3 ,

30|4

}

nb

= 3

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: (5, 30, 45)

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= ()

Kopiec:

{20|4 ,

65|3

,

30|4}

nb

= 3

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: (5, 30, 45, 50)

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= ()

Kopiec:

{

20|4

,

30|4}

nb

= 4

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: (5, 30, 45, 50, 65)

p

4

: ()

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= ()

Kopiec:

{

30|4

}

nb

= 4

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: (5, 30, 45, 50, 65)

p

4

: (20)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Metoda 4 — przykład

Przykład 6.5

m

= k = 4

p

0

= ()

Kopiec:

∅

nb

= 4

p

1

: (20, 25, 40, 60, 80)

p

2

: (10, 15, 20, 35, 75, 85)

p

3

: (5, 30, 45, 50, 65)

p

4

: (20, 30)

dr Anna M. Radzikowska, AiSD, wykład 6

– p.27/28

Dzi˛ekuj˛e za uwag˛e!

Pytania bardzo mile widziane.

dr Anna M. Radzikowska, AiSD, wykład 6

– p.28/28