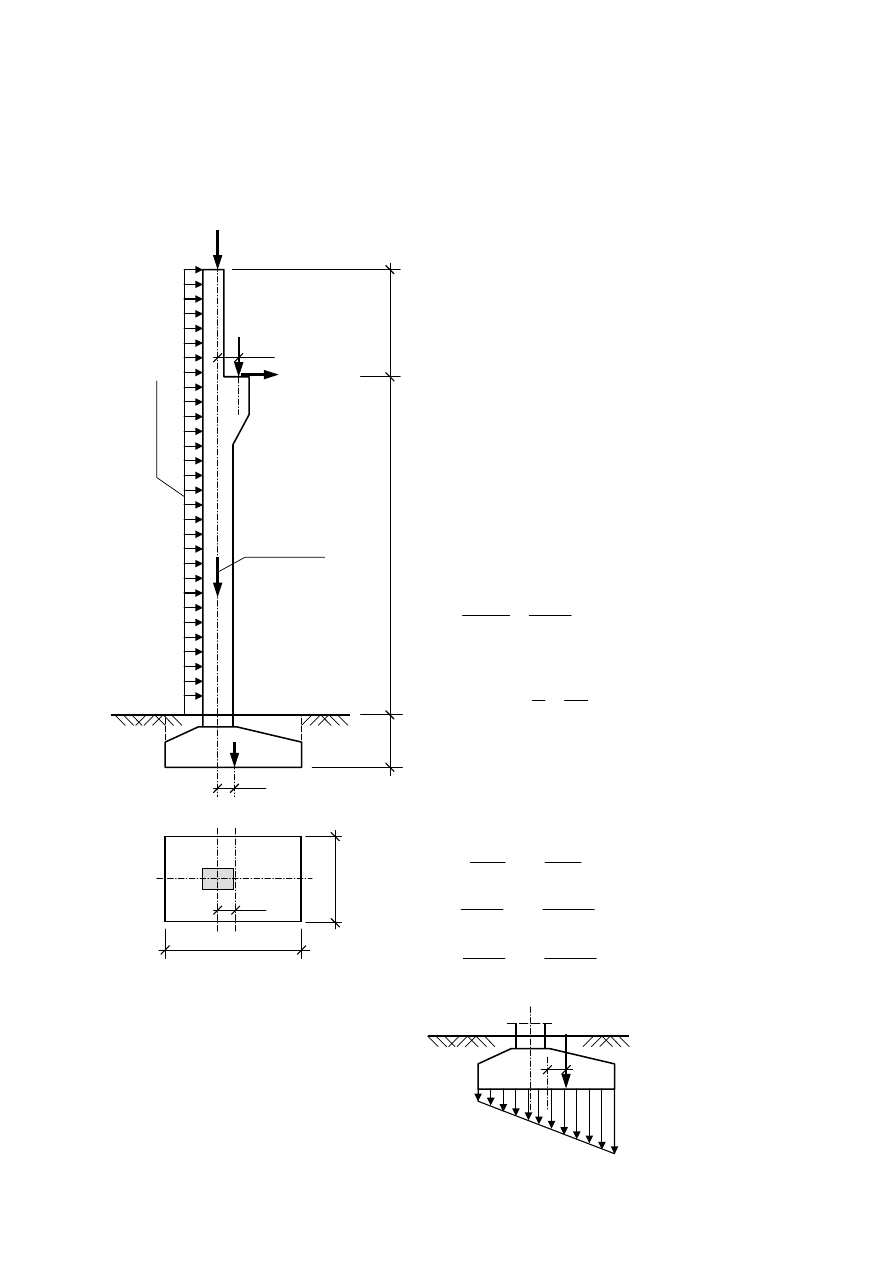
1
Fundamentowanie – ćwiczenia
Część 1 – Naciski na grunt pod fundamentami bezpośrednimi
(dr inż. Adam Krasiński, mgr inż. Tomasz Kusio)
Zadanie przykładowe 1.1
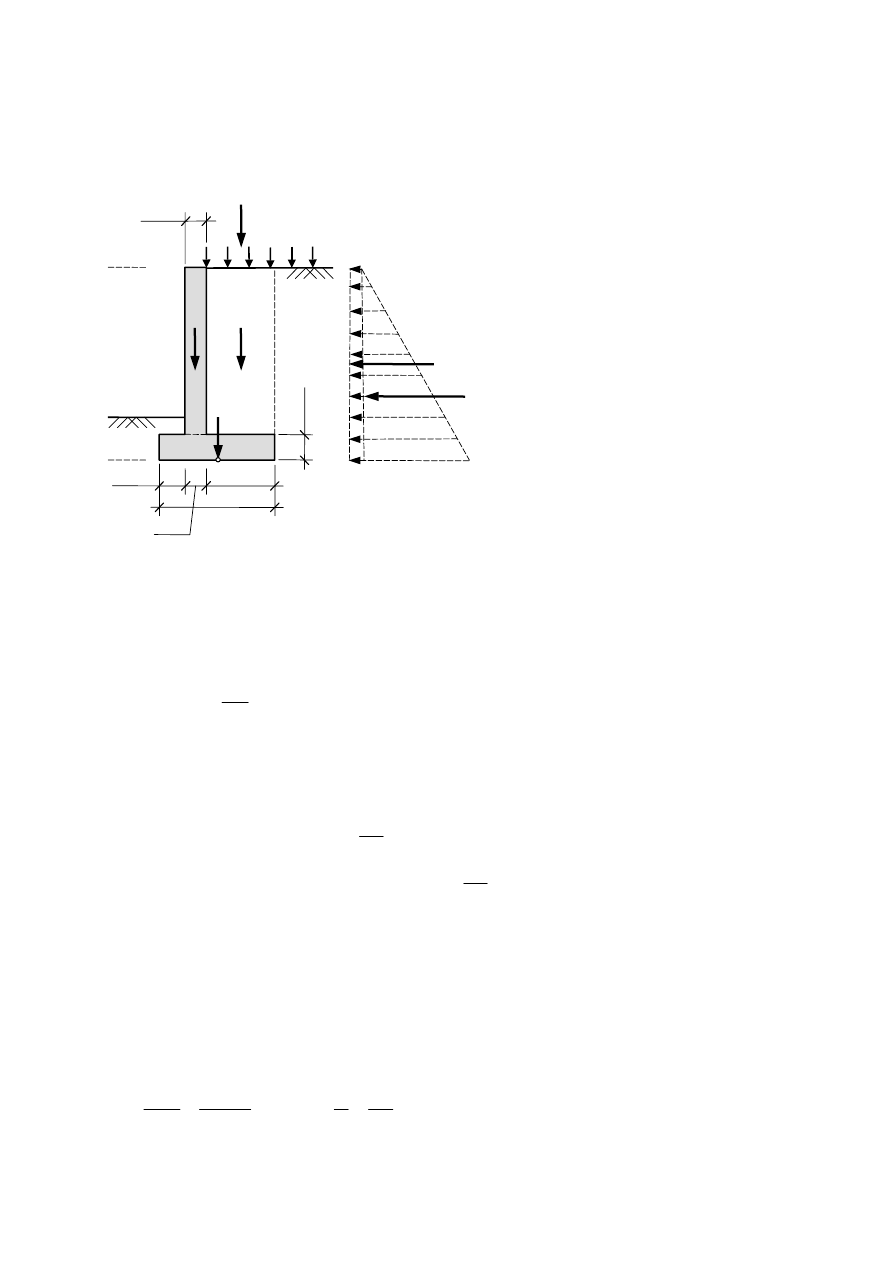
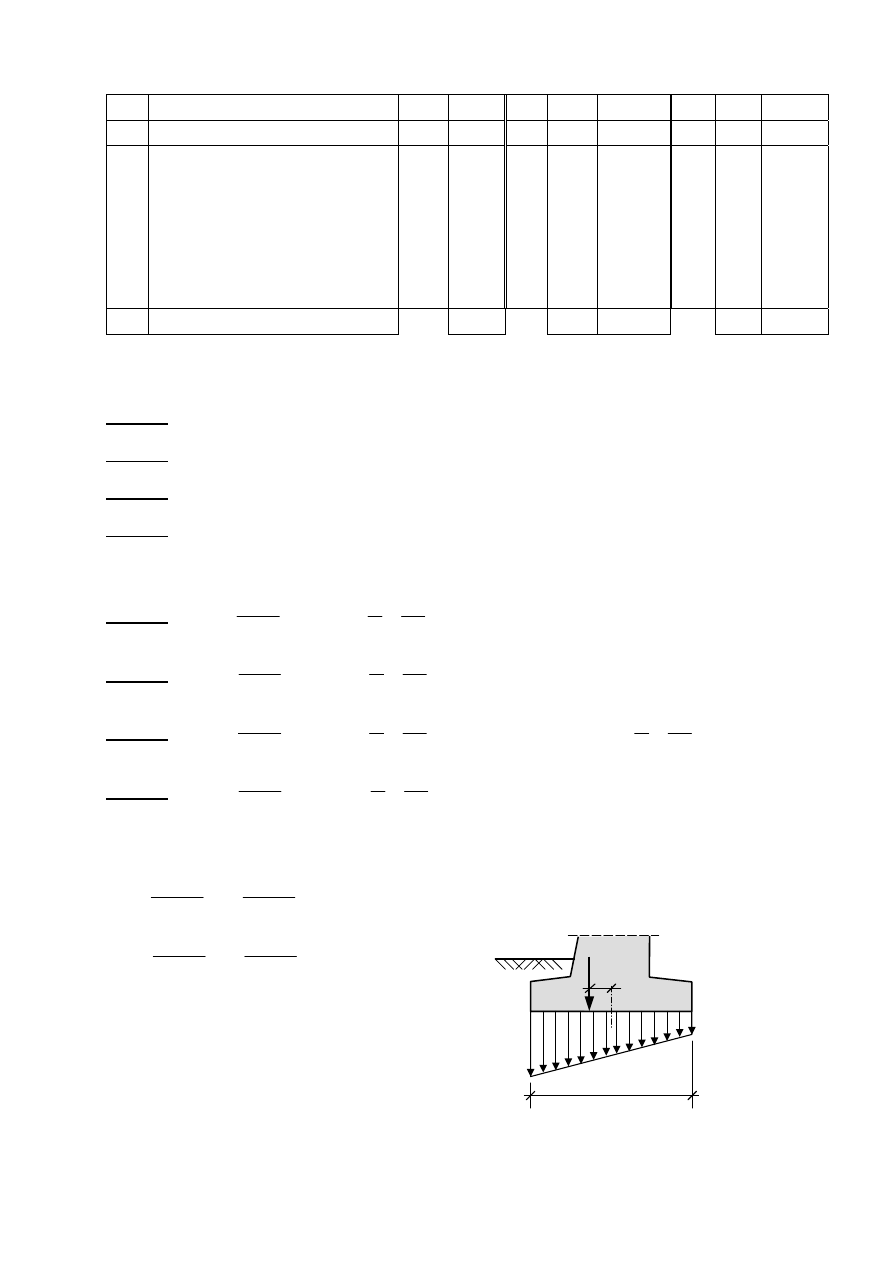
Wyznaczyć naciski na grunt pod stopą fundamentową słupa hali przemysłowej.
Obliczenia
Przyjęto uśredniony ciężar objętościowy betonu
i gruntu:
γ
śr
= 22,0 kN/m
3
Ciężar stopy fundamentowej z obsypką gruntową:
G
F
= 3,2
⋅2,0⋅1,20⋅22,0 = 169,0 kN
Suma obciążeń pionowych:
ΣV = 150,0 + 300,0 + 45,0 + 169,0 = 664,0 kN
Suma momentów względem środka podstawy
fundamentu:
ΣM
0
= 150,0
⋅(-0,40) + 45⋅(-0,40) + 300⋅(0,50-0,40) +
+ 15,0
⋅(8,0+1,2) + 3,0⋅(8,0 + 2,5)⋅(0,5⋅(8,0 +2,5) +
1,2) = 293,2 kNm
Mimośród wypadkowej obciążeń:
44
,
0
0
,
664
2
,
293
0
=
=
=
∑
∑
V
M
e
L
m
Warunek dotyczący mimośrodu:
44
,
0
=
L
e
m <
53
,
0
6
2
,
3
6
=
=
L
m
Wypadkowa obciążeń znajduje się w rdzeniu podstawy
fundamentu.
Wartości nacisków na grunt:
4
,
6
0
,
2
2
,
3
=
⋅
=
F
m
2
)
6
1
(
2
,
1
L
e
F
V
q
L
⋅
±
⋅
=
∑
=
⋅
+
⋅
=
)
2
,
3
44
,
0
6
1
(
4
,
6
0
,
664
1
q
189,3 kPa
=
⋅
−
⋅
=
)
2
,
3
44
,
0
6
1
(
4
,
6
0
,
664
2
q
18,2 kPa
P
1
= 300 kN
P
2
= 150 kN
H
1
= 15 kN
0,5 m
G
s
= 45 kN
G
F
0,4 m
γ
śr
2,5 m
8,0 m
1,2 m
0
B
= 2,0 m
0,4 m
L = 3.2 m
Rzut fundamentu
q
w
= 3,0 kN/m
1
2
1
1
2
2
0
q
1
q
2
e
L
Σ
V
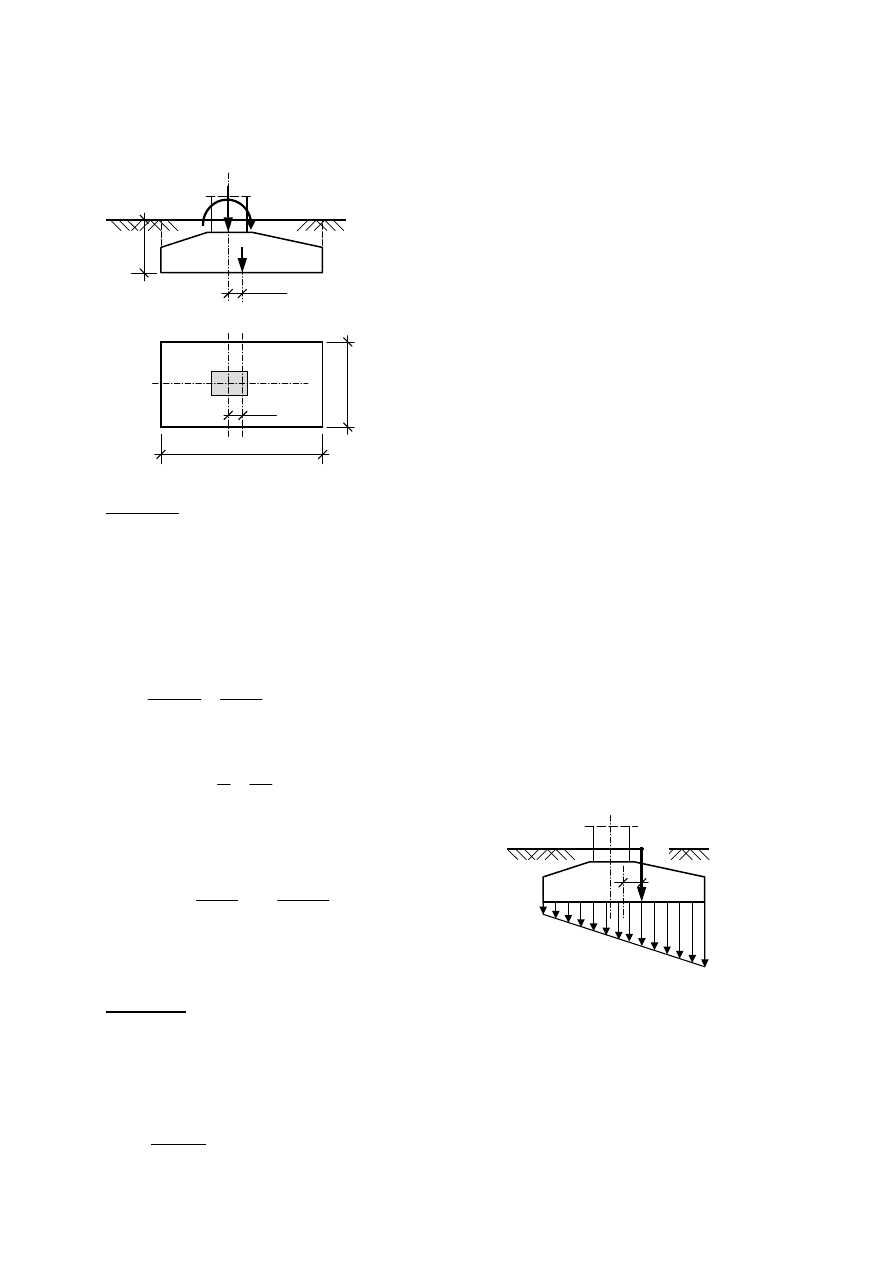
2
Zadanie przykładowe 1.2
Wyznaczyć i sprawdzić rozkłady nacisków na grunt pod stopą fundamentową słupa dla dwóch
wariantów obciążeń przekazywanych przez słup.
Obciążenia ze słupa:
Wariant I : V
I
= 700 kN, M
I
= 650 kNm
Wariant II : V
II
= 350 kN, M
II
= -300 kNm
Obliczenia
Podobnie jak w zad. 1.1, przyjęto uśredniony ciężar
objętościowy betonu i gruntu:
γ
śr
= 22,0 kN/m
3
Ciężar stopy fundamentowej z obsypką gruntową:
G
F
= 3,8
⋅2,0⋅1,20⋅22,0 = 200,6 kN
Powierzchnia podstawy fundamentu:
F = 3,8
⋅2,0 = 7,60 m
2
Wariant I
Suma obciążeń pionowych:
ΣV
I
= 700,0 + 200,6 = 900,6 kN
Suma momentów względem środka podstawy fundamentu:
ΣM
0I
= 650,0
⋅+ 700⋅(-0,35) = 405,0 kNm
Mimośród wypadkowej obciążeń:
45
,
0
6
,
900
0
,
405
0
=
=
=
∑
∑
I
I
LI
V
M
e
m
Warunek dotyczący mimośrodu:
45
,
0
=
LI
e
m <
63
,
0
6
8
,
3
6
=
=
L
m
→
wypadkowa obciążeń znajduje się w rdzeniu podstawy fundamentu.
Wartości nacisków na grunt:
F = 3,8
⋅2,0 = 7,60 m
2
=
⋅
+
⋅
=
=
)
8
,
3
45
,
0
6
1
(
6
,
7
6
,
900
1
max
q
q
I
202,7
kPa
Wariant II
ΣV
II
= 350,0 + 200,6 = 550,6 kN
ΣM
0II
= -300,0
⋅+ 350⋅(-0,35) = -422,5 kNm
Mimośród wypadkowej obciążeń:
77
,
0
6
,
550
5
,
422
−
=
−
=
LII
e
m
G
F
0,35 m
γ
śr
0
B
= 2,0 m
0,35 m
L = 3.8 m
Rzut fundamentu
1
1
2
2
1,2 m
V
M
0
0
q
1
= q
maxI
=
= 202,7 kPa
e
LI
Σ
V
I
1
2
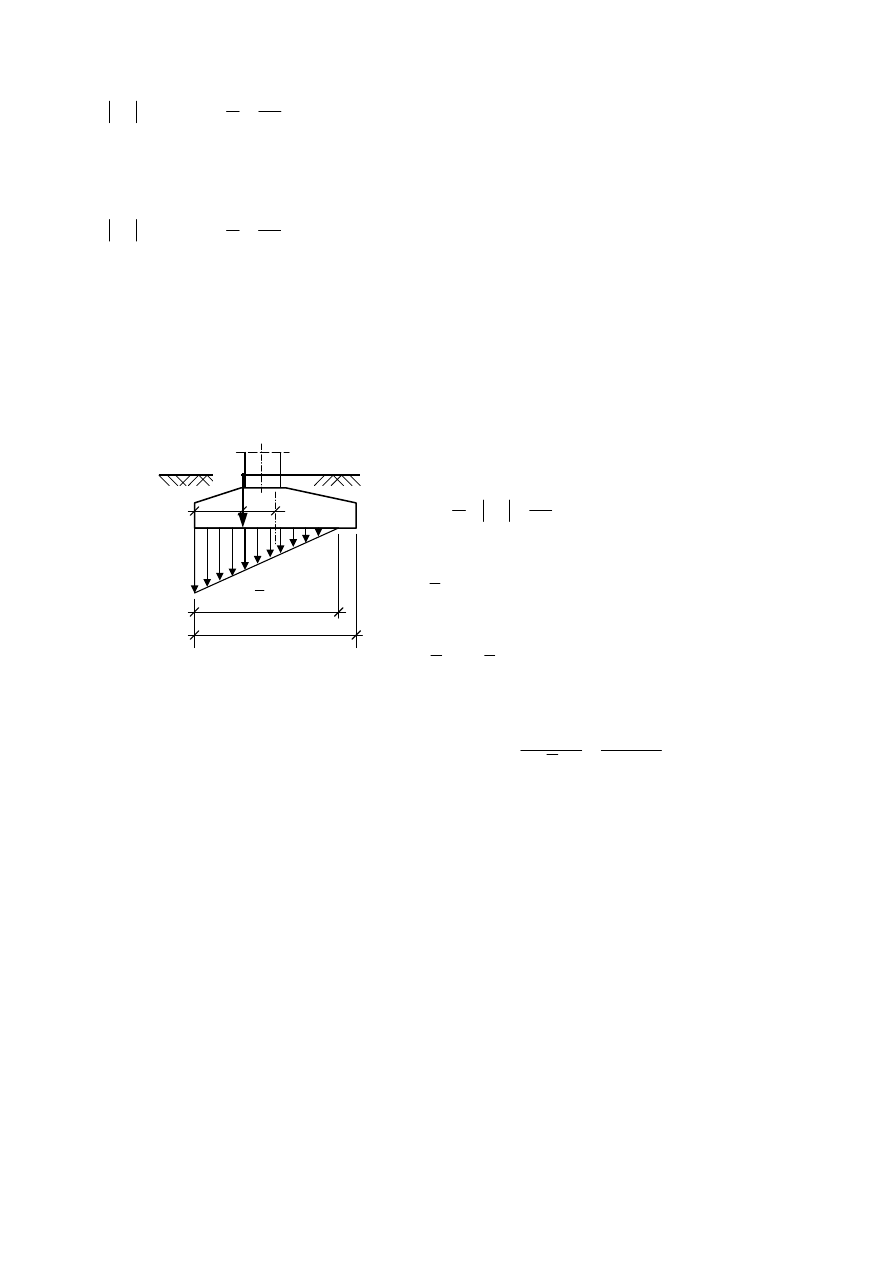
3
Warunek dotyczący mimośrodu:
77
,
0
=
LII
e
m >
63
,
0
6
8
,
3
6
=
=
L
m
→
wypadkowa obciążeń znajduje się poza rdzeniem podstawy fund.
Przepisy normowe dopuszczają nieznaczne przekroczenie warunku mimośrodu dla najniekorzyst-
niejszych wariantów obciążeń obliczeniowych, jednak nie więcej niż L/4 (lub B/4).
77
,
0
=
LII
e
m <
95
,
0
4
8
,
3
4
=
=
L
m
→ mimośród spełnia przepisy normowe
Wartości nacisków na grunt:
W przypadku, gdy wypadkowa obciążeń wychodzi poza rdzeń podstawy fundamentu, obliczanie
nacisków na grunt należy wykonywać według innej procedury niż w wariancie I. Wynika to z faktu,
że grunt nie przenosi rozciągania (na styku fundament-grunt nie może być naprężeń rozciąga-
jących).
Długość odcinka l:
13
,
1
77
,
0
2
8
,
3
2
=
−
=
−
=
LII
e
L
l
m
Efektywna długość fundamentu:
39
,
3
13
,
1
3
3
=
⋅
=
⋅
= l
L
m
Efektywna powierzchnia fundamentu:
78
,
6
39
,
3
0
,
2
=
⋅
=
⋅
=
L
B
F
m
2
Wartości nacisków na grunt:
=
⋅
=
⋅
=
=
∑
78
,
6
6
,
550
2
2
2
max
F
V
q
q
II
II
162,2 kPa
Większe wartości nacisków na grunt otrzymano dla wariantu I obciążeń.
0
q
2
= q
maxII
e
LII
Σ
V
II
1
2
l
L
L
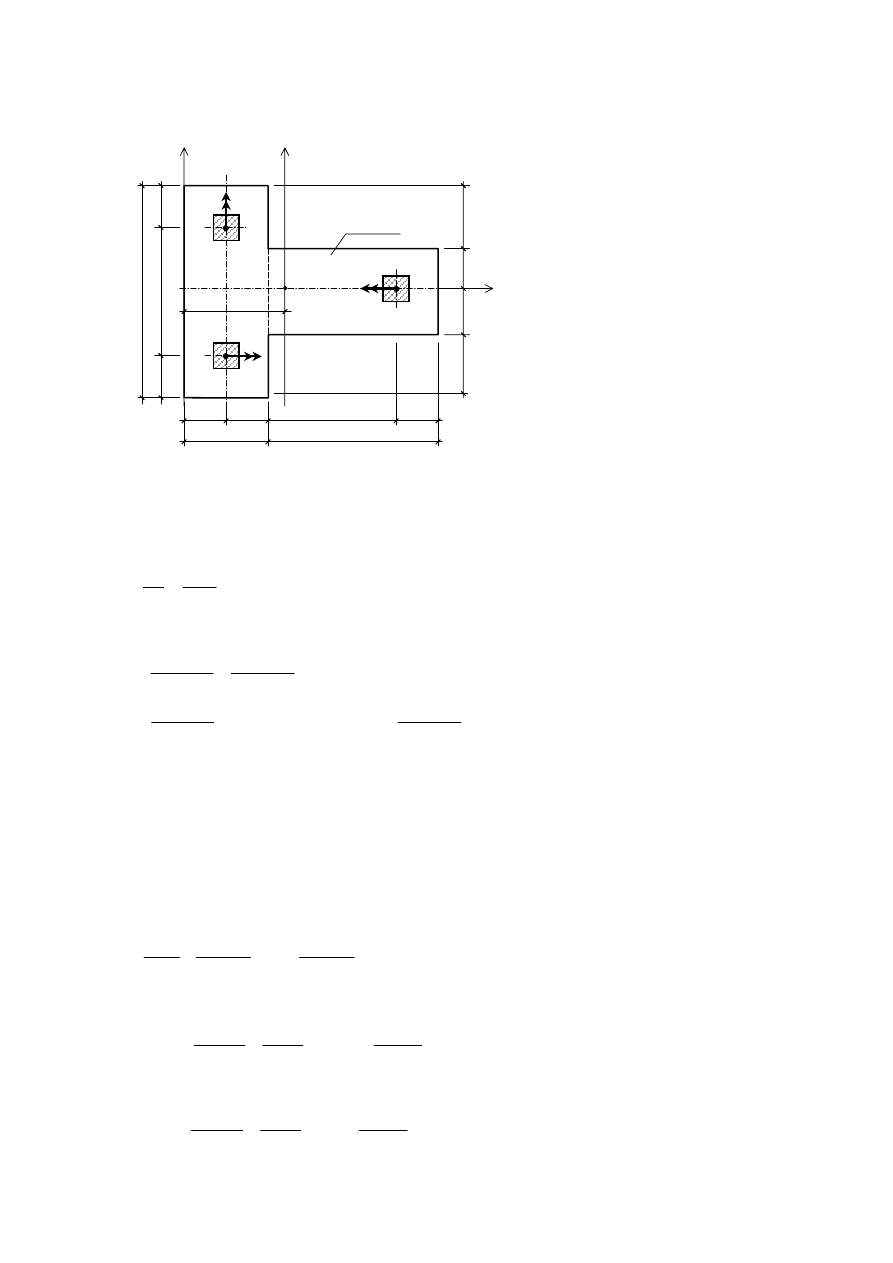
4
Zadanie przykładowe 1.3
Policzyć wartości maksymalnych i minimalnych nacisków na grunt pod fundamentem
bezpośrednim przedstawionym na rysunku poniżej.
Obciążenia ze słupów:
V
1
= 500 kN, M
1
= 1000 kNm
V
2
= 800 kN, M
2
= 1200 kNm
V
3
= 1000 kN, M
3
= 1500 kNm
Ciężar objętościowy żelbetu:
γ
b
= 25,0 kN/m
3
Obliczenia
Wyznaczenie położenia środka geometrycznego podstawy fundamentu:
F = 2,0
⋅5,0 + 2,0⋅4,0 = 18,0 m
2
S
Y
= 2,0
⋅5,0⋅1,0 + 2,0⋅4,0⋅4,0 = 42,0 m
3
33
,
2
0
,
18
0
,
42
0
=
=
=
F
S
x
Y
m
Momenty bezwładności podstawy fundamentu:
5
,
23
12
0
,
2
0
,
4
12
0
,
5
0
,
2
3
3
0
=
⋅
+
⋅
=
x
J
m
4
0
,
54
)
33
,
2
0
,
4
(
0
,
4
0
,
2
12
0
,
4
0
,
2
)
0
,
1
33
,
2
(
0
,
2
0
,
5
12
0
,
2
0
,
5
2
3
2
3
0
=
−
⋅
⋅
+
⋅
+
−
⋅
⋅
+
⋅
=
y
J
m
4
Sprowadzenie obciążeń do środka geometrycznego fundamentu:
Ciężar fundamentu: G
F
= 18,0
⋅0,80⋅25,0 = 360,0 kN
0
,
2660
0
,
360
0
,
1000
0
,
800
0
,
500
=
+
+
+
=
∑
V
kN
0
,
150
5
,
1
0
,
800
5
,
1
0
,
500
0
,
1500
0
,
1200
0
=
⋅
+
⋅
−
−
=
∑
x
M
kNm
0
,
1941
)
33
,
2
0
,
5
(
0
,
1000
)
0
,
1
33
,
2
(
0
,
800
)
0
,
1
33
,
2
(
0
,
500
0
,
1000
0
=
−
⋅
+
−
⋅
−
−
⋅
−
=
∑
y
M
kNm
Obliczenie nacisków na grunt pod podstawą fundamentu:
j
y
y
j
x
x
j
x
J
M
y
J
M
F
V
q
0
0
0
0
0
0
⋅
+
⋅
−
=
∑
∑
∑
Maksymalne naciski występują pod narożnikiem F
=
⋅
+
−
⋅
−
=
=
67
,
3
0
,
54
0
,
1941
)
0
,
1
(
5
,
23
0
,
150
0
,
18
0
,
2660
max
F
q
q
286,1
kPa
Minimalne naciski występują pod narożnikiem A
=
−
⋅
+
⋅
−
=
=
)
33
,
2
(
0
,
54
0
,
1941
50
,
2
5
,
23
0
,
150
0
,
18
0
,
2660
min
A
q
q
48,1
kPa
Minimalne naciski dodatnie
→ wypadkowa obciążeń zawiera się w rdzeniu podstawy fundamentu.
1,0m
1,0m
0
3,0m
1,0m
5,0m
1,0m 3,0m 1,0m
2,0m 4,0m
1,5m
1,0m
1,0m
1,5m
g = 0,8m
Y Y
0
X
0
x
0
M
1
M
3
M
2
V
1
V
2
V
3
A B
E
C D
F
5
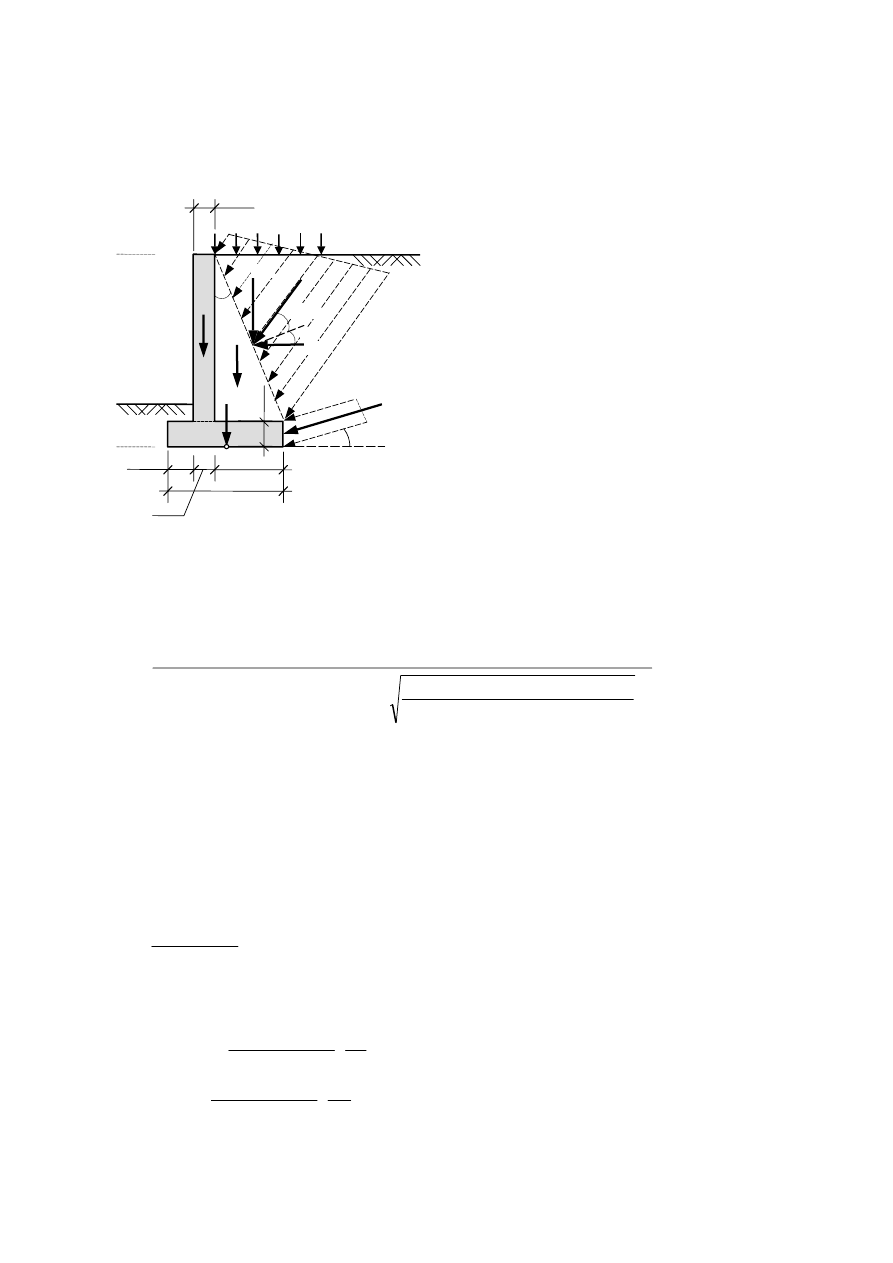
Zadanie przykładowe 1.4
Zebrać obciążenia i sprawdzić położenie wypadkowej obciążeń w podstawie fundamentu ściany
oporowej, pokazanej na rysunku poniżej. Przyjąć: parcie graniczne gruntu, ciężar betonu
γ
b
=25
kN/m
3
oraz uproszczony sposób zbierania obciążeń.
Obliczenia
Wypadkowe obciążeń pionowych oraz ich
położenie względem punktu „0”:
Ciężar płyty fundamentowej:
50
,
40
0
,
25
6
,
0
7
,
2
1
=
⋅
⋅
=
G
kN/m,
0
01
=
r
Ciężar ściany:
75
,
48
0
,
25
5
,
0
9
,
3
2
=
⋅
⋅
=
G
kN/m,
5
,
0
02
=
r
m
Ciężar gruntu spoczywającego na odsadzce
fundamentu:
32
,
112
0
,
18
9
,
3
6
,
1
3
=
⋅
⋅
=
G
kN/m,
55
,
0
03
−
=
r
m
Obciążenie naziomu:
0
,
16
0
,
10
6
,
1
=
⋅
=
P
kN/m,
55
,
0
0
−
=
P
r
m
Suma sił oraz momentów względem punktu „0” od oddziaływań pionowych:
57
,
217
0
,
16
32
,
112
75
,
48
5
,
40
=
+
+
+
=
ΣV
kN/m
2
,
46
55
,
0
0
,
16
5
,
0
32
,
112
5
,
0
75
,
48
)
(
0
−
=
⋅
−
⋅
−
⋅
=
Σ
V
M
kNm/m
Obciążenia poziome – parcie gruntu
307
,
0
2
32
45
2
=
°
−
°
= tg
K
a
07
,
3
307
,
0
0
,
10
1
=
⋅
=
a
e
kPa
(
)
94
,
27
307
,
0
0
,
18
50
,
4
0
,
10
2
=
⋅
⋅
+
=
a
e
kPa
Wypadkowe parcia gruntu:
82
,
13
07
,
3
5
,
4
1
=
⋅
=
E
kN/m,
25
,
2
2
5
,
4
1
0
=
=
E
r
m
(
)
96
,
55
07
,
3
94
,
27
5
,
4
5
,
0
2
=
−
⋅
⋅
=
E
kN/m,
5
,
1
3
5
,
4
2
0
=
=
E
r
m
Suma sił i momentów względem punktu „0” od oddziaływań poziomych:
78
,
69
96
,
55
82
,
13
2
1
=
+
=
+
=
Σ
E
E
H
kN/m
04
,
115
5
,
1
96
,
55
25
,
2
82
,
13
)
(
0
=
⋅
+
⋅
=
Σ
H
M
kNm/m
Suma momentów względem punktu „0” od wypadkowych obciążeń pionowych i poziomych:
02
,
69
02
,
46
04
,
115
0
=
−
=
ΣM
kNm/m
Wartość mimośrodu i sprawdzenie warunku dotyczącego mimośrodu:
32
,
0
57
,
217
02
,
69
0
=
=
Σ
Σ
=
V
M
e
B
m
45
,
0
6
7
,
2
6
=
=
<
B
m
Warunek spełniony - wypadkowa obciążeń zawiera się w rdzeniu podstawy.
+3,50 m
±0,00 m
-1,00 m
0,6 m
0,5 m
1,6 m
2,7 m
0,
6 m
0,5 m
P
p=10 kN/m
2
e
a1
e
a2
E
1
E
2
G
2
G
3
G
1
0
FSa
φ
=32
o
γ
=18 kN/m
3
6
Zadanie przykładowe 1.4a
Wykonać ponownie obliczenia z przykładu 1.4, przyjmując bardziej zaawansowany schemat
zbierania obciążeń.
Obliczenia
Wypadkowe obciążeń pionowych oraz ich
położenie względem punktu „0”:
Ciężar płyty fundamentowej:
G
1
40,50
25,0
0,6
2,7
=
⋅
⋅
=
kN/m,
0
01
=
r
Ciężar własny ściany:
G
2
48,75
25,0
0,5
3,9
=
⋅
⋅
=
kN/m,
5
,
0
02
=
r
m
Ciężar gruntu spoczywającego na odsadzce
fundamentu:
G
3
,16
6
5
,0
8
1
9
,
3
6
,
1
5
,
0
=
⋅
⋅
⋅
=
kN/m,
28
,
0
6
,
1
67
,
0
35
,
1
03
−
=
⋅
+
−
=
r
m
Wartości oraz położenie składowych pionowych i poziomych parcia gruntu względem punktu „0”:
Współczynnik parcia gruntu na powierzchnię ukośną bloku gruntowego za ścianą oporową:
tg
β
= 1,6 / 3,9 = 0,41 →
β
= 22,3°;
δ
a1
=
φ
= 32° (tarcie gruntu o grunt),
ε
= 0
(
)
(
)
(
)
(
)
(
)
(
)
517
,
0
0
3
,
22
cos
32
3
,
22
cos
0
32
sin
32
32
sin
1
32
3
,
22
cos
3
,
22
cos
32
3
,
22
cos
2
2
2
1
=
°
−
°
⋅
°
+
°
°
−
°
⋅
°
+
°
+
⋅
°
+
°
⋅
°
°
−
°
=
a
K
Współczynnik parcia gruntu na pionową ścianę fundamentu:
β
= 0°;
δ
a2
=
φ
/2 = 16° (gładka powierzchnia betonowa)
278
,
0
2
=
a
K
(obliczone według wzoru jak wyżej)
Wartości parcia gruntu na powierzchnię ukośną bloku gruntowego oraz ich położenie
wypadkowych względem punktu „0”:
17
,
5
517
,
0
0
,
10
1
=
⋅
=
a
e
kPa
(
)
46
,
41
517
,
0
0
,
18
90
,
3
0
,
10
2
=
⋅
⋅
+
=
a
e
kPa
93
,
90
9
,
3
2
46
,
41
17
,
5
1
=
⋅
+
=
a
E
kN/m
(
)
(
)
84
,
73
32
3
,
22
sin
93
,
90
sin
1
1
1
=
°
+
°
⋅
=
+
⋅
=
a
a
v
a
E
E
δ
β
kN/m
(
)
(
)
06
,
53
32
3
,
22
cos
93
,
90
cos
1
1
1
=
°
+
°
⋅
=
+
⋅
=
a
a
h
a
E
E
δ
β
kN/m
( )
76
,
0
59
,
0
35
,
1
3
6
,
1
46
,
41
17
,
5
46
,
41
17
,
5
2
35
,
1
1
0
−
=
+
−
=
⋅
+
+
⋅
+
−
=
v
a
E
r
m
( )
04
,
2
44
,
1
6
,
0
3
9
,
3
46
,
41
17
,
5
46
,
41
17
,
5
2
6
,
0
1
0
=
+
=
⋅
+
+
⋅
+
=
h
a
E
r
m
Wartości parcia gruntu na ścianę fundamentu oraz położenie wypadkowych względem punktu „0”:
(
)
30
,
22
278
,
0
0
,
18
9
,
3
0
,
10
3
=
⋅
⋅
+
=
a
e
kPa
+3,50 m
±0,00 m
-1,00 m
0,6 m
0,5 m
1,6 m
2,7 m
0,
6 m
0,5 m
p=10 kN/m
2
e
a1
e
a2
E
a1
E
a2
G
2
G
3
G
1
0
FSa
φ
=32
o
γ
=18 kN/m
3
β
δ
a1
=
φ
δ
a2
=
φ
/2=16°
e
a4
E
h
a1
E
v
a1
β
e
a3

7
(
)
30
,
25
278
,
0
0
,
18
5
,
4
0
,
10
4
=
⋅
⋅
+
=
a
e
kPa
28
,
14
6
,
0
2
30
,
25
30
,
22
2
=
⋅
+
=
a
E
kN/m
94
,
3
16
sin
28
,
14
sin
2
2
2
=
°
⋅
=
⋅
=
a
a
v
a
E
E
δ
kN/m,
( )
35
,
1
2
0
−
=
v
a
E
r
m
73
,
13
16
cos
28
,
14
cos
2
2
2
=
°
⋅
=
⋅
=
a
a
h
a
E
E
δ
kN/m,
( )
30
,
0
2
0
=
h
a
E
r
m
Suma obciążeń pionowych:
19
,
223
94
,
3
84
,
73
16
,
56
75
,
48
5
,
40
=
+
+
+
+
=
∑V
kN/m
Suma obciążeń poziomych:
79
,
66
73
,
13
06
,
53
=
+
=
∑ H
kN/m
Suma momentów względem punktu „0” od wypadkowych obciążeń pionowych i poziomych:
(
)
(
)
(
)
+
−
⋅
+
⋅
+
−
⋅
+
−
⋅
+
⋅
=
∑
35
,
1
94
,
3
04
,
2
06
,
53
76
,
0
84
,
73
28
,
0
16
,
56
5
,
0
75
,
48
0
M
57
,
59
3
,
0
73
,
13
=
⋅
+
kNm/m
Wartość mimośrodu i sprawdzenie warunku:
27
,
0
19
,
223
57
,
59
0
=
=
Σ
Σ
=
V
M
e
B
m
45
,
0
6
7
,
2
6
=
=
<
B
m
Wypadkowa obciążeń zawiera się w rdzeniu podstawy.
Wniosek: bardziej zaawansowana metoda zbierania obciążeń dała nieznacznie korzystniejszy wynik
(mniejszą wartość mimośrodu).
8
Zadanie przykładowe 1.5
Obliczyć i zebrać obciążenia działające na ścianę oporową ze wspornikiem oraz sprawdzić warunki
normowe dotyczące mimośrodu wypadkowej obciążeń w podstawie fundamentu ściany dla różnych
kombinacji obciążeń.
Zestawienie obciążeń pionowych na 1 mb ściany oporowej
Obc. Wartość charakt. V
k
r
0
M
0
(V
k
)
γ
F;max
V
d;max
M
0
(V
d;max
)
γ
F;min
V
d;min
M
0
(V
d;min
)
kN
m kNm kN kNm kN kNm
G
1
G
2
G
3
G
4
G
5
G
6
P
3,2
⋅0,6⋅24,0 = 46,1
0,5
⋅4,90⋅24,0 = 58,8
0,5
⋅1,0⋅4,90⋅24,0 = 58,8
0,5
⋅(0,3+0,6)⋅1,20⋅24,0 = 13,0
0,85
⋅2,80⋅17,5 = 41,7
1,20
⋅1,50⋅17,5 = 31,5
1,20
⋅14,0 = 16,8
0,0
-0,5
0,08
-1,35
-1,18
-1,35
-1,35
0,0
-29,4
4,7
-17,5
-49,1
-42,5
-22,7
1,35
1,35
1,35
1,35
1,35
1,35
1,5
62,2
79,4
79,4
17,6
56,3
42,5
21,6
0,0
-39,7
6,3
-23,6
-66,3
-57,4
-30,6
1,0
1,0
1,0
1,0
1,0
1,0
0,0
46,1
58,8
58,8
13,0
41,7
31,5
0,0
0,0
-29,4
4,7
-17,5
-49,1
-42,5
0,0
Σ
266,7
-156,5
359,0
-211,3
249,9
-133,8
Obciążenia poziome - parcie gruntu
Przyjęto parcie gruntu pośrednie ze współczynnikiem
2
0
a
I
K
K
K
+
=
Współczynnik parcia spoczynkowego – zastosowano wzór dla gruntu nasypowego, zagęszczanego
mechanicznie
Współczynniki:
ξ
4
= 0,07 (grunty niespoiste przemieszane)
ξ
5
= 0,90 (zagęszczanie metodą lekką wibracyjną)
Wskaźnik zagęszczenia (według wzoru Borowczyka i Frankowskiego):
96
,
0
60
,
0
188
,
0
845
,
0
188
,
0
845
,
0
=
⋅
+
=
⋅
+
=
D
s
I
I
(
)(
)
[
]
(
)
(
)(
)
[
]
570
,
0
90
,
0
15
,
4
96
,
0
5
07
,
0
2
1
,
0
07
,
0
5
,
0
5
,
0
1
15
,
4
5
2
1
,
0
5
,
0
5
4
4
0
=
⋅
−
⋅
⋅
+
+
−
=
=
+
⋅
−
⋅
+
+
−
=
ε
ξ
ξ
ξ
tg
I
K
s
Współczynnik parcia granicznego:
307
,
0
2
32
45
2
=
°
−
°
= tg
K
a
0
5,50
3,20
0,5
4,50
1,00
1,20
1,50
0,85
0,85
0,6
0,6
0,15
0,15
2,80 1,5
P
p = 14,0 kN/m
2
G
1
G
2
G
3
G
4
G
5
G
6
Grunt zasypowy:
Ps/Pd
I
D
= 0,60
γ
= 17,5 kN/m
3
φ
= 32
°
9
Współczynnik parcia pośredniego:
439
,
0
2
307
,
0
570
,
0
=
+
=
I
K
Wartości jednostkowe parcia gruntu:
15
,
6
439
,
0
0
,
14
1
=
⋅
=
⋅
=
I
K
p
e
kPa
13
,
21
439
,
0
)
95
,
1
5
,
17
0
,
14
(
2
=
⋅
⋅
+
=
e
kPa
76
,
5
439
,
0
75
,
0
5
,
17
3
=
⋅
⋅
=
e
kPa
[
]
65
,
37
439
,
0
)
40
,
1
75
,
0
95
,
1
(
5
,
17
0
,
14
4
=
⋅
+
+
⋅
+
=
e
kPa
40
,
48
439
,
0
)
50
,
5
5
,
17
0
,
14
(
5
=
⋅
⋅
+
=
e
kPa
Wypadkowe parcia gruntu i promienie ich działania względem środka podstawy fundamentu:
0
,
12
95
,
1
15
,
6
1
=
⋅
=
E
kN/m;
53
,
4
40
,
1
40
,
1
75
,
0
95
,
1
5
,
0
1
0
=
+
+
+
⋅
=
E
r
m
6
,
14
95
,
1
)
15
,
6
13
,
21
(
5
,
0
2
=
⋅
−
⋅
=
E
kN/m;
20
,
4
40
,
1
40
,
1
75
,
0
95
,
1
3
1
2
0
=
+
+
+
⋅
=
E
r
m
20
,
2
75
,
0
76
,
5
5
,
0
3
=
⋅
⋅
=
E
kN/m;
05
,
3
40
,
1
40
,
1
3
75
,
0
3
0
=
+
+
=
E
r
m
30
,
4
40
,
1
15
,
6
5
,
0
4
=
⋅
⋅
=
E
kN/m;
87
,
1
40
,
1
3
40
,
1
4
0
=
+
=
E
r
m
10
,
26
40
,
1
2
)
15
,
6
65
,
37
(
76
,
5
5
=
⋅
−
+
=
E
kN/m
94
,
1
40
,
1
40
,
1
)
15
,
6
65
,
37
76
,
5
(
3
)
15
,
6
65
,
37
(
76
,
5
2
5
0
=
+
⋅
−
+
⋅
−
+
⋅
=
E
r
m
60
,
8
40
,
1
15
,
6
6
=
⋅
=
E
kN/m;
70
,
0
40
,
1
5
,
0
5
0
=
⋅
=
E
r
m
60
,
51
40
,
1
2
15
,
6
40
,
48
15
,
6
65
,
37
7
=
⋅
−
+
−
=
E
kN/m;
67
,
0
40
,
1
)
15
,
6
40
,
48
15
,
6
65
,
37
(
3
)
15
,
6
4
,
48
(
)
15
,
6
65
,
37
(
2
5
0
=
⋅
−
+
−
⋅
−
+
−
⋅
=
E
r
m
0
1,40 1,95
p = 14,0 kN/m
2
0,75
1,40
φ
= 32
°
υ
a
= 61
°
5,50
e
1
e
2
e
3
e
4
e
5
E
1
E
2
E
3
E
5
E
4
E
6
E
7
υ
a
= 45
°
+
φ
/2 = 61
°
10
Zestawienie obciążeń poziomych na 1 mb ściany oporowej
Obc. Wartość charakt. H
k
r
0
M
0
(H
k
)
γ
F;A
H
d;A
M
0
(H
d;A
)
γ
F;B
H
d;B
M
0
(H
d;B
)
kN
m kNm kN kNm kN kNm
E
1
E
2
E
3
E
4
E
5
E
6
E
7
12,0
14,6
2,2
4,3
26,1
8,6
51,6
4,53
4,20
3,05
1,87
1,94
0,70
0,67
54,4
61,3
6,7
8,0
50,6
6,0
34,6
1,5
1,35
1,35
1,5
1,35
1,5
1,35
18,0
19,7
3,0
6,5
35,2
12,9
69,7
81,6
82,8
9,0
12,0
68,3
9,0
46,7
0,0
1,35
1,35
0,0
1,35
0,0
1,35
0,0
19,7
3,0
0,0
35,2
0,0
69,7
0,0
82,8
9,0
0,0
68,3
0,0
46,7
Σ
119,4
221,6
165,0
309,4
127,6
206,8
Kombinacje obciążeń:
Komb. 1:
7
,
266
1
;
=
k
V
kN/m;
4
,
119
1
;
=
k
H
kN/m;
1
,
65
6
,
221
5
,
156
1
;
=
+
−
=
k
M
kNm/m;
Komb. 2:
0
,
359
2
;
=
d
V
kN/m;
0
,
165
2
;
=
d
H
kN/m;
1
,
98
4
,
309
3
,
211
2
;
=
+
−
=
d
M
kNm/m;
Komb. 3:
7
,
266
3
;
=
d
V
kN/m;
0
,
165
3
;
=
d
H
kN/m;
9
,
152
4
,
309
5
,
156
3
;
=
+
−
=
d
M
kNm/m;
Komb. 4:
9
,
249
4
;
=
d
V
kN/m;
6
,
127
4
;
=
d
H
kN/m;
0
,
73
8
,
206
8
,
133
4
;
=
+
−
=
d
M
kNm/m;
Mimośrody wypadkowej obciążeń:
Komb. 1:
24
,
0
7
,
266
1
,
65
1
;
=
=
B
e
m <
53
,
0
6
2
,
3
6
=
=
B
m;
Komb. 2:
27
,
0
0
,
359
1
,
98
2
;
=
=
B
e
m <
53
,
0
6
2
,
3
6
=
=
B
m;
Komb. 3:
57
,
0
7
,
266
9
,
152
3
;
=
=
B
e
m >
53
,
0
6
2
,
3
6
=
=
B
m lecz 0,57 m <
80
,
0
4
2
,
3
4
=
=
B
m
Komb. 4:
29
,
0
9
,
249
0
,
73
4
;
=
=
B
e
m <
53
,
0
6
2
,
3
6
=
=
B
m;
Naciski na grunt pod płytą fundamentową dla Komb. 1:
=
⋅
+
⋅
⋅
=
)
2
,
3
24
,
0
6
1
(
0
,
1
2
,
3
7
,
266
1
;
k
q
120,8
kPa
=
⋅
−
⋅
⋅
=
)
2
,
3
24
,
0
6
1
(
0
,
1
2
,
3
7
,
266
2
;
k
q
45,8
kPa
0
q
1
e
Bk
Σ
V
k
2
1
B
q
2
Wyszukiwarka
Podobne podstrony:
Fundamentowanie cw cz 2 id 181 Nieznany
Fundamentowanie ćw cz 2
Fundamentowanie cw cz 8 cd id Nieznany
Fundamentowanie cw cz 9
Fundamentowanie cw cz 8 id 181 Nieznany
Fundamentowanie cw cz 5 id 181 Nieznany
Fundamentowanie ćw cz 2
więcej podobnych podstron