
A
KADEMIA
P
ODLASKA
Kierunek: CHEMIA
KRYSTALOCHEMIA
Materiały do ćwiczeń laboratoryjnych
SIEDLCE 2009
2
SYLABUS
Instytut Chemii Kierunek Chemia - studia stacjonarne
Nazwa
przedmiotu
Typ kursu
Sposób
zaliczenia kursu
Liczba godzin
semestr ECTS
Σ
w
ćw
lab
sem
Krystalochemia kierunkowy
Zaliczenie na
ocenę
45
15
30
3
3
Katedra
Katedra Chemii Organicznej i Stosowanej (rok akad. 2008/09)
Wykład
dr Zbigniew Karczmarzyk
Laboratorium
dr Zbigniew Karczmarzyk, mgr Waldemar Wysocki
Ćwiczenia
1.
Przedmioty wprowadzające z wymaganiami wstępnymi: Matematyka, Fizyka.
2.
Założenia i cele przedmiotu: Prawa klasycznej krystalografii geometrycznej w powiązaniu z
budową wewnętrzną kryształu. Symetria w morfologii i budowie wewnętrznej kryształów.
Klasyfikacja ciał krystalicznych i typy struktur krystalicznych. Związek między strukturą
krystaliczną a właściwościami chemicznymi i fizycznymi kryształów.
3.
Metody dydaktyczne: wykład: konwencjonalny, problemowy, środki audiowizualne, eksperyment
laboratoryjny, słowna metoda problemowa, eksperyment modelowy, pomiar z obliczeniami.
4.
Treści programowe:
Wykłady: Zakres i zastosowanie wyników badań krystalograficznych. Stan krystaliczny,
fenomenologiczna i mikroskopowa definicja kryształu. Prawa klasycznej krystalografii oraz
symetria w powiązaniu z budową wewnętrzną kryształu. Budowa i symetria sieci przestrzennej.
Elementy krystalochemii. Własności fizyczne kryształów
Ćwiczenia: Projekcja stereograficzna, goniometr optyczny. Sieć przestrzenna kryształu, komórka
elementarna, typy sieci Bravais’ego. Symetria w morfologii kryształów. Symetria w budowie
wewnętrznej kryształów. Przykłady struktur krystalicznych pierwiastków i związków chemicznych.
5.
Efekty kształcenia (umiejętności i kompetencje): Znajomość podstawowych pojęć i praw z
zakresu krystalografii geometrycznej i strukturalnej; umiejętność posługiwania się matematycznym
opisem postaci zewnętrznej kryształu oraz sieci przestrzennej kryształu; znajomość wybranych
struktur krystalicznych pierwiastków i związków chemicznych oraz umiejętność powiązania
struktury z właściwościami fizycznymi i chemicznymi substancji krystalicznej.
6.
Formy i warunki zaliczenia:
Wykład: zal/o; test kontrolny
Ćwiczenia laboratoryjne: zal/o; zaliczenie trzech kolokwiów kontrolnych.
7.
Wykaz literatury podstawowej:
1.Penkala T. „Zarys krystalografii”. PWN, Warszawa, 1977.
2. Bojarski, Z., Gigla, M., Stróż, K., Surowiec, M. „Krystalografia. Podręcznik wspomagany
komputerowo”, PWN, Warszawa, 1996, 2003.
3. Van Merche M., Fenau-Dupont J. „Krystalografia i chemia strukturalna”, PWN Warszawa,
1984.
8.
Wykaz literatury uzupełniającej:

3
KRYSTALOCHEMIA;
Chemia II, sem. III, studia licencjackie.
(rok akademicki 2009/20109)
Wykład:
15 godz.; 7 wykładów x 2 godz. + 1 godz. (kolokwium).
I. Wprowadzenie.
Historia krystalografii, krystalografia jako nauka, fenomenologiczna definicja kryształu.
II. Podstawowe prawa i pojęcia.
Sieć krystaliczna i przestrzenna, układy krystalograficzne, sieci Bravais’go, prawo stałości
kątów, czworościan zasadniczy, prawo wymiernych stosunków odcinków (prawo Haüy’ego),
prawo wymiernych wskaźników, prawo pasowe Weissa, obliczenia pasowe.
III. Symetria w morfologii kryształów.
Prawo symetrii, elementy symetrii kryształów, klasy symetrii, wyprowadzenie 32 klas
symetrii, metody eksperymentalne określania klasy symetrii kryształu, pokrój kryształów.
IV. Symetria w budowie wewnętrznej kryształów.
Strukturalne elementy symetrii, składanie elementów symetrii z translacją, grupy
przestrzenne.
V. Elementy krystalochemii.
Klasyfikacja ciał krystalicznych, liczby i wielościany koordynacyjne, promienie atomowe i
jonowe, przykłady struktur kryształów, polimorfizm, izotypia, izomorfizm.
VI. Wybrane zagadnienia krystalofizyki.
Symetria własności fizycznych a symetria struktury - zasada Neumana i grupy graniczne
Curie, piroelektryczność, piezoelektryczność.
Zaliczenie wykładu:
Test zaliczeniowy obejmujący 15 pytań z 5 możliwościami wyboru poprawnej odpowiedzi do
każdego pytania. Maksymalna liczba punktów z testu wynosi 15, po 1 punkcie za każdą
poprawną odpowiedź. Ocena końcowa zależy od sumy uzyskanych punktów:
0 - 7 pkt
2.0
ndst
8 - 9 pkt
3.0
dst
10 - 11 pkt 3.5
dst +
12 - 13 pkt 4.0
db
14 pkt
4.5
db +
15 pkt
5.0
bdb
Ćwiczenia laboratoryjne
: 30 godz.; 10 ćwiczeń x 3 godz.
Ćwiczenie 1. Organizacja zajęć, pokaz substancji krystalicznych. Wprowadzenie do projekcji
stereograficznej kryształów.
Ćwiczenie 2. Projekcja stereograficzna - operacje z wykorzystaniem siatki Wulfa, cz. 1.
Goniometr optyczny – projekcja stereograficzna rzeczywistego kryształu.
Ćwiczenie 3. Projekcja stereograficzna - operacje z wykorzystaniem siatki Wulfa, cz. 2.
Goniometr optyczny – projekcja stereograficzna rzeczywistego kryształu.
Ćwiczenie 4. Kolokwium nr 1. Sieć przestrzenna kryształu, komórka elementarna, typy sieci
Bravais’ego.

4
Ćwiczenie 5. Matematyczny opis sieci przestrzennej kryształu (węzły, proste sieciowe,
płaszczyzny sieciowe) i postaci zewnętrznej kryształu (krawędzie, ściany); wskaźniki
prostych sieciowych i krawędzi, wskaźniki Millera płaszczyzn sieciowych i ścian, rachunek
pasowy.
Ćwiczenie 6. Kolokwium nr 2. Symetria w morfologii kryształów, cz. 1. Klasy symetrii w
układzie rombowym, tetragonalnym i regularnym.
Ćwiczenie 7. Symetria w morfologii kryształów, cz. 2. Klasy symetrii w układzie
jednoskośnym, trygonalnym i heksagonalnym.
Ćwiczenie 8. Strukturalne elementy symetrii, kombinacje elementów symetrii z translacją,
wprowadzenie do symetrii grup przestrzennych - symetria obrazów Eschera, grupy
przestrzenne i ich opis w Międzynarodowych Tablicach Krystalograficznych.
Ćwiczenie 9. Wybrane struktury pierwiastków i związków chemicznych: Cu, α-W, Mg, C
(diament, grafit, fulereny), NaCl, CsCl, ZnS (blenda cynkowa, wurcyt), FeS
2
(CO
2
), CaF
2
;
obliczenia krystalochemiczne.
Ćwiczenie 10. Kolokwium nr 3. Zaliczenie ćwiczeń.
Zaliczenie ćwiczeń laboratoryjnych:
W ramach ćwiczeń przeprowadzone są 3 kolokwia. Maksymalna suma punktów z kolokwiów
wynosi 30, po 10 punktów z każdego kolokwium. Ocena końcowa z ćwiczeń zależy od sumy
uzyskanych punktów:
0 - 15.0 pkt
2.0
ndst
15.5 - 18.0 pkt
3.0
dst
18.5 - 21.0 pkt
3.5
dst +
21.5 - 24.0 pkt
4.0
db
24.5 - 27.0 pkt
4.5
db +
27.5 - 30.0 pkt
5.0
bdb
Uwagi:
1. W ramach ćwiczeń laboratoryjnych studenci powinni wykonać samodzielnie ćwiczenia i
zadania wykorzystując program komputerowy KRYS (Bojarski i inni, 1996, 2003) ilustrujący
podstawowe operacje i obliczenia krystalograficzne.
2. Materiały do ćwiczeń należy pobrać ze strony
krystalochemia_materiały_2009.zip
3. Terminy kolokwiów nie podlegają negocjacji.
5
Ćwiczenie 1.
Organizacja zajęć, pokaz substancji krystalicznych. Wprowadzenie do projekcji
stereograficznej kryształów.
Ćwiczenie 2-3.
Projekcja stereograficzna - operacje z wykorzystaniem siatki Wulfa. Goniometr
optyczny – projekcja stereograficzna rzeczywistego kryształu.
Zadanie 1.
Dane są bieguny stereograficzne ścian kryształu o współrzędnych (φ, σ):
a) (20
o
, 50
o
) i (120
o
, 60
o
)
b) (20
o
, 90
o
) i (170
o
, 90
o
)
c) (130
o
, 112
o
) i (70
o
, 38
o
)
Określić kąt między podanymi parami ścian kryształu.
Zadanie 2.
Zmierzyć kąt Φ między wszystkimi możliwymi parami różnych biegunów P o następujących współrzędnych
kątowych (φ, σ): P
1
(47
o
, 61
o
), P
2
(140
o
, 46
o
), P
3
(211
o
, 116
o
), P
4
(304
o
, 108
o
), P
5
(80
o
, 90
o
), P
6
(260
o
, 90
o
).
Zadanie 3.
Współrzędne kątowe (φ, σ) dwóch ścian kryształu wynoszą: P
1
(20
o
, 70
o
) i P
2
(130
o
, 80
o
).
a) Zmierzyć kąt α między rzutami stereograficznymi płaszczyzn P
1
i P
2
.
b) Wykreślić koło pasowe K dla tych płaszczyzn, znaleźć biegun osi pasa N i określić jego współrzędne kątowe.
Zadanie 4.
Zmierzyć kąt Ψ między dwoma kołami pasowymi K
1
i K
2
na płaszczyźnie projekcji stereograficznej oraz kąt Φ
między osiami pasów, jeśli koło K
1
przechodzi przez bieguny płaszczyzn P
1
(140
o
, 46
o
) i P
2
(47
o
, 61
o
), a koło
wielkie K
2
jest kołem pasowym płaszczyzn P
3
(197
o
, 44
o
) i P
4
(344
o
, 62
o
).
Zadanie 5.
Za pomocą siatki Wulfa znaleźć rzuty stereograficzne ścian kryształu o następujących współrzędnych (φ, σ):
A(0
o
, 90
o
), B(40
o
, 110
o
), C(0
o
, 0
o
), D(0
o
, 180
o
), E(0
o
, 70
o
), F(20
o
, 50
o
).
Dla każdego rzutu znaleźć punkty odpowiadające przesunięciu danej ściany o kąt:
a) φ = 30
o
, 90
o
, 120
o
przy kącie σ bez zmian.
b) σ = 40
o
, 60
o
, 90
o
przy kącie φ bez zmian.
Zadanie 6.
Dany jest rzut stereograficzny ściany kryształu i prosta. Znaleźć odpowiednie rzuty ścian po obrocie względem
prostej o podany kąt.
Prosta
(φ, σ)
Współrzędne kątowe ściany
(φ, σ)
Kąt obrotu α
(0
o
, 0
o
)
(0
o
, 90
o
), (0
o
, 70
o
), (50
o
, 78
o
), (90
o
, 90
o
)
60
o
, 90
o
, 120
o
, 240
o
(90
o
, 90
o
)
(90
o
, 90
o
), (90
o
, 70
o
), (45
o
, 90
o
), (100
o
, 68
o
)
45
o
, 90
o
, 180
o
(0
o
, 90
o
)
(0
o
, 0
o
), (0
o
, 90
o
), (0
o
,60
o
)
45
o
, 90
o
, 180
o
Zadanie 7.
Znaleźć na płaszczyźnie projekcji stereograficznej punkt P
x
, który z punktem P
1
(30
o
, 90
o
) i z punktem P
2
(50
o
,
60
o
) tworzy kat 40
o
. Podać współrzędne kątowe (φ
x
, σ
x
) punktu P
x
.
Zadanie 8.
W sześcianie występuje 9 płaszczyzn symetrii oraz 4 osie trójkrotne. Wykreślić na siatce Wulfa ślady kół
wielkich odpowiadające tym płaszczyznom. Znaleźć kąty między osiami trójkrotnymi oraz kąty między
płaszczyznami.

6
Zadanie 9.
Dokonać pomiaru kątów między ścianami w krysztale rzeczywistym z wykorzystaniem dwukołowego
goniometru optycznego oraz wykonać projekcja stereograficzna kryształu zgodnie z następującymi poleceniami:
a) Zapoznać się z budową i zasadą działania dwukołowego goniometru optycznego.
b) Obracając kryształ względem koła φ w zakresie od 0 do 360˚ przy kącie σ = 90˚, wprowadzić kolejno ściany
w położenie odbijające światło. Dla każdej ściany w tym położeniu zanotować współrzędne (φ, σ) oraz
przerysować obserwowany kształt ściany.
c) Ustawić kolejne ściany w położeniu odbijającym (σ = 90˚) i przy kącie φ = const. Obracać kryształ względem
koła σ zmieniając kąt σ w dopuszczalnym przez konstrukcję goniometru zakresie wprowadzając ściany w
położenie odbijające światło. W położeniu tym odczytywać i zanotować współrzędne (φ, σ) oraz obserwowany
kształt ściany.
d) Posługując się siatką Wulfa nanieść zmierzone bieguny ścian kryształu na płaszczyznę koła projekcji.
e) Dokonać pomiaru kątów między parami wszystkich zmierzonych ścian wykorzystując skalę kątową siatki
Wulfa.
f) Zbadać symetrię w rozkładzie biegunów ścian na projekcji stereograficznej.
Ćwiczenie 4.
Sieć przestrzenna kryształu, komórka elementarna, typy sieci Bravais’ego.
Zadanie 1.
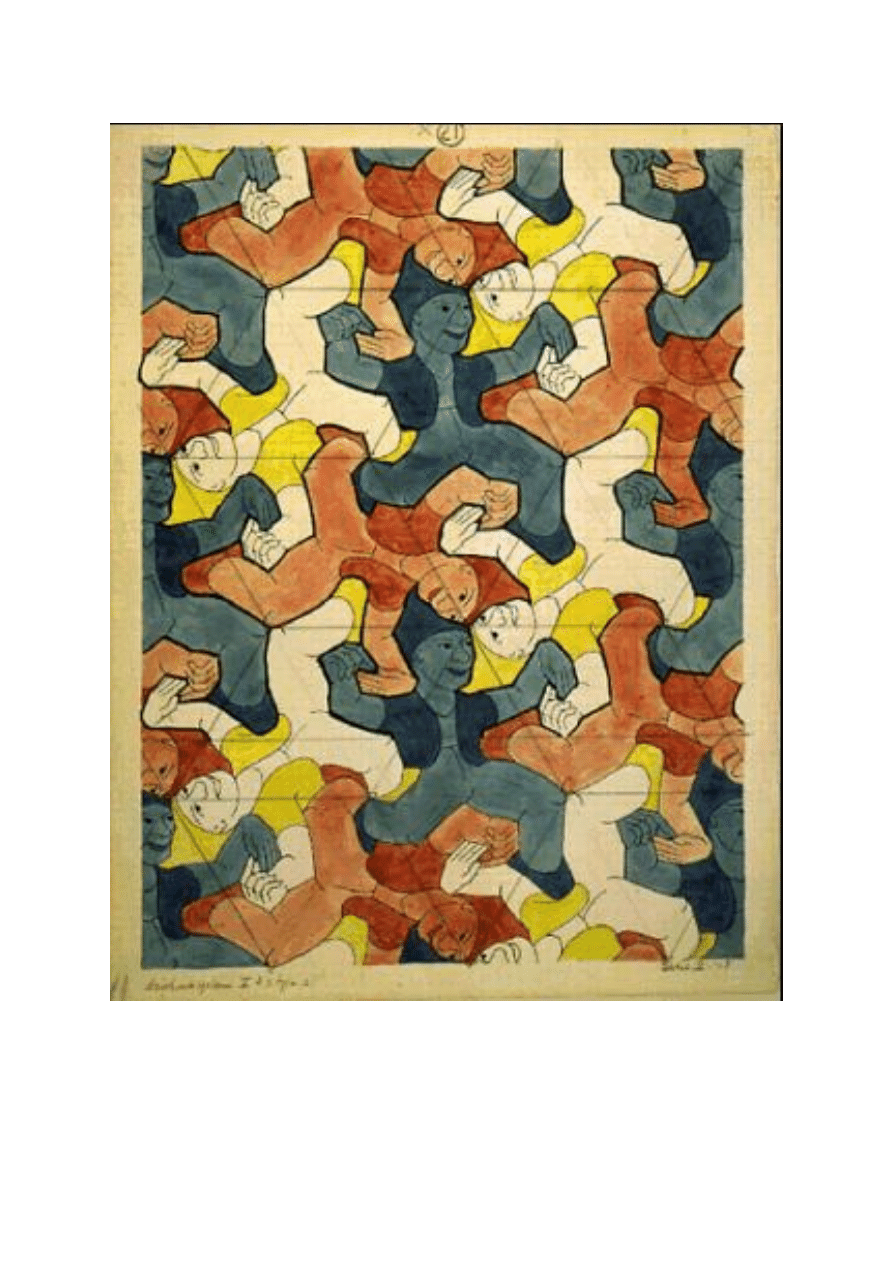
Na załączonych grafikach Eschera oraz rysunkach (i) – (xv)
1
/patrz suplement/ znaleźć charakterystyczny motyw
wzoru, obrać podstawowe kierunki translacji, narysować odpowiadającą wzorowi (dwuwymiarowej sieci
krystalicznej) płaszczyznę sieciową (dwuwymiarową sieć przestrzenną) i zaznaczyć na niej równoległobok
elementarny.
Zadanie 2.
Na modelach komórek elementarnych określić:
a) stałe sieciowe a, b, c;
b) układ krystalograficzny
c) typ sieci Bravais’go ( P, I, F, C, A, B);
d) współrzędne węzłów sieci;
e) liczbę węzłów przypadających na komórkę elementarną;
f) wykonać rzut prostopadły na płaszczyznę XY z zaznaczeniem współrzędnych węzłów sieci..
Zadanie 3.
W sieci przestrzennej układu rombowego 2 atomy tego samego rodzaju zajmują następujące położenia:
a) 0, ½, 0 i ½, 0, ½
b) 0, 0, ½ i ½, ½, ½
c) 0, 0, ½ i ½, 0, 0
Określić typ sieci Bravais’go.
Zadanie 4.
W układzie regularnym 4 atomy tego samego rodzaju zajmują położenia: ½, 0, 0; 0, ½, 0; 0, 0, ½ oraz ½, ½, ½.
Określić typ sieci Bravais’go.
Zadanie 5.
W układzie rombowym 2 atomy tego samego rodzaju zajmują położenia: ½, 0, 0 i 0, ½, ½, a dwa inne atomy
następujące położenia: 0, 0, ½ i ½, ½, 0. Określić typ sieci Bravais’go.
Zadanie 6.
Wykazać, że centrowanie sieci tetragonalnej P na podstawie (typ C) daje również sieć typu P, a centrowanie na
ścianach (typ F) daje sieć typu I.
Zadanie 7.
Zakładając, że atomy są sztywnymi kulami o średnicy D i zajmują pozycje węzłów w komórkach typu
odpowiednio P, I, F, obliczyć:
a) objętość komórek wyrażonych w wartościach D,
b) liczbęatomów w komórce,
c) gęstość wyrażoną liczbą atomów przypadających na daną objętość komórki elementarnej.
1
Copyright 2001 International Union of Crystallography

7
Ćwiczenie 5.
Matematyczny opis sieci przestrzennej kryształu (węzły, proste sieciowe,
płaszczyzny sieciowe) i postaci zewnętrznej kryształu (krawędzie, ściany); wskaźniki prostych
sieciowych i krawędzi, wskaźniki Millera płaszczyzn sieciowych i ścian, rachunek pasowy.
Zadanie 1.
W rzucie prostopadłym na płaszczyznę XY narysować sieć płaską układu rombowego.
a) Wykreślić proste o wskaźnikach: [100], [010], [110], [210], [130], [
2
1 0].
b) Obliczyć wskaźniki prostych przechodzących przez pary punktów o współrzędnych: 000 i 110; 000 i 120;
120 i
½ ½ 0; 230 i 100; 020 i 200. Wykreślić te proste na rysunku z punktu a).
Zadanie 2.
Na rysunku perspektywicznym krystalograficznego układu współrzędnych zaznaczyć płaszczyzny o
wskaźnikach: (100), (010), (001), (111), (212), (123).
Zadanie 3.
W rzucie prostopadłym na płaszczyznę XY narysować sieć płaską z układu tetragonalnego. Zaznaczyć kilka
równoległych płaszczyzn o wskaźnikach: (110), (210), (120), (320), (1
2
0), (
2
1 0).
Zadanie 4.
Stałe sieciowe kryształu wynoszą a, b, c. Obliczyć symbole Millera dla ścian kryształu, które odcinają na osiach
krystalograficznych X, Y, Z odcinki wynoszące odpowiednio:
a) 6a, 12b, 3c
b) 4a, 3b, 2c
c) 4a, 6b, 2c
d) (1/2)a, (1/2)b, (1/3)c
Zadanie 5.
Płaszczyzny P, R, W w sieci przestrzennej kryształu tetragonalnego odcinają na osiach krystalograficznych
odcinki:
płaszczyzna P: x = 18.0 Å, y = 18.0 Å, z = 8.5 Å,
płaszczyzna R: x = 8.0 Å, y = 8.0 Å, z = 17.0 Å,
płaszczyzna W: x = 12.0 Å, y = 12.0 Å, z = 17.0 Å.
Podać wskaźniki Millera płaszczyzn przyjmując płaszczyznę W jako jednostkową.
Zadanie 6.
Zamienić symbole trójwskaźnikowe na symbole czterowskaźnikowe następujących płaszczyzn w układzie
heksagonalnym: (110), (210), (
1
1 1), (201), (011). Narysować linie przecięcia tych płaszczyzn z płaszczyzną
(0001) komórki heksagonalnej.
Zadanie 7.
Ściana kryształu heksagonalnego równoległa do osi Z odcina na osiach X i U odcinki 2a i -3a. Znaleźć symbol
(hk
i
l) ściany.
Zadanie 8.
a) Obliczyć symbole Millera (hkl) płaszczyzn oraz symbole [uvw] kierunków w sześcianie i ośmiościanie.
b) W każdej z tych brył geometrycznych wskazać liczbę pasów oraz liczbę ścian w każdym pasie.
Zadanie 9.
Sprawdzić, czy dane ściany leżą w jednym pasie:
a) (111), (231), (1
2
4)
b) (201), (010), (211)
Jeśli tak, to obliczyć symbol osi tego pasa.
Zadanie 10.
Sprawdzić, czy dane kierunki leżą w jednej płaszczyźnie:
a) [110], [001], [111]
b) [232], [112], [120]
Jeśli tak, to obliczyć wskaźniki Millera tej płaszczyzny.

8
Zadanie 11.
Komórka elementarna kryształu α-Fe należy do układu regularnego i jest przestrzennie centrowana. Długość
krawędzi komórki elementarnej wynosi a = 2.86 Å. Obliczyć odległość między środkami najbliższych atomów
znajdujących się na kierunku [111] oraz [110] na podstawie rozważań geometrycznych w sześcianie.
Ćwiczenie 6-7.
Symetria w morfologii kryształów, Klasy symetrii w układzie rombowym,
tetragonalnym, regularnym, trygonalnym, heksagonalnym i jednoskośnym.
Zadanie 1.
Na modelach postaci prostych kryształów określić:
a) elementy symetrii,
b) klasę krystalograficzną i układ krystalograficzny,
c) narysować rzut stereograficzny ścian modelu,
d) podać symbole i nazwy postaci prostych oraz liczbę ścian w tych postaciach.
Zadanie 2.
Narysować rzuty stereograficzne, podać wszystkie elementy symetrii, nazwę i symbol klasy krystalograficznej,
w której występuje minimum następujących elementów symetrii:
a) L
Z
2
+ L
y
2
b) L
Z
4
+ L
Y
2
c) L
Y
2
.
C
d) L
Z
6
+ C
e) L
Z
4.
C
f) L
Z
4
+ P
Z
g) L
Y
2
+ C
h) L
Z
3
+ L
Y
2
i) L
Z
4
+ C + L
Y
2
j) L
Z
4
+ L
Y
2.
C
k) L
Z
2
+ P
Y
l) L
Z
4
+ P
Y
m) L
Z
3
+ P
Y
o) L
[1 1 1]
3
+ L
[ 1 11]
3
p) L
Z
6
+ L
Y
2
r) L
Z
6
+ L
Y
2
+ C
s) L
[1 1 1]
3
+ L
[ 1 11 ]
3
+ C
t) L
[111]
3
+ L
[ 1 1 1]
3
+L
[0 1 1 ]
2
u) L
Z
2
+ L
Y
2.
C
Wykonać projekcję stereograficzną postaci prostych ogólnej i szczególnych, podać ich nazwy, symbole oraz
liczebność.
Uwaga: dolny indeks przy symbolu osi symetrii oznacza, że oś symetrii jest równoległa do podanej osi
krystalograficznej; indeks przy symbolu płaszczyzny oznacza, że płaszczyzna jest prostopadła do podanej osi
krystalograficznej.
Zadanie 3.
Wykonać projekcje stereograficzne ściany
a) (hk0) w klasach układu rombowego;
b) (hhl) w klasach układu tetragonalnego;
c) (h 0
h
l) w klasach układu trygonalnego.
Podaj nazwy i liczebności otrzymanych postaci prostych.
Zadanie 4.
Podać nazwę i elementy symetrii klasy krystalograficznej, która powstanie, jeśli do elementów symetrii klasy
a) jednościanu dodać środek symetrii;
b) daszka dodać środek symetrii;
c) czworościanu rombowego dodać płaszczyznę symetrii prostopadłą do dowolnej osi dwukrotnej;
d) piramidy trygonalnej dodać oś dwukrotną prostopadłą do osi trójkrotnej;
e) czworościanu tetragonalnego dodać oś dwukrotną prostopadłą do osi czterokrotnej inwersyjnej;
f) trapezoedru heksagonalnego dodać środek symetrii.
g) dwunastościanu tetraedrycznopentagonalnego dodać środek symetrii.
Zadanie 5.
Dla każdej klasy krystalograficznej wskazać minimum elementów symetrii niezbędne do wyprowadzenie tej
klasy. Wykonać projekcję stereograficzną elementów symetrii klasy krystalograficznej.
Ćwiczenie 8.
Strukturalne elementy symetrii, kombinacje elementów symetrii z translacją,
wprowadzenie do symetrii grup przestrzennych.
Zadanie 1.
Płaszczyzny poślizgu a, c, n, d są równoległe do płaszczyzny XZ układu osi współrzędnych i przechodzą przez
początek układu. Jakie zmiany współrzędnych punktu P(x, y, z) powodują te płaszczyzny?
Zadanie 2.
Oś śrubowa
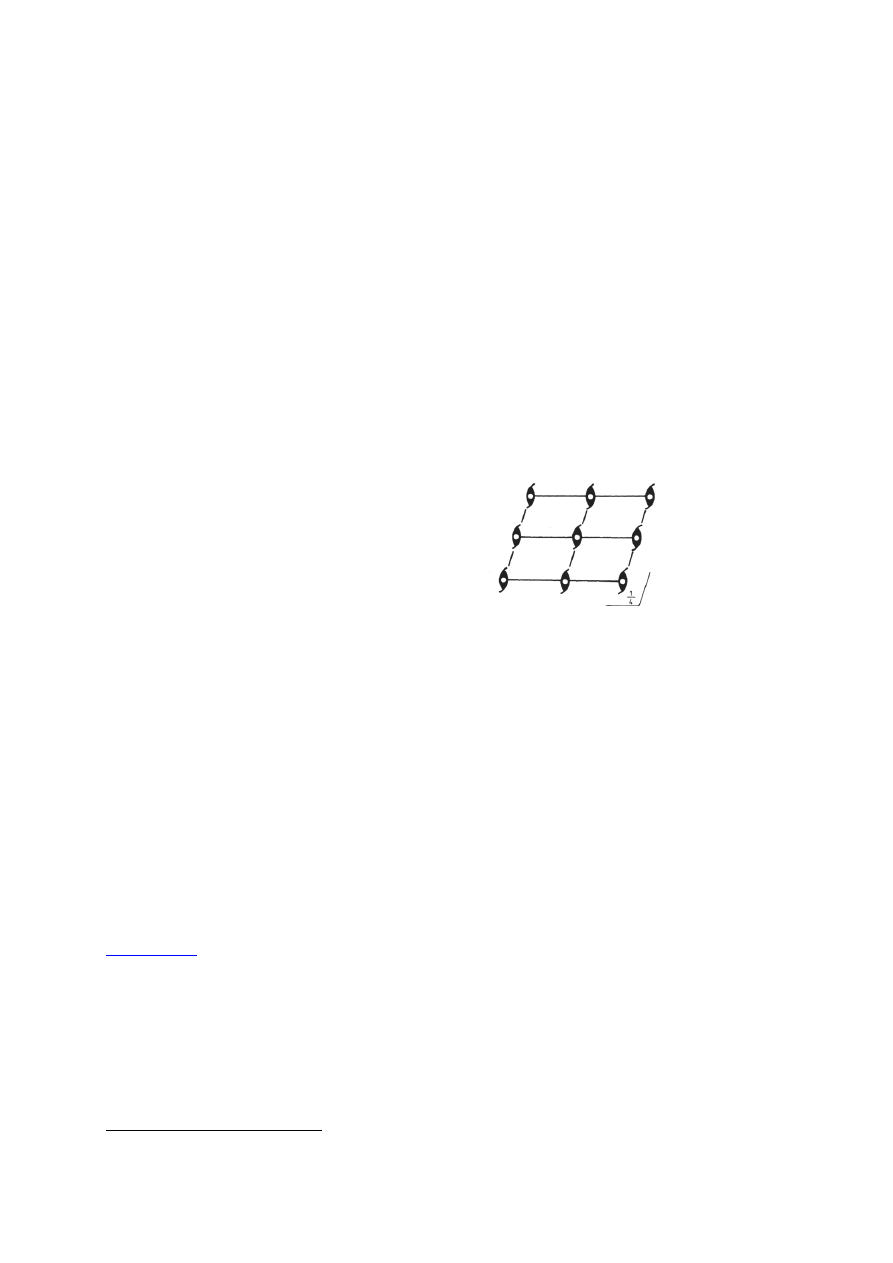
9
a) 2
1
b)3
1
c)3
2
d)4
1
e)4
2
f)4
3
g)6
1
h)6
2
i)6
3
j)6
4
k) 6
5
jest równoległa do osi Z. Jakie współrzędne ma zespół punktów symetrycznie równoważnych powstający w
wyniku działania tej osi?
Zadanie 3.
Rozwiązać zadanie 1 i 2 posługując się macierzowym przedstawieniem elementów symetrii.
Zadanie 4.
W komórce elementarnej sieci przestrzennej kryształu istnieje środek symetrii w węźle 000. Podać współrzędne
środków symetrii jakie zostaną wygenerowane w wyniku działania translacji podstawowych sieci na ten środek
symetrii.
Zadanie 5.
Jakie nowe elementy symetrii generują osie
a) 2
b) 4
c) 3
1
d)4
1
e) 4
2
f) 6
g) 6
4
powielone translacyjnie w kierunkach prostopadłych do tych osi? Podać symbole wygenerowanych grup
przestrzennych oraz liczebność i współrzędne punktów symetrycznie równoważnych w pozycji ogólnej i
pozycjach szczególnych.
Zadanie 6.
Dla grupy przestrzennej P112
1
/m, w której rozmieszczenie
elementów
symetrii
przedstawia
rysunek,
podać
współrzędne
pozycji
punktów
symetrycznie
równoważnych, gdy punkt
wyjściowy ma współrzędne:
a) x, y, z
b) x, y, 1/4
c) 0, 0, 0
Ustalić symetrię własną punktów.
Zadanie 7
Rysunki (i) – (xv)
2
przedstawiają rzuty punktów symetrycznie równoważnych dla różnych grup przestrzennych.
Dla każdej grupy przestrzennej
a) narysować rzut komórki elementarnej oraz rozkład elementów symetrii,
b) podać układ krystalograficzny oraz jej symbol,
c) podać współrzędne punktów symetrycznie równoważnych.
Zadanie 8.
Podano symbole grup przestrzennych kilku kryształów:
a) P222
1
b) P2
1
/c
c) Pba2
d) P4/nbc
e) Fd3
f) P3
1
Do jakich grup punktowych (klas krystalograficznych) należą te kryształy?
Zadanie 9.
Podać rozmieszczenie elementów symetrii w komórce elementarnej dla grupy przestrzennej P4
2
. Wypisać
współrzędne punktów symetrycznie równoważnych, określić ich liczebność, oznaczenia Wyckoffa i symetrię
własną tych punktów.
Ćwiczenie 9.
Wybrane struktury pierwiastków i związków chemicznych: Cu, α-W, Mg, C
(diament, grafit, fulereny), NaCl, CsCl, ZnS (blenda cynkowa, wurcyt), FeS
2
(CO
2
), CaF
2
.
Zadanie 1.
Na modelach struktur krystalicznych pierwiastków i związków chemicznych określić:
a) komórkę elementarną i jej parametry,
b) układ krystalograficzny, grupę przestrzenną i klasę krystalograficzną,
c) wielościany koordynacyjne i liczby koordynacyjne,
d) makroskopowe i strukturalne elementy symetrii.
2
Copyright 2001 International Union of Crystallography

10
Wykonać rzut komórki elementarnej na płaszczyznę XY przyjmując, że atomy (jony) są sztywnymi kulami o
promieniach proporcjonalnych do promieni atomowych (jonowych). Zaznaczyć elementy symetrii.
Zadanie 2.
Wyrazić promienie atomowe poprzez krawędź komórki elementarnej a, dla struktur A1 (miedź), A2 (wolfram
α), A3 (magnez), A4 (diament). Na podstawie uzyskanych wyników obliczyć promienie atomowe dla złota (a =
4.0786 Å), niklu (a = 3.5168 Å), molibdenu (a = 3.1668 Å ), żelaza α (a = 2.8607 Å), tytanu (a = 2.9504 Å),
cynku (a = 2.6595 Å), germanu (a = 5.6576 Å), cyny szarej (a = 6.46 Å).
Zadanie 3.
Obliczyć stosunek promieni atomowych R
A
/R
B
(R
A
- promień atomu koordynowanego, R
B
- promień atomu
koordynujacego), zakładając, że atomy B stykają się ze sobą, dla następujących wielościanów lub wielokątów
koordynacyjnych:
a) sześcian, b) ośmiościan, c) kwadrat, d) trójkąt.
Zadanie 4.
Wyznaczyć stopień wypełnienia przestrzeni dla struktur typu A1 (miedź), A2 (wolfram α), A3 (magnez), A4
(diament).
Wskazówka: Stopień wypełnienia przestrzeni można określić następującym wzorem: w = (ZV
A
)/V
K
gdzie: Z - liczba atomów w komórce elementarnej, V
A
- objętość jednego atomu, V
K
- objętość komórki
elementarnej.
Zadanie 5.
Obliczyć maksymalny promień atomu międzywęzłowego, jaki można umieścić w sieci krystalicznej Cu bez jej
zaburzenia. Długość krawędzi komórki elementarnej Cu wynosi a = 3.61 Å.
Wskazówka: Sieć krystaliczna miedzi zawiera luki tetraedryczne i oktaedryczne, przy czym w luce
oktaedrycznej można umieścić atom o większym promieniu niż w luce tetraedrycznej.
Zadanie 6.
Obliczyć długość wiązania miedzy jonami K
+
i Cl
-
w krysztale KCl (struktura typu NaCl), wykorzystując w tym
celu następujące dane: 1 mol cząsteczek KCl ma masę μ = 74.56 g/mol, gęstość wynosi d = 1.990 g/cm
3
, stała
Avogadro N
A
= 6.022
.
10
23
1/mol.
Zadanie 7.
Gęstość glinu mającego strukturę typu A1 (miedzi) wynosi 2.699 g/cm
3
, masa molowa jego atomów jest równa
26.97 g. Obliczyć:
a) ile moli zawiera 1 m
3
stałego glinu,
b) ile atomów zawiera 1 m
3
stałego glinu,
c) parametr a komórki elementarnej glinu,
d) promień atomu glinu,
e) masę jednego atomu glinu.
Zadanie 8.
Z jakich elementów składa się motyw w strukturach A1 (miedź), A2 (wolfram α), A3 (magnez), A4 (diament),
A9 (grafit), B1 (NaCl), B2 (CsCl), B3 (ZnS - blenda cynkowa), B4 (ZnS - wurcyt).
11
SUPLEMENT
Przykładowe ćwiczenia do programu KRYST1.
I. Uruchomić program KRYST1.EXE.
II. Z menu głównego wybrać następujące opcje:
1. Opcja: Projekcje.
a) Opcja: Stereograficzne (konstr.)
- wybrać płaszczyznę projekcji (001),
- zaznaczyć bieguny ścian: (100), (010), (001), (112), (123), (1
1
3), (22
3
), (
111
) itp.
b) Opcja: Cyklograficzne (konstr.)
- wybrać płaszczyznę projekcji (001),
- zaznaczyć bieguny ścian: (100), (010), (001), (112), (123), (1
1
3), (22
3
), (
111
) itp.
c) Opcja: Porównanie
- wybrać stałe sieciowe: a = 10, b = 10, c = 10, α 90.0, β = 90.0, γ = 90.0;
- wybrać kierunek prostopadły do koła projekcji [001],
- powtórzyć operacje dla innych stałych sieciowych.
2. Opcja: Układy-wskaźnikowanie.
a) Opcja: Prezentacja układów krystalograficznych
- wybrać układ regularny,
- zadać płaszczyznę równoległą do płaszczyzny ekranu,
- operacje powtórzyć dla pozostałych układów krystalograficznych.
b) Opcja: Wskaźnikowanie kier. i płasz.
- Opcja: Rysowanie płaszczyzn o danych wskaźnikach: zadać płaszczyzny - (100), (010), (001), (112), (123),
(1
1
3), (22
3
), (
111
) i inne.
- Opcja: Rysowanie kierunków o danych wskaźnikach: zadać kierunki – [100], [010], [001], [111], [110], [101],
[011], [123], [321], [22
3
] i inne.
- Opcja: Wskaźnikowaniem płaszczyzn: wpisać wyliczone wskaźniki płaszczyzny wskazanej przez program i
zapoznać się z oceną programu.
- Opcja: Wskaźnikowanie kierunków: wpisać wyliczone wskaźniki kierunku wskazanego przez program i
zapoznać się z oceną programu.
3. Opcja: Symetria.
a) Opcja: Prezentacja elem. symetrii
- wybrać z listy element symetrii,
- zapoznać się z prezentacją.
b) Opcja: Prezentacja grup punktowych
-wybrać z listy grupę punktową (klasę krystalograficzną) w układzie krystalograficznym,
- klawiszem SPACE wprowadzać kolejne elementy symetrii grupy punktowej,
- zapoznać się z projekcją stereograficzną elementów symetrii wybranej grupy punktowej.
c) Opcja: Generowanie grup punktowych
- wprowadzić główną oś symetrii w kierunku [001]dla wskazanej przez program grupy punktowej,
- wprowadzić jeden lub dwa inne elementy symetrii niezbędne do wygenerowania wskazanej grupy punktowej.
- zapoznać się z oceną programu.

12
ZESTAWIENIE UKŁADÓW KRYSTALOGRAFICZNYCH
Układ
Parametry komórki elementarnej
Typ sieci Bravais’go
----------------------------------------------------------------------------------------------------------------------------------------
Trójskośny
α
β
γ
α
a
b
c
a
P
α, β, γ
90
o
Jednoskośny
α = γ = 90
O
, β
90
O
a
b
c
a
P, C
(β > 90
o
)
Rombowy
α = β = γ = 90
O
a
b
c
a
P, I, F, C (A, B)
Tetragonalny
α = β = γ = 90
O
a = b
c
P, I
Trygonalny
α = β = 90
O
, γ = 120
O
a = b
c
P
(Romboedryczny)
α = β = γ
90
O
a = b = c
R
Heksagonalny
α = β = 90
O
, γ = 120
O
a = b
c
P
Regularny
α = β = γ = 90
O
a = b = c
P, I, F

13
NAZWY I SYMBOLE 32 KLAS SYMETRII
Układ
krystalograficzny
Nazwa klasy
krystalograficznej
Symbol klasy
Grotha
Symbol H-M*
układ
trójskośny
klasa jednościanu
klasa dwuścianu
[-]
[C]
1
1
układ jednoskośny
klasa sfenoidu (daszka osiowego)
klasa daszka
klasa słupa jednoskośnego
[L
2
]
[P]
[PL
2
C]
2
m
2/m
układ
rombowy
klasa czworościanu rombowego
klasa piramidy rombowej
klasa podwójnej piramidy rombowej
[3L
2
]
[2PL
2
]
[3P3L
2
C]
222
mm2
mmm
układ
trygonalny
klasa piramidy trygonalnej
klasa romboedru
klasa trapezoedru trygonalnego
klasa piramidy dytrygonalnej
klasa skalenoedru dytrygonalnego
[L
3
]
[L
3
C]
[L
3
3L
2
]
[3PL
3
]
[3PL
3
3L
2
C]
3
3
32
3m
3 m
układ
tetragonalny
klasa piramidy tetragonalnej
klasa podwójnej piramidy
tetragonalnej
klasa trapezoedru tetragonalnego
klasa piramidy dytetragonalnej
klasa podwójnej piramidy
dytetragonalnej
klasa czworościanu tetragonalnego
klasa skalenoedru tetragonalnego
[L
4
]
[PL
4
C]
[L
4
4L
2
]
[4PL
4
]
[5PL
4
4L
2
C]
[L
2
]
[2P3L
2
]
4
4/m
422
4mm
4/mmm
4
4
2m
układ
heksagonalny
klasa piramidy heksagonalnej
klasa podwójnej piramidy
heksagonalnej
klasa trapezoedru heksagonalnego
klasa piramidy dyheksagonalnej
klasa podwójnej piramidy
dyheksagonalnej
[L
6
]
[PL
6
C]
[L
6
6L
2
]
[6PL
6
]
[7PL
6
6L
2
C]
6
6/m
622
6mm
6/mmm
14
układ
heksagonalny c.d.
klasa podwójnej piramidy trygonalnej
klasa podwójnej piramidy
dytrygonalnej
[PL
3
]
[4PL
3
3L
2
]
6
6 2m
układ
regularny
klasa dwunastościanu tetraedryczno-
pentagonalnego
klasa dwunastościanu podwójnego
klasa dwudziestoczterościanu
pentagonalnego
klasa czworościanu poszóstnego
klasa czterdziestoośmiościanu
[3L
2
4L
3
]
[3P3L
2
4L
3
C]
[3L
4
4L
3
6L
2
]
[6P3L
2
4L
3
]
[9P3L
4
4L
3
6L
2
C]
23
m3
432
4
3m
m3m
* Symbole Hermana-Mauguina (międzynarodowe) skrócone.
MIĘDZYNARODOWE SYMBOLE KLAS KRYSTALOGRAFICZNYCH HERMANA-MAUGUINA
W symbolice Hermana-Mauguina elementy symetrii mają następujące symbole:
1, 2, 3, 4, 5, 6,
1
,
2
(
m), 3 (
3+1),
4
, 6 (
3+m).
Symbol klasy krystalograficznej składa się z symboli elementów symetrii stanowiących niezbędne minimum do
wyprowadzenia danej klasy zapisanych w systemie pozycyjnym zgodnie z następującymi zasadami:
1. W układzie trójskośnym ze względu na występowanie jedynie elementu 1 lub 1 nie ma ustaleń.
2. W układzie jednoskośnym przyjmuje się, że charakterystyczna oś dwukrotna jest zorientowana równolegle do
jednej z dwóch osi krystalograficznych Y lub Z.
3. W układzie rombowym pierwsza pozycja w symbolu odpowiada osi krystalograficznej X, druga - osi
krystalograficznej Y, trzecia - osi krystalograficznej Z.
4. W układzie tetragonalnym pierwsza pozycja w symbolu odpowiada osi Z, druga - osiom X i Y, a trzecia -
kierunkowi [110] leżącym w płaszczyźnie XY.
5. W układzie regularnym pierwsza pozycja w symbolu odpowiada osiom krystalograficznym X,Y, Z, druga -
kierunkowi [111], a trzecia - kierunkowi [110]. W układzie tym zawsze na drugim miejscu w symbolu jest 3 lub
3 .
6. W układzie heksagonalnym i trygonalnym pierwsza pozycja w symbolu związana jest z osią Z, druga z osiami
X, Y, U, a trzecia z kierunkami połowiącymi kąty między dodatnimi i ujemnymi kierunkami osi X, Y, U.
Jeśli w danym kierunku w krysztale występuje oś symetrii n-krotna i prostopadła do niej płaszczyzna symetrii, to
zapisujemy to jako n/m. W symbolice uproszczonej we wszystkich układach, z wyjątkiem jednoskośnego,
symbol n/m zastępuje się symbolem m.
15
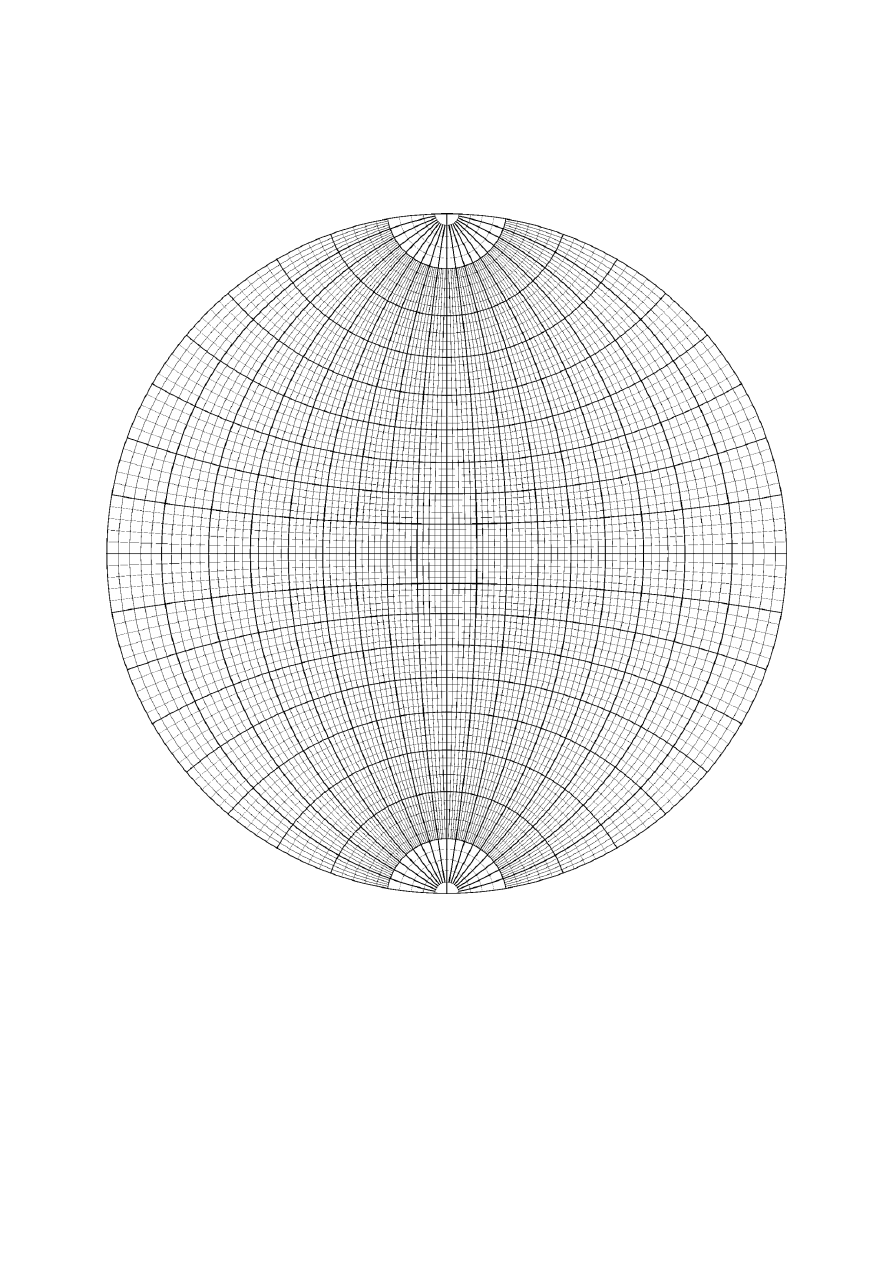
Siatka Wulfa
16
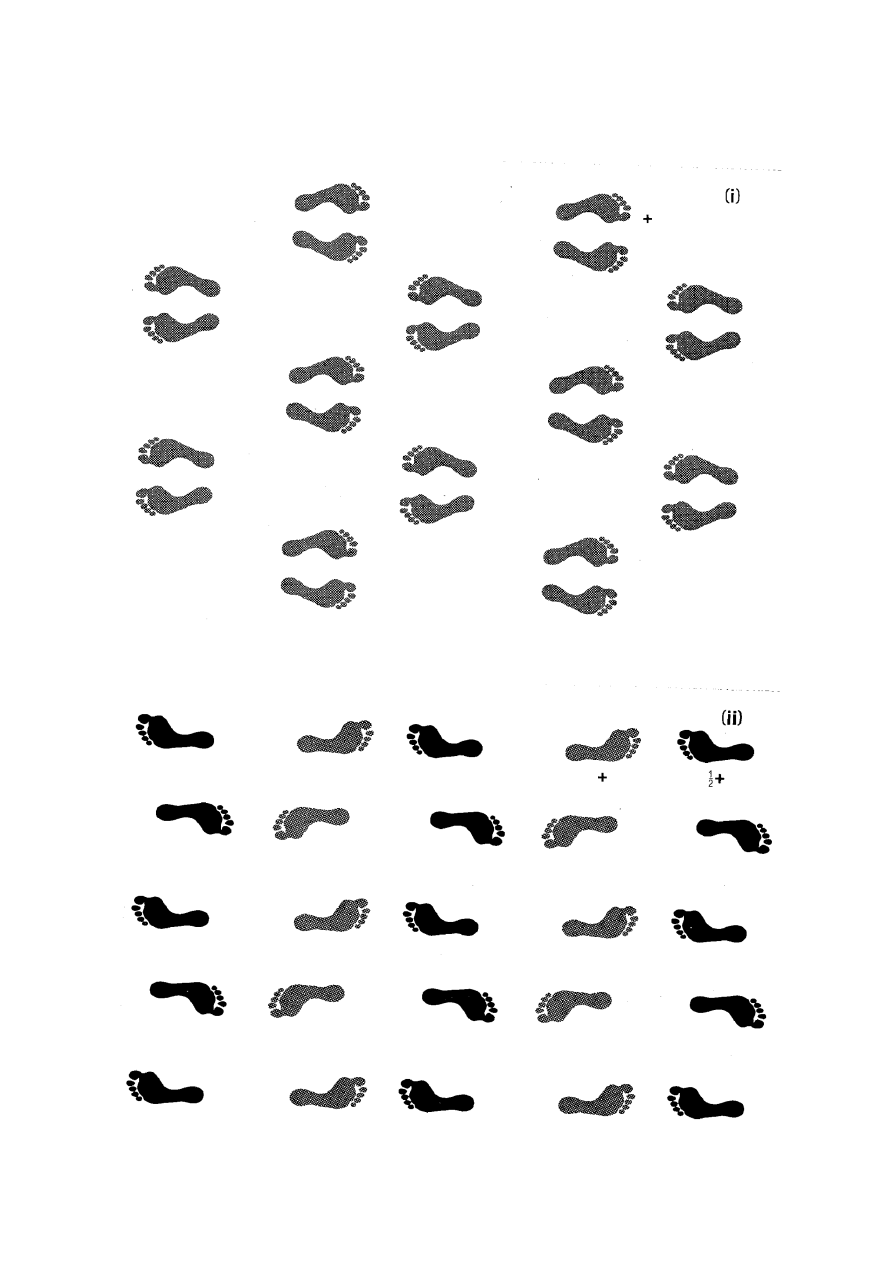
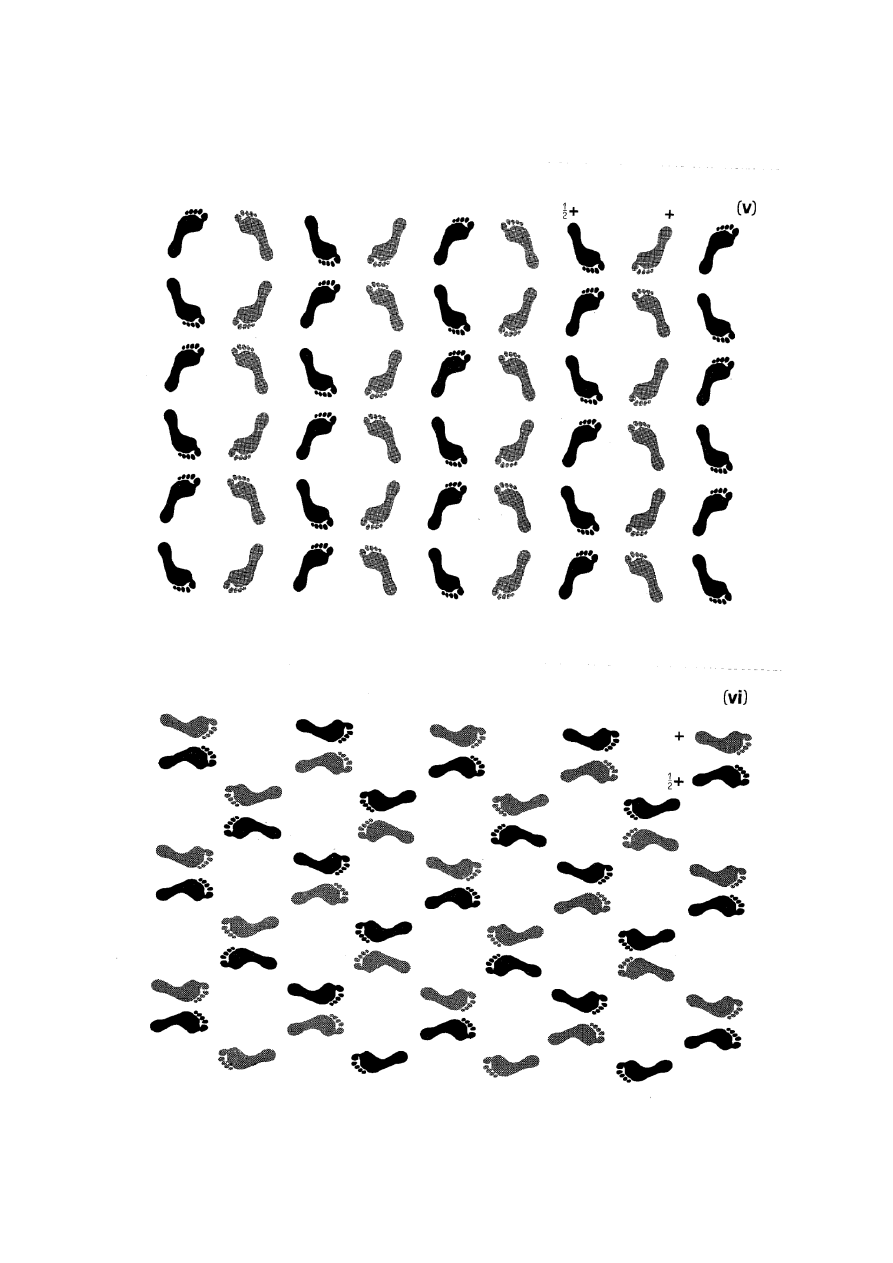
Rysunki (i) – (vx) (ćwiczenie 4, zadanie 1).
.

17
18

19

20

21

22

23
25

26

27

28

29

30

31

32

33

34

35

36
Wyszukiwarka
Podobne podstrony:
Krystalizacja, Materiały, Chemiczne, Chemia organiczna
mds materialy 2009, POZYCJE PEDAGOGICZNE
Materiałoznawstwo 2009 plus, Materiałoznawstwo egzamin
Oddziaływanie z materią 2009
Układy krystalograficzne, Materiały z Ostrowa
materiały magnetycznie, sebus, Tematem kolejnego seminarium CMZiN były krystaliczne materiay magnety
2 Stany skupienia materii 2009
2 Materiałoznawstwo mechatronika krystalografia
11.02 Siwiec-Barcik - Niewydolność oddechowa, MEDYCZNE -materiały z kursów, PACJENT WENTYLOWANY MECH
teorie socjalizacji -material uzupelniajacy z zajec 16.05.2009, socjologia, soc małych gr i rodziny
Wstepniaki- pytania- 2009-2010uzupełnione z roku 2012 umlub, materialy farmacja, I rok, biofizyka
Ćw 5 - Badanie pętli histerezy magnetycznej ferromagnetyków 2009, Politechnika Poznańska, Elektrotec
Oczyszczanie Gazow Odlotowych, Ochrona Środowiska studia, 4 rok (2009-2010), Semestr VII (Rok 4), Oc
2 Patomorfologia kolo 4 2009, IV rok Lekarski CM UMK, Patomorfologia, 3 rok - materiały, Kolokwia, K
podatki w rachunkowości, Materialy do wykladu - VAT w rachunkowosci 2009 rok, Szkoła Główna Handlowa
Krystaliczna skruktura metali, Księgozbiór, Studia, Materiałoznastwo
więcej podobnych podstron
