I

r

ok I sem budownictwo

Rok akademicki

2007/2008

Cwiczen

i

e nr

1

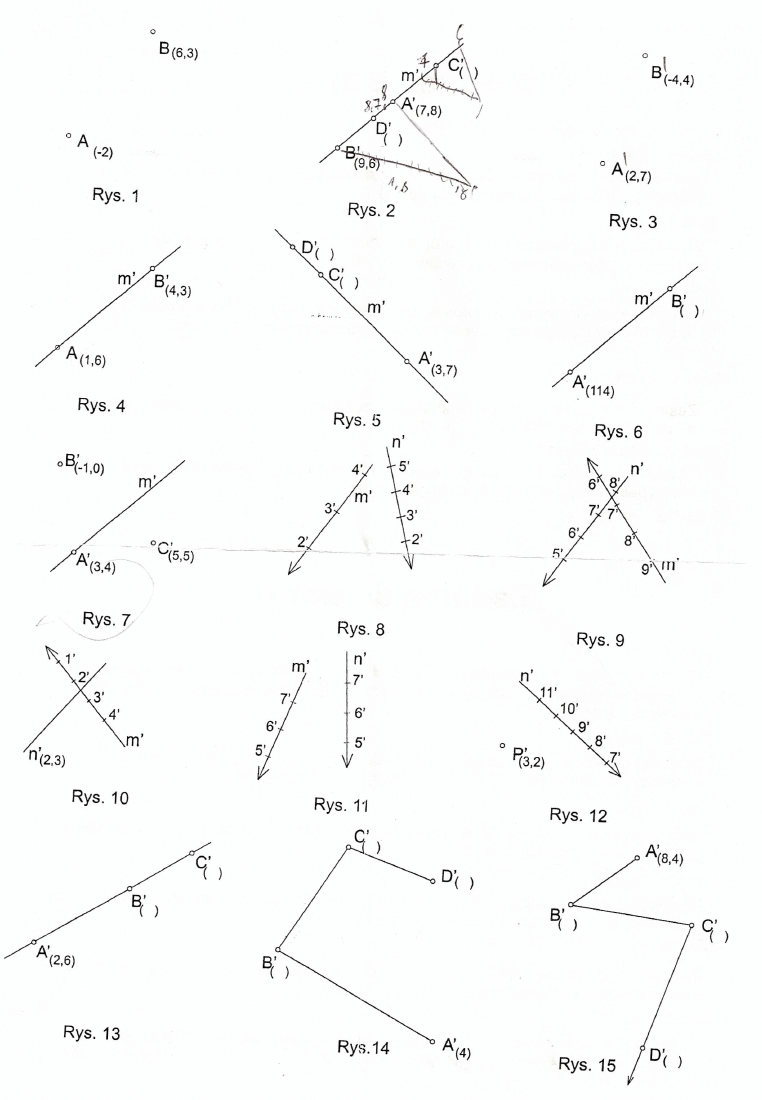
lad. 1

rys.1

Wykresli6 zestopniowany

rzut pro

.

stej

m

przechodzqcej

przez dane punkty

~

-

2/

B(6

,

3)

a nast~pnie jej modut i kqt nachylenia do rzutni.

lad.2

rys.2

Wykresli6 zestopniowany

rzut prostej

m

przechodzqcej

przez dane punkty

A

i B

a nast~pnie wyzna!Yz:j6 cech~ punkt6w

C

i

D

prostej

m.

(7.8)

(9

.

6)

lad. 3

rys.3

,

)

Wykresli6 zestopniowany

rzut prostej

m

przechodzqcej

przez dane

~y

nkty

~(2

.

7)

i

B(-4,4)

a nast~pnie wyznaczy6

rzut i cech~ punktu

C dzielacego

odcinek

J

:

!!

#

w stosunk

u

2 : 3,4

--

-==

-

'

lad. 1

rys.7

Zestopniowa6

prostq

m

przechodzqcq

przez punkt

A

(-34)

i przecinajqcq

danq prostq

n

wyznaczonq

punktami

B

(

_1

.

0)i

C(6

,

3)

.

Zad.2

rys.8,9,10,11

Zbadac czy proste

m

i

n

przecinajq si~, oraz wyznaczyc

cech~ ich punktu przeci~cia -

w przypadku gdy Sq to proste przecinajqce

si~

.

lad

.

3

rys.12

Poprowadzic

przez punkt

I;'-

<?\

prostq

m

r6wnolegtq do prostej

n.

\

.

.

,,

-

,

Zad

ania d

omow

e

lad.4

rys.4

Dana jest prosta

m

wyznaczona

punktami

A(

_

1

6)

i

B

(4.3);

zestopniowa6

prostq

m ,

a nast~pnie wyznaczyc

cechowany

rzut prostej

n'

symetrycznej

do prostej

m

wzgl~dem

rzutni.

lad.5

rys.5

Dany jest punkt

A(3

,

7)przez

kt6ry przechodzi

prosta

m

posiadajqca

nachylenie

2 : 9 ;

wyznaczy6

cechy punkt6w

C i D

nalezqcych

do prostej

m.

lad.6

rys.6

Wyznaczyc

cech~ punktu

B

w przypadku, !Jdy prosta

m

przechodzi

przez punkty

A

i

B

posiada nachylenie

15 ~

-

Zad.7

rys

.

13

Wyznaczy6 cech~ punkt6w

B

i

C

w przypadku, gdy prosta

m przechodzqca

przez

punkty

A, B

i

C

posiada nachylenie

1:

7

.

lad

.

6

rys.14

Zestopniowac

odcinki

AB,

BC

i

C

D

tak, by ich spadek byt staty

i

wynosH

2

: 15

.

Nalezy r6wniez wyznaczyc

cechy punkt6w

B

,

C

,

D

.

lad.7

rys.15

Wyznaczy6 zestopniowany

rzut cechowany tamanej trasy odcinkowej

AB

, B

C

, CD

w przypadku, gdy punkt koncowy posiada cech~

A

zas nachylenie jest state i wynosi

15° / lub 1 :

1

0/

.

.

(8,4)

A'(2,6)

RY~A

'

(4J

o

l

8(-4,4)

o

A

'

(2,7)

Fi'

-

/

-

11'

10'

9'

8

'

o

~3

,

2)

7

'