53
Artur DUCHACZEK
1
Zbigniew MAŃKO
2
OCENA TRWAŁOŚCI EKSPLOATACYJNEJ
DŹWIGARÓW STALOWYCH MOSTÓW NISKOWODNYCH
W pracy przedstawiono sposób określania pozostałej trwałości eksploatacyjnej dźwigarów stalowych mostów
niskowodnych w przypadku stwierdzenia w nich pęknięć zmęczeniowych. Przedstawiona funkcja charakteryzująca
geometrię elementu (współczynnik kształtu Y) dla wybranego przypadku uszkodzenia dźwigarów stalowych
umożliwia w stosunkowo prosty sposób szacowanie trwałości eksploatacyjnej. Podano również pewne
ograniczenia w stosowaniu kryterium siłowego w celu dokonania oceny trwałości eksploatacyjnej mostów
wojskowych (lub objazdowych) wykonanych z kształtowników stalowych.
1. Wstęp
W większości obiektów mostowych w trakcie ich wieloletniej eksploatacji występują pęknięcia
zmęczeniowe. Umiejętność określania trwałości konstrukcji z występującym pęknięciem zmęczenio-
wym wydaje się z ekonomicznego punktu widzenia bardzo ważne. Dopuszczenie takich konstrukcji do
eksploatacji poprzez podanie dopuszczalnego okresu ich eksploatacji lub poprzez określenie
bezpiecznego obciążenia jest bardzo praktyczne.
Od wielu lat prowadzone są badania umożliwiające szacowanie trwałości konstrukcji mostowych
z występującą szczeliną zmęczeniową. Konstruktorom w rozwiązywaniu tego problemu z pomocą
przychodzą nowe gałęzie nauki, jak np. mechanika pękania. A. Neimitz w pracy [1] przedstawił
podstawowe zadania stojące przed tą dyscypliną nauki wskazując, iż dostarcza ona narzędzi
umożliwiających właściwe obliczenie wytrzymałości konstrukcji zawierającej defekty typu mikropę-
knięcie o określonej wielkości.
W pracy skoncentrowano się na konstrukcjach stalowych mostów niskowodnych, przy ocenie
pozostającej trwałości eksploatacyjnej, w której próbuje się wykorzystać osiągnięcia mechaniki
pękania. Autorzy prac [2], [3], [4] korzystają przede wszystkim z kryterium wytrzymałościowego
(siłowego), opartego na współczynniku intensywności naprężeń. Kryterium to może być jednak
wykorzystywane tylko w przypadku pękania kruchego w warunkach płaskiego stanu odkształcenia.
W pracy przedstawiono również pewne ograniczenia w stosowaniu kryterium siłowego w określaniu
pozostałej trwałości eksploatacyjnej stalowych mostów wojskowych.
2. Eksploatacja stalowych przęseł mostowych ze szczeliną zmęczeniową
Podstawowymi parametrami niezbędnymi do prowadzenia obliczeń prędkości rozwoju pęknięć
zmęczeniowych są różnego rodzaju współczynniki empiryczne wykorzystywane do opisu kinema-
tycznego wykresu pękania zmęczeniowego. M. Szata w pracy [5] przedstawił szeroką gamę wzorów
1
Kpt. mgr inż., Wyższa Szkoła Oficerska Wojsk Lądowych im. gen. T. Kościuszki we Wrocławiu
2
Dr hab. inż., prof. PWr., Instytut Inżynierii Lądowej Politechniki Wrocławskiej
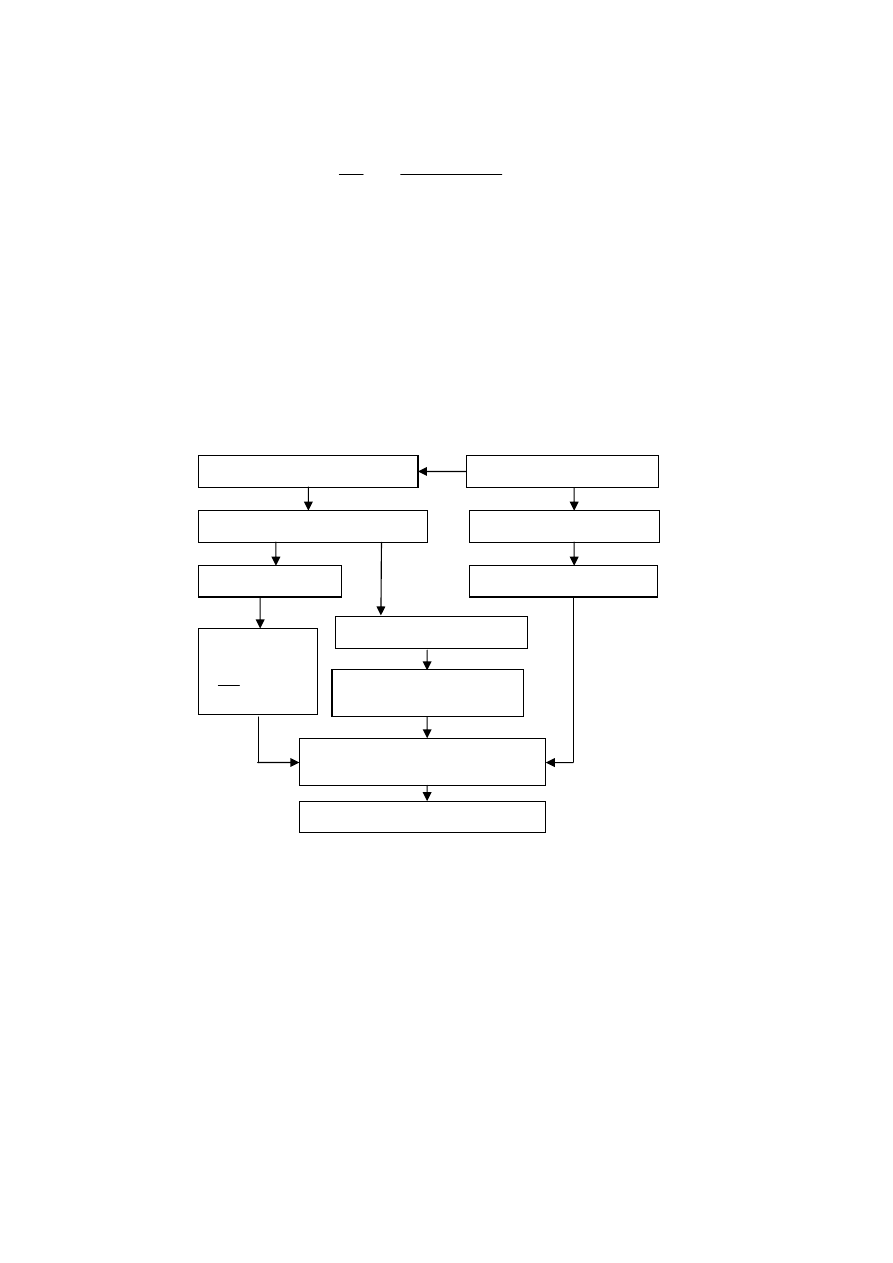
54
opisujących prędkość wzrostu szczelin zmęczeniowych. Dla praktyki inżynierskiej najbardziej
praktyczne będą jednak wzory o minimalnej liczbie stałych materiałowych. Zdaniem autorów pracy
takim rozwiązaniem może być wzór (1) zaproponowany przez R. G. Formana [1], [5]:
K
K
R
K
C
N
a
m
∆
−
−
∆
=
c
F
1
F
)
(
)
(
d
d
(1)
Stałe materiałowe m
F
i C
F
wyznacza się z danych doświadczalnych. Wielkość K
c
oznacza
odporność na pękanie w konkretnych warunkach obciążenia. Zakres zmienności współczynnika
intensywności naprężeń
∆K, to czynnik decydujący o prędkości propagacji szczeliny. Zaletą tego
rozwiązania jest fakt, że opisuje on dwie fazy (II i III) kinematycznego wykresu pękania
zmęczeniowego i jednocześnie uwzględnia wpływ asymetrii cyklu obciążenia R wpływającego na
wzrost szczeliny zmęczeniowej [6].
Aktualna wiedza dotycząca rozwoju pęknięć zmęczeniowych konstrukcji stalowych coraz częściej
zachęca do wykorzystania jej podczas szacowania pozostałej trwałości eksploatacyjnej obiektów
mostowych. Prób takich w swych pracach dokonali m.in. B. Wichtowski i K. Rykaluk [3] oraz
K. Sturzbecher [4]. Od paru lat w WSOWLąd. we Wrocławiu prowadzone są badania dotyczące
zastosowania podstawowych praw mechaniki pękania przy ocenie pozostającej trwałości
eksploatacyjnej stalowych mostów wojskowych.
Rys. 1. Algorytm oszacowania trwałości zmęczeniowej konstrukcji przęseł ze szczeliną zmęczeniową
Mimo, iż z założenia mosty niskowodne to konstrukcje tymczasowe, dość często są one
wykorzystywane przez ludność cywilną jako obiekty na trwałe wpisane w sieć dróg lokalnych
(szczególnie na terenach bardzo mało zurbanizowanych, wiejskich lub objazdowych, itp.). Wydaje się
zatem oczywiste, że istnieje potrzeba stworzenia metody umożliwiającej w dość prosty sposób
oszacowanie trwałości takiego obiektu. Analizując istniejący stan wiedzy i praktyczne przykłady
wykorzystania zasad mechaniki pękania we współczesnych problemach wytrzymałościowych
w oparciu o pracę [7] zaprezentowano algorytm prowadzenia takich analiz (rys. 1).
Algorytm przedstawiony na rys. 1 wykorzystano w pracy [8]. Głównym celem tej pracy było
przedstawienie koncepcji określania rezerw trwałości zmęczeniowej mostów wojskowych, czyli
określenie jak długo (w sensie czasowym) lub ile cykli obciążeń o znanych parametrach można jeszcze
bezpiecznie dopuścić na eksploatowany most (w zależności od klasy obciążenia), po stwierdzeniu
powstania pęknięcia w dźwigarach stalowych o znanej wielkości (długości).
Jakość i wiarygodność przeprowadzonych obliczeń uzależniona była m.in. od dostępu do wzorów
umożliwiających obliczenie współczynnika intensywności naprężeń. W pracy [1] podano źródła
Widmo kumulacyjne
Konstrukcja przęsła
Obciążenie eksploatacyjne
Element konstrukcji
Przebieg obciążeń
Wykres
)
( K
f
N
a
∆
=
d
d
Materiał
Szczegóły konstrukcyjne
Początkowa lokalizacja
i geometria pęknięcia
Analiza rozwoju pęknięć
(np. wzór Formana)
Ocena trwałości zmęczeniowej
55
(m.in. [9] i [10]) umożliwiające wykorzystanie dość dużej liczby gotowych rozwiązań. W praktyce
inżynierskiej jednak nie ma możliwości rozpatrzenia wszystkich występujących przypadków obciążeń.
Aktualnie istnieją różnorakie metody umożliwiające rozwiązanie tego problemu, m.in. A. Nemitz
w pracy [1] przedstawił dość szeroką ich gamę.
Wydaje się, że najbardziej uniwersalnym narzędziem dla współczesnych projektantów będą jednak
sposoby wyznaczania współczynnika intensywności naprężeń oparte na metodzie elementów skończo-
nych (MES), szczególnie, że aktualnie dostępność na rynku oprogramowania umożliwiającego wykona-
nie takich obliczeń jest bardzo duża.
W pracach [1] i [11] przedstawiono metodę wykorzystania wyników obliczeń wytrzymałościowych
przeprowadzonych przy wykorzystaniu oprogramowania opartego na MES do obliczania współ-
czynnika intensywności naprężeń.
Nie wszyscy naukowcy zajmujący się problematyką rozwoju pęknięć zmęczeniowych
w konstrukcjach stalowych są zwolennikami metody opartej na określeniu współczynnika
intensywności naprężeń. Do nich zalicza się m.in. M Szata, który w pracy [5] uwypukla wady
przedstawionej powyżej metody, proponując w zamian opis rozwoju zmęczeniowego pękania w ujęciu
energetycznym. W literaturze przedmiotu brak jest jednak wystarczającej liczby przykładów
praktycznego wykorzystania tego sposobu rozwiązania.
3. Ograniczenia w stosowaniu kryterium siłowego do oceny pozostałej trwałości zmęczeniowej
A. Nemitz w pracy [1] przedstawił sposoby zastosowania mechaniki pękania w praktycznych
zagadnieniach inżynierskich, poświęcając jeden z rozdziałów pękaniu kruchemu w warunkach
płaskiego stanu odkształcenia. Jednym z powodów, dla którego coraz częściej tę grupę zagadnień
próbuje się wykorzystywać przy określaniu pozostałej trwałości eksploatacyjnej mostów stalowych jest
na pewno fakt, iż pomiar odporności na pękanie K
Ic
w płaskim stanie odkształcenia jest stosunkowo
łatwy i dość jednoznaczny.
Jeśli pękanie znajduje się w elemencie o dużej grubości, to stwierdzono, że występuje w nim płaski
stan odkształceń. W takim przypadku rozwój odkształceń plastycznych jest ograniczony poprzez stan
naprężeń modyfikowany wymiarami próbki, i proces pękania w przeważającej części ma kruchy
charakter [1].
Fakt, że kształt i wielkość strefy plastycznej wzdłuż frontu pęknięcia zmienia się, ma duże
znaczenie zarówno w procesie modelowania szczeliny jak i zjawisk zachodzących blisko jej
wierzchołka. Wpływa to bezpośrednio na model ciała, jaki należy przyjąć do obliczeń. Według
A. Nemitza [1] przy bardzo małej strefie plastyczności, gdy:
a
,
r
01
0
p
≤
(2)
gdzie: r
p
– promień strefy plastycznej, a – długość szczeliny, można z powodzeniem stosować teorię
liniowej mechaniki pękania. Jednocześnie przy spełnieniu warunku (2) uznaje się, że obszar plastyczny
jest całkowicie kontrolowany przez otaczający go obszar sprężysty.
Długość strefy plastycznej można określić za pomocą jednego z uproszczonych wzorów. Dla płaskiego
stanu odkształcenia można zastosować wzór wynikający z modelu Irwina w postaci (3) [1]:
2
e
I
p
6
1
=
R
K
r
π
(3)
w którym K
I
jest współczynnikiem intensywności naprężeń zależnym od geometrii ciała, długości
i kształtu szczeliny oraz przyłożonego do niego obciążenia, a R
e
jest granicą plastyczności.
Istota kryterium siłowego, które jest też kryterium lokalnym, polega na stwierdzeniu, że choć
naprężenia są osobliwe w wierzchołku szczeliny, to jednak wielkość (amplituda) tej osobliwości
określana przez współczynnik intensywności naprężeń jest wielkością skończoną [1]. Siłowe kryterium
pękania, bądź też kryterium krytycznego współczynnika intensywności naprężeń, może być
przedstawione wzorem (4) [6]:
Ic
I
K
K
=
(4)
gdzie K
Ic
jest parametrem materiałowym wyznaczanym eksperymentalnie (odporność na kruche pękanie).
56
Korzystając z wyrażenia (4) można bezpośrednio wyznaczyć obciążenie krytyczne przy znanych,
innych wielkościach występujących w K
I
, bądź alternatywnie określić długość krytyczną szczeliny przy
znanym obciążeniu i pozostałych parametrach geometrycznych ciała.
K
Ic
K
grubość elementu
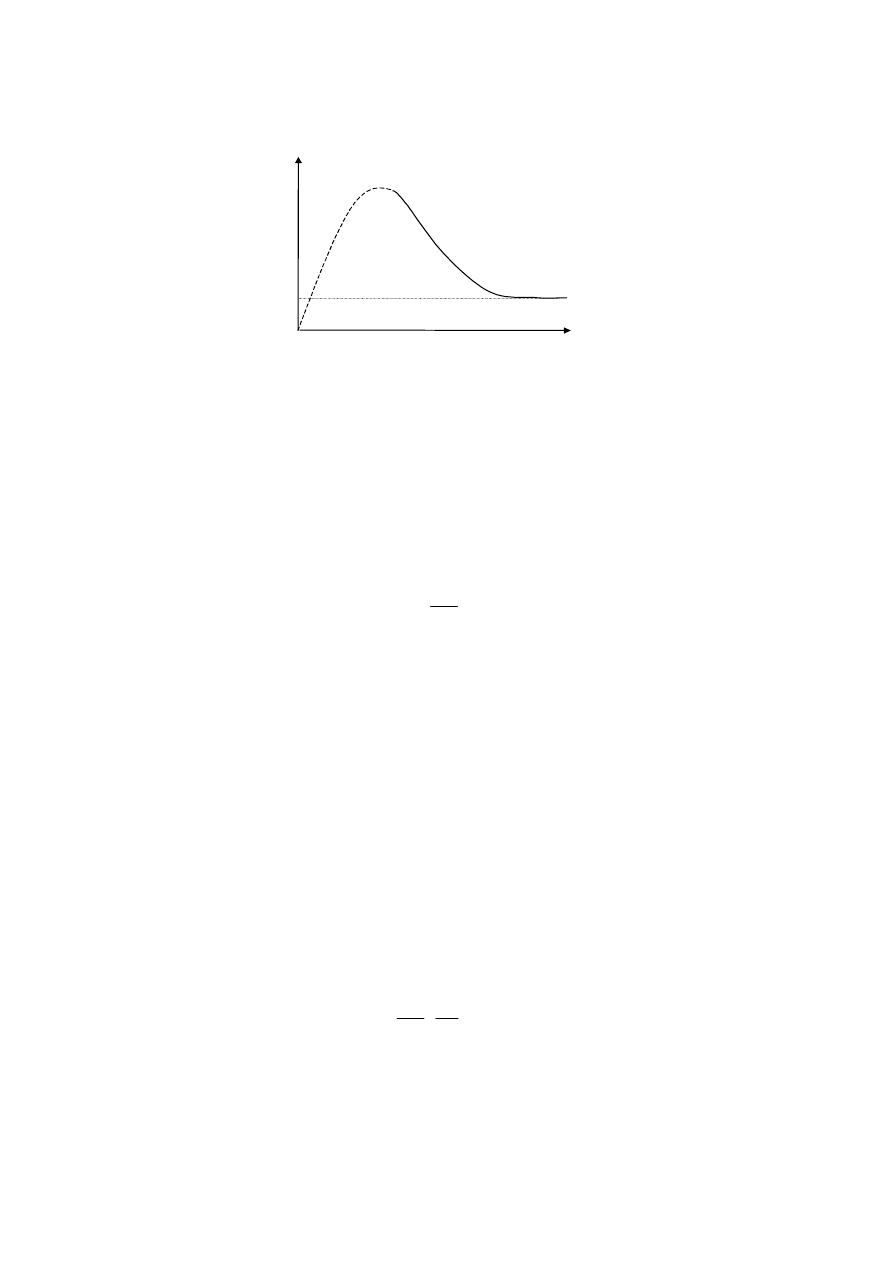
Rys. 2. Wpływ grubości elementu na wielkość współczynnika intensywności naprężeń [6]
S. Kocańda i J. Szala w pracy [12] podają, że współczynnik intensywności naprężeń K zależy
w istotny sposób od grubości elementu (rys. 2). Jednak od określonej dla danego materiału grubości,
współczynnik intensywności naprężeń K nie zmienia się. Tę właśnie wartość współczynnika
intensywności naprężeń K
I
dla danego materiału przyjęto jako odporność na pękanie K
Ic
.
Niezależność współczynnika K
Ic
od geometrii jest niezwykle ważna, jeżeli wielkość zmierzoną na
próbkach w laboratorium w sytuacji wyidealizowanej zamierza się wykorzystać w praktyce
inżynierskiej dla dowolnej wielkości elementu konstrukcyjnego zawierającego szczelinę.
A. Neimitz [1] podaje, że powyżej grubości próbki B, określonej wzorem (5), krytyczna wartość
współczynnika intensywności naprężeń K
I
pozostaje niezmienna:
2
e
Ic
5
,
2
≥
R
K
B
(5)
gdzie K
Ic
jest odpornością na kruche pękanie, a R
e
granicą plastyczności.
Spełnienie warunku opisanego wzorem (5) w praktyce inżynierskiej może spowodować znaczne
ograniczenia, co do możliwości wykorzystania kryterium siłowego.
Autorzy pracy zajmują się określaniem pozostałej trwałości eksploatacyjnej stalowych mostów
wojskowych. Podstawowym elementem konstrukcyjnym w tych obiektach są kształtowniki stalowe,
a wśród nich przede wszystkim dwuteowniki i ceowniki. Wymiary kształtowników są w znacznym
stopniu znormalizowane (chociażby ofertą handlową producentów). Elementami, które znajdują się
w obszarze zainteresowania i rozważań są środniki i pasy tych kształtowników.
Reasumując wywody przedstawione w pracach [1], [6] i [12] można postawić konkluzje, że:
1. Spełnienie równania (1) jest warunkiem koniecznym, aby można było stosować prawa liniowej
mechaniki pękania, gdyż w tym przypadku uważa się, że obszar plastyczny jest całkowicie
kontrolowany przez otaczający go obszar sprężysty.
2. Spełnienie warunku opisanego równaniem (4) jest konieczne, aby proces pękania odbywał się
w płaskim stanie odkształcenia, i w tych warunkach K
Ic
staje się stałą materiałową.
Po przekształceniu wzorów (2) i (3) otrzymuje się równanie (6) na minimalną długość szczeliny
w zależności od wartości współczynnika intensywności naprężeń K
I
, przy której zostaje spełnione
równanie (2).
2
e
I
π
6
100
≥
R
K
a
(6)
Stwierdzono, że dla określonego gatunku stali nie można określić minimalnych i maksymalnych
wymiarów szczeliny, dla których spełniony jest warunek (2). Każdorazowo, osobno dla każdego
przypadku, należy obliczać wartość współczynnika intensywności naprężeń, gdyż to od jego wartości
bezpośrednio zależy wartość minimalnej długości szczeliny, dla której można stosować równania
liniowej mechaniki pękania.
57
Wartość współczynnika intensywności naprężeń oblicza się ze wzoru (7):
a
Y
K
π
σ
=
(7)
w którym Y jest współczynnikiem (liczbowym lub funkcyjnym) związanym ze skończonymi
wymiarami ciała, a σ oznacza naprężenia od przyłożonego obciążenia, natomiast a jest aktualną
długością szczeliny.
Podstawiając równanie (7) do wzoru (6) otrzymuje się w przybliżeniu wyrażenie (8):
Y
R
e
25
,
0
≤
σ
(8)
Równanie (8) umożliwia określenie maksymalnych wartości naprężeń w rozpatrywanym elemencie
konstrukcyjnym, które zapewniają spełnienie warunku (2). Niestety w równaniu tym nie udało się
również ominąć każdorazowego wykonywania obliczeń. Współczynnik kształtu Y jest dla zdecydowajej
większości przypadków wielkością bezpośrednio uzależnioną od aktualnych wymiarów szczeliny a.
Wartości współczynnika kształtu Y mogą przyjmować zarówno wartości większe jak i mniejsze
od jedności. Dla przypadków dotychczas analizowanych w pracy [8] przyjęcie wartości współczynnika
kształtu Y zbliżonej do 1,2 jest rozwiązaniem wystarczająco konserwatywnym (z dużym
współczynnikiem bezpieczeństwa).
Po podstawieniu wartości Y = 1,2 do równania (8) otrzymuje się równanie (9):
e
21
,
0
R
≤
σ
(9)
Równanie to uzależnia maksymalne naprężenia panujące w elemencie konstrukcyjnym, w którym
analizuje się rozwój pęknięcia, jedynie od wartości granicy plastyczności. Tak przedstawiona zależność
umożliwia błyskawiczne oszacowanie możliwości spełnienia równania (2), które stanowi podstawowy
warunek prowadzenia dalszych obliczeń zmęczeniowych.
Przedstawiony wzór (9) jest zależnością bardzo restrykcyjną. S. Kocańda i J. Szala [12] podają,
że jeżeli naprężenia nominalne σ ≤ 0,4 R
e
to uwzględnienie strefy plastycznej przy obliczeniach
współczynnika intensywności naprężeń nie jest konieczne, gdyż błąd wywołany przyjęciem modelu ciała
doskonale sprężystego do obliczenia współczynnika intensywności naprężeń K nie przekracza 5%.
Przy projektowaniu stalowych przęseł mostów niskowodnych obliczenia wytrzymałościowe
wykonuje się dla skrajnego, najbardziej obciążonego dźwigara głównego, określając naprężenia
w połowie jego rozpiętości teoretycznej. Mając na uwadze, że w obszarze tym nie należy wykonywać
żadnych połączeń, które osłabiałyby jego przekrój (np. połączenia na śruby), można przyjąć,
że w miejscach powstania rzeczywistych uszkodzeń (tj. pęknięć inicjujących się z otworów
montażowych) będą panowały naprężenia znacznie mniejsze od maksymalnych obliczonych w przęśle.
Z przedstawionych w pracy [8] analiz wynika, że w przypadku konstrukcji mostów niskowodnych
istnieją bardzo duże przesłanki do spełnienia równania (2), a co za tym idzie możliwości wykorzystania
równań liniowej teorii sprężystości.
J. German w pracy [6] podaje, iż liniowa mechanika pękania może być stosowana dla materiałów,
dla których stosunek modułu sprężystości E do granicy plastyczności R
e
jest mniejszy od 200–250.
Wynika to z faktu, iż w tym przedziale podstawowa charakterystyka materiałowa, jaką się
ona posługuje tzn. K
Ic
nie zależy od wymiarów próbki. Ponieważ dla stali gatunków St3M i 18G2A
podany w pracy [6] warunek nie jest spełniony, należy wówczas przeanalizować wymiary
podstawowych kształtowników stalowych używanych do budowy mostów niskowodnych.
Obliczone według wzoru (5) grubości próbek B (tj. 180 mm dla stali St3M i 110 mm dla 18G2A)
z punktu widzenia praktycznego są nie do przyjęcia, gdyż w rzeczywistych warunkach nie występują
kształtowniki stalowe, które miałyby tak grube środniki i półki. Nie istniałaby, zatem możliwość
pobrania wiarygodnych próbek z tych elementów.
A. Neimitz w przypadku niespełnienia warunku (5) dopuszcza określenie wartości K
Ic
na podstawie
równania (10), gdyż warunki dotyczące minimalnych wymiarów próbek B są wówczas mniej
restrykcyjne. Należy mieć jednak na uwadze, że tak naprawdę wielkość K
Ic
przestaje wówczas
obowiązywać, gdyż grubość elementu konstrukcyjnego nie spełnia warunku (5):
58
)
1
(
2
Ic
Ic
ν
−
=
E
J
K
(10)
gdzie: J
Ic
– krytyczna wartość całki J, ν – współczynnik Poissona, E – moduł Younga.
W przypadku dwuteowników stalowych grubość środników (lub pasów) będzie mniejsza od wyma-
ganej równaniem (5). Biorąc jednak pod uwagę wykres przedstawiony na rys. 2 można spodziewać się,
że rzeczywista dopuszczalna wartość współczynnika intensywności naprężeń w dwuteownikach
stalowych przekroczy wartość K
Ic
obliczoną w warunkach płaskiego stanu odkształcenia, przez co
wyniki obliczeń zmęczeniowych będą po stronie bezpiecznej, tj. ze znacznym zapasem bezpieczeństwa.
4. Rozwój pęknięć zmęczeniowych w połączeniach montażowych dźwigarów stalowych
W przypadku przęseł mostów niskowodnych wykonanych z dwuteowników stalowych, projektan-
towi, oprócz obliczeń wytrzymałościowych elementu zasadniczego, jakim jest dźwigar główny
wykonany z kształtownika stalowego, pozostaje problem ich połączenia ze stężeniami poprzecznymi
wykonanymi zazwyczaj również z dwuteowników stalowych oraz specjalnych blach węzłowych [13].
W 2001 roku w WSOWLąd. we Wrocławiu zespół pod kierownictwem Z. Mańko i Z. Kamyka
w ramach projektu badawczego [13] zaprojektował przęsło mostu niskowodnego przeznaczone
pod obciążenie MLC70, w którym do połączenia stężeń poprzecznych użyto śrub.
Proponowany sposób montażu stężeń poprzecznych wymagał wykonania w dźwigarze głównym
w kilku miejscach (w zależności od liczby stężeń) minimum czterech otworów.
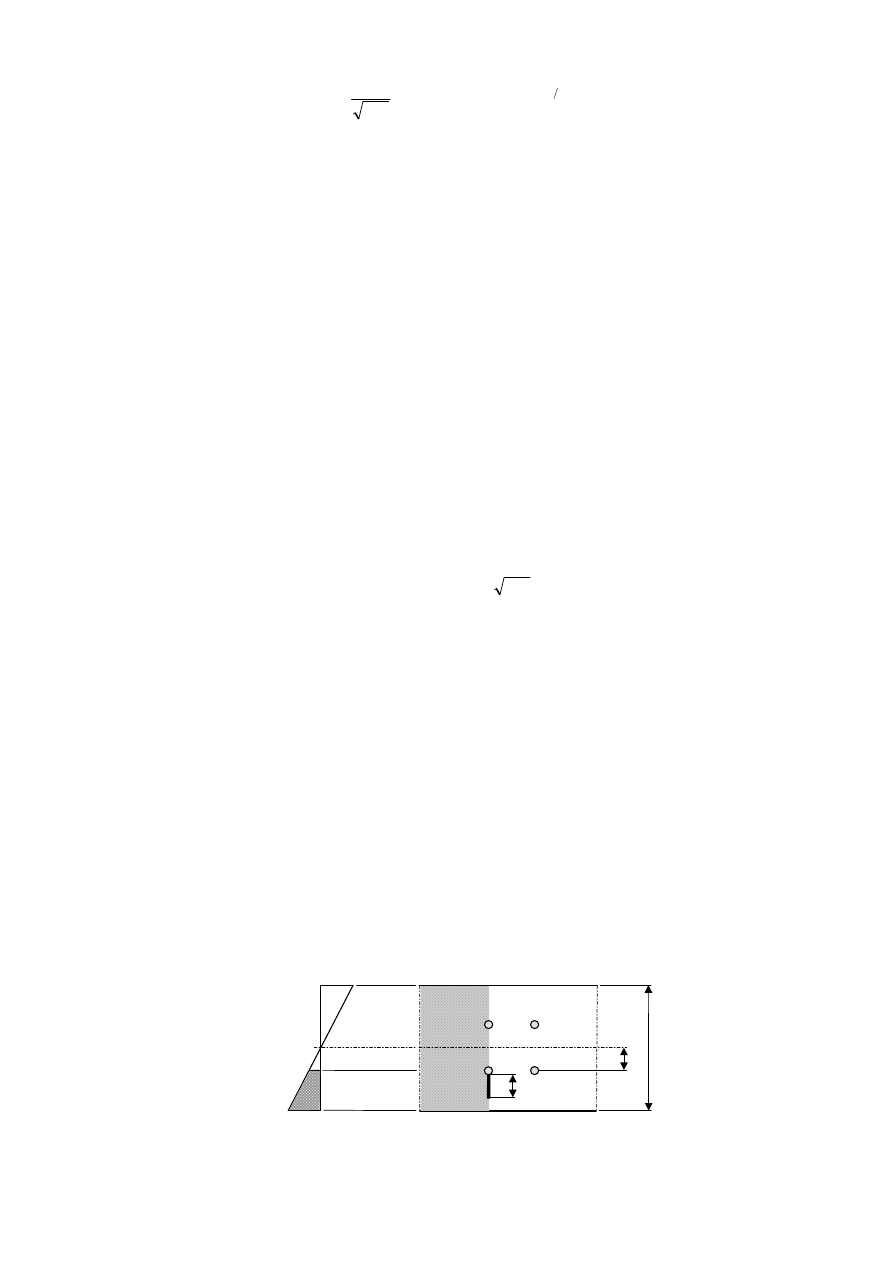
Rys. 3. Wpływ otworów montażowych w strefie rozciąganej dźwigara głównego na rozkład naprężeń normalnych
Otwory występujące w strefie rozciąganej dźwigara głównego osłabiają jego konstrukcję
i jednocześnie stanowią potencjalne miejsce kumulacji naprężeń, a w przyszłości miejsce inicjacji
pęknięcia (rys. 3).
Sposób wykonania połączenia uniemożliwia zaobserwowanie pęknięcia o minimalnych wymiarach.
W zależności od wymiarów blachy węzłowej użytej do konstrukcji stężeń poprzecznych wymiary
szczeliny mogą wynosić nawet kilkadziesiąt milimetrów. Duże wymiary pęknięcia w stosunku
do wielkości strefy plastycznej mogą umożliwić wykorzystanie podstawowych zależności znanych
z liniowej mechaniki pękania do analizy prędkości rozwoju istniejącego pęknięcia. Należy mieć jednak
na uwadze ograniczenia w wykorzystaniu wielkości odporności na pękanie K
Ic
, wynikające przede
wszystkim z niewielkich grubości stosowanych środników w kształtowników stalowych.
W pracy wykorzystano wyniki przeprowadzonych komputerowo obliczeń pola naprężeń wokół
pęknięcia. Elementy przylegające do pęknięcia zostały zmodyfikowane tak, aby obliczenia w tym
miejscu oddawały osobliwość pola naprężeń znaną z rozwiązań analitycznych [11].
Obliczenia metodą elementów skończonych przeprowadzono tylko dla serii pęknięć o ustalonej
głębokości. Przyjęty model obliczeniowy (numeryczny) nie umożliwiał jawnego wzrostu pęknięcia.
Założono, że do symulacji wzrostu pęknięcia zmęczeniowego wykorzystane zostanie podejście
analityczne. W zakresie obliczeń analitycznych historii wzrostu pęknięcia możliwe jest szybkie
sprawdzenie wpływu różnych charakterystyk obciążenia, aż do osiągnięcia przez pęknięcie stanu
krytycznego [11]. Zasadę określania współczynnika intensywności naprężeń K, niezbędnego
do wyprowadzenia wartości funkcyjnej współczynnika kształtu Y zaprezentowano m.in. w pracach [1]
i [11]. Aby możliwa była ocena żywotności omawianych elementów, należy najpierw wyprowadzić
funkcyjny zapis na wartość współczynnika kształtu Y.
Pękanie w środniku dwuteownika stalowego zdecydowano się zbadać jako pękanie w kruchym
materiale liniowo-sprężystym, zwracając jednak uwagę na ograniczenia przedstawione powyżej.
Koniecznym było zatem zdefiniowanie parametrów kontrolujących pękanie takiego materiału.
W najogólniejszej formie rozkład naprężeń przed wierzchołkiem szczeliny można przedstawić
za pomocą wzoru (11) [1]:
59
∑
+
=
∞
=
=
−
n
n
n
n
n
n
f
r
C
f
r
K
2
)
(
ij
2
)
2
(
)
(
α
)
(
ij
α
ij
)
(
)
(
π
2
θ
θ
σ
α
α
(11)
gdzie wyrażenie f
ij
(n)α
jest uniwersalną funkcją kąta θ niezależną od geometrii próbki, ani też
od zewnętrznego obciążenia, indeksy zaś i, j = {1, 2, 3} wskazują na odpowiednią składową wielkości
tensorowej lub wektorowej w układzie współrzędnych kartezjańskich {X
i
}, zaś indeks α = I, II, III
oznacza sposób obciążenia próbki, tzw. modę, r jest odległością od wierzchołka szczeliny,
a współczynniki K
(
α)
i C
n
(
α)
zależą od geometrii próbki oraz od wielkości obciążenia zewnętrznego.
Aby określić współczynnik intensywności naprężeń można posłużyć się podejściem bezpośrednim
albo pośrednim. W przypadku podejścia bezpośredniego, K oblicza się bazując na wzorze (11)
i wyliczonym numerycznie polu naprężeń lub przemieszczeń w pobliżu szczytu pęknięcia. W podejściu
zaś pośrednim mierzy się współczynnik uwalniania energii G, co można wykonać określając stan
energetyczny całego ciała lub na podstawie całki J, a następnie oblicza się K ze wzoru obowiązującego
dla materiałów liniowo-sprężystych [11].
Współczynniki intensywności naprężeń można obliczyć bezpośrednio z przekształcenia wzoru (11),
w którym pojawia się osobliwość polegająca na uzależnieniu pierwszego z jego członów od odległości
pęknięcia poprzez wyrażenie r
(–1/2)
. Powoduje to, że w pobliżu szczytu pęknięcia naprężenia sprężyste
dążą do nieskończoności i dla ich opisu wystarcza skrócić wzór (11) o drugi człon sumacyjny. Pozwala
to na jednoznaczne określenie K w funkcji naprężeń i parametrów geometrycznych. A. Neimitz [1]
podaje, że w tym zagadnieniu za bliski obszar należy uznać punkty leżące nie dalej jak w odległości 1%
długości pęknięcia (r
p
< 0,01a) od szczytu pęknięcia. Natomiast w pracy [11] podano, że dane
otrzymane z symulacji numerycznych zebrane przez D. Broeka [14] wskazują, że obszar bliski
dla wyznaczania K
I
z inżynierską dokładnością rozciąga się na odległość około 5% długości pęknięcia
licząc od jego szczytu. W praktyce inżynierskiej należy więc określić numerycznie pole naprężeń
wokół pęknięcia i obliczyć współczynniki intensywności naprężeń ze wzoru (12) [1]:
)
π
2
(
lim
22
0
I
r
K
r
σ
→
=
(12)
przy czym obowiązuje on dla θ = 0. Z uwagi na to, że obliczenia numeryczne mają charakter dyskretny, to
granicę we wzorze (12) należy traktować umownie i naprężenia niezbędne do wyznaczania K
I
nie
powinny być wzięte z elementów skończonych bezpośrednio przyległych do powierzchni pęknięcia [11].
A. Nemitz [1] podaje, że współczynnik intensywności naprężeń oblicza się sporządzając wykres
wielkości ujęty w nawiasach wyrażenia (12) w funkcji odległości od wierzchołka szczeliny r,
a następnie ekstrapolując tę funkcję do r = 0.
Należy też zwrócić uwagę na fakt, że naprężenia uzyskane metodą elementów skończonych
są określone z mniejszą dokładnością niż pola przemieszczeń. Dlatego za dokładniejszą metodę
wyznaczania współczynnika intensywności naprężeń uważa się posługiwanie się wzorami bazującymi
na przemieszczeniach wokół pęknięcia [1].
W pracy wykorzystano metodę bezpośrednią określenia współczynników intensywności naprężeń
obliczając wartości naprężeń w pobliżu szczytu pęknięcia, tj. z definicyjnego wzoru (11)
i wynikającego z niego wzoru (12). Przyjęcie takiego rozwiązania wynikało z przyjętego schematu
obliczeniowego, który uniemożliwiał analizę przemieszczeń w wierzchołku szczeliny.
Numeryczne obliczenia w mechanice pękania są obecnie najbardziej rozpowszechnionym
narzędziem do ustalenia parametrów pęknięć występujących w zagadnieniach o nietypowej geometrii.
Badania laboratoryjne wykonuje się niemal wyłącznie na zestandaryzowanych (normowych) próbkach
w celu określenia odporności na pękanie badanego materiału, a nie rodzaju pęknięcia [11].
σ
1
W
X
σ
2
a
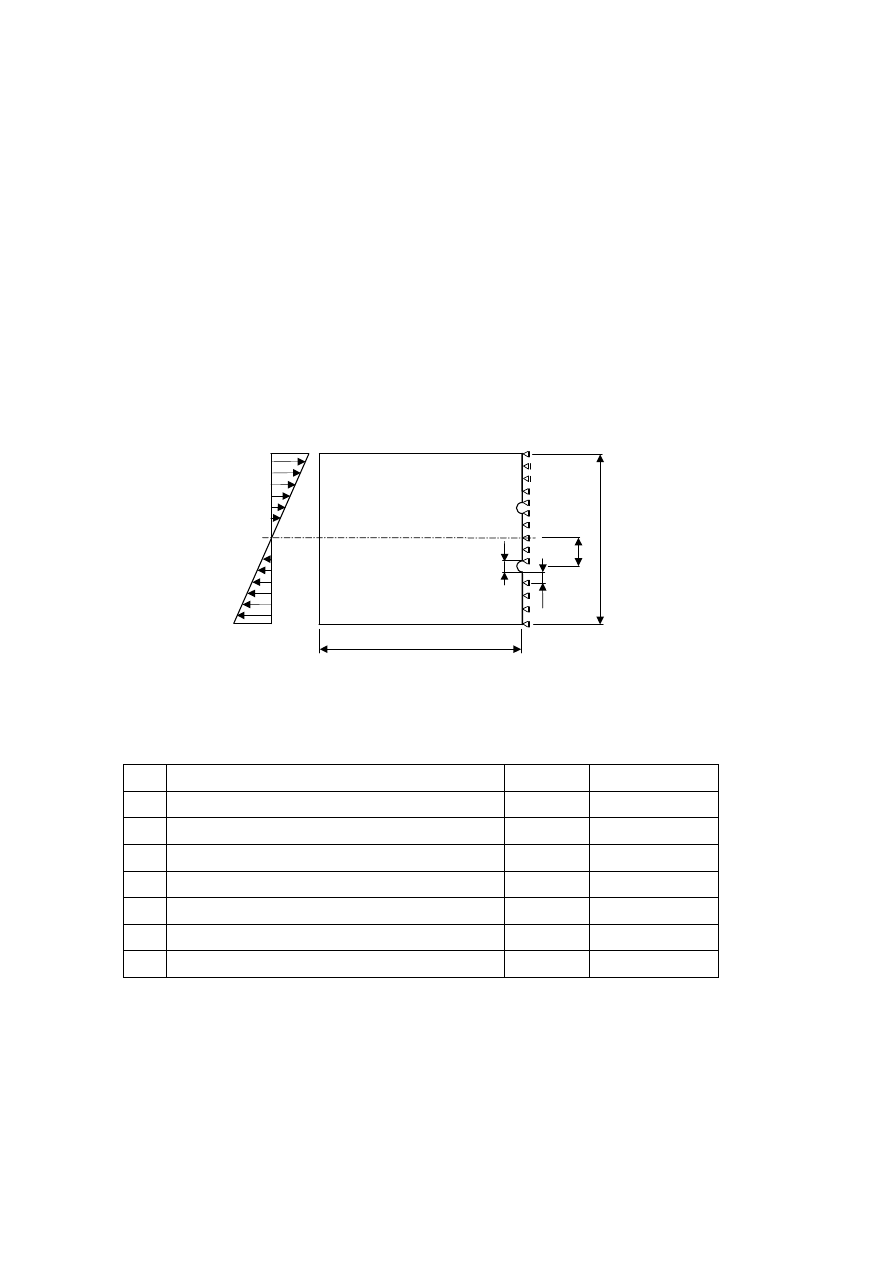
Rys. 4. Umiejscowienie pęknięcia o długości a w modelu obliczeniowym środnika dwuteownika stalowego
60
Analizując rozwój hipotetycznego pęknięcia, rozchodzącego się od zewnętrznego otworu
montażowego wykonanego w dwuteowniku stalowym, założono, że pęknięcie o krytycznej długości a
znajdować się będzie nadal w obszarze środnika (rys. 4). Znając rozkład naprężeń normalnych
w dwuteowniku stalowym, założono, że do analizy propagacji szczeliny w jego środniku wystarczy
przeanalizować rozkład naprężeń tylko w samym środniku.
Na rysunku 4 przedstawiono zarówno obszar kształtownika przyjęty do obliczeń, jak i wykres
naprężeń normalnych w tym obszarze konstrukcji. Ponieważ celem pracy było określenie wartości
współczynnika intensywności nie dla wybranego kształtownika, a dla wybranej grupy kształtowników,
należało zatem, przed przystąpieniem do obliczeń numerycznych, dokonać unifikacji wymiarów
dwuteowników zwykłych (normalnych). Zdecydowano się powiązać wszystkie wymiary potrzebne
do stworzenia modelu obliczeniowego z wysokością kształtowników, która jest ich wielkością
charakterystyczną.
W pierwszym etapie badań, aby określić schemat obliczeniowy dwuteownika, dokonano analizy
wymiarów geometrycznych dwuteowników zwykłych. Pod uwagę brano dwuteowniki o minimalnej
nominalnej wysokości 300 mm. W obliczeniach numerycznych MES omawianą konstrukcję
zamodelowano elementami powłokowymi. W modelu obliczeniowym ze względu na symetrię
konstrukcji i symetrię obciążenia rozpatrzono tylko połowę elementu z odpowiednimi warunkami
brzegowymi (rys. 5).
P
-P
X
D
a
b
p
/2
W
Rys. 5. Sposób podziału, podparcia i obciążenia analizowanego dwuteownika
W tablicy 1 przedstawiono wszystkie wielkości niezbędne do określenia modelu obliczeniowego
analizowanego środnika dwuteownika.
Tablica 1. Określenie wielkości występujących w przyjętym modelu obliczeniowym
Lp.
Wyszczególnienie
Symbol
Wzór
1. Wysokość dwuteownika
h
–
2. Wysokość środnika
W
W = h/1,12
3. Grubość środnika
B
B = h/28
4. Odległość otworu od osi obojętnej przekroju
X
X = h/10
5. Odległość między stężeniami poprzecznymi
b
p
b
p
= 3,85 h
6. Średnica otworów montażowych
D
D = h/20
7. Aktualna długość szczeliny
a
–
Obliczenia MES wykonano dla dwuteownika normalnego o wysokości 450 mm. Wybór tego
kształtownika podyktowany był faktem, że projekt koncepcyjnego wykorzystania tego typu
kształtowników oraz znormalizowanych stężeń poprzecznych jako przęsła został zaprojektowany
w roku 2001 w WSOWLąd. we Wrocławiu i przedstawiony w pracy [13].
Wykorzystując do obliczeń metodę elementów skończonych należy mieć na uwadze fakt,
że uzyskane rozwiązania obarczone są różnego rodzaju błędami. Aby upewnić się, co do poprawności
ich rozwiązań, należy przeanalizować zagadnienia dla różnych stopni zagęszczenia siatek elementów
skończonych, obserwując przy tym zbieżność rozwiązania. Zagęszczenie siatki elementów
skończonych prowadzi jednak do szeregu problemów związanych z rozwiązaniem zagadnienia
61
numerycznego (wielkość układu równań algebraicznych, czas obliczeń, wielkości błędów zaokrągleń,
błędów numerycznych itp.). W praktyce dąży się do stosowania takich podziałów, które pozwalałyby
na osiągnięcie dobrej dokładności obliczeń przy racjonalnych czasach ich uzyskiwania [11].
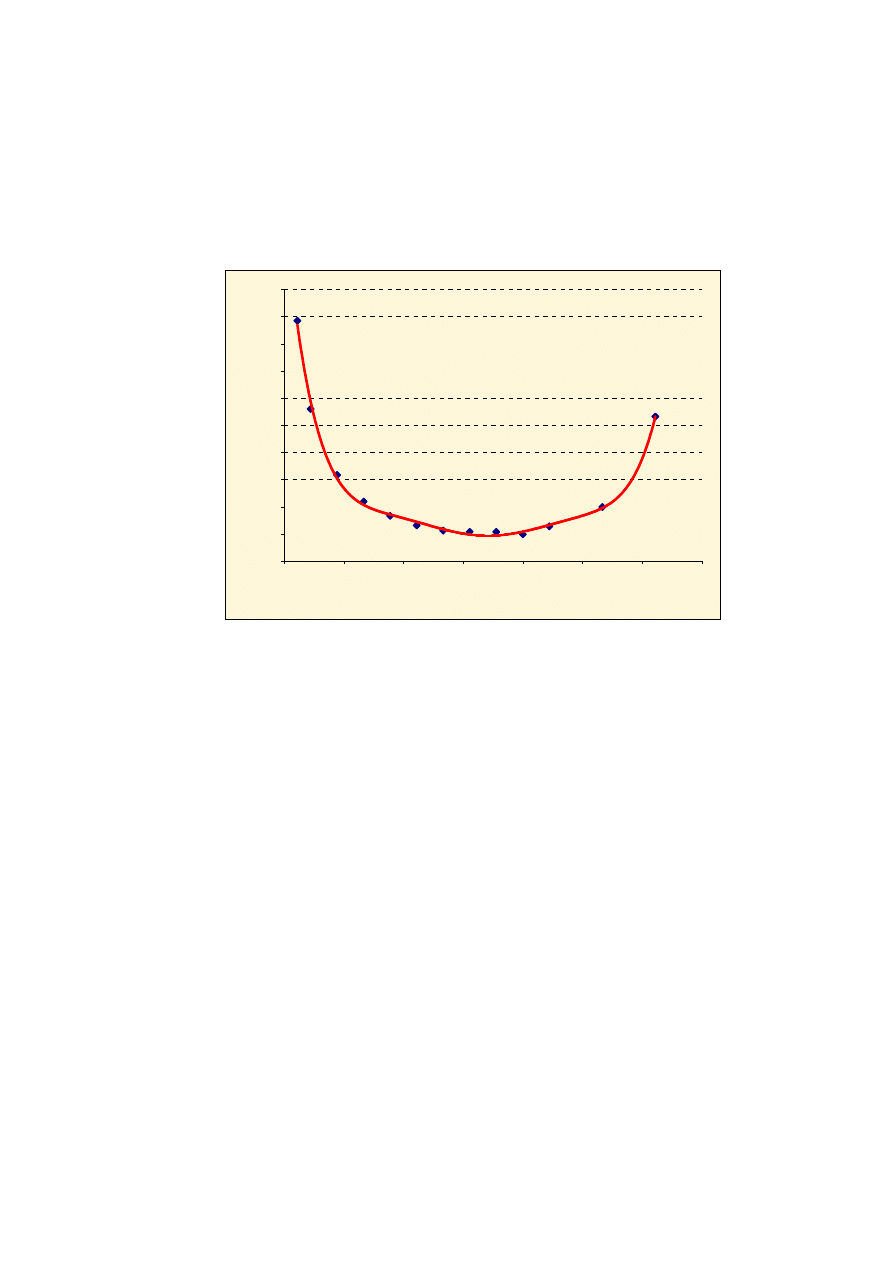
Zależność funkcyjna współczynnika kształtu Y od aktualnych wymiarów szczeliny a jest mało
praktyczna, gdyż umożliwia analizę propagacji pęknięcia jedynie dla dwuteownika o wysokości 450
mm. Aby zależność tę można było wykorzystywać dla całej grupy dwuteowników zwykłych niezbędne
jest uzależnienie wielkości współczynnika kształtu Y jednocześnie od aktualnych wymiarów szczeliny
(pęknięcia), jak i od wysokości kształtownika. Zależność spełniającą powyższe warunki przedstawiono
na wykresie (rys. 6).
y = 91578,56x
6
- 92665,21x
5
+ 37307,00x
4
- 7589,48x
3
+ 826,20x
2
- 47,13x + 1,90
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
Stosunek długości szczeliny a do wysokości dwuteownika H
W
sp
ó
łc
zy
n
n
ik
k
sz
ta
łt
u
Y
Rys. 6. Zależność wielkości współczynnika kształtu Y od stosunku długości szczeliny a
do wysokości dwuteownika h
Analizując dane przedstawione na rys. 6 zaproponowano, aby funkcyjny zapis wielkości
współczynnika kształtu Y przyjąć w postaci (13):
90
,
1
13
,
47
20
,
826
48
,
7589
00
,
37307
21
,
92665
56
,
91578
2
3
4
5
6
+
−
+
−
+
−
=
x
x
x
x
x
x
Y
(13)
gdzie x jest stosunkiem długości szczeliny a do wysokości dwuteownika h.
5. Podsumowanie
Biorąc pod uwagę czasochłonność prowadzonych obliczeń oraz minimalną liczbę niezbędnych
badań, wydaje się, że prowadzenie obliczeń zmęczeniowych w oparciu o podstawowy wzór
uwzględniający współczynnik asymetrii cyklu, tj. wzór Formana można uzyskać zadawalające wyniki.
Metoda wykorzystująca współczynnik intensywności naprężeń (oparta na kryterium siłowym)
wydaje się bardzo odpowiednia do praktycznego zastosowania. Wykorzystanie podstawowych
programów inżynierskich opartych na MES umożliwia określanie współczynnika intensywności
naprężeń dla dowolnego układu obiekt – szczelina – obciążenie.
W przypadku stalowych mostów niskowodnych stała materiałowa K
Ic
przestaje zazwyczaj
obowiązywać, stąd korzystanie z klasycznego siłowego kryterium pękania jest utrudnione. Należy
zatem pamiętać, że nieznaczne wymiary środników i pasów (grubość) mogą spowodować
występowanie złożonego stanu naprężeń przed wierzchołkiem szczeliny oraz zmianę długości strefy
plastycznej stosowanej w obliczeniach (2).
Reasumując, wykorzystanie kryterium siłowego do określenia pozostałej trwałości eksploatacyjnej
stalowych mostów wojskowych, mimo że obarczone są dość znacznym błędem, może być używane
jako jedno z istniejących, dopuszczalnych, rozwiązań. Obliczenia te jednak powinny być zawsze
dublowane przy wykorzystaniu innej ze znanych i stosowanych metod.
62
Wyprowadzone równanie na współczynnik kształtu Y ma bardzo utylitarny charakter. Znajomość
wartości tego współczynnika w postaci funkcyjnej umożliwia w prosty sposób szacowanie pozostałej
trwałości eksploatacyjnej stalowych mostów niskowodnych z tego rodzaju pęknięciem.
Należy zdawać sobie sprawę również z faktu, że przyjęte założenia o pracy dwuteownika i jego
pęknięciu mogą nie być wystarczające. Należy liczyć się m.in. z dwoma dodatkowymi czynnikami:
- w szczycie pęknięcia może powstać strefa plastyczna, co efektywnie przyczynia się do wydłużenia
pęknięcia i jednocześnie podnosi wartość K,
- obciążenie pęknięcia tylko według I mody otwarcia zaniża wytężenie materiału w szczelinie.
Ponadto należy zdać sobie sprawę z faktu, żeby wyprowadzona zależność funkcyjna była wiarygodna
powinna zostać zweryfikowana badaniami doświadczalnymi, co jest przewidziane w dalszym etapie
badań. Aktualnie jednak prowadzone są nadal analizy numeryczne nad omawianym rodzajem pęknięcia.
Literatura
[1] NEIMITZ A., Mechanika pękania. PWN, Warszawa 1998.
[2] DUCHACZEK A., KAMYK Z., MAŃKO Z., Określanie trwałości stalowych mostów
wojskowych z uwzględnianiem teorii mechaniki pękania. Systems Journal of Transdisciplinary
Systems Science, Vol. 7, Special Issue No. 1/2002, VI Międzynarodowa Konferencja Naukowa
Computer Aided Engineering, Polanica Zdrój, 5–8 czerwca 2002, s. 172–181.
[3] RYKALUK K., WICHTOWSKI B., Wytrzymałość konstrukcji mostowej z pęknięciami w spawanych
złączach czołowych. XLIII Konferencja Naukowa Komitetu Inżynierii Lądowej i Wodnej PAN i Ko-
mitetu Nauki PZITB, Poznań–Krynica, 15–21 września 1997, t. V, Konstrukcje Metalowe, s. 133–140.
[4] STURZBECHER K., Wytrzymałość eksploatacyjna starych mostów spawanych. XLIII
Konferencja Naukowa Komitetu Inżynierii Lądowej i Wodnej PAN i Komitetu Nauki PZITB,
Poznań–Krynica, 15–21 września 1997, t. V, Konstrukcje Metalowe, s. 113–118.
[5] SZATA M., Opis rozwoju zmęczeniowego pękania w ujęciu energetycznym. Oficyna Wydawnicza
Politechniki Wrocławskiej, Wrocław 2002.
[6] GERMAN J., Podstawy mechaniki pękania. Politechnika Krakowska, Kraków 2001.
(http://republika.pl/jger/pekanie – 1 luty 2003).
[7] KUBERA S., GÓRSKI Z., ROSOCHOWICZ K., JAKUBOWSKI M., Wpływ charakterystyki
materiału i czynników technologicznych na wytrzymałości zmęczeniową konstrukcji okrętowych.
Prace Instytutu Okrętowego Politechniki Gdańskiej, Gdańsk 1978.
[8] DUCHACZEK A., KAMYK Z., MAŃKO Z., Określenie trwałości elementów mostów stalowych
z wykorzystaniem teorii mechaniki pękania. Etapy I–III. Praca naukowo-badawcza WIW/457.
Wyższa Szkoła Oficerska im. T. Kościuszki, Wrocław 2001–2003.
[9] MARAKAMI Y., editor-in-chief, Stress intensity factors handbook. Vol. 1 i 2, Pergamon Press, 1987.
[10] TADA H., PARIS P. C., IRWIN G. R., The stress analysis of cracks. Del Research Corp.
Hallertown, Pa., 1973.
[11] JANECKI S., BIELECKI M., Żywotność łopatek wirnikowych osiowych maszyn przepływowych.
Temat 3, Zadanie 2, Część I, Ocena zmęczeniowego wzrostu pęknięć w łopatkach turbin parowych
w
środowisku
korozyjnym.
Projekt
Badawczy
nr
7T07B04816,
Gdańsk
1999.
(http://www.imp.gda.pl/fem/archiwum.htm – 15 czerwiec 2003).
[12] KOCAŃDA S., SZALA J., Podstawy obliczeń zmęczeniowych. PWN, Warszawa 1997.
[13] MAŃKO Z. i inni, Racjonalizacja wykorzystania materiałów miejscowych do budowy mostów
niskowodnych. Etapy I–III. Praca naukowo-badawcza WIW/439. Wyższa Szkoła Oficerska im. T.
Kościuszki, Wrocław 2001.
[14] BROEK D., Elementary engineering fracture mechanics. Kluwer Academic Publishers, Dordrecht 1986.
REMAINING LIFE ASSESSMENT OF STEEL GIRDERS
OF LOW-WATER BRIDGES
In the paper there is presented a manner of specifying the remaining life of steel girders of low-water bridges
in the case when the fatigue cracks have occurred. The given function that characterizes the geometry of the
element (the shape factor Y) for a chosen case of defect at the steel girders makes it possible to assess the
remaining life of low-water bridges easily. There are also given some limitations of using the strength criterion to
assess the remaining life of military bridges made of steel sections.
Document Outline