Politechnika Warszawska

Wydział Samochodów i Maszyn Roboczych

Instytut Maszyn Roboczych Ciężkich

Laboratorium Konstrukcji Nośnych

Ocena trwałości zmęczeniowej

Krzywa Woehlera

Wersja robocza

Tylko dla użytku wewnętrznego SiMR PW

Opracowanie:

Hieronim Jakubczak

Wojciech Sobczykiewicz

Warszawa 2006

Wszelkie prawa zastrzeżone

1. WSTĘP- CEL ĆWICZENIA

Zjawisko zmęczenia materiałów jest znane od ponad stu lat. Jednakże nadal nie został

rozstrzygnięty problem istoty zmęczenia. Istniejące hipotezy nie dają odpowiedzi na pytanie,
jakie są fizyczne przyczyny, źródła i mechanizmy rozwoju procesu zmęczenia. Notuje się
miast wiele prób formalnego opisu matematycznego tego zjawiska. Podstawą tego opisu są
ilościowe wyniki klasycznego aparatu poznawczego, jakim są metody eksperymentalne.
Stosowane są one nie tylko do badań podstawowych, lecz również jako weryfikacja założeń
konstrukcyjnych projektanta i to zarówno w wersji laboratoryjnej jak poligonowej.

Proces pękania zmęczeniowego jest bardzo złożony i można wydzielić w nim kilka faz.

Z punktu widzenia projektanta najważniejsze są dwie główne fazy: inicjacji oraz stabilnego
wzrostu pęknięcia. Współcześnie istnieją metody badań umożliwiające wyznaczenie
charakterystyk trwałości dla każdej z w/w faz rozwoju pęknięcia zmęczeniowego, jak również
metody prognozowania trwałości konstrukcji oparte o te charakterystyki.

W wielu przypadkach wykorzystuje się jednak charakterystykę zmęczeniową, która

obejmuje zwykle te dwie fazy rozwoju pęknięć zmęczeniowych. Jest to krzywa Woehlera,
będąca nadal podstawową charakterystyką zmęczeniową, wykorzystywaną w
projektowaniu elementów maszyn oraz konstrukcji nośnych narażonych na pękanie
zmęczeniowe.

Współczesne konstrukcje charakteryzują się, ze względów ekonomicznych,

ograniczonym okresem eksploatacji. Stawia to przed konstruktorem określone
wymagania z tytułu oceny trwałości zmęczeniowej. Tak więc już na etapie
projektowania musi on posiadać możliwie pełną informację o własnościach
zmęczeniowych materiału, czy też wręcz tzw. potencjalnego słabego ogniwa (PSO), tj.
krytycznego miejsca, decydującego o trwałości konstrukcji.

Zasadniczym celem ćwiczenia jest określenie parametrów charakterystyki

zmęczeniowej stosowanej w procesie wymiarowania konstrukcji nośnej, oraz
oszacowanie na tej podstawie trwałości dla wymaganych warunków eksploatacji. W
ć

wiczeniu przedstawione zostały podstawowe metody wyznaczania charakterystyk

trwałości oraz statystycznego opracowania wyników eksperymentu.

2. WPROWADZENIE TEORETYCZNE

2.1. Podstawowe wiadomości o charakterystykach trwałości zmęczeniowej

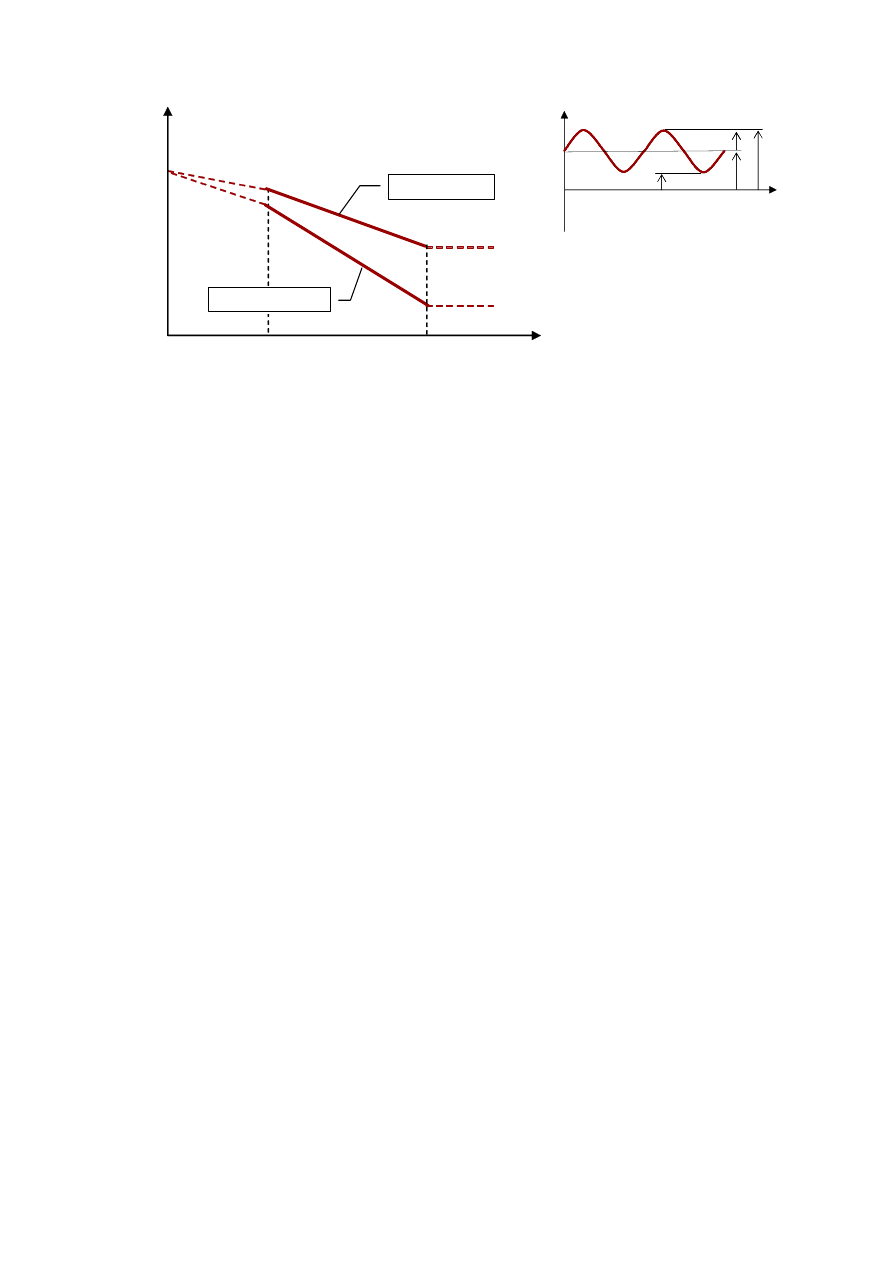
Pojęcie wytrzymałości zmęczeniowej i krzywej Woehlera, jako podstawowe, w

wytrzymałości materiałów, są powszechnie znane. Istnieje na ten temat znaczna
liczba publikacji np. [l], [2], [3]. Jednakże dla porządku zostaną one zdefiniowane.

Wytrzymałość zmęczeniowa rozumiana jest jako naprężenie

σ

D

(dla określonego

cyklu naprężeń), przy którym element badany nie ulegnie zniszczeniu po osiągnięciu
umownej, bazowej liczby cykli N

o

(rys. 1). Krzywa Woehlera (KW) jest niejako zbiorem

wytrzymałości zmęczeniowych dla różnych liczb cykli i powstaje w efekcie
doświadczenia przeprowadzonego w ściśle określonych warunkach.

Naprężenie

σ

D

jest naprężeniem nominalnym (globalnym), wyznaczonym zwykle

w punkcie, w którym następuje inicjacja pęknięcia zmęczeniowego i może być
definiowane jako: amplituda –

σ

a

, zakres –

∆

σ

. = 2

σ

a

, bądź też jako naprężenie

maksymalne cyklu obciążeń –

σ

max

.

N

1

N

0

log N

log

σ

R

m

σ

1

1

σ

D

σ

DK

Próbka gładka

Próbka z karbem

Rys. 1 Parametry opisujące krzywą Woehlera

Krzywa Woehlera jest przedstawiana jako prosta w układzie współrzędnych

log

σ

– log N w zakresie liczby cykli N

1

– N

o

i jest opisywana równaniem:

const

N

N

o

m

D

m

=

=

σ

σ

(1)

gdzie

m

jest wykładnikiem KW, a jego odwrotność opisuje kąt nachylenia krzywej.

Jako bazową liczbę cykli przyjmuje się dla stali zwykle

N

o

= 2E+6 cykli,

jednakże często ta granica jest obecnie przesuwana do 5 lub 10 mln. cykli.

N

1

to

liczba cykli, która wyznacza początek krzywej Wohlera, wynosi ona około

N

1

=

10E+3 do 10E+4 cykli.

Wytrzymałość zmęczeniowa elementu z karbem,

σ

DK

jest mniejsza od

wytrzymałości elementu gładkiego,

σ

D

, a ich związek opisuje współczynnik działania

karbu

β

K

, obliczany jako stosunek

σ

D

do

σ

DK

. Warto podkreślić, że wartość

β

K

odnosi

się do

N

=

N

o

, natomiast dla

N

<

N

o

obserwuje się zwykle mniejsze wartości stosunku

naprężeń

σ

/

σ

K

. Dla uproszczenia przyjmuje się często dwie skrajne koncepcje:

1. KW zbiegające się w punkcie

σ

1

,

N

1

,

2. KW równolegle, tj. o stałym stosunku

σ

/

σ

DK

=

σ

/

σ

DK

=

β

K

. (taka koncepcja

została przyjęta w normach dotyczących KW dla konstrukcji spawanych).

Współczynnik działania karbu jest związany ze współczynnikiem koncentracji

naprężeń,

α

K

zależnym od geometrii karbu poprzez tzw. współczynnik wrażliwości

materiału na działanie karbu,

q

:

)

(

q

K

K

1

1

−

+

=

α

β

(2)

którego warto

ść

zale

ż

y zarówno od wytrzymało

ś

ci materiału, R

m

, jak równie

ż

od

promienia karbu,

ρ

(im mniejszy promie

ń

, tym mniejsza warto

ść

q).

Nale

ż

y pami

ę

ta

ć

,

ż

e wytrzymało

ść

zm

ę

czeniowa zale

ż

y równie

ż

od takich

czynników, jak:

•

stan warstwy powierzchniowej, opisywany współczynnikiem

β

p

,

•

współczynnik asymetrii cyklu, r =

σ

min

/

σ

max

•

wielko

ść

elementu, opisywana współczynnikiem

γ

, i inne.

σ

min

σ

max

σ

m

σ

a

σ

0

czas

Krzywa Woehlera charakteryzuje zdolno

ść

elementu badanego do przenoszenia

napr

ęż

e

ń

zmiennych jednak

ż

e tylko dla konkretnego sposobu (cyklu) obci

ąż

enia.

Zwi

ą

zek

pomi

ę

dzy

warto

ś

ci

ą

wytrzymało

ś

ci

a

rodzajem

obci

ąż

enia,

reprezentowanym przez współczynnik asymetrii cyklu r wyznaczaj

ą

tzw. wykresy

zbiorcze. Nale

żą

do nich znane krzywe np. Smitha, Haigha.

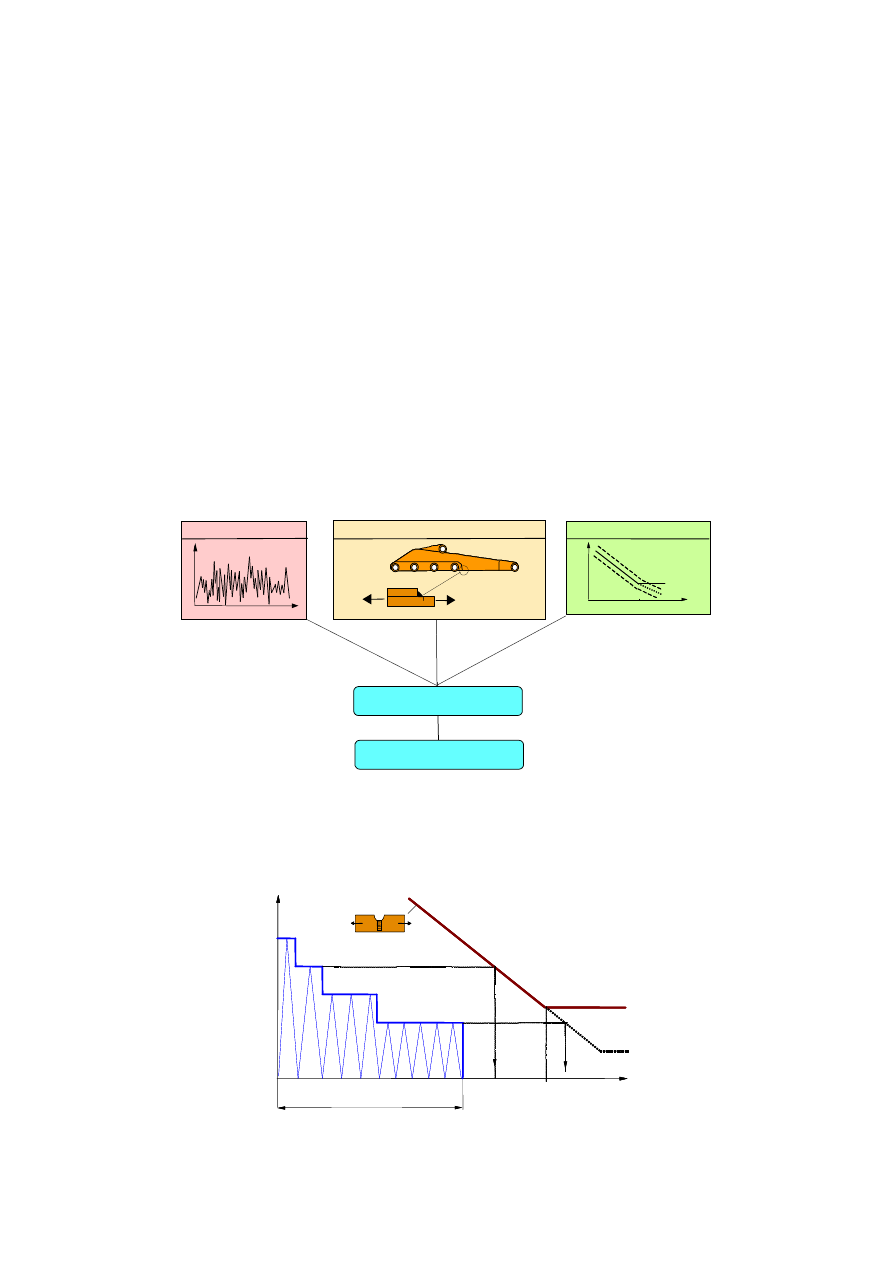
2.2 Prognozowanie trwałości zmęczeniowej

Prognozowanie trwało

ś

ci zm

ę

czeniowej elementów konstrukcyjnych jest procesem do

ść

zło

ż

onym i wymaga starannego okre

ś

lenia wszystkich danych, niezb

ę

dnych dla osi

ą

gni

ę

cia

poprawnego wyniku. Składa si

ę

ono z nast

ę

puj

ą

cych kroków (rys. 2):

1.

wyznaczenie potencjalnych miejsc (PSO), w których mog

ą

si

ę

zainicjowa

ć

p

ę

kni

ę

cia

zm

ę

czeniowe (s

ą

to zwykle karby).

2.

dobór KW, najbardziej odpowiedniej do analizowanego PSO (sposób obci

ąż

enia i

p

ę

kania),

3.

okre

ś

lenie obci

ąż

e

ń

eksploatacyjnych, okre

ś

lonych zwykle na podstawie pomiarów

tensometrycznych,

4.

obliczenie trwało

ś

ci zm

ę

czeniowej przy wykorzystaniu wybranej hipotezy kumulacji

uszkodze

ń

zm

ę

czeniowych.

ELEMENT KONSTRUKCJI

PSO

ELEMENT KONSTRUKCJI

PSO

MATERIAŁ

N

o

N

∆σ

σ

D

MATERIAŁ

N

o

N

∆σ

σ

D

OBCIĄŻENIE

σ

t

OBCIĄŻENIE

σ

t

TRWAŁOŚĆ

ANALIZA TRWAŁOŚCI

Rys. 2 Schemat oceny trwało

ś

ci zm

ę

czeniowej.

Obliczanie trwało

ś

ci zm

ę

czeniowej dla obci

ąż

e

ń

eksploatacyjnych, opisanych widmem

obci

ąż

e

ń

jest przedstawiona na rys. 3.

n

p

n

1

∆σ

2

cykle

N

0

N

2

σ

D

∆σ

max

Z

a

k

re

s

n

a

p

rę

ż

e

ń

σ

n

2

n

3

n

4

σ

’

D

n

p

n

1

∆σ

2

cykle

N

0

N

2

σ

D

∆σ

max

Z

a

k

re

s

n

a

p

rę

ż

e

ń

σ

n

2

n

3

n

4

σ

’

D

Rys. 3 Schemat obliczania uszkodze

ń

zm

ę

czeniowych

Przy oznaczeniach przedstawionych na rys. 3 trwało

ść

zm

ę

czeniowa, obliczona z

zastosowaniem liniowej hipotezy kumulacji uszkodze

ń

zm

ę

czeniowych (Palmgrena-Minera –

[4]), wyra

ż

ona poprzez liczb

ę

powtórze

ń

zarejestrowanego bloku obci

ąż

e

ń

eksploatacyjnych

jest wyra

ż

ona nast

ę

puj

ą

cym wzorem:

∑













=

k

i

m

i

o

m

max

DK

n

)

s

(

N

d

BLK

σ

∆

σ

∆

(3)

gdzie n

i

jest liczb

ą

cykli za

ś

s

i

=

∆σ

i

/

∆σ

max

– napr

ęż

eniem wzgl

ę

dnym dla i-tego stopnia

widma napr

ęż

e

ń

, za

ś

d jest krytyczn

ą

warto

ś

ci

ą

uszkodzenia zm

ę

czeniowego (zwykle

przyjmuje si

ę

d = 1).

Liczb

ę

cykli zmian napr

ęż

e

ń

N otrzymuje si

ę

przez pomno

ż

enie liczby powtórze

ń

bloku

obci

ąż

enia, BLK przez liczb

ę

cykli w bloku, n

p

.

Według klasycznej hipotezy P-M napr

ęż

enia poni

ż

ej wytrzymało

ś

ci zm

ę

czeniowej

σ

D

nie powoduj

ą

ż

adnych uszkodze

ń

zm

ę

czeniowych, jednak

ż

e zasada ta dotyczy tylko obci

ąż

e

ń

o stałej amplitudzie. W przypadku obci

ąż

e

ń

o zmiennej amplitudzie, wyst

ę

puj

ą

cych zwykle w

eksploatacji, krzyw

ą

Woehlera przedłu

ż

a si

ę

poprzez obni

ż

enie wytrzymało

ś

ci zm

ę

czeniowej

σ

D

do warto

ś

ci

σ

'

D

= (0.3 – 0.5)

σ

D

.

2.3 Krzywa trwałości

Wymiarowanie trwało

ś

ciowe konstrukcji oparte na prognozowaniu trwało

ś

ci w

powy

ż

szy sposób jest bardzo proste, jednak

ż

e ma kilka wad, z których najwa

ż

niejsze

to:
1.

trudno

ść

w odniesieniu p

ę

kni

ę

cia próbki do elementu konstrukcyjnego przy

znacznej ró

ż

nicy wymiarów

2.

brak mo

ż

liwo

ś

ci uwzgl

ę

dniania wpływu historii obci

ąż

e

ń

na trwało

ść

przy

stosowaniu hipotezy P-M.

Druga z tych niedoskonało

ś

ci mo

ż

e by

ć

wyeliminowana w znacznym stopniu

poprzez zast

ą

pienie KW przez krzyw

ą

trwało

ś

ci. W tym przypadku próbki, słu

żą

ce

zbudowaniu krzywej obci

ąż

one s

ą

widmem napr

ęż

e

ń

, reprezentuj

ą

cym powtarzalny blok

obci

ąż

e

ń

eksploatacyjnych).

Wytrzymało

ść

eksploatacyjn

ą

definiuje si

ę

jako maksymalne napr

ęż

enie w widmie,

ale z uwzgl

ę

dnieniem pozostałych napr

ęż

e

ń

wraz z ich cz

ę

sto

ś

ci

ą

wyst

ę

powania (czyli

form

ą

widma), przy której element badany nie ulegnie zniszczeniu po przekroczeniu

umownej, bazowej liczby cykli N

o

.

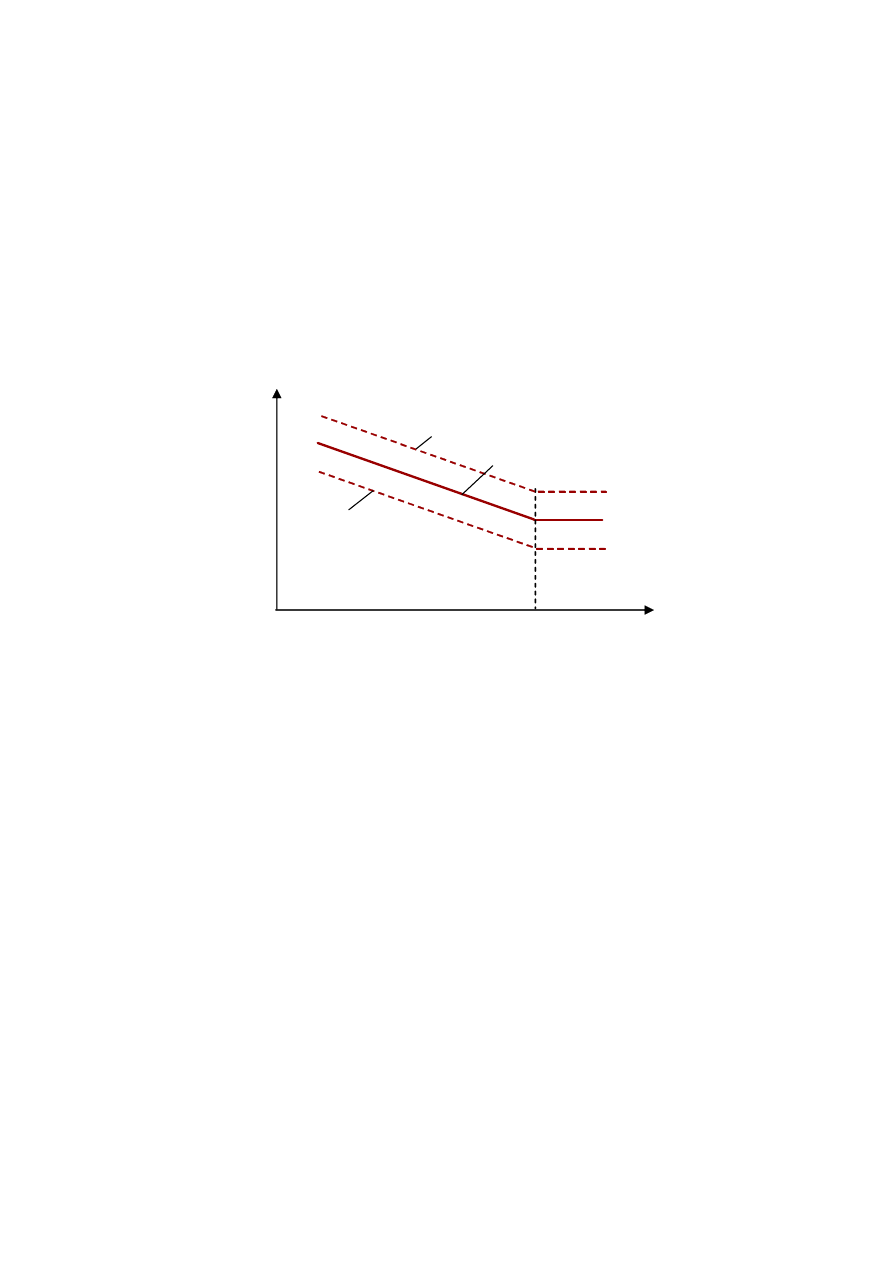
Na rys. 4 przedstawione zostały do

ś

wiadczalnie otrzymane krzywe trwało

ś

ci dla

ró

ż

nych widm eksploatacyjnych. S

ą

one równoległe do KW i znacznie przesuni

ę

te w

kierunku wi

ę

kszych trwało

ś

ci. Im mniej wypełnione jest widmo, mniej intensywne

obci

ąż

e

ń

tym wi

ę

ksze przesuni

ę

cie wykresu. Dla krzywych trwało

ś

ci stosuje si

ę

podobnego typu idealizacj

ę

wykresu w układzie podwójnie logarytmicznym jak dla

krzywej Woehlera. Równie

ż

zale

ż

no

ść

napr

ęż

e

ń

od liczby cykli ma ten sam charakter jak

w KW.

Krzywa trwało

ś

ci odzwierciedla wi

ę

c jak gdyby do

ś

wiadczalnie uzyskan

ą

liczb

ę

powtórze

ń

bloku obci

ąż

e

ń

, reprezentatywnego dla okre

ś

lonych warunków eksploatacji.

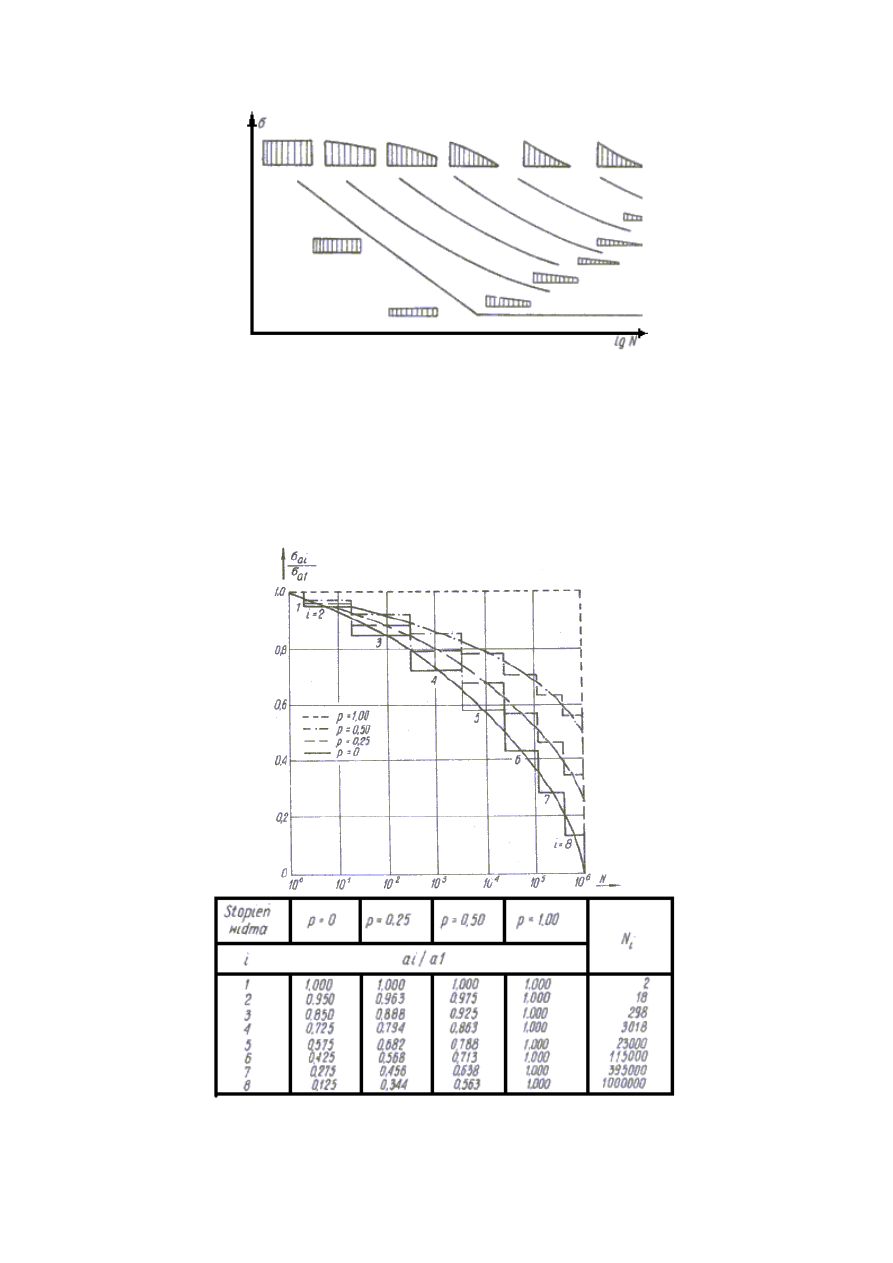
Rys. 4. Zmiana wytrzymało

ś

ci eksploatacyjnej w zale

ż

no

ś

ci od formy widma.

Aby widmo napr

ęż

e

ń

mo

ż

na było wykorzysta

ć

w próbie wytrzymało

ś

ci

eksploatacyjnej, tj. do wyznaczenia krzywej trwało

ś

ci, nale

ż

y je zamieni

ć

na

kilkustopniowy blok (program) obci

ąż

e

ń

(rys. 5). Powszechnie stosowany, wr

ę

cz

klasyczny, stał si

ę

sposób konstruowania programu obci

ąż

e

ń

zaproponowany przez E.

Gassnera. Na rys. 5 przedstawiono sposób budowy tzw. gassnerowskiego bloku
obci

ąż

enia dla ró

ż

nych współczynników widma.

Rys.5. Dyskretyzacja widma w zale

ż

no

ś

ci od stopnia wypełnienia (wg Gassnera).

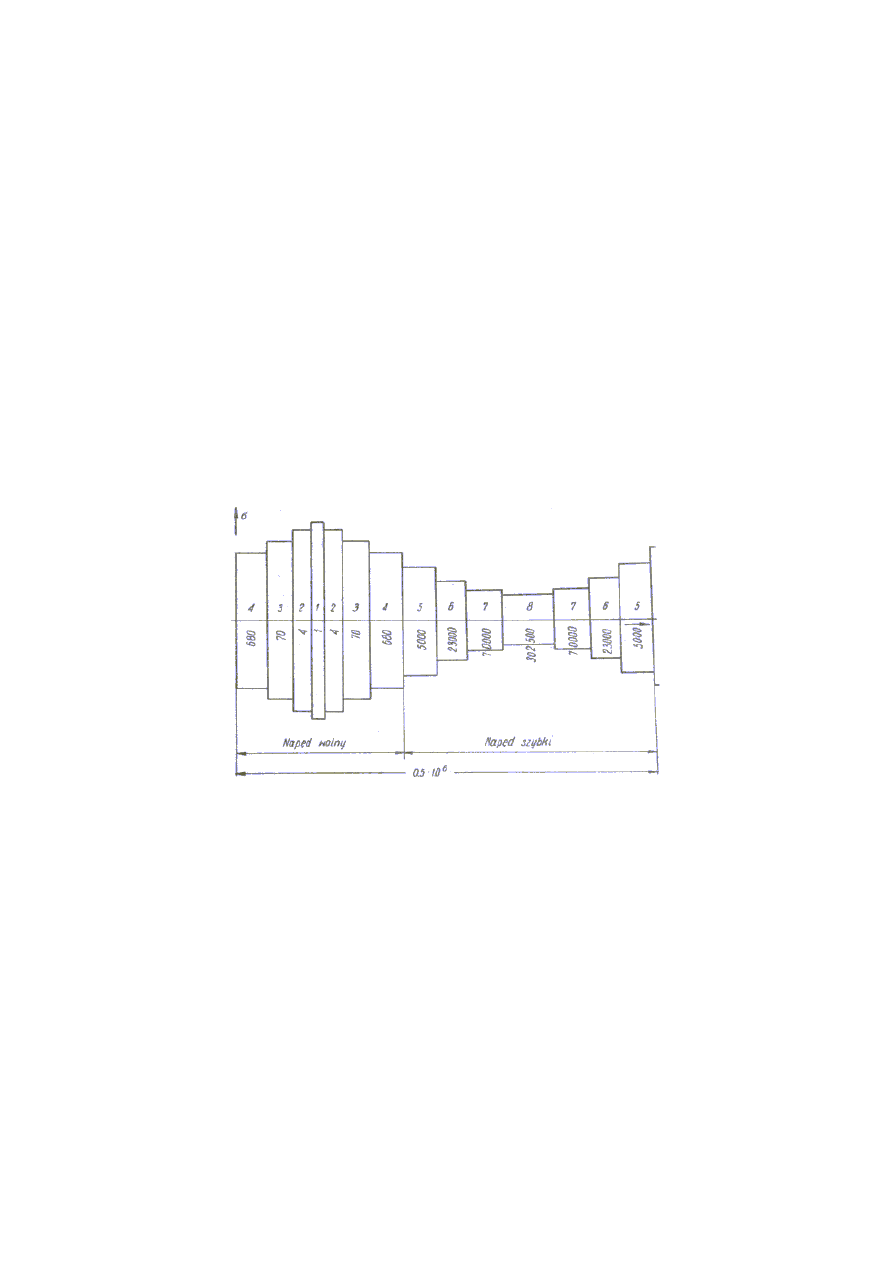
Symbole z indeksem "i" oznaczaj

ą

parametry dowolnego i-tego stopnia widma

za

ś

indeks "l" dotyczy pierwszego stopnia o najwi

ę

kszym obci

ąż

eniu.

Próby wytrzymało

ś

ci eksploatacyjnej mog

ą

by

ć

prowadzone dla ró

ż

nych warunków

obci

ąż

enia (np. w bloku gassnerowskim):

•

napr

ęż

enie

ś

rednie jest stałe we wszystkich stopniach widma.

σ

mi

=

σ

m1

=

const,

•

współczynnik, asymetrii cyklu jest stały we wszystkich stopniach widma r

i

= r

1

=

const,

•

napr

ęż

enie

ś

rednie i współczynnik asymetrii cyklu s

ą

ró

ż

ne dla ka

ż

dego stopnia

widma

σ

mi

≠

const, r

i

≠

const,

•

stała warto

ść

napr

ęż

enia minimalnego b

ą

d

ź

maksymalnego w ka

ż

dym stopniu

widma

σ

min

=

σ

min1

,

σ

max

=

σ

max1

Wybór jednej z powy

ż

szych opcji zale

ż

głównie od rzeczywistego przebiegu obci

ąż

e

ń

eksploatacyjnych, którego uproszczony opis stanowi widmo obci

ąż

e

ń

.

W celu uwzgl

ę

dnienia wpływu historii obci

ąż

e

ń

na trwało

ść

(tu na krzyw

ą

trwało

ś

ci)

program obci

ąż

e

ń

nie jest dokładnym powtarzaniem widma, lecz mo

ż

e wygl

ą

da

ć

tak, jak

przedstawiona rys. 6. Niekiedy stosuje si

ę

równie

ż

losowe rozmieszczanie kolejnych stopni

widma.

Rys. 6 Program obci

ąż

e

ń

w próbie wytrzymało

ś

ci eksploatacyjnej (wg Gassnera)

2.4. Technika eksperymentalnego otrzymywania krzywych Woehlera i

trwałości.

Przy zadanym sposobie wprowadzania obci

ąż

e

ń

metodyka przeprowadzania

eksperymentu w celu otrzymania KW i KT jest identyczna. Kształt oraz wielko

ść

próbek wymaganych do bada

ń

zm

ę

czeniowych okre

ś

lone s

ą

normami podobnie jak

wymagania dotycz

ą

ce sposobu prowadzenia prób.

Badania zm

ę

czeniowe próbek rozpoczyna si

ę

od obci

ąż

enia wywołuj

ą

cego

najwi

ę

ksz

ą

warto

ść

napr

ęż

enia maksymalnego (

σ

max

< R

e

) notuj

ą

c ilo

ść

cykli, które

doprowadziły do zniszczenia próbki (na ogół jako zniszczenie traktuje si

ę

całkowite

p

ę

kni

ę

cie

próbki).

Nast

ę

pne

próbki

podlegaj

ą

obci

ąż

eniu

odpowiednio

zmniejszonemu. Prób

ę

prowadzi si

ę

tak długo, a

ż

dla kolejnej próbki rejestruje si

ę

ilo

ść

cykli wi

ę

ksz

ą

b

ą

d

ź

równ

ą

bazowej N

o

. Wszystkie badania prowadzi si

ę

przy

zachowaniu stałej warto

ś

ci współczynnika asymetrii cyklu r = const.

Dopuszcza si

ę

, aby ka

ż

dy poziom pomiarowy reprezentowany był tylko przez

jeden wynik, jednak powtarzanie bada

ń

na ka

ż

dym poziomie pomiarowym napr

ęż

enia

(2

÷

3 wyników) znacznie poprawia dokładno

ść

parametrów wyznaczanych KW. Zwykle

badania próbek wykazuj

ą

cych znaczny rozrzut wyników (np. zł

ą

cza spawane) prowadzi

si

ę

przy wi

ę

kszej liczbie powtórze

ń

dla tego samego poziomu napr

ęż

e

ń

(nawet do 5), a

dla krzywych trwało

ś

ci przyjmuje si

ę

liczba ta jest jeszcze wi

ę

ksza. Minimalna ilo

ść

próbek dla tej procedury badawczej wynosi 8

÷

12.

Opracowanie wyników bada

ń

polega na wyznaczeniu głównych parametrów,

opisuj

ą

cych KW:

σ

D

i m w analizie statystycznej. Dokonuje si

ę

równie

ż

oszacowania

rozrzutu wyników przedziałami ufno

ś

ci dla prawdopodobie

ń

stw przetrwania P

U

= 90;

50; 10% (rys. 7). Niekiedy zakłada si

ę

z góry okre

ś

lon

ą

, stał

ą

warto

ść

wykładnika

krzywej m, np. dla zł

ą

czy spawanych przyjmuje si

ę

,

ż

e wynosi ona 3 lub 3.5.

N

0

log N

log

σ

σ

D,50%

σ

D,10%

σ

D,90%

P

u

= 10%

P

u

= 10%

P

u

= 50%

Rys.7. Krzywe Woehlera otrzymane wg procedury Woehlera.

Dla krzywych Woehlera przyjmuje si

ę

bazow

ą

liczb

ę

cykli N

o

= 2*10

6

, natomiast

dla krzywych trwało

ś

ci baza uzale

ż

niona jest bezpo

ś

rednio od formy widma i musi by

ć

ka

ż

dorazowo ustalona w do

ś

wiadczeniu. Podobnie wygl

ą

da sytuacja z lewostronn

ą

granic

ą

liczby. To ograniczenie wynika

ć

mo

ż

e z warto

ś

ci granicy plastyczno

ś

ci materiału i nie jest to

bynajmniej przypadek hipotetyczny. Zdarza si

ę

bowiem,

ż

e obliczona wytrzymało

ść

eksploatacyjna jest równa b

ą

d

ź

wi

ę

ksza granicy plastyczno

ś

ci. Oznacza to,

ż

e o trwało

ś

ci

konstrukcji decyduj

ą

„obci

ąż

enia dora

ź

ne" a nie "zm

ę

czeniowe".

2.4. Opracowanie statystyczne wyników eksperymentu

Jak ju

ż

wspomniano wyznaczenie zale

ż

no

ś

ci log

σ

- log N dokonuje si

ę

poprzez

statystyczne opracowanie wyników bada

ń

, oparte o analiz

ę

regresji i metod

ę

najmniejszych kwadratów.

Wyniki bada

ń

zm

ę

czeniowych mo

ż

na przedstawi

ć

w postaci wektora W

i

= [N

i

,

σ

i

]

(i = l,..,n), gdzie współrz

ę

dna N

i

ma charakter losowy. W zwi

ą

zku z tym,

ż

e KW jest

opisana równaniem (1) i w układzie podwójnie logarytmicznym tworzy lini

ę

prost

ą

(ln C = ln

σ

+ 1/m ln N), wektor W

i

lepiej jest zast

ą

pi

ć

wektorem W’

i

= [X

i

, Y

i

], którego

składowe s

ą

okre

ś

lone jako: Y

i

= ln

σ

i

, X

i

= ln N

i

.

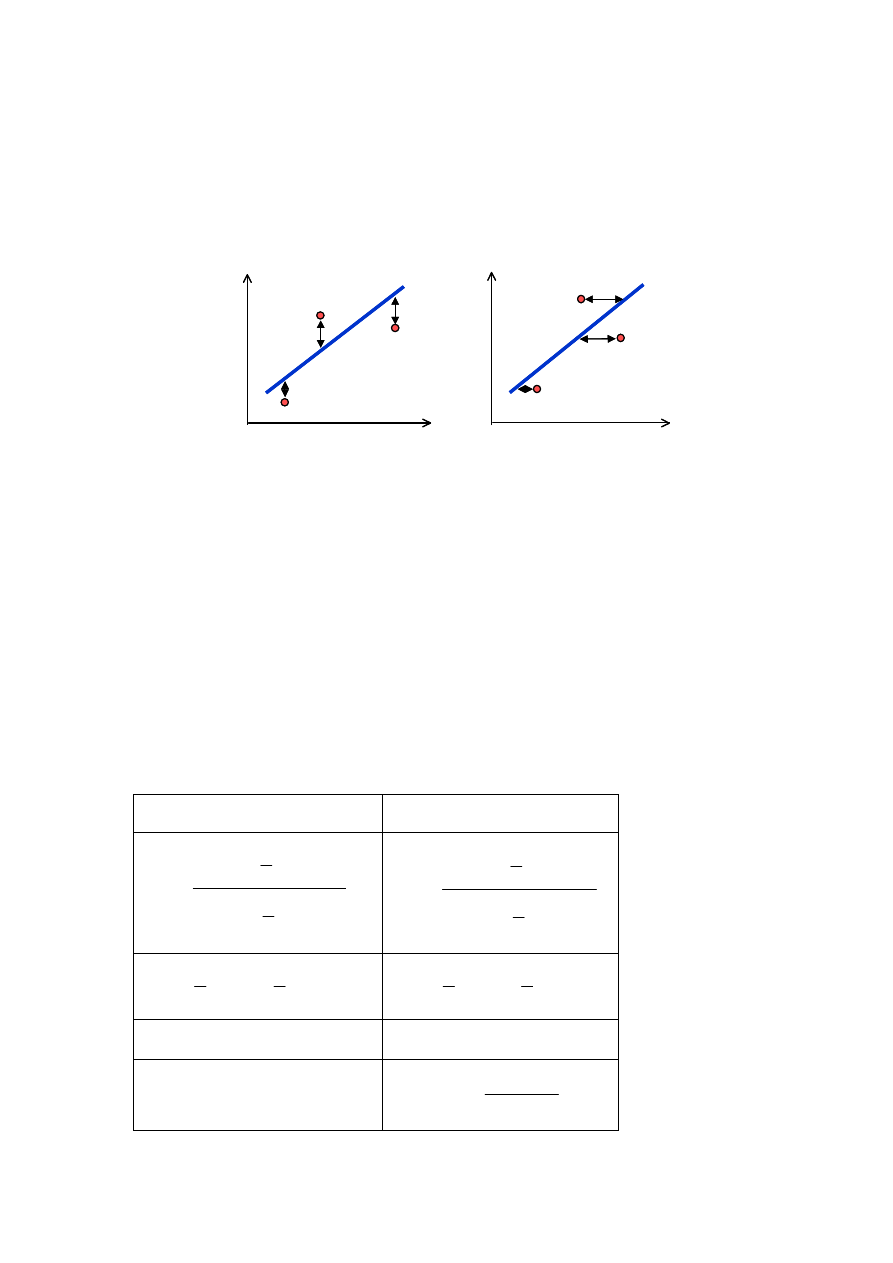
Poszukiwana jest liniowa funkcja postaci Y = a + bX, która w zakresie

ograniczonej wytrzymało

ś

ci zm

ę

czeniowej w sposób "najlepszy" wi

ąż

e ze sob

ą

współrz

ę

dne wektora W

i

. Zadanie sprowadza si

ę

do znalezienia takich warto

ś

ci

współczynników a i b, dla których warto

ś

ci bezwzgl

ę

dne sumy kwadratów „bł

ę

dów” s

ą

najmniejsze. Bł

ę

dy s

ą

okre

ś

lane jako ró

ż

nice odległo

ś

ci punktów eksperymentu od linii

ś

redniej i mog

ą

by

ć

‘mierzone’ wzdłu

ż

osi pionowej (RRY) lub poziomej (RRX) -

rys. 8,

x

y

x

y

x

y

x

y

Rys. 8. Regresja liniowa wzgl

ę

dem osi Y (RRY) i X (RRX)

za

ś

odpowiednie równania minimalizowanej sumy bł

ę

dów s

ą

nast

ę

puj

ą

ce:

∑

−

+

=

N

i

i

i

)

b

,

a

min(

)

Y

bX

a

(

F

2

(RRY)

(4)

∑

−

+

=

N

i

i

i

)

b

,

a

min(

)

X

bY

a

(

F

2

(RRX)

(5)

Wzory do obliczania parametrów KW za pomoc

ą

regresji liniowej s

ą

zestawione w

Tabeli 1. W tabeli zawarte s

ą

równie

ż

wzory do obliczania

ś

redniej warto

ś

ci granicy

zm

ę

czenia dla przyj

ę

tej warto

ś

ci bazowej liczby cykli N

o

, np. N

o

= 2E+6.

Tabela 1. Wzory do obliczenia parametrów KW

RRY

RRX

2

2

1

1













−

−

=

∑

∑

∑

∑

∑

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

i

x

n

x

y

x

n

y

x

b

2

2

1

1













−

−

=

∑

∑

∑

∑

∑

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

i

y

n

y

y

x

n

y

x

b

∑

∑

−

=

n

i

i

n

i

i

x

n

b

y

n

a

1

1

∑

∑

−

=

n

i

i

n

i

i

y

n

b

x

n

a

1

1

b

/

m

1

−

=

b

m

−

=

( )

[

]

o

D

N

ln

b

a

exp

+

=

σ

( )













−

=

b

a

N

ln

exp

o

D

σ

Rozrzut danych wzgl

ę

dem linii

ś

redniej KW mo

ż

na oszacowa

ć

poprzez współczynnik

korelacji

ρ

, obliczany z zale

ż

no

ś

ci (warto

ść

współczynnika korelacji le

ż

y zawsze w

przedziale



ρ

XY



< l):

∑

∑

∑

−

−

−

−

=

N

i

sr

i

N

i

sr

i

N

i

sr

i

sr

i

XY

)

Y

Y

(

)

X

X

(

)

Y

Y

)(

X

X

(

2

2

ρ

(6)

gdzie

∑

=

=

n

i

i

ś

r

X

n

X

1

1

,

∑

=

=

n

i

i

ś

r

Y

n

Y

1

1

(7)

lub poprzez odchylenie standardowe warto

ś

ci Y:

∑

−

=

N

i

mi

i

Y

)

Y

Y

(

n

1

s

2

(8)

gdzie Y

mi

s

ą

warto

ś

ciami

ś

rednimi (le

żą

cymi na

ś

redniej KW), obliczonymi według

zale

ż

no

ś

ci:

i

mi

bX

a

Y

+

=

(9)

Na ogół rozrzut punktów do

ś

wiadczalnych Y

i

wokół

ś

redniej KW podlega rozkładowi

normalnemu, co oznacza,

ż

e rozrzut wytrzymało

ś

ci zm

ę

czeniowej

σ

D

podlega rozkładowi

log-normalnemu.

W przypadku, gdy ilo

ść

wyników jest du

ż

a (n > 6), nale

ż

y dokona

ć

sprawdzenia czy

skrajne z nich nie s

ą

obarczone du

ż

ymi bł

ę

dami oraz czy podlegaj

ą

one prawu rozkładu

normalnego.

Nale

ż

y zauwa

ż

y

ć

,

ż

e dla oszacowanej warto

ś

ci

ś

redniej wytrzymało

ś

ci zm

ę

czeniowej,

wyznaczonej na podstawie ograniczonej liczby próbek, wyznacza si

ę

warto

ść

ś

redni

ą

populacji (populacja oznacza wszystkie mo

ż

liwe próbki). Dokonuje si

ę

tego poprzez

okre

ś

lenie przedziałów ufno

ś

ci na poziomie istotno

ś

ci 10%, którego warto

ść

jest

standardowa, w opracowaniu wyników bada

ń

zm

ę

czeniowych.

3. Wykonanie ćwiczenia

1.

Zadaniem ka

ż

dego ze studentów w oparciu o otrzymane wyniki próby zm

ę

czeniowej jest:

•

przedstawi

ć

wyniki próby zm

ę

czeniowej graficznie,

•

obliczy

ć

parametry

ś

rednie KW (m,

σ

D

) oraz odchylenie standardowe s

Y

,

•

otrzymane wyniki nanie

ść

na wykres, wyznaczaj

ą

c przedział +/- 3 s

Y

,

2.

Wykorzystuj

ą

c wyznaczon

ą

KW obliczy

ć

trwało

ść

zm

ę

czeniow

ą

dla zadanego widma

obci

ąż

e

ń

eksploatacyjnych.

3.

Napisa

ć

wnioski.

4. Literatura

[l] Koca

ń

da, S.: Zm

ę

czeniowe niszczenie metali. WNT 1972.

[2] Katarzy

ń

ski, S., Koca

ń

da, S., Zakrzewski, M.: Badanie własno

ś

ci mechanicznych metali,

WNT 1967.

[3] Dietrych, M., Koca

ń

da, S., Korewa, W.: Podstawy konstrukcji maszyn, WNT 1964.

[4] Nowak, B., Saal, H., Seeger, T.: Ein Vorschlag zur Schwingfestigkeitsbemessung

von Bauteilen aus hochfesten Baustahlen.