Wyższa Szkoła Przedsiębiorczości

i Zarządzania im. L. Koźmińskiego

Warszawa,

2005

Jan M. Myszewski

Techniki wspomagające zarządzanie jakością

Metody

Oceny Wyrywkowej

Metody Oceny wywrywkowej © Jan M. Myszewski

2

Ocena wyrywkowa

Problem:

Co można powiedzieć o całej zbiorowości na podstawie
małego jej fragmentu?

Jak zbierać informacje by ryzyko błędnej oceny było najmniejsze?

Jakie jest ryzyko błędnej oceny?

Co to jest błędna ocena?

Co się ocenia?

Jak się to ocenia?

.......

.......

Metody Oceny wywrywkowej © Jan M. Myszewski

3

Ocena wyrywkowa - model

 Zbiorowość składa się z porównywalnych obiektów z których

część ma określoną cech, np. są czarne, a pozostałe tej cechy nie
posiadają

 Nie możliwe jest zbadanie całej zbiorowości – koszt, czas
 Znajomość rozkładu cechy: ilości czarnych jednostek i białych

jednostek ma znaczenie z punktu widzenia decyzji która ma być
podjęta – np. akceptacji zbiorowości

Typowa sytuacja w zarządzaniu jakości:

Partia produktu przed wysłaniem do klienta musi być „zwolniona” -
uznana za akceptowalną.
Status „zwolniona” otrzymuje na podstawie wyniku kontroli jakości
która często nie obejmuje 100% jednostek

Czy taką sytuację spotyka się tylko w procesach produkcyjnych?

Metody Oceny wywrywkowej © Jan M. Myszewski

4

Założenia dotyczące populacji

AQL = dopuszczalny poziom jakości = maksymalna częstość
jednostek "czarnych" w populacji, przy której populacja zostanie
jeszcze uznana za zgodną z oczekiwaniami (z
prawdopodobieństwem 1-PR), przy zastosowaniu danego planu.

LQL = graniczny poziom jakości = minimalna częstość jednostek
"czarnych" w populacji, przy której populacja zostanie uznana za
niezgodną z oczekiwaniami (z prawdopodobieństwem 1-CR), przy
zastosowaniu danego planu.

ω

= częstość jednostek "czarnych" w populacji;

X = liczba jednostek czarnych w próbce

Założenie: Oczekiwania wobec populacji są wyrażone w języku
maksymalnego udziału procentowego

ω

sztuk czarnych w całości

Metody Oceny wywrywkowej © Jan M. Myszewski

5

Sformułowanie hipotezy nt. częstości

Krok 1: sformułuj hipotezę nt. częstości jednostek "czarnych" w
populacji

Warunek "akceptacji" populacji:

ω

≤

AQL

Warunek "odrzucenia" populacji:

ω

≥

LQL

Hipotezy:

H0:

ω

≤

AQL

H1:

ω

≥

LQL

 Kryterium akceptacji hipotezy H0: X

≤

Ac

oczekuje się, że P(X

≤

Ac |

ω

≥

LQL) = CR – odpowiednio mała

liczba

 Kryterium odrzucenia hipotezy H0: X

≥

Re

oczekuje się, że P(X

≥

Re |

ω

≤

AQL) = PR – odpowiednio mała

liczba

Ocenę zgodności populacji z oczekiwaniami dokonuje się poprzez
badanie próbki pobranej z tej populacji i ustalenie ilości X czarnych
sztuk w próbce

Metody Oceny wywrywkowej © Jan M. Myszewski

6

Wybór schematu weryfikacji hipotezy

Krok 2: określ plan badania i liczność próbki

Próbka = jedna lub więcej jednostek losowania pobranych z
populacji i przeznaczonych do dostarczenia informacji o populacji.

Stopień = część próbki, którą trzeba w całości zbadać, by
sformułować decyzję o przyjęciu lub odrzuceniu populacji. W planie
jednostopniowym częścią jest cała próbka.

Plan badania = ściśle określony plan, który wskazuje

 liczbę jednostek wyrobu badanych z każdej populacji (liczność

próbki lub ciąg liczności prób),

 kryteria określania zgodności populacji (liczba kwalifikująca Ac

i liczba dyskwalifikująca Re).

W ostatnim stopniu dowolnego planu: Re = Ac + 1

Liczność próbki jest proporcjonalna do liczności populacji

Metody Oceny wywrywkowej © Jan M. Myszewski

7

Próba losowa

Pobieranie próbki jest losowe = każda jednostka należąca do
populacji ma takie samo prawdopodobieństwo dostania się do
próbki.

Pobieranie próbki jest warstwowe = z każdej warstwy jest
pobierana określona część próbki (podpróbka), składająca się z
co najmniej jednej jednostki.

Jeżeli to uzasadnione, to liczba jednostek w próbce powinna być
pobierana proporcjonalnie do liczności podpartii lub warstw
populacji, rozróżnianych ze względu na pewne racjonalne kryteria.

W przypadku korzystania z losowania warstwowego jednostki z
każdej warstwy powinny być pobierane losowo.

Metody Oceny wywrywkowej © Jan M. Myszewski

8

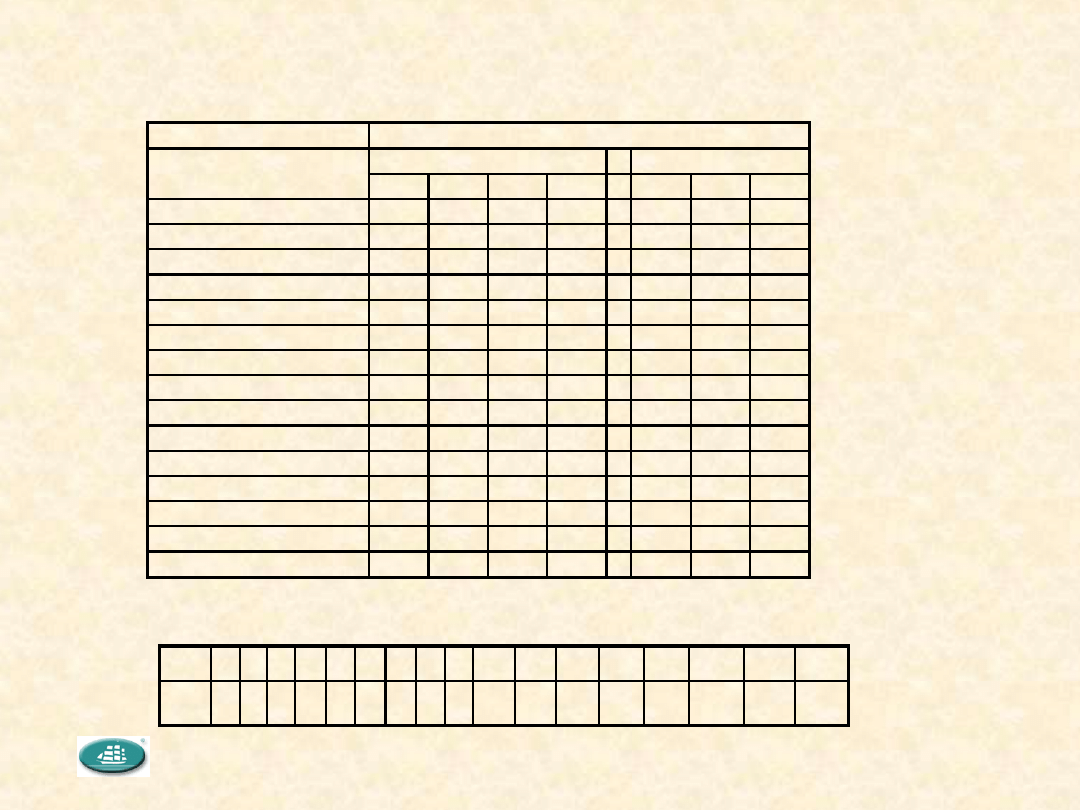
Tabele pomocnicze

Standardowe poziomy kontroli [PN-ISO 2859]

Zakres liczn. populacji

poziomy kontroli

specjalne

ogólne

S1

S2

S3

S4

I

II

III

2

do

8

A

A

A

A

A

A

B

9

do

15

A

A

A

A

A

B

C

16

do

25

A

A

B

B

B

C

D

26

do

50

A

B

B

C

C

D

E

51

do

90

B

B

C

C

C

E

F

91

do

150

B

B

C

D

D

F

G

151

do

280

B

C

D

E

E

G

H

281

do

500

B

C

D

E

F

H

J

501

do

1200

C

C

E

F

G

J

K

1201

do

3200

C

D

E

G

H

K

L

3201

do

10000

C

D

F

G

J

L

M

10001

do

35000

C

D

F

H

K

M

N

35001

do

150000

D

E

G

J

L

N

P

150001

do

500000

D

E

G

J

M

P

Q

500001

i

więcej

D

E

H

K

N

Q

R

Schemat dobierania liczności próbki [PN/N-74-03021]

Kod A B C D E F G H J K L M N P

Q

R

S

liczn. 2 3 5 8 13 20 32 50 80 125 200 315 500 800 1250 2000 3150

Metody Oceny wywrywkowej © Jan M. Myszewski

9

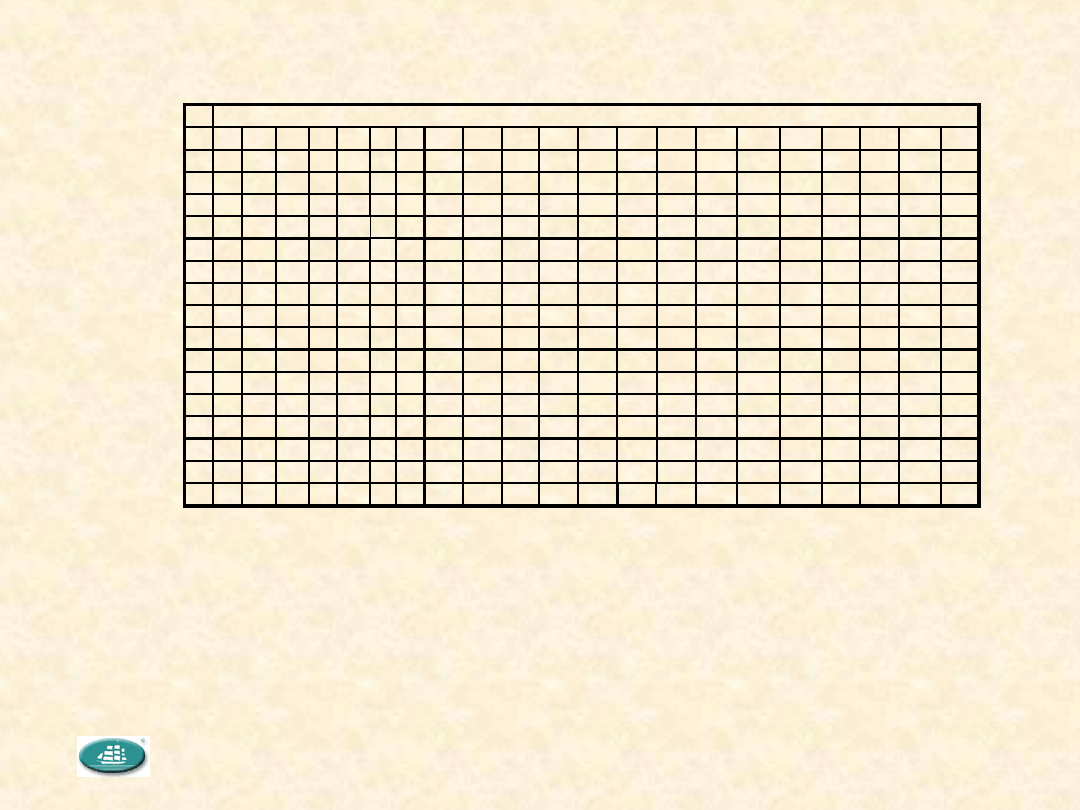
Tabele pomocnicze

AQL

Kod 0.01 0.015 0.025 0.04 0.065 0.1 0.15 0.25 0.40 0.65 1.0

1.5

2.5

4.0

6.5

10

15

25

40

65

100

A

⇓

0-1

⇓

⇓

1-2

2-3

3-4

5-6

B

⇓

0-1

⇑

⇓

1-2

2-3

3-4

5-6

7-8

C

⇓

0-1

⇑

⇓

1-2

2-3

3-4

5-6

7-8 10-11

D

⇓

0-1

⇑

⇓

1-2

2-3

3-4

5-6

7-8 10-11 14-15

E

⇓

0-1

⇑

⇓

1-2

2-3

3-4

5-6

7-8 10-11 14-15 21-22

F

⇓

0-1

⇑

⇓

1-2

2-3

3-4

5-6

7-8 10-11 14-15 21-22

⇑

G

⇓

0-1

⇑

⇓

1-2

2-3

3-4

5-6

7-8 10-11 14-15 21-22

⇑

H

⇓

0-1

⇑

⇓

1-2

2-3

3-4

5-6

7-8 10-11 14-15 21-22

⇑

J

⇓

0-1

⇑

⇓

1-2 2-3

3-4

5-6

7-8 10-11 14-15 21-22

⇑

K

⇓

0-1

⇑

⇓

1-2

2-3 3-4

5-6

7-8 10-11 14-15 21-22

⇑

L

⇓

0-1

⇑

⇓

1-2

2-3

3-4 5-6

7-8 10-11 14-15 21-22

⇑

M

⇓

0-1

⇑

⇓

1-2 2-3

3-4

5-6 7-8 10-11 14-15 21-22

⇑

N

⇓

0-1

⇑

⇓

1-2 2-3 3-4

5-6

7-8 10-11 14-15 21-22

⇑

P

⇓

0-1

⇑

⇓

1-2 2-3 3-4 5-6

7-8 10-11 14-15 21-22

⇑

Q 0-1

⇑

⇓

1-2 2-3 3-4 5-6 7-8 10-11 14-15 21-22

⇑

R

⇑

⇑

1-2 2-3 3-4 5-6 7-8 10-11 14-15 21-22

⇑

⇑

stosować pierwszy plan powyżej strzałki (jeżeli liczność próbki przekracza

liczność partii - stosować kontrolę 100%)

⇓

stosować pierwszy plan poniżej strzałki.

pierwsza liczba Ac, druga liczba Re
AQL wyraża procent jednostek niezgodnych lub liczbę niezgodności przeliczoną
na 100 jednostek produktu

Plany jednostopniowe stosowane podczas kontroli normalnej

(fragment tabl. II-A [PN-ISO

2859-1])

Metody Oceny wywrywkowej © Jan M. Myszewski

10

Weryfikacja hipotezy nt. częstości

Krok 4: przeprowadź wnioskowanie dotyczące zgodności
częstości jednostek "czarnych" w populacji z hipotezą

X

≤

Ac, to

ω

≤

AQL

X

≥

Re, to

ω

≥

LQL

Metody Oceny wywrywkowej © Jan M. Myszewski

11

Ćwiczenia

Ćwiczenie A. Twierdzi się,
że .............................................................. ............................................
....................................................................

Jednostka jest "czarna" gdy ..................................................................
...............................................................................................................

Ćwiczenie B. Sformułuj hipotezę nt. częstości jednostek "czarnych"
w populacji
H0:

ω

≤

AQL = ......

H1:

ω

≥

LQL = ......

Ćwiczenie C. Określ plan badania i liczność próbki
liczność populacji = ...... kod literowy = .....
liczność próbki = ......
Ac = ....
Re = ....

Metody Oceny wywrywkowej © Jan M. Myszewski

12

Ćwiczenia

Ćwiczenie D. Pobierz próbkę i określ liczbę X jednostek "czarnych"
w próbce

X = .......

Ćwiczenie E. Przeprowadź wnioskowanie dotyczące zgodności
częstości jednostek "czarnych" w populacji z hipotezą

Metody Oceny wywrywkowej © Jan M. Myszewski

13

Charakterystyka operacyjna planu badania

0.00001

0.0001

0.001

0.01

0.1

0.9

0.99

0.999

0.9999

0.99999

0.1 0.2

1.0

2.0

10

20 30

Ac = 0 Ac = 1 Ac = 2

λ

P(S Ac)

n

≤

ω

P( )

ω

0

= n

λ

a

ω

a

ω

a

1

ryzyko

dostawcy

ryzyko

odbiorcy

ustalone n

AQL

LQL

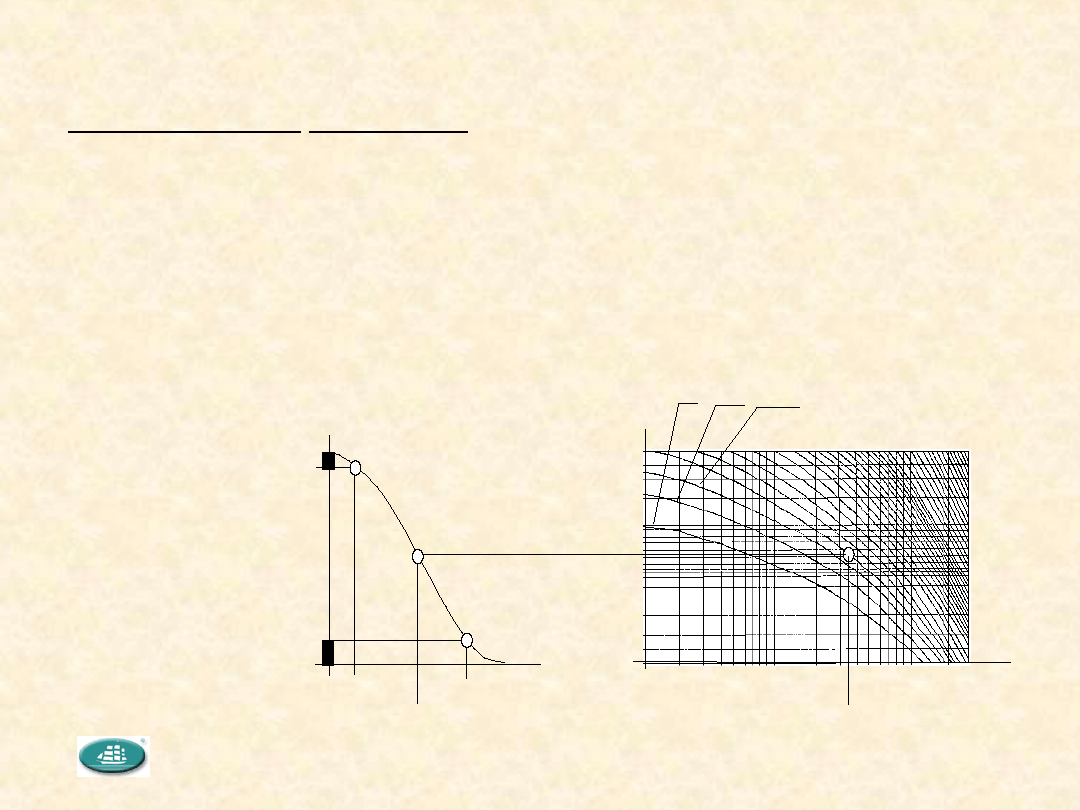
Charakterystyka operacyjna (krzywa operacyjna) planu badania =
funkcja opisująca zależność prawdopodobieństwa przyjęcia partii,
przy postępowaniu zgodnym z danym planem badań, od wadliwości
w partii
P(w) =

Wykreślanie charakterystyki operacyjnej przy pomocy siatki
rozkładu Poissona

∑

≤

≤

Ac

k

0

n

,

P

(k)

ω

Metody Oceny wywrywkowej © Jan M. Myszewski

14

AOQL

Średnia częstość q jednostek "czarnych" po kontroli = oczekiwany
średni poziom częstości jednostek "czarnych" po kontroli dla
danego poziomu częstości jednostek "czarnych" w populacji
przedstawionej do kontroli.

q(

ω

) =

ω

P(

ω

)

AOQL ("graniczna średnia jakość po kontroli") = maksymalna
średnia częstość jednostek "czarnych" po kontroli ze względu na
wszystkie możliwe częstości jednostek "czarnych" w populacjach
przedstawianych do badania, gdy partie wstrzymane zostają
poddane 100% selekcji z zastąpieniem jednostek "czarnych"
jednostkami "białymi"

Metody Oceny wywrywkowej © Jan M. Myszewski

15

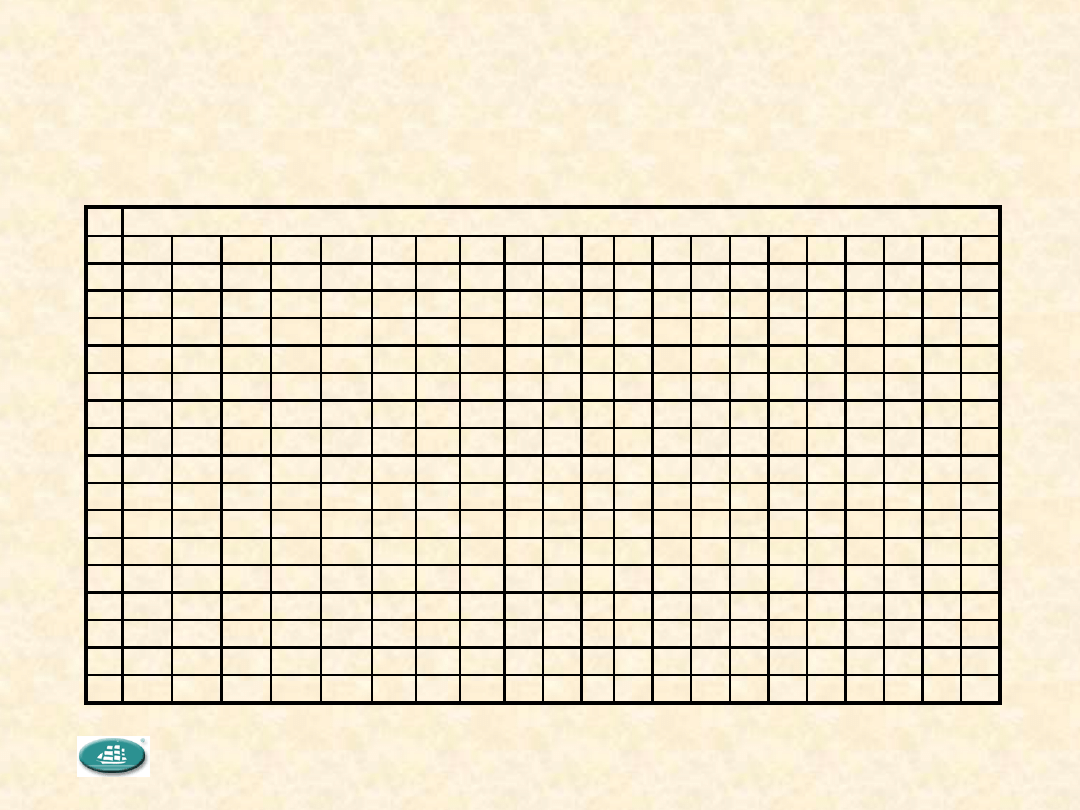
AOQL

AQL

Kod 0.010 0.015 0.025 0.040 0.065 0.10 0.15 0.25 0.40 0.65 1.0 1.5 2.5 4.0 6.5 10 15 25 40 65 100

A

28

42 69 97 160

B

12

28 46 65 110 150

C

7.4

17 27 39 63 90 130

D

4.6

11.0 17 24 40 56 82 120

E

2.8

6.5 11.0 15 24 34 50 72 110

F

AOQL

1.8

4.2 6.9 9.7 16 22 33 47 73

G

1.2

2.6 4.3 6.1 9.9 14 21 29 46

H

0.74

1.7 2.7 3.9 6.3 9.0 13 19 29

J

0.46

1.10 1.7 2.4 4.0 5.6 8.2 12 18

K

0.29

0.67 1.10 1.6 2.5 3.6 5.2 7.5 12

L

0.18

0.42 0.69 0.97 1.6 2.2 3.3 4.7 7.3

M

0.12

0.27 0.44 0.62 1.00 1.4 2.1 3.0 4.7

N

0.074

0.17 0.27 0.39 0.63 0.90 1.3 1.9 2.9

P

0.046

0.11 0.17 0.24 0.40 0.56 0.82 1.2 1.8

Q 0.029

0.067 0.11 0.16 0.25 0.36 0.52 0.75 1.2

R

0.042 0.069 0.097 0.16 0.22 0.33 0.47 0.73

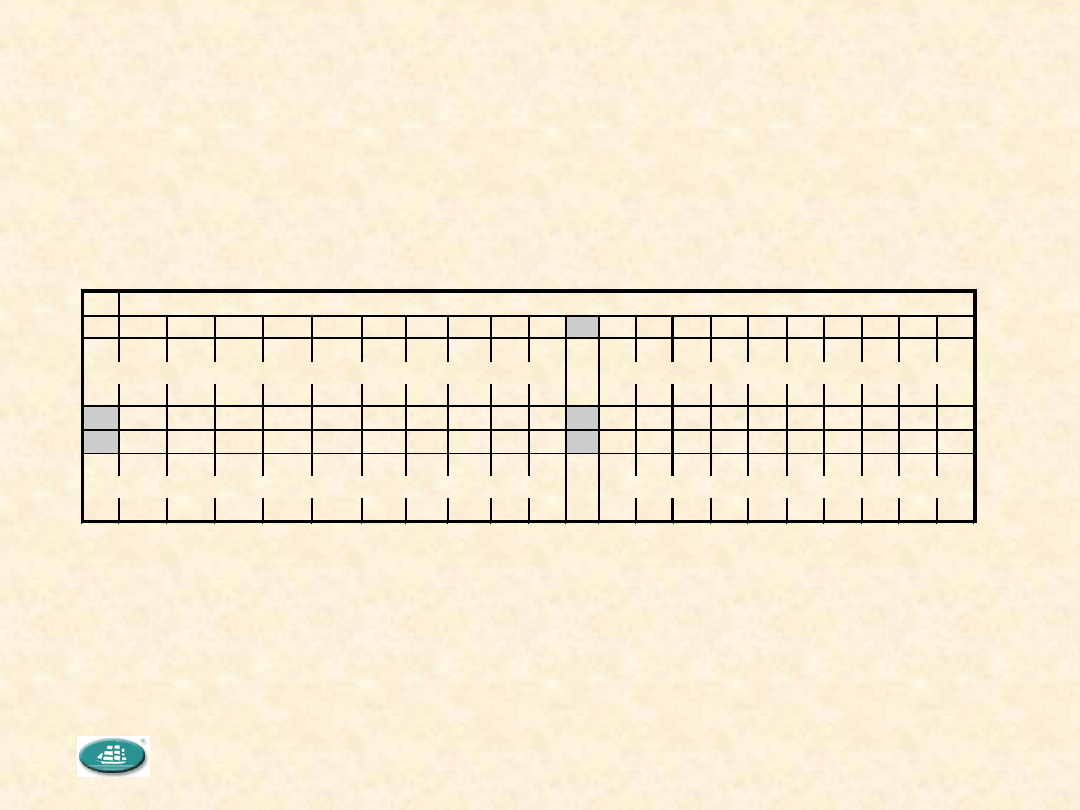
Tabela wartości AOQL w zależności od AQL i liczności próbki

(fragment tabl.

V-A [PN-ISO 2859-1])

Metody Oceny wywrywkowej © Jan M. Myszewski

16

AOQL

Podanie wartości Ac i AOQL jednoznacznie identyfikuje krzywą

operacyjną planu badań i jednocześnie charakteryzuje skuteczność badań

w sposób niezależny od częstości jednostek "czarnych" w badanych

populacjach.

Przykład: Na podstawie AOQL = 1.7 odczytujemy AQL = 1.0 oraz kody

literowe liczności próbki: H = 50 lub J = 80 (patrz rysunek poniżej).

Dla ustalonej wartości Ac odczytujemy z tabeli planu jednostopniowego
stosowanego podczas kontroli normalnej, że np. :
dla Ac = 1, taki plan kontroli odpowiada liczności próbki H = 50,
zaś dla Ac = 0 zastosowanie któregokolwiek planu kontroli (o danych
licznościach) wymagało przyjęcia niższego AQL (0.25 dla H, 0.15 dla J) i
spowoduje, niższą wartość AOQL - odpowiednio 0.74 lub 0.46.

AQL

Kod 0.010 0.015 0.025 0.040 0.065 0.10 0.15 0.25 0.40 0.65 1.0 1.5 2.5 4.0 6.5 10

15

25

40

65 100

A

28

42

69

97

160

G

1.2

2.6 4.3 6.1 9.9 14

21

29

46

H

0.74

1.7 2.7 3.9 6.3 9.0 13

19

29

J

0.46

1.10 1.7 2.4 4.0 5.6 8.2 12

18

K

0.29

0.67 1.10 1.6 2.5 3.6 5.2 7.5 12

R

0.042 0.069 0.097 0.16 0.22 0.33 0.47 0.73

Metody Oceny wywrywkowej © Jan M. Myszewski

17

Twierdzenie "brak jednostek czarnych"

Twierdzi się, że w populacji brak jest jednostek "czarnych" czyli,
że

ω

= 0.

Przyjmujemy AQL = 0, a zatem Ac = 0.

LQL określa się na podstawie liczności populacji.

Jeżeli X = 0,

to brak podstaw do odrzucenia hipotezy H0

Jeżeli X > 0,

to są podstawy do przyjęcia hipotezy H1

Tw. Im liczniejsza próbka tym mniejsza wartość LQL.

Metody Oceny wywrywkowej © Jan M. Myszewski

18

Tabele pomocnicze

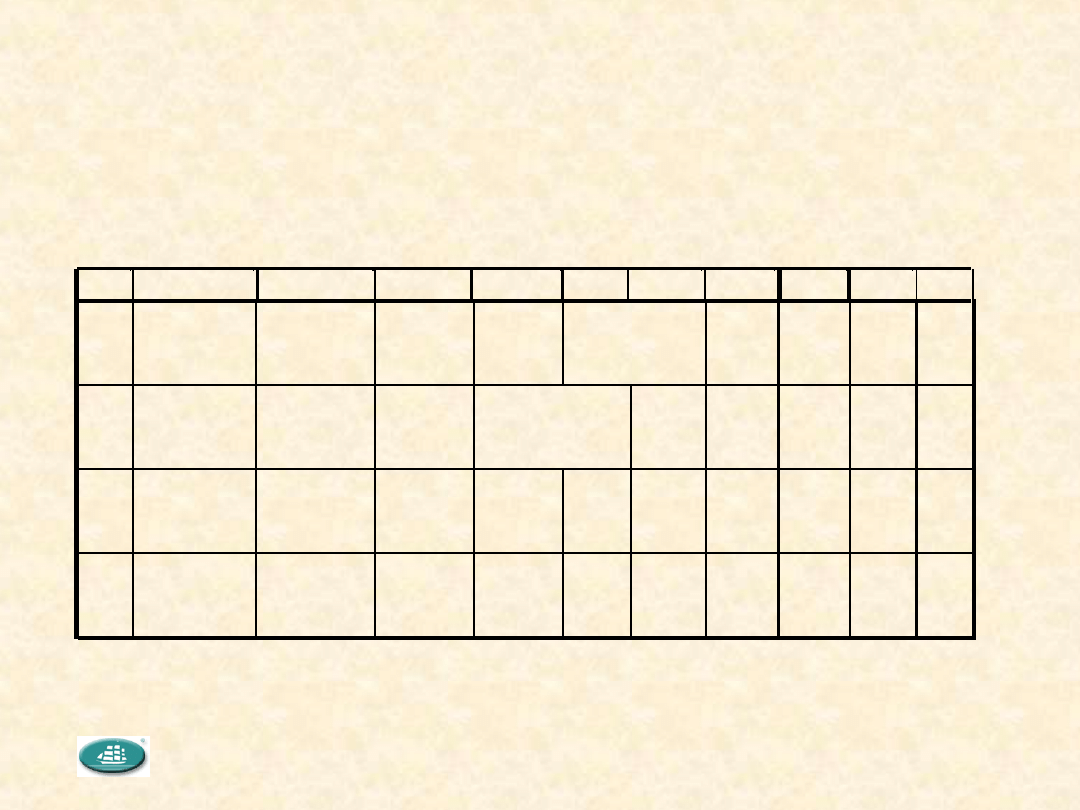
Tabela liczności populacji i prób zapewniających odpowiednie
poziomy LQ.

(Fragment tab. D.2 [PN-ISO 2859-2])

LQ

0.5

0.8

1.25

2

3.15

5

8

12.5

20

32

liczn.

K

K

E E

prób. 380

380

255

255 170 170 125 125

17 17 13 13 9 9 6 6

popul 501 1200 501 1200 501 1200 501 1200

16 25 16 25 16 25 16 25

L

L

prób. 430

430

280

280 200 200

28 28 22 22 15 15 10 10 6 6

popul 1201 3200 1201 3200 1201 3200

26 50 26 50 26 50 26 50 26 50

M

M

H

H

D D

prób. 450

450

315

315

50 50 44 44 34 34 24 24 16 16 10 10 8 8

popul 3200 10000 3200 1000 0

51 90 51 90 51 90 51 90 51 90 51 90 51 90

N

N

J

J

E E

prób. 500

500

90

90 80 80 55 55 38 38 26 26 18 18 13 13

popul

10001

35000

91 150 91 150 91 150 91 150 91 150 91 150 91 150

Metody Oceny wywrywkowej © Jan M. Myszewski

19

Ćwiczenia

Ćwiczenie A. Twierdzi się,
że .............................................................. ..............................................
...................................................................

Jednostka jest "czarna" gdy ..................................................................
...............................................................................................................

Ćwiczenie B. Sformułuj hipotezę nt. częstości jednostek "czarnych" w
populacji

H0:

ω

= ......

H1:

ω

> ......

Ćwiczenie C. Określ plan badania i liczność próbki
liczność populacji = ...... kod literowy = .....
liczność próbki = ......
Ac = ....
Re = ....

Metody Oceny wywrywkowej © Jan M. Myszewski

20

Ćwiczenia

Ćwiczenie D. Pobierz próbkę i określ liczbę X jednostek "czarnych"
w próbce

X = .......

Ćwiczenie E. Przeprowadź wnioskowanie dotyczące zgodności
częstości jednostek "czarnych" w populacji z hipotezą

Metody Oceny wywrywkowej © Jan M. Myszewski

21

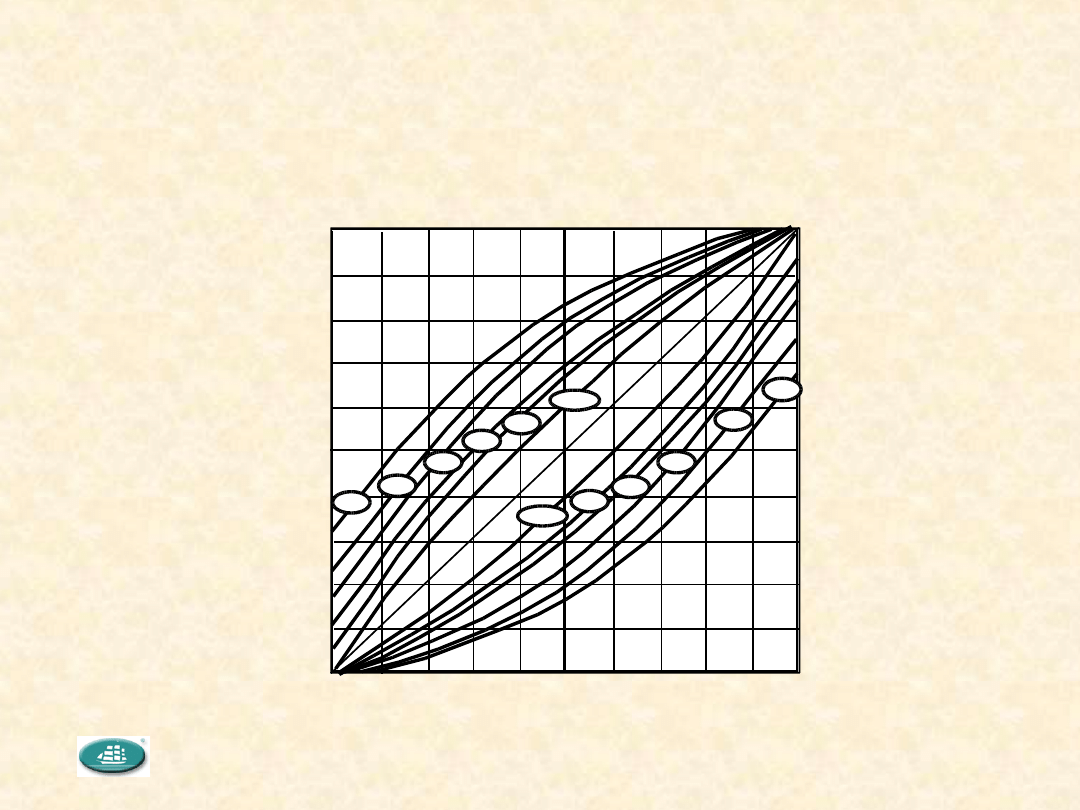
Przedziałowe szacowanie częstości

ω

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

1.0

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

0.0

p

ω

10

10

15

15

20

20

30

30

50

50

100

100

Jeżeli p jest częstością jednostek "czarnych" w próbce n elementowej, to
granice 95-procentowego przedziału ufności dla częstości

ω

jednostek

"czarnych" w populacji można odczytać z poniższego nomogramu

Metody Oceny wywrywkowej © Jan M. Myszewski

22

Jakość szacowania częstości

ω

Badamy częstość

ω

jednostek "czarnych" w populacji

1. Jeżeli na podstawie analizy próbki losowej prostej o liczności n
mamy oszacować częstość z dokładnością do k cyfr po przecinku, tzn.

ω

=

ω

1

10

-1

+...+

ω

k

10

-k

,

0

Ł

ω

i

Ł 9,

to
n

ł (1.96

⋅

10k )2

ω⋅

(1-

ω

)

W 95 przypadkach na 100 częstość empiryczna otrzymana na
podstawie analizy próbki o takiej liczności da wynik spełniający
założenia

Metody Oceny wywrywkowej © Jan M. Myszewski

23

Jakość szacowania częstości

ω

2. Jeżeli szacowana częstość

ω

jest bliska zeru (lub 1-

ω

jest bliska

zeru) - np. 10

m

⋅

ω

=

ω

0

∈

[1,10),

to liczba cyfr znaczących k oszacowania na podstawie próbki powinna
być nie mniejsza niż m i wtedy
n

ł 1.96

2

⋅

10

m+1

3. Jeżeli rząd wielkości

ω

nie jest znany, to do oszacowania częstości

na podstawie próbki losowej należy przyjąć liczność

n

ł 0.98

2

× 10

2k

.

Metody Oceny wywrywkowej © Jan M. Myszewski

24

a. Przyjmij (orientacyjną) liczność populacji wyników których dotyczyć

będzie analiza wyrywkowa - zakładając, że składa się ona z tych
których nie zbadano a powstały w ustalonym przedziale czasu
współczesnym np z tymi, które już zostały zbadane w zadaniu 1.

b. Postaw hipotezę odnośnie frakcji jednostek niezgodnych w populacji,

kierując się np. wynikami zgromadzonymi w zadaniu 1.

c. Zaplanuj schemat kontroli - wskaż krzywą operacyjną planu kontroli

d. Pobierz próbkę o odpowiedniej liczności i określ liczbę niegodności w

próbce

e. Posługując się tabelami, zweryfikuj hipotezę dotyczącą frakcji wyników

niezgodnych postawioną wcześniej

f. Oszacuj ilość niezgodności w całej zbiorowości

Ćwiczenia