OBCIĄśENIA W UKŁADZIE

KORBOWO-TŁOKOWYM

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Wiadomości wstępne

Okresy zmienno

ś

ci obci

ąż

e

ń

:

- dla sił gazowych: połowa cz

ę

stotliwo

ś

ci obrotów wału korbowego (odpowiada

przedziałowi 0÷720°);

- dla sił bezwładno

ś

ci: cz

ę

stotliwo

ść

obrotów wału korbowego (odpowiada

przedziałowi 0÷360°).

Obci

ąż

enia wyst

ę

puj

ą

ce w układzie korbowym wynikaj

ą

z jednoczesnego działania

sił gazowych i sił bezwładno

ś

ci.

Siły działaj

ą

ce na tłok maj

ą

jednakowy kierunek i mog

ą

by

ć

sumowane

algebraicznie (z uwzgl

ę

dnieniem znaków zwi

ą

zanych z aktualnym zwrotem ich

działania, zale

ż

nym od k

ą

ta obrotu wału korbowego).

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Wiadomości wstępne

Transformacj

ę

wykresu indykatorowego na układ współrz

ę

dnych p-

α

umo

ż

liwia

oczywista równo

ść

:

Zmienno

ść

siły gazowej działaj

ą

cej na tłok wynika ze zmienno

ś

ci ci

ś

nienia w

cylindrze – przedstawianej w postaci wykresu we współrz

ę

dnych p-V (wykres

indykatorowy. Analiz

ę

obci

ąż

e

ń

(siły gazowe, siły bezwładno

ś

ci ) przeprowadza si

ę

zwykle w zale

ż

no

ś

ci od k

ą

ta obrotu wału korbowego

α

.

(

)

(

)

(

)

2

2

4

1 cos

1 cos 2

4

V

V

s

R

D

λ

α

α

π

−





=

=

−

+

−









Po prostym przekształceniu:

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Wiadomości wstępne

Dla kolejnych warto

ś

ci

α

oblicza si

ę

V i z wykresu indykatorowego odczytuje si

ę

warto

ść

ci

ś

nienia w cylindrze p, co w rezultacie umo

ż

liwia wykre

ś

lenie zale

ż

no

ś

ci

p=p(

α

).

(

)

(

)

2

2

1 cos

1 cos 2

4

4

D

V

V

R

π

λ

α

α





= +

−

+

−









Siła gazowa działaj

ą

ca na tłok zale

ż

y od ci

ś

nienia w cylindrze:

(

)

2

4

G

H

D

F

p

p

π

=

−

Siła bezwładno

ś

ci zmienia si

ę

tak jak przyspieszenie:

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Wiadomości wstępne

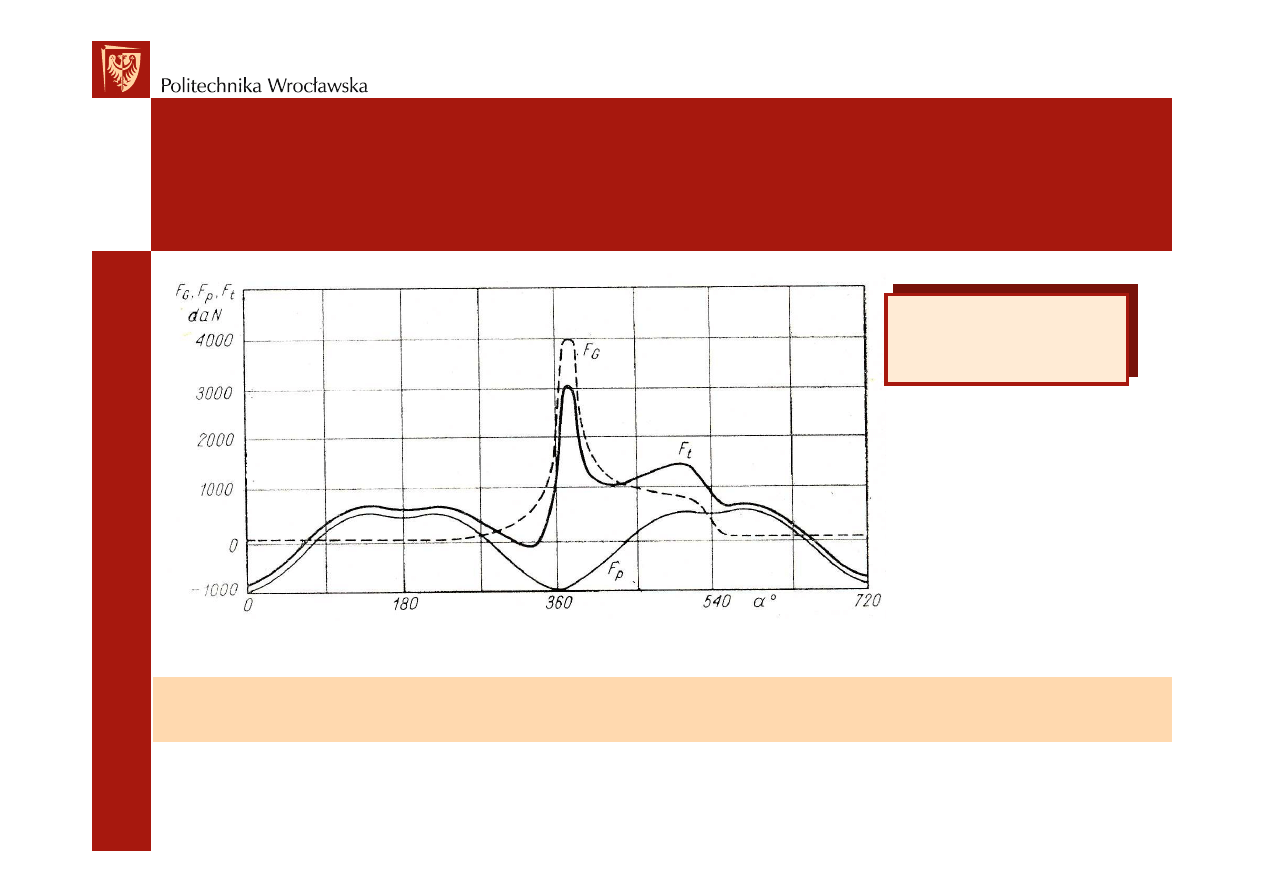
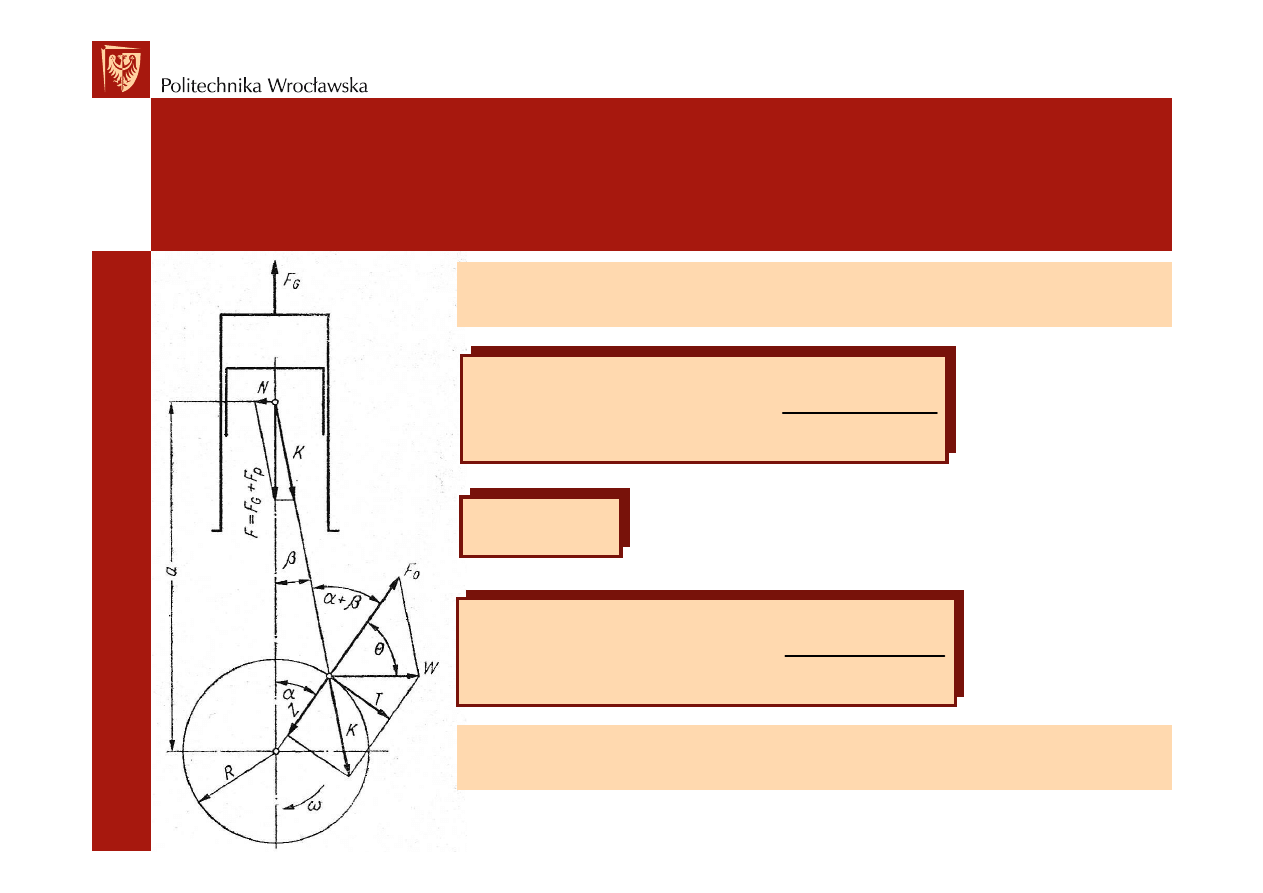
F

G

– siła gazowa, F

p

– siła bezwładno

ś

ci, F

t

– siła wypadkowa

Jako dodatni przyj

ę

to

zwrot wywołuj

ą

cy

ś

ciskanie korbowodu.

Jako dodatni przyj

ę

to

zwrot wywołuj

ą

cy

ś

ciskanie korbowodu.

Siła bezwładno

ś

ci zmniejsza maksymalne obci

ąż

enia działaj

ą

ce na tłok w kierunku

osi cylindra.

m

kp

m

ko

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

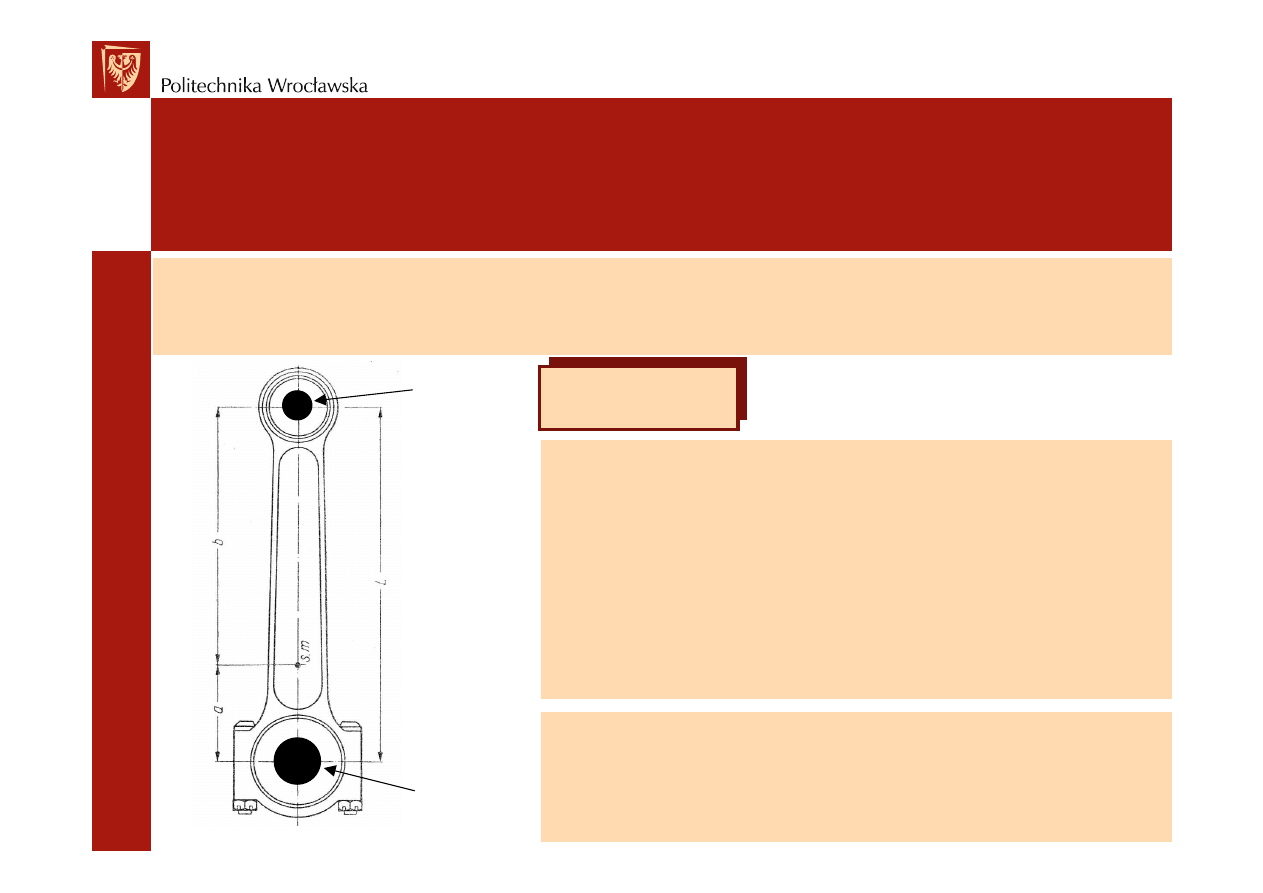
Korbowód zredukowany

Zło

ż

ony ruch korbowodu (ruch posuwisto-zwrotny oraz ruch obrotowy) utrudnia

analiz

ę

jego obci

ąż

e

ń

. W praktyce in

ż

ynierskiej stosuje si

ę

przybli

ż

on

ą

metod

ę

analizy korbowodu zredukowanego.

k

kp

ko

m

m

m

=

+

m

k

– masa korbowodu;

m

kp

– cz

ęść

masy korbowodu zredukowana do osi

sworznia tłoka poruszaj

ą

ca si

ę

ruchem posuwisto-

zwrotnym (masa posuwista);

m

ko

– cz

ęść

masy korbowodu zredukowana do osi

czopa korbowego wału wykonuj

ą

ca ruch obrotowy

(masa obrotowa)

Dynamiczn

ą

równowa

ż

no

ść

korbowodu

rzeczywistego i zredukowanego zapewnia ponadto
pokrywanie si

ę ś

rodka masy korbowodu i

ś

rodka

masy zło

ż

enia (układu) mas zredukowanych.

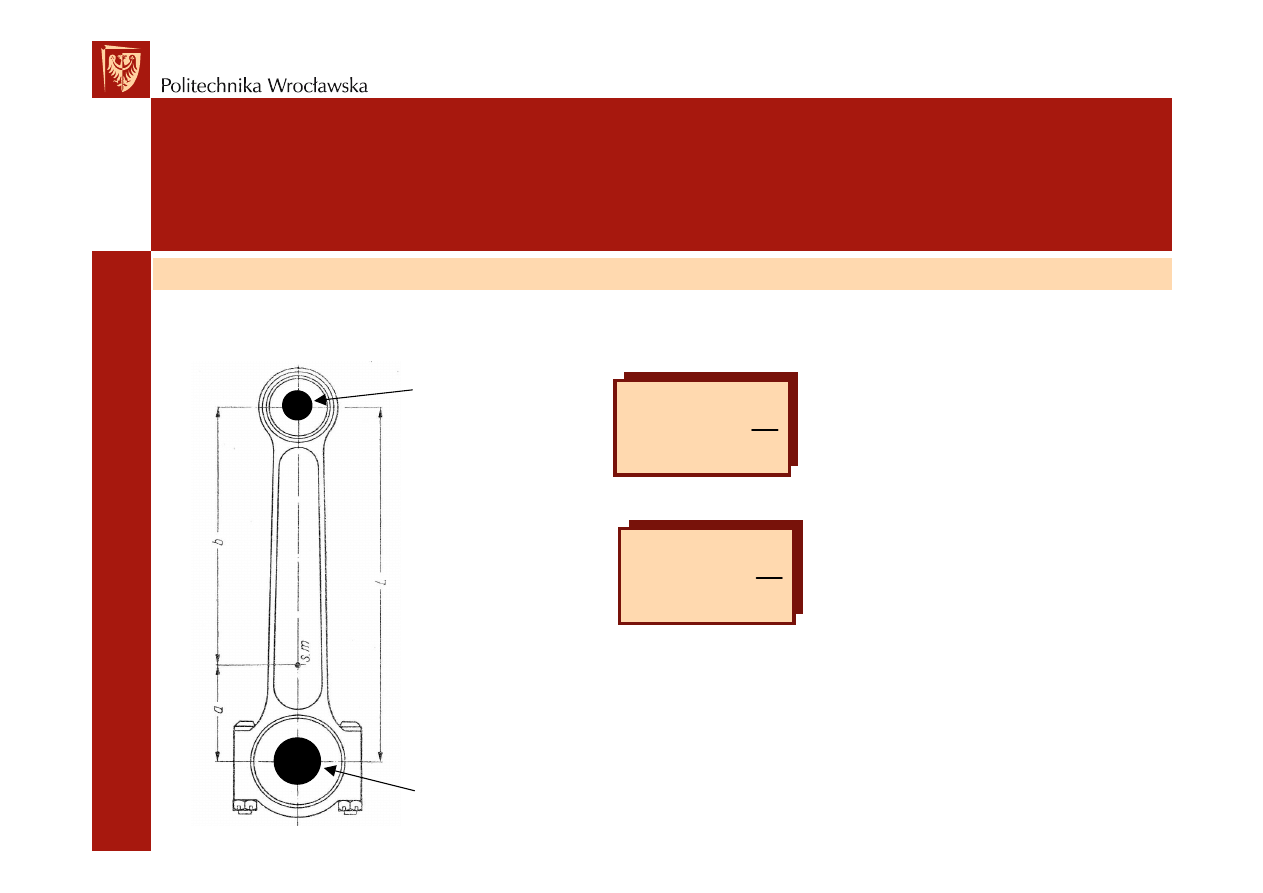
OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

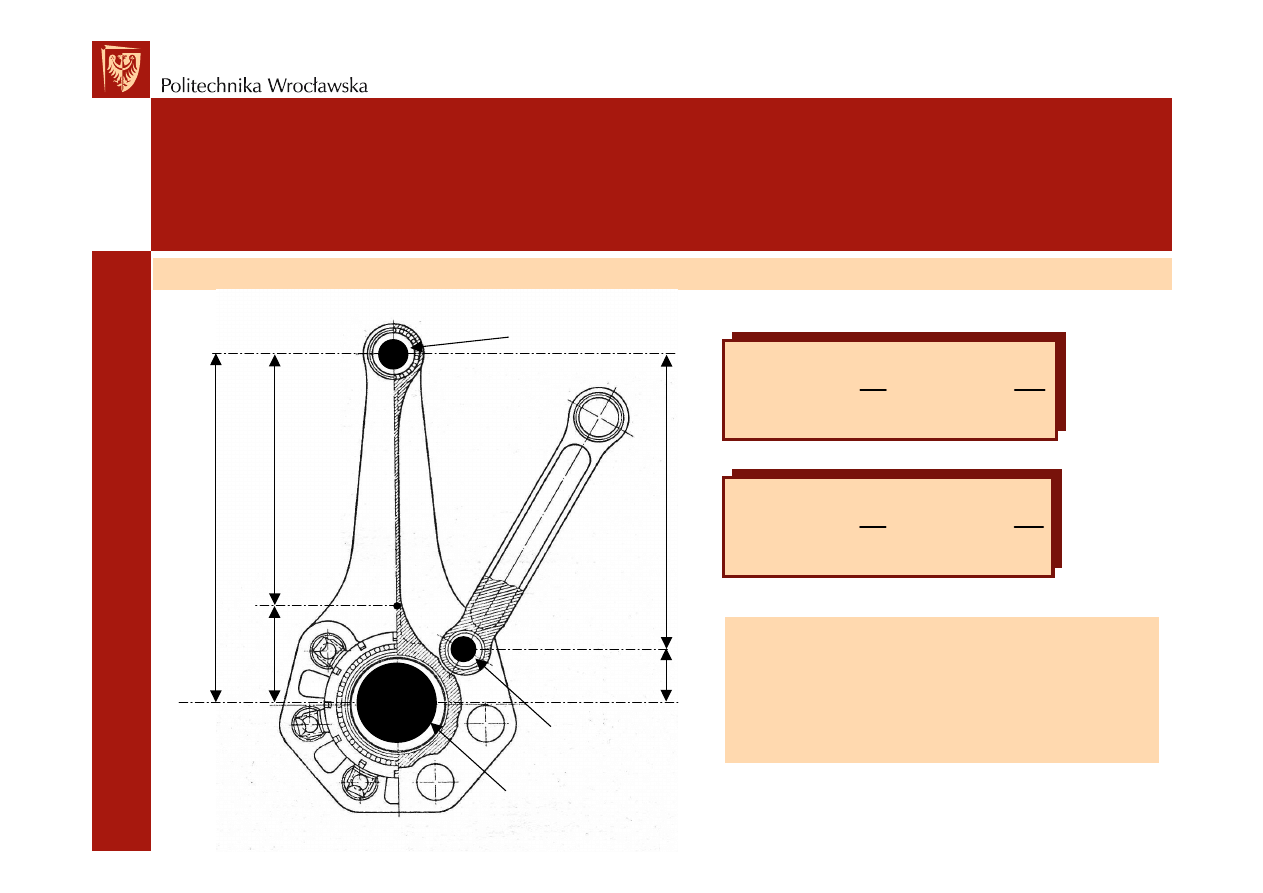
Korbowód zredukowany

Masy zast

ę

pcze oblicza si

ę

ze wzorów:

m

kp

m

ko

kp

k

a

m

m

L

=

⋅

ko

k

b

m

m

L

=

⋅

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

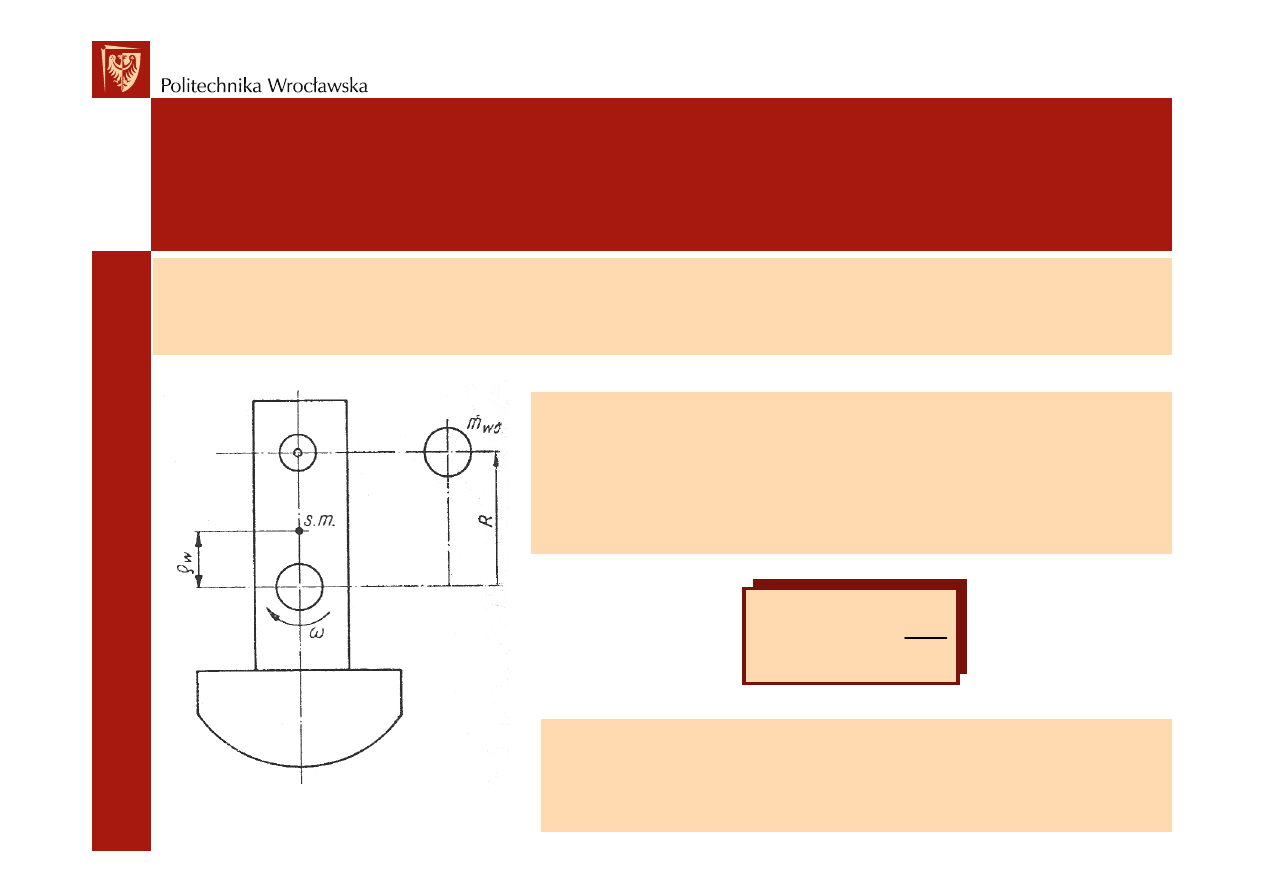
Korbowód zredukowany

Masy zast

ę

pcze korbowodu głównego silnika gwiazdowego oblicza si

ę

ze wzorów:

1

1

i

kp

k

ko

a

a

m

m

m

L

L

−

′

′

=

⋅ +

⋅

∑

m

kp

m

ko

a

b

L

b

’

a

’

m’

ko

1

1

i

ko

k

ko

b

b

m

m

m

L

L

−

′

′

=

⋅ +

⋅

∑

m’

ko

– cz

ęść

masy korbowodu

bocznego wykonuj

ą

ca ruch

obrotowy;

i – liczba korbowodów bocznych.

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Korbowód zredukowany

Masa wykonuj

ą

ca ruch posuwisto zwrotny m

p

w układzie korbowym składa si

ę

z

masy tłoka kompletnego m

t

i masy korbowodu zredukowanej do osi sworznia

tłokowego m

kp

.

w

wo

w rz

m

m

R

ρ

=

⋅

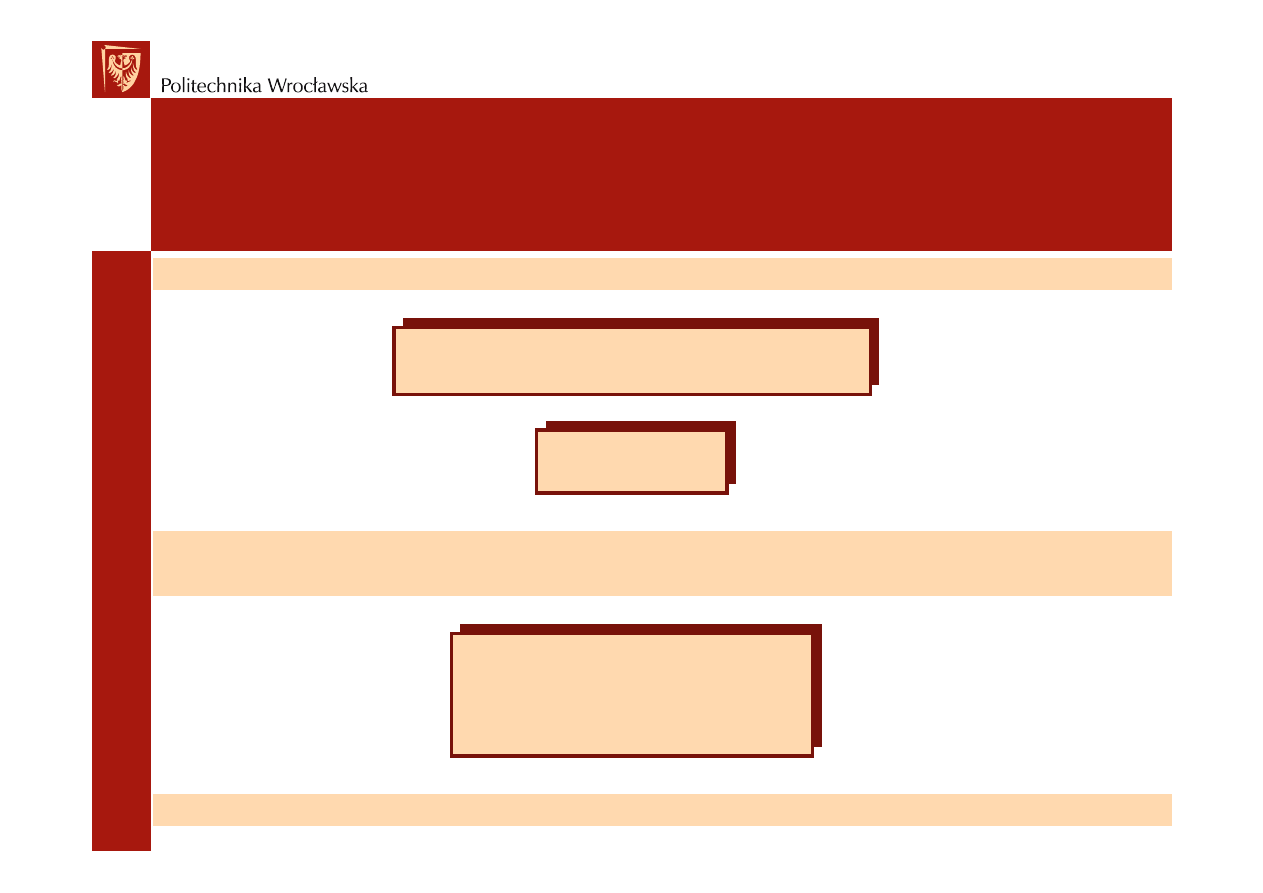
Masa wykonuj

ą

ca ruch obrotowy w układzie

korbowym jest sum

ą

masy wykorbienia m

w rz

wału i

masy korbowodu zredukowanej do osi czopa
korbowego m

ko

. Mas

ę

wykorbienia redukuje si

ę

do

osi czopa korbowego wg zale

ż

no

ś

ci:

m

wo

– masa wykorbienia zredukowana do osi czopa

korbowego;

m

w rz

– rzeczywista masa wykorbienia

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Siły masowe (bezwładności)

Siła bezwładno

ś

ci działaj

ą

ca na masy znajduj

ą

ce si

ę

w ruchu posuwisto zwrotnym:

p

t

kp

m

m

m

=

+

Sił

ę

bezwładno

ś

ci działaj

ą

c

ą

na masy znajduj

ą

ce si

ę

w ruchu posuwisto zwrotnym

mo

ż

na wyrazi

ć

jako sum

ę

siły masowej pierwszego i drugiego rz

ę

du:

(

)

2

cos

cos 2

p

p

F

m

R

ω

α λ

α

= −

⋅ ⋅

+ ⋅

2

2

cos

cos 2

pI

p

pII

p

F

m

R

F

m

R

ω

α

ω λ

α

= −

⋅ ⋅

⋅

= −

⋅ ⋅

⋅

Powy

ż

sze zale

ż

no

ś

ci wykorzystuje si

ę

w analizie wyrównowa

ż

enia silnika.

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Siły masowe (bezwładności)

Siła bezwładno

ś

ci mas wiruj

ą

cych w układzie korbowym:

0

ko

wo

m

m

m

=

+

2

o

o

F

m

R

ω

= − ⋅ ⋅

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

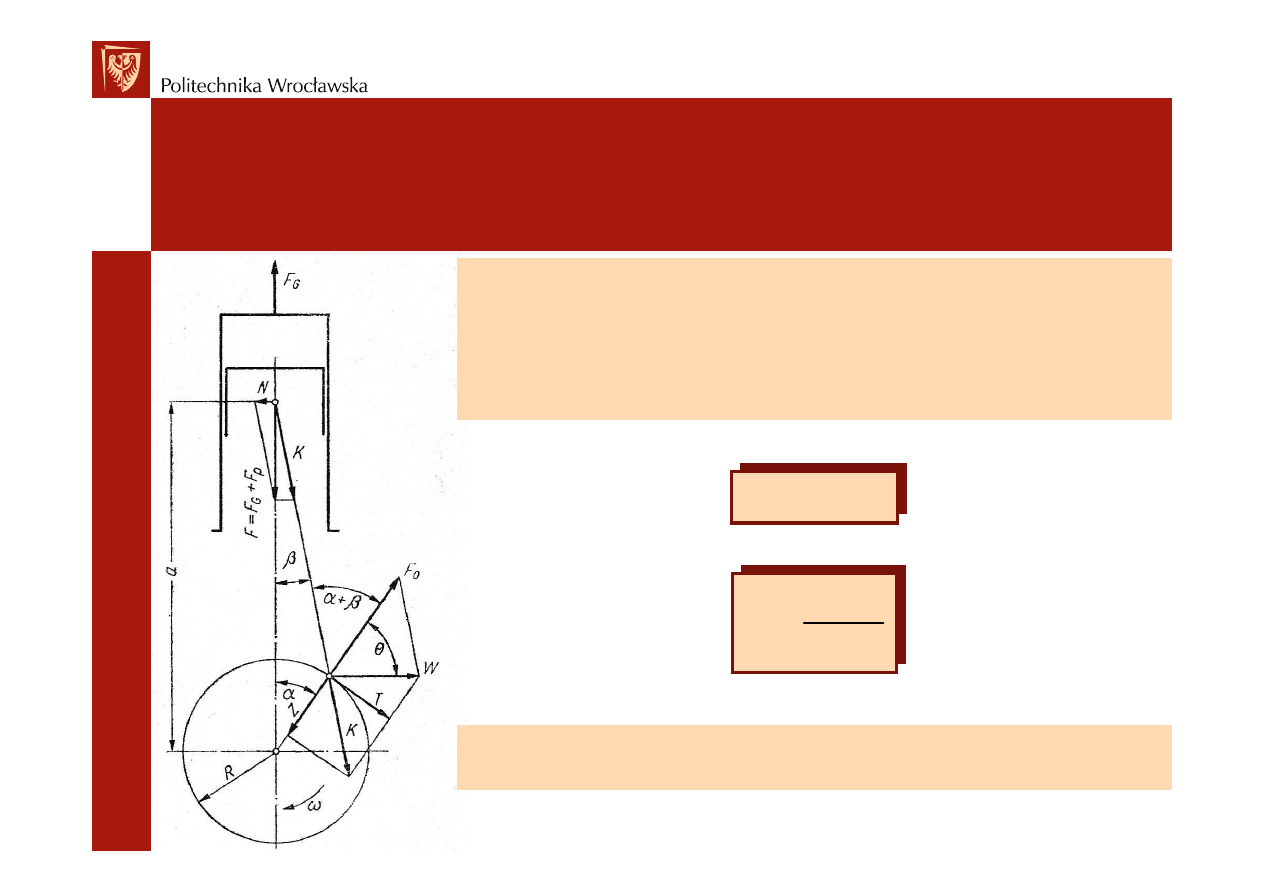
Rozkład obciążeń w układzie korbowym

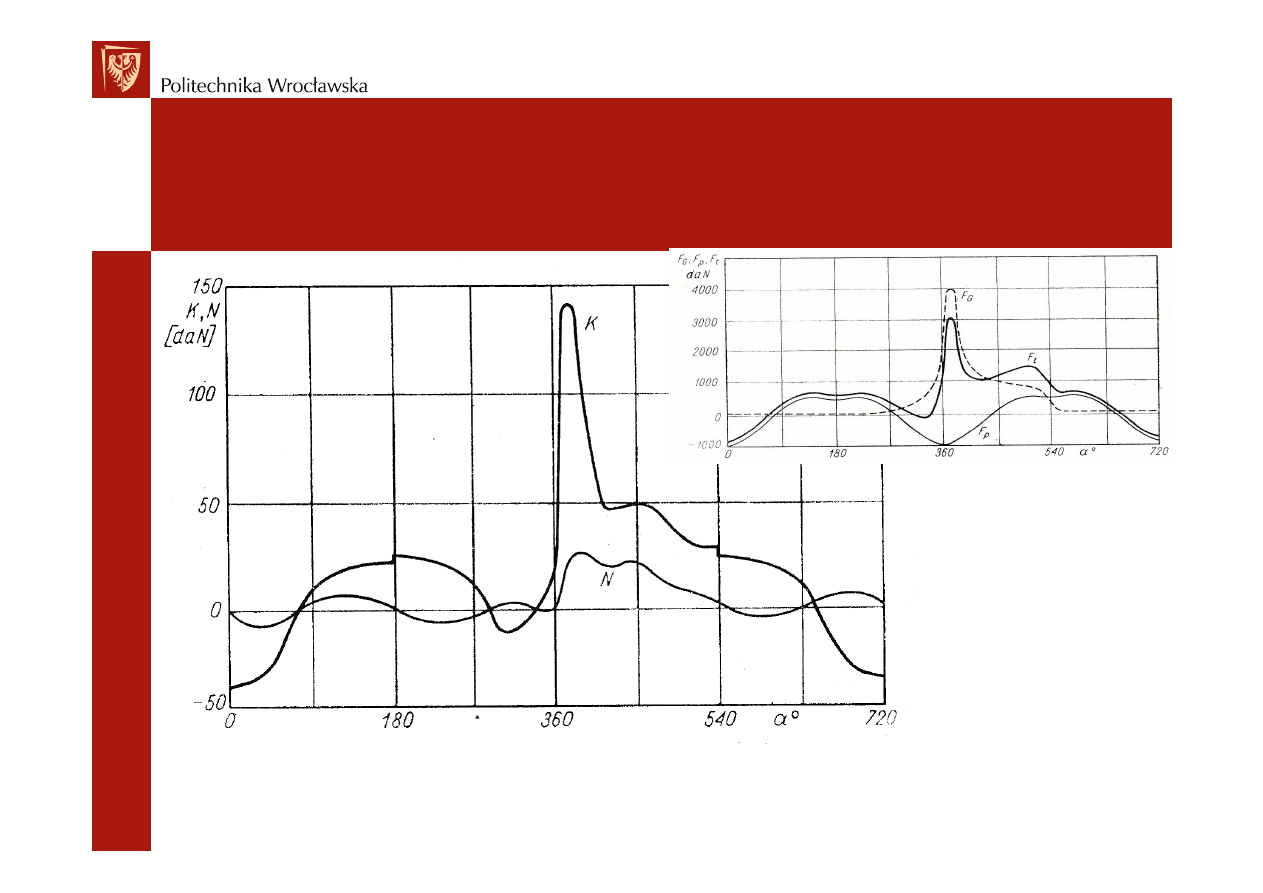
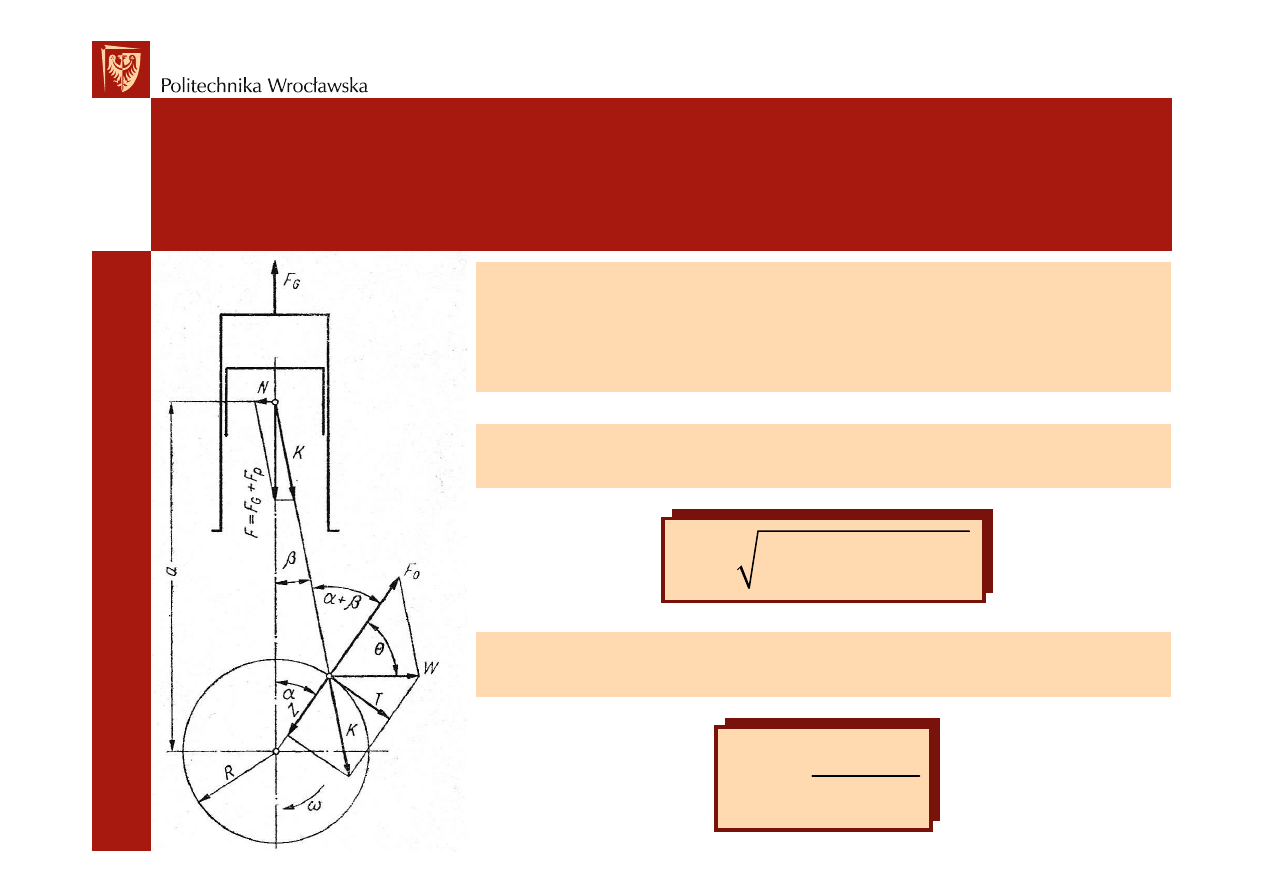
Wypadkowa siła F działaj

ą

ca na masy znajduj

ą

ce si

ę

w

ruchu posuwisto zwrotnym rozkłada si

ę

na składow

ą

N

(prostopadł

ą

do osi cylindra i charakteryzuj

ą

c

ą

nacisk

tłoka na tulej

ę

cylindra) oraz sił

ę

K (obci

ąż

aj

ą

c

ą

wzdłu

ż

nie

korbowód):

N

F tg

β

= ⋅

cos

F

K

β

=

Przykładowe przebiegi składowych N i K przedstawia
wykres:

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

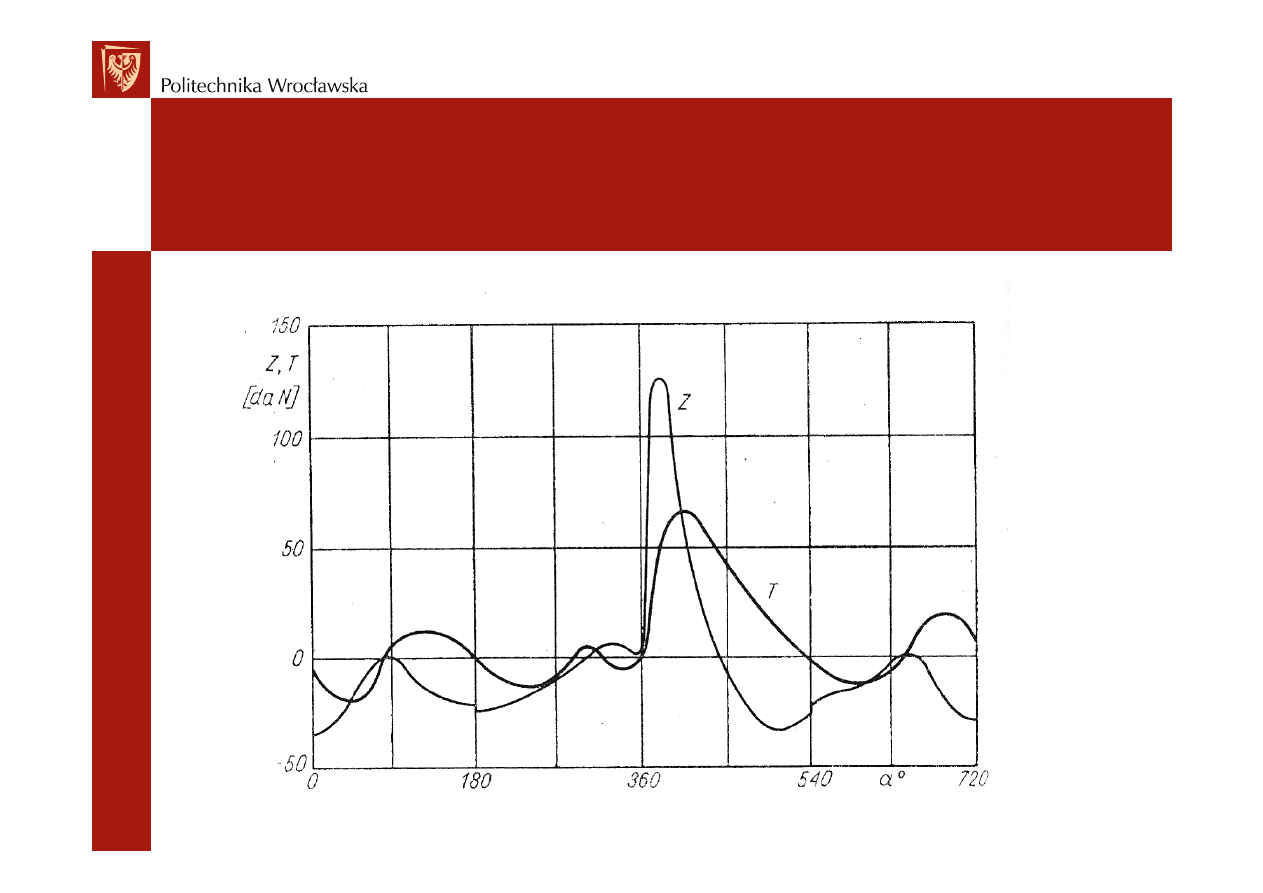
Siła K przejmowana jest przez wykorbienie wału. Jej
składowa T wywołuje moment obrotowy silnika M

o

.

(

)

(

)

sin

sin

cos

T

K

F

α β

α β

β

+

= ⋅

+

=

Przykładowe przebiegi składowych T i Z przedstawia
wykres:

(

)

(

)

cos

cos

cos

Z

K

F

α β

α β

β

+

= ⋅

+

=

o

M

T R

= ⋅

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

Obci

ąż

enia działaj

ą

ce na układ korbowy silnika wielocylindrowego (gwiazdowego)

s

ą

do

ść

zło

ż

one w zwi

ą

zku z sumowaniem si

ę

obci

ąż

e

ń

od poszczególnych

zespołów tłok-korbowód.

Je

ż

eli wykorbienie wału współpracuje z dwoma lub wi

ę

ksz

ą

liczb

ą

korbowodów, to

wielko

ść

i przebieg zmian działaj

ą

cych na to wykorbienie obci

ąż

e

ń

zale

ż

y od

ustawienia cylindrów i kolejno

ś

ci ich pracy (zapłonów).

Całkowite obci

ąż

enie działaj

ą

ce na wykorbienie jest sum

ą

obci

ąż

e

ń

przejmowanych

od poszczególnych zespołów tłok-korbowód, zmieniaj

ą

cych si

ę

podobnie lecz z

odpowiednimi przesuni

ę

ciami fazowymi, przy czym ró

ż

nice wynikaj

ą

ce z kinematyki

korbowodów bocznych w silnikach gwiazdowych nie maj

ą

istotnego znaczenia.

Siły styczne T oraz normalne Z obci

ąż

aj

ą

ce wał korbowy mo

ż

na zatem sumowa

ć

algebraicznie, uwzgl

ę

dniaj

ą

c przesuni

ę

cia fazowe wynikaj

ą

ce z kolejno

ś

ci pracy

cylindrów.

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

Dobieraj

ą

c kolejno

ść

pracy cylindrów silnika czterosuwowego nale

ż

y kierowa

ć

si

ę

nast

ę

puj

ą

cymi wskazówkami.

1. W czasie dwóch obrotów wału korbowego (

α

= 0÷720°) w ka

ż

dym cylindrze

zachodzi spalanie mieszanki i rozpr

ęż

anie spalin. Najmniejsze nierównomierno

ś

ci

momentu obrotowego wyst

ą

pi

ą

przy jednakowych odst

ę

pach fazowych w pracy

poszczególnych cylindrów, charakteryzowanych przez tzw. k

ą

t fazowy

γ

:

720

i

γ

=

γ

– k

ą

t obrotu wału korbowego w czasie dziel

ą

cym zapłon mieszanki w dwóch

cylindrach, s

ą

siednich ze wzgl

ę

du na kolejno

ść

ich pracy;

i – liczba cylindrów silnika.

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

Dobieraj

ą

c kolejno

ść

pracy cylindrów silnika czterosuwowego nale

ż

y kierowa

ć

si

ę

nast

ę

puj

ą

cymi wskazówkami.

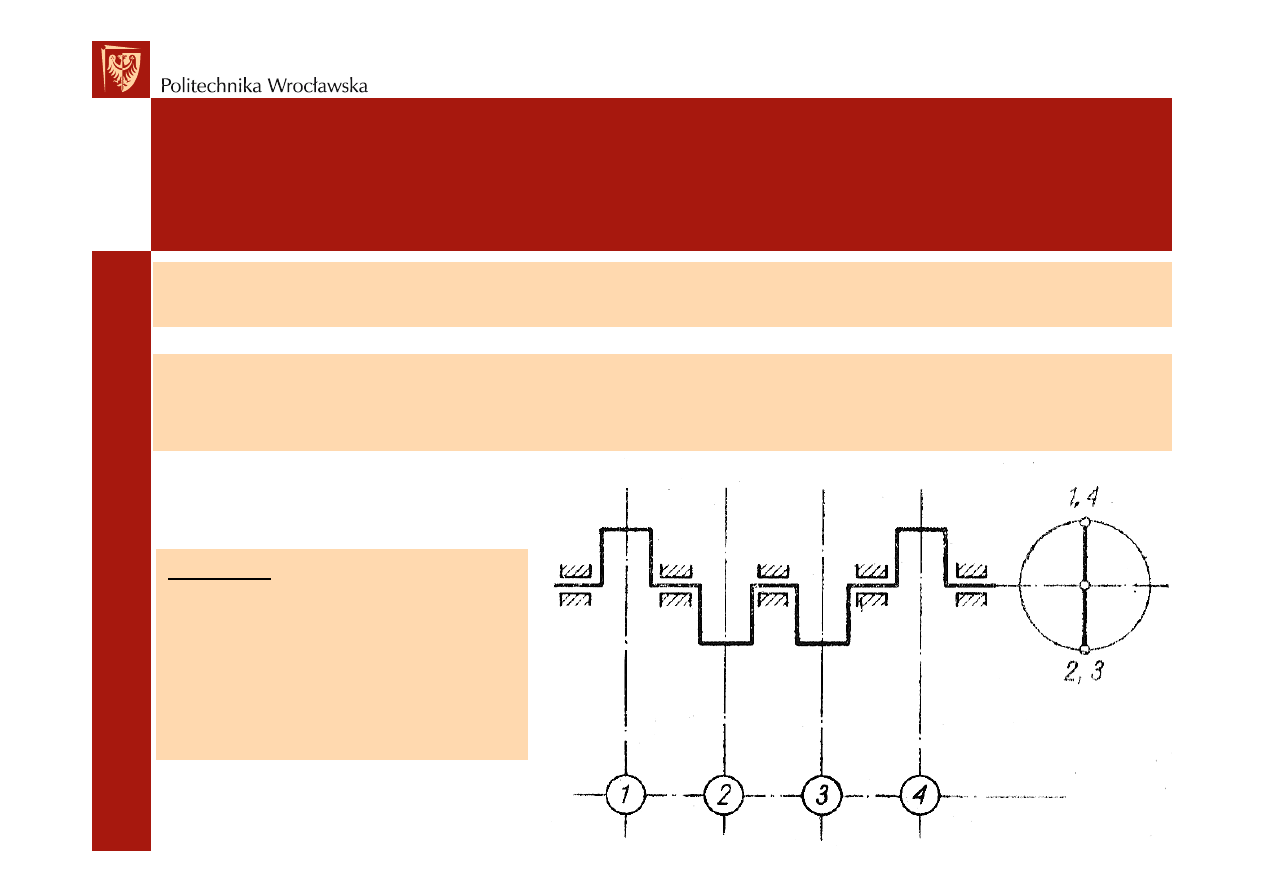
2. W celu zminimalizowania lokalnych obci

ąż

e

ń

wału korbowego i kadłuba silnika,

ka

ż

de dwa s

ą

siednie według kolejno

ś

ci pracy cylindry powinny znajdowa

ć

si

ę

mo

ż

liwie daleko od siebie.

Przykład:

silnik rz

ę

dowy

cztery cylindry
k

ą

t fazowy

γ

= 180°

mo

ż

liwa kolejno

ść

zapłonu:

1-3-4-2 lub 1-2-4-3

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

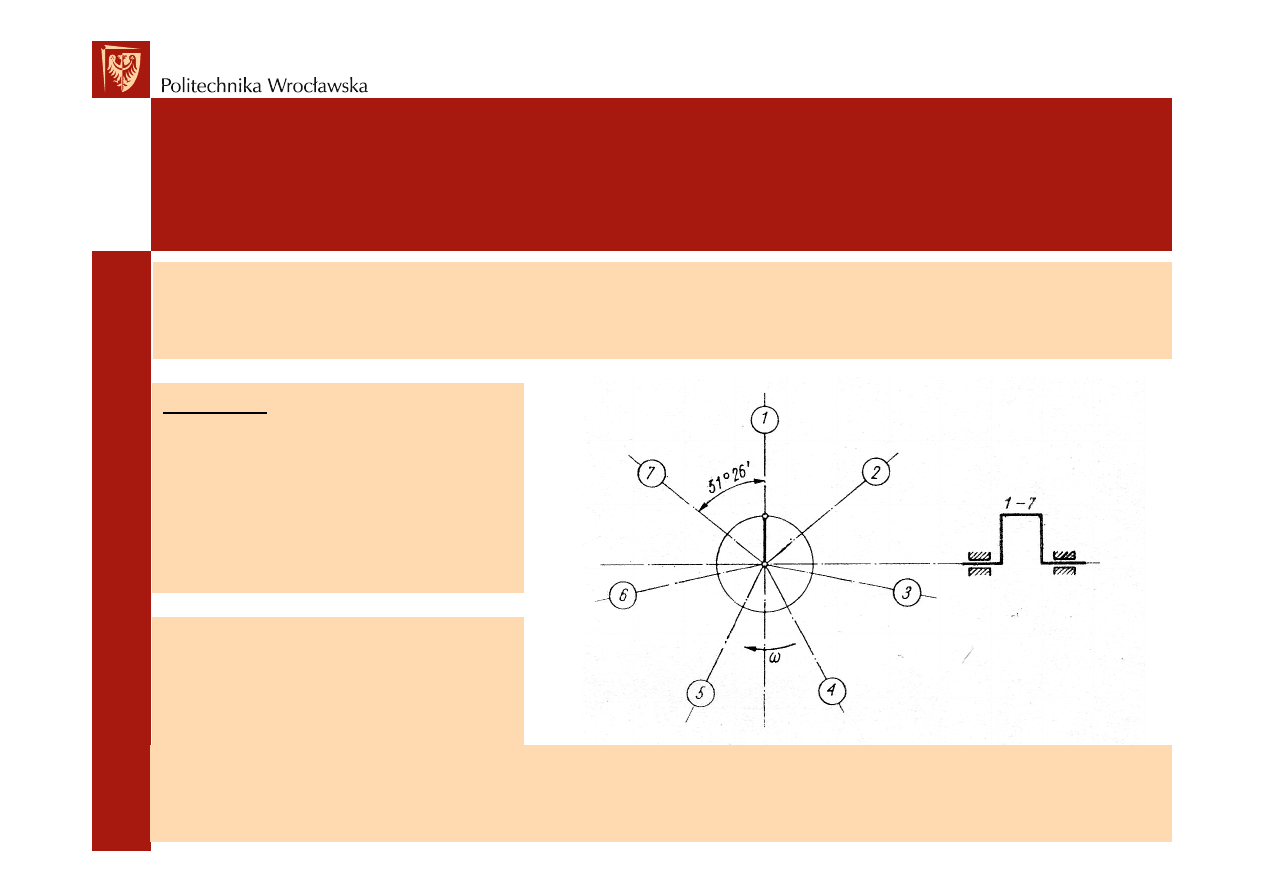
W przypadku silnika gwiazdowego (zwykle i = 5, 7 lub 9), najmniejsze
nierównomierno

ś

ci obci

ąż

enia wału korbowego wyst

ę

puj

ą

przy zastosowaniu

kolejno

ś

ci zapłonu co drugi cylinder w kierunku obrotów wału korbowego.

Przykład:

silnik gwiazdowy
siedem cylindrów
k

ą

t fazowy

γ

= 102°52’

mo

ż

liwa kolejno

ść

zapłonu:

1-3-5-7-2-4-6

Wykorbienie wału korbowego
silnika ze zło

ż

onym układem

korbowo-tłokowym przejmuje
od ka

ż

dego korbowodu sił

ę

styczn

ą

T (wywołuj

ą

c

ą

moment obrotowy) i sił

ę

normaln

ą

Z, przy czym zmienno

ś

ci

tych sił w praktyce nie zale

żą

od cylindra, którego zło

ż

enie tłok-korbowód je

przekazuje.

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

Sumuj

ą

c siły T lub Z od poszczególnych korbowodów, działaj

ą

ce jednocze

ś

nie na

wykorbienie wału, nale

ż

y uwzgl

ę

dni

ć

ich przesuni

ę

cia w fazie o k

ą

ty

α

f

obrotu

wykorbienia wzgl

ę

dem osi cylindra pierwszego (w którym tłok poł

ą

czony jest z

korbowodem głównym).

Je

ż

eli k

ą

t obrotu wału wzgl

ę

dem osi dowolnego cylindra k wynosi

α

k

, to w

odniesieniu do osi cylindra pierwszego wynosi on:

n – liczba porz

ą

dkowa rozpatrywanego cylindra wg kolejno

ś

ci pracy

i – liczba cylindrów w układzie jednej gwiazdy.

(

)

1

720

1

f

k

n

i

α

α

=

+

−

OBCIĄśENIA W UKŁADZIE KORBOWO-TŁOKOWYM

Rozkład obciążeń w układzie korbowym

Ł

ą

cznie z wypadkowym obci

ąż

eniem normalnym korby

Z

ΣΣΣΣ

działa niezmienna siła masowa F

o

powodowana

bezwładno

ś

ci

ą

wszystkich mas układu znajduj

ą

cych si

ę

w ruchu obrotowym.

(

)

2

2

o

W

T

Z

F

Σ

Σ

=

+

+

Wypadkowe obci

ąż

enie wykorbienia W okre

ś

la

zale

ż

no

ść

:

Kierunek siły W okre

ś

la k

ą

t

Θ

Θ

Θ

Θ

mi

ę

dzy płaszczyzn

ą

wykorbienia a wektorem tej siły, przy czym:

o

T

tg

Z

F

Σ

Σ

Θ =

+