Ćwiczenie 10

SPRAWDZANIE PRAWA HOOKE'A;

WYZNACZANIE MODUŁU YOUNGA

Cel ćwiczenia: Sprawdzenie prawa Hooke’a i wyznaczenie modułu Younga

przez pomiar wydłużenia ciała.

Zagadnienia: siły międzycząsteczkowe w ciałach stałych, sprężystość, ro-

dzaje odkształceń, prawo Hooke’a, moduły sprężystości.

10.1. Wprowadzenie

10.1.1. Pojęcie sprężystości, siły międzycząsteczkowe

Rozważając w mechanice newtonowskiej ruchy lub stany równowagi ciał
posługujemy się na ogół pojęciem punktu materialnego lub ciała doskonale
sztywnego. Są to modele matematyczne mogące stanowić w określonych
granicach dopuszczalne przybliżenie ciał rzeczywistych. W przyrodzie bo-
wiem nie ma ani punktów materialnych (gdyż każde ciało ma różną od zera
objętość), ani ciał doskonale sztywnych (gdyż każde ciało, nawet najtward-
sze, jak np. diament, ulega odkształceniom zmieniającym jego objętość lub
kształt, i to już nawet pod wpływem niewielkich sił). Odkształcenia mogą
być u jednych ciał niewielkie (na ogół u ciał stałych), u innych, jak np. cie-
czy lub gazów przy takich samych siłach znaczne.
Ciało nazywamy sprężystym, jeżeli odkształcenia, wywołane działający-
mi na nie siłami, znikają zupełnie po usunięciu tych sił.
Istotę sprężystości można zrozumieć rozważając, chociażby w przy-
bliżeniu, strukturę wewnętrzną ciała stałego. Każde ciało jest zbudowane -

1

jak wiadomo - z atomów lub cząsteczek (w przypadku związków chemicz-
nych), pomiędzy którymi działają siły nazywane międzycząsteczkowymi.
Siły te są (w porównaniu np. z gazami) na skutek małych odległości mię-
dzycząsteczkowych na tyle duże, że cząsteczki (atomy) są - dzięki temu - w
danej temperaturze uporządkowane, tworząc (w różnych ciałach na różne
sposoby) regularną strukturę przestrzenną nazywaną siecią krystaliczną.
Kazda cząsteczka (nazywana z tego punktu widzenia węzłem sieciowym,
a ciało - kryształem) ma swoje położenie równowagi trwałej, wokół którego
wykonuje niewielkie, chaotyczne, zależne od temperatury drgania.
Podkreślić przy tym należy, że powstanie równowagi trwałej - i tym sa-
mym sieci krystalicznej - wynika z faktu, że pomiędzy każdymi dwiema
cząsteczkami występują dwojakiego rodzaju siły: przyciągania oraz odpy-

chania. Jedne i drugie zależą od
odległości między-
cząsteczkowej - rosną, gdy ta
maleje, lecz niejednakowo. Siły
odpychania rosną od pewnej
odległości między cząsteczkami
znacznie bardziej wraz ze zbli-
żaniem się ich do siebie niż siły
przyciągania. Dzięki temu przy
pewnej odległości pomiędzy

cząsteczkami siły przyciągania i
odpychania znoszą się. Przy

odległościach

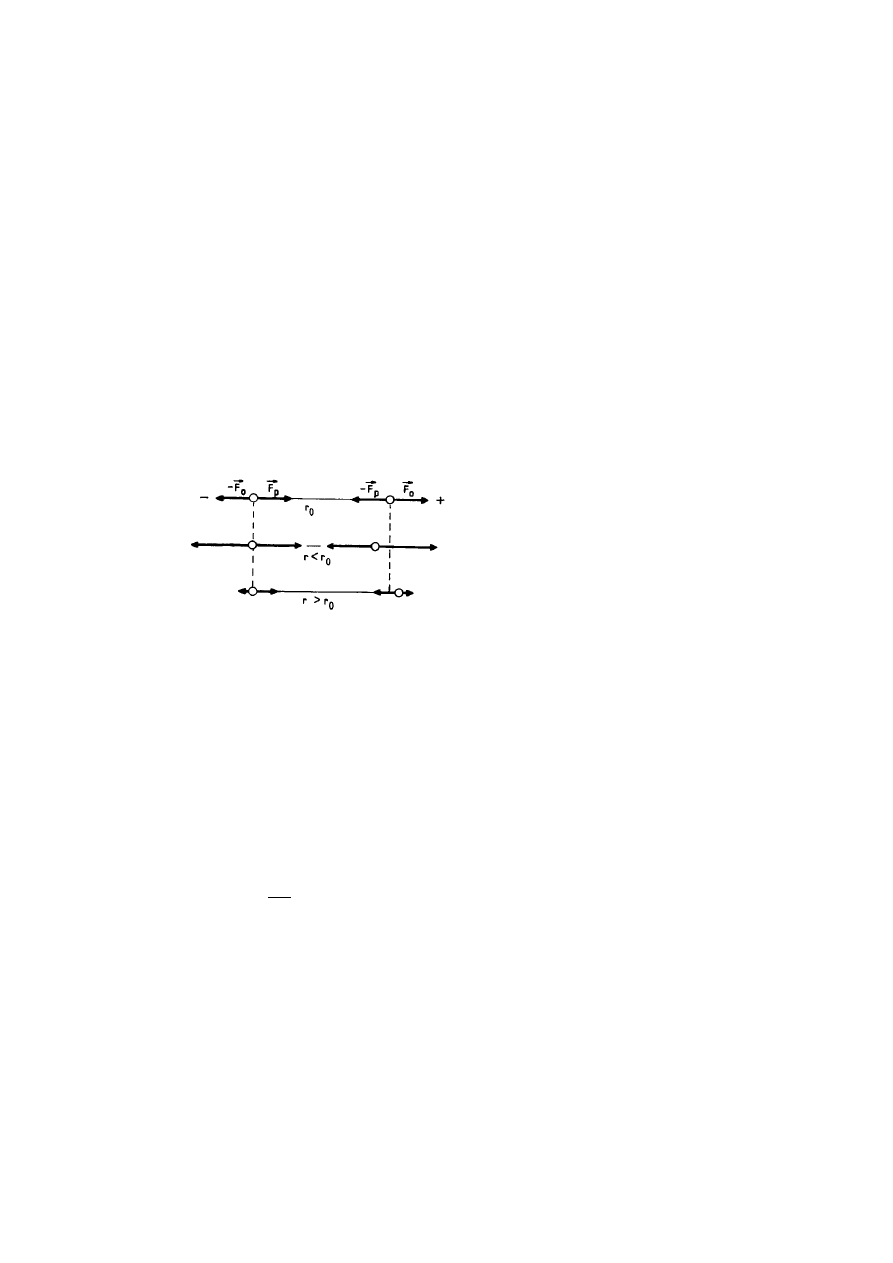
przeważają siły przyciągania, przy r

- odpychania,

co ilustruje rys. 10.1.

r

0

r r

<

0

r

>

0

Rys. 10.1.
Siły międzycząsteczkowe:

- przycią-gania,

- odpychania, - odległość równowagi

(proporcje na rysunku nie odpowiadają rzeczy-
wistości)

F

p

F

0

r

0

Siłę przyciągania

, odpychania

oraz ich wypadkową

F działającą

na jedną cząsteczkę przedstawiają w przybliżeniu zależności:

F

p

F

0

m

p

r

a

F

−

=

,

(10.1)

2

n

r

b

F

=

0

,

(10.2)

m

n

r

a

r

b

F

−

=

,

(10.3)

Stałe

a i b zależą od budowy znajdującej się w węźle sieci cząsteczki

oraz - tym samym - od rodzaju sił wiązania. Wykładnik dla sił odpychania
jest z reguły rzędu 9 (

), a dla sił przyciągania wynosi w zależności od

typu wiązania od 2 do 7 (

m

= 9

7

2

÷

=

n

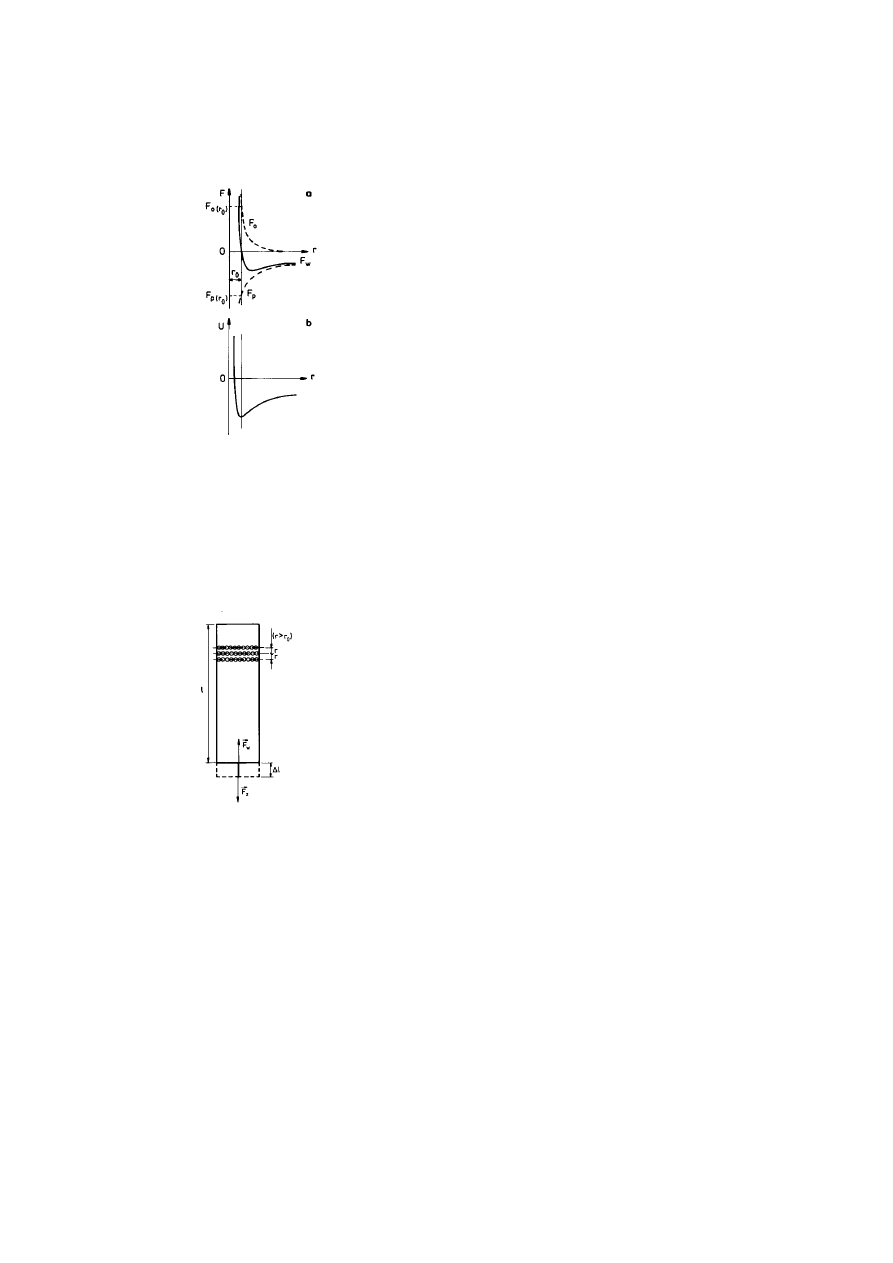
). Rysunek 10.2 przedstawia wykresy

wzorów (10.1) - (10.3).
Każda cząsteczka w krysztale znajduje się w polu sił wytworzonym
przez teoretycznie wszystkie inne otaczające ją cząsteczki. Praktycznie jed-
nak wpływają na nią, z uwagi na wysokie potęgi

m i n we wzorach (10.1)

i (10.2), tylko te najbliżej położone (

sfera oddziaływania, rys. 10.3). Czą-

steczka posiada w tym polu określoną energię potencjalną oraz - wykonując
chaotyczne drgania - energię kinetyczną (której średnia wartość jest wprost
proporcjonalna do temperatury absolutnej

T). Na rysunku 10.2b przedsta-

wiono wykres energii potencjalnej sił wzajemnego oddziaływania dwóch
cząsteczek (linią przerywaną wrysowano siłę wypadkową według wzoru
(10.3)).
Wyrażenie na energię potencjalną

U jako funkcję odległości r otrzymuje

się z (10.3) wychodząc z ogólnej zależności pomiędzy energią potencjalną
i siłą w polu sił

dr

dU

F

−

=

,

(

)

( )

(

)

(

)

1

1

1

1

−

−

−

−

−

=

m

n

r

a

m

r

b

n

U

.

(10.4)

Z wykresu 10.2b widać, że cząsteczka znajdująca się w odległości od

sąsiedniej (dla w kryształu oznacza to: w węźle sieci) posiada minimum
energii potencjalnej, co - jak wiadomo - jest wyznacznikiem stanu równo-

r

0

3

wagi

trwałej. W innych położeniach jej energia potencjalna jest - kosztem

kinetycznej - od tego minimum większa.

Rys. 10.2.

a - siły międzycząsteczkowe, b - energia potencjalna jako funkcje
odległości cząsteczek (linia przerywana na rys. b - siła wypadkowa
z rys. a)

Rozróżniamy, nie wnikając w subtelności, cztery rodzaje wiązań atomów
lub cząsteczek w ciałach stałych (czyli kryształach):

Rys. 10.3.
Siły międzycząsteczkowe są siłami krótkozasięgowymi. Sfera
oddzia-ływania (o promieniu d) obejmuje tylko najbliższych
sąsiadów

1.

Wiązanie jonowe (albo heteropolarne lub walencyjne), które powstaje na

skutek przyciągania się rozmieszczonych w krysz-tale na przemian różno-
imiennych jonów, jak np. w kryształach

NaCl lub KCl. Jony powstają dlate-

4

go, że przy dostatecznym zbliżeniu i dostatecznie niskiej temperaturze jedne
atomy tracą a inne przyjmują elektrony (

,

Na

+

Cl

−

). O samym tym fakcie

jak i kierunku przejścia elektronu decyduje zmniejszenie się enrgii całkowi-
tej układu ciał jakim jest zbiorowisko atomów (które zatem w stałym stanie
skupienia znajdują się w równowadze bardziej trwałej niż w ciekłym czy
tym bardziej gazowym).
2.

Wiązanie atomowe (albo homopolarne lub kowalentne), które jest wyni-

kiem tego, że dwa sąsiadujące ze sobą atomy posiadają dwa (w niektórych
przypadkach jeden)

wspólne elektrony przebywające najczęściej pomiędzy

nimi (na prostej łączącej jądra). Jest tak np. w dia-mencie i graficie (dwóch
odmianach krystalicznych węgla), krzemie, germanie, siarczku węgla i in. w
tym w bardzo wielu kryształach organicz-nych, w których o wiązaniu kowa-
lentnym decydują właśnie atomy węgla. Niekiedy mówi się o

wspólnej po-

włoce elektronowej (składającej się z dwóch elektronów) otaczającej takie
atomy.
3.

Wiązanie metaliczne, które wynika z tego, że w krysztale istnieje grupa

elektronów wspólna dla wszystkich atomów (a nie tylko dla dwóch, jak
w przypadku wiązania atomowego - po dwa na każdą parę sąsiadujących ze
sobą atomów). Nazywamy je

elektronami swobodnymi, gdyż jako nie zwią-

zane z żadnym konkretnym węzłem sieci mogą się one w obrębie całego
kryształu swobodnie przemieszczać. Ten rodzaj wiązania decyduje
o istnieniu i właściwościach (m.in. elektrycznych) metali.
4.

Wiązanie Van der Waalsa (albo cząsteczkowe). W kryształach o tym ty-

pie wiązania w węzłach sieci znajdują się obojętne cząsteczki lub atomy.
Siły pomiędzy nimi powstają na skutek oddziaływania ich wewnętrznych
pól elektrycznych (co prowadzi np. do wzajemnego indukowania się dipoli
elektrycznych) oraz na skutek oddziaływania drgających ładunków elek-
trycznych. Do tej klasy wiązań należą np. kryształy bromu (

), jodu

(

), dwutlenku węgla (

), wodoru (

). Siły Van der Waalsa stano-

wią wiązanie najsłabsze, zarazem jest to jednak wiązanie uniwersalne, wy-

Br

2

J

2

CO

2

H

2

5

stępujące we wszystkich kryształach niezależnie od innych typów wiązań.
W przypadku krystalicznego wodoru są one jedynymi siłami wiążącymi
atomy.
Praktycznie nie ma, poza wodorem, kryształu o czystym, jednym typie
wiązania. W każdym przypadku można mówić o dominacji jednego typu
nad innymi. Poza tym rzadko mamy do czynienia z ciałami jako jednolitymi
kryształami, czyli

monokryształami. Ciała krystaliczne są przeważnie poli-

kryształami, czyli chaotycznymi zlepkami maleńkich, mikroskopowej wiel-
kości kryształków, tzw.

krystalitów albo ziaren. W szczególności odnosi się

to metali. Struktura polikrystaliczna powstaje dlatego, że proces krystaliza-
cji rozpoczyna się w temperaturze krzepnięcia w bardzo wielu miejscach
równocześnie, na licznych

zarodkach krystalizacji, którymi są zazwyczaj

znajdujące się w cieczy zanieczyszczenia. Dlatego uzyskanie monokryształu
wymaga często licznych, niekiedy trudnych zabiegów, a przede wszystkim

nadzwyczaj czystej cieczy wyjściowej.
Siły działające na ciało wywołują, jak
wspomniano, ich odkształcenia. Prześledźmy
powstawanie wydłużenia pręta pod wpływem
sił rozciągających, działających wzdłuż jego
osi, np. w przypadku pręta lub drutu przymo-
cowanego np. do sufitu i obciążonego jakimś
ciężarkiem (rys. 10.4). Niech warstwy cząste-

czek (

płaszczyzny sieciowe) będą ułożone prostopadle do osi pręta. Jedna

warstwa znajduje się od drugiej, przed przyłożeniem siły zewnętrznej

, w

od-ległości równowagi . Siła

, rozciągając każdą leżącą wzdluż osi

parę cząsteczek równowagę tę zakłóca. Wzrost odległości (

r

) oznacza

przyrost długości pręta (

F

z

r

0

l

F

z

r

r

>

0

)

(

0

r

−

Σ

=

∆

F

w

) i spowoduje zgodnie z tym, co wy-

żej powiedziano - większy spadek sił odpychania niż przyciągania, a więc
pojawi się przewaga sił przyciągania się każdej pary, co jako wypadkową da
pewną siłę wewnętrzną

, przeciwdziałającą sile zewnętrznej. Przyrasta-

Rys. 10.4. Rozciąganie

6

nie długości ustanie w tym momencie (przy takiej wartości

∆l ), w którym

siła

zrównoważy siłę

. Będzie to oznaczało nowy stan równowagi

trwałej dla zwiększonej odległości cząsteczek.

F

w

0

→

F

z

∆

p

Jeżeli teraz usuniemy siłę zewnętrzną, to pod wpływem nadal istniejącej
siły wewnętrznej cząsteczki będą się z powrotem do siebie zbliżać, a siła ta
będzie zanikać. Jeżeli nastąpi powrót do poprzednich odległości

(tzn.

), to oznacza to, że odkształcenie było

sprężyste. Jeżeli natomiast

odkształcenie nie zniknie całkowicie, to pozostałą jego część

nazywa-

my odkształceniem

trwałym albo plastycznym. Mówimy w takim przypad-

ku, że przy obciążeniu została przekroczona

granica sprężystości. Może

powstać też taka sytuacja (przy dostatecznie dużym obciążeniu), że przy
żadnej wartości

r

0

∆l

l′

∆l nie powstanie siła wewnętrzna równoważąca siłę ze-

wnętrzną (przy wzroście odległości wzajemnej cząsteczek maleją, jak
wspomniano, nie tylko siły odpychania lecz również przyciągania). Pręt
ulega wtedy zerwaniu i mówimy, że wywołane przez siłę zewnętrzną naprę-
żenie przekroczyło

granicę wytrzymałości.

W

rzeczywistości proces odkształcania pręta nie przebiega tak prosto, jak

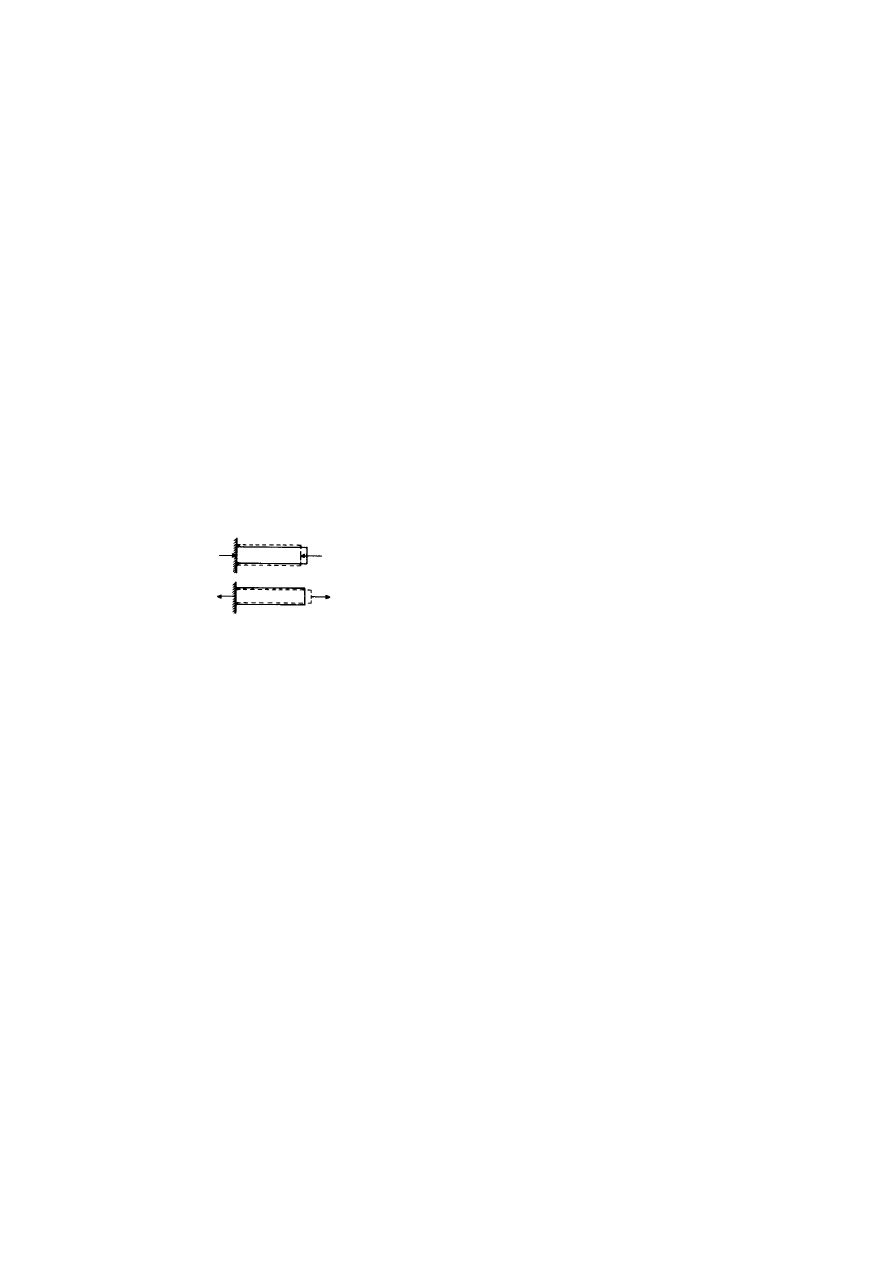
to przedstawiono. Trzeba też dodać, że każdej zmianie długości (rozmiarów
równoległych do kierunku działania sił), towarzyszy zmiana średnicy (wy-
miarów poprzecznych) - rys. 10.5.

10.1.2. Naprężenia, odkształcenia

Naprężeniem nazywamy wektor o wartości równej stosunkowi wartości
siły do powierzchni, na którą ona działa, o kierunku i zwrocie zgodnym
z kierunkiem i zwrotem wektora siły:

S

=

F

,

(10.5)

Jeżeli przez

F rozumiemy siłę wewnętrzną

, to naprężenie nazywamy

wewnętrznym

. Dla siły zewnętrznej mówimy odpowiednio

F

w

p

w

7

o wywieranym na ciało naprężeniu zewnętrznym

. Podobnie jak siłę

można też naprężenie rozłożyć na składową normalną (

) i styczną (

).

p

z

p

n

p

t

V

k

p

<

Naprężenie normalne, nazywane też w przypadku siły ściskającej ciało
ciśnieniem, a w przypadku siły rozciągającej ciągnieniem, powoduje na
ogół zmianę objętości ciała, naprężenie styczne natomiast zmianę postaci.
Jednostki:

]

[

]

[

]

[

S

F

p

=

,

Pa

m

N

]

2

SI

=

=

p

[

Jednostką naprężenia jest takie naprężenie, jakie wywołuje jednostkowa
siła działając normalnie (prostopadle) na jednostkową powierzchnię. Jed-
nostką naprężenia w układzie

SI, o nazwie paskal (Pa), jest takie napręże-

nie, jakie wywołuje siła jednego niutona działając prostopadle na po-
wierzchnię jednego metra kwadratowego.
Wszelkie,

różnorodne odkształcenia, jakim ulegają ciała pod wpływem

działających na nie sił, można sprowadzić do trzech głównych rodzajów
odkształceń:

jednostronnego (jednokierunkowego) ściskania lub rozciąga-

nia,

wszechstronnego ściskania lub rozciągania oraz ścinania.

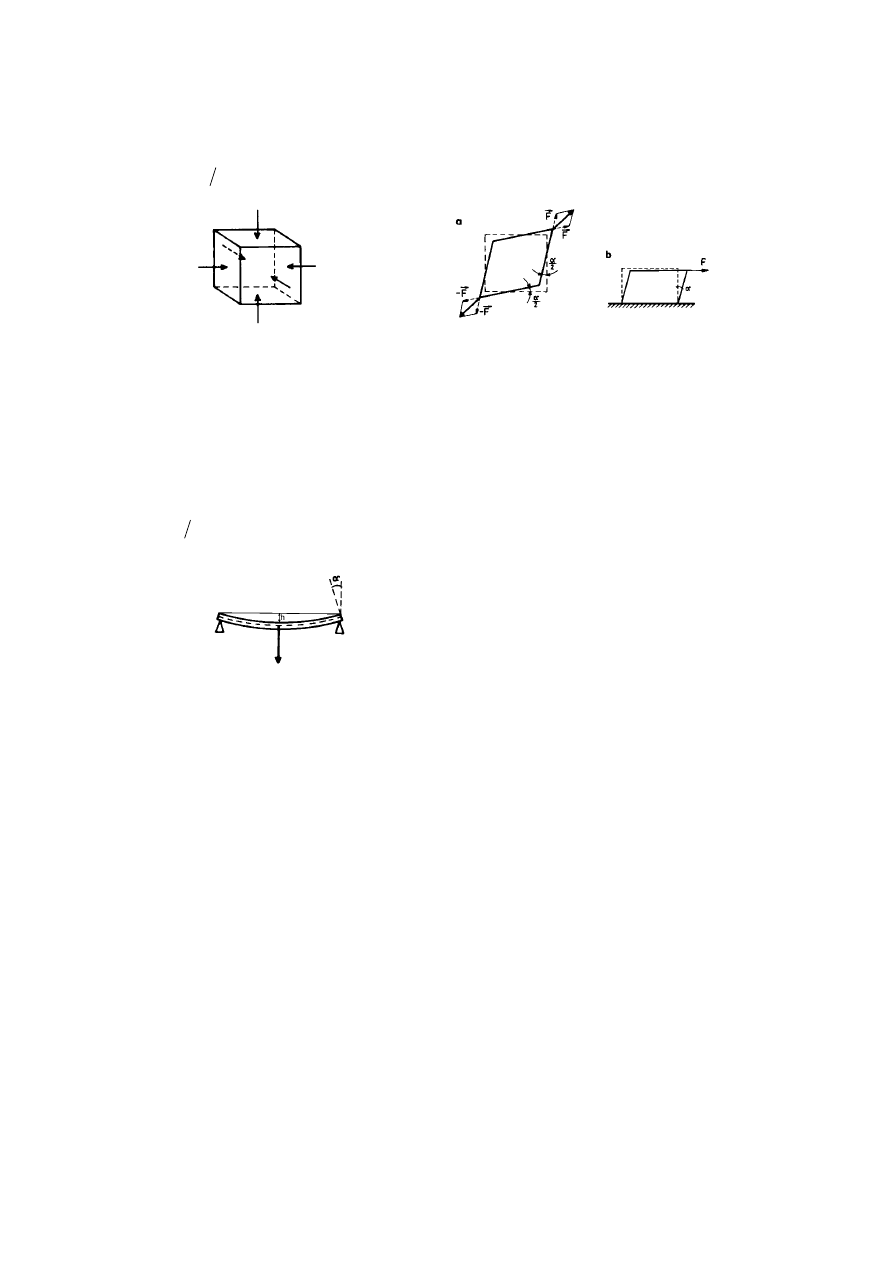
1. Odkształcenie jednostronne występuje wtedy, gdy siły działają na dwie
przeciwległe ściany ciała, prostopadle do nich (gdy siły leżą na jednej pro-
stej, tak że suma ich momentów względem dowolnego punktu ciała jest w
każdej chwili równa zeru) - rysunek 10.5. Skutkiem działania sił jest w ta-
kim przypadku przyrost długości

∆l , który nazywamy odkształceniem bez-

względnym. Natomiast stosunek przyrostu długości do długości początkowej

∆l l

∆

nazywamy

odkształceniem względnym. Podczas rozciągania jest

l >0, podczas ściskania jest

∆l <0.

2. Odkształcenie wszechstronne występuje wtedy, gdy na każdy element
powierzchni ciała działa siła do niego prostopadła, rysunek 10.6. W tym
przypadku za miarę odkształcenia bezwzględnego umówiono się uważać
przyrost objętości wzięty ze znakiem minus,

−∆V (czyli ubytek objętości).

Odkształcenie ma dzięki temu przy ściskaniu (

V

) wartość dodatnią,

8

0

)

(

>

−

−

=

∆

−

p

k

V

V

V

, przeciwnie niż przy odkształceniu jednostronnym.

Odkształceniem względnym nazywamy w tym przypadku stosunek

V

V

∆

−

.

α

l

Rys. 10.5. Odkształcenie jednostronne

Rys. 10.6. Odkształcenie wszechstronne

3.

Ścinanie jest odkształceniem, które występuje wtedy, gdy działające na

ciało siły są styczne do jego powierzchni, rysunki 10.7. Miarą odkształcenia
bezwzględnego jest w tym przypadku kąt skręcenia ścianek

α (miarą od-

kształcenia względnego byłby - dla

α wyrażanego w radianach - stosunek

).

Rys. 10.7. Ścinanie

Zginanie można sprowadzić, zgodnie z tym co wyżej stwierdzono, do rów-
noczesnego ściskania górnej i rozciągania dolnej (przeciwległych) po-
wierzchni ciała, rysunek 10.8. W ciele znajduje się wtedy strefa neutralna
(linia kreskowana na rysunku), która nie podlega ani ściskaniu ani rozciąga-
niu. Miarą odkształcenia jest strałka ugięcia

h.

9

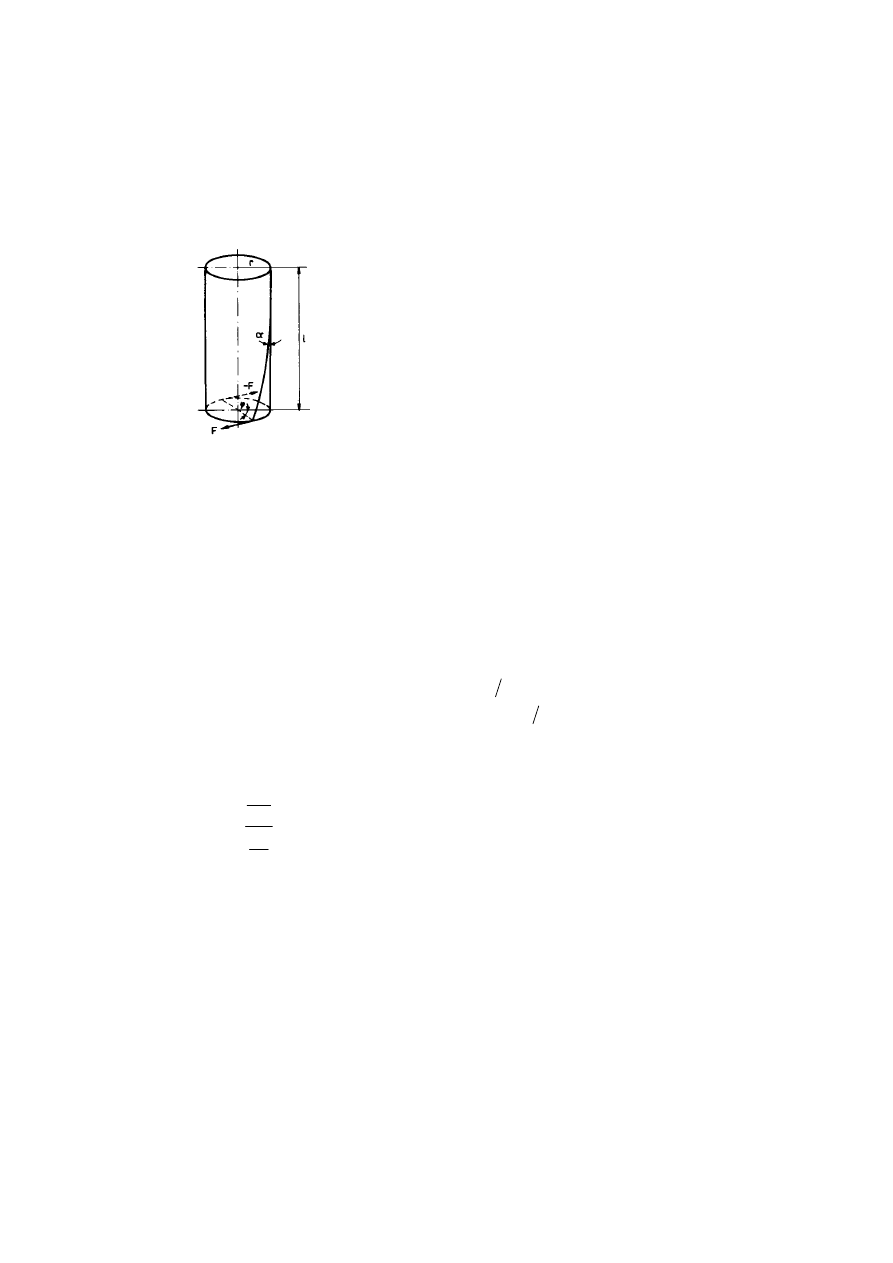
Skręcenie pręta lub drutu o jakiś kąt

φ

, spowodowane momentem siły

względem jego osi polega na ścinaniu o kąt

α

każdego elementu objętości

w przekroju prostopad-łym do osi względem położenia początko-wego

(rys. 10.9).
Rozciąganie sprężyny walcowej, która
pozornie zachowuje się jak pręt o bardzo
dużych wydłużeniach

∆l , polega na ścina-

niu, ponieważ podczas zbliżania lub odda-
lania zwoju od zwoju sprężyny następuje
skręcanie drutu, z którego jest ona wyko-
nana. Natomiast skręcania płaskiej spręży-
ny ślimakowej, (np. takiej, jaka znajduje
się w zegarku mechanicznym lub zabaw-
kach napędzanych mechanicznie), która
pozornie zachowuje się jak tarcza ulegają-

ca skręceniom o duże kąty, polega na zginaniu stalowej taśmy, z której taka
sprężyna jest wykonana, a więc ostatecznie sprowadza się do odkształcenia
jednostronnego.

Rys. 10.9. Skręcanie

Podczas

jednostronnego

ściskania lub rozciągania następuje - jak wspo-

mniano - nie tylko zmiana długości, lecz również zmiana średnicy; rozcią-
gany pręt staje się cieńszy. Okazuje się, że względna zmiana rozmiarów
poprzecznych do kierunku działania sił (

∆d d

) jest wprost proporcjonalna

do względnej zmiany rozmiarów podłużnych (

∆l l

). Stosunek tych dwóch

wartości, charakterystyczny dla danego materiału nazywamy

współczynni-

kiem albo liczbą Poissona

µ

:

l

l

d

d

∆

∆

µ

=

.

(10.6)

Wartości liczby Poissona dla większości metali zawierają się w granicach
0,2 - 0,5.

10

10.1.3. Prawo Hooke’a

Prawo

Hooke’a

wyraża zależność pomiędzy naprężeniem a odkształ-

ceniem:
Jeżeli występujące w ciele naprężenia są dostatecznie małe, to wywołane
przez nie odkształcenia względne są do nich wprost proporcjonalne.
Matematycznie

związek powyższy wyrażają różne wzory, zależnie od

rodzaju odkształcenia. Dla wymienionych wyżej głównych rodzajów od-
kształceń ma on odpowiednio następujące postacie

σ

E

l

l

1

=

∆

,

σ

K

V

V

1

=

∆

−

,

τ

α

G

1

=

. (10.7)

Współcznniki proporcjonalności 1/

E, 1/K, 1/G nazywamy współczynnikami

sprężystości, a ich odwrotności - modułami, odpowiednio: E - modułem
Younga, K - modułem ściśliwości, G - modułem sztywności. Są to stałe cha-
rakterystyczne dla danego rodzaju ciał, tzw. stałe materiałowe. Pośród meta-
li największe wartości tych modułów ma stal, najmniejsze - aluminium. W
przybliżeniu wynoszą one:
Fe: E=216,000 MPa ,

K=163,000 MPa ,

G = 79,500 MPa ,

Al: E=71,600 MPa ,

K=74,600 MPa ,

G = 26,500 MPa ,

1 MPa=106Pa - megapaskal.
Pomiędzy modułami oraz liczbą Poissona zachodzą następujące związki

(

)

µ

2

1

3

−

= K

E

,

(

)

µ

+

=

1

2G

E

.

(10.8)

Dla innych odkształceń, np. zginania pręta o przekroju prostokątnym
oraz skręcania pręta o przekroju kołowym wynikają z prawa Hooke’a nastę-
pujące wzory:

bE

a

F

l

h

3

3

4

=

,

G

r

lM

4

2

π

ϕ

=

,

(10.9)

gdzie:

l - długość pręta, h - strzałka ugięcia, a - wysokość pręta (w kierunku

działania siły),

b - szerokość pręta, F - siła działająca na środek pręta pod-

11

partego na końcach (rys. 10.8),

E - moduł Younga,

###

- kąt skręcenia, r -

promień pręta,

M - moment pary sił (rys. 10.9), G - moduł sztywności.

Ponieważ zginanie sprowadza się do równoczesnego ściskania
i rozciągania przeciwległych powierzchni, więc zrozumiałe jest, że we wzo-
rze na strzałkę ugięcia występuje moduł

E, natomiast ponieważ skręcanie

sprowadza się do ścinania, nie dziwi, że we wzorze na kąt skręcenia wystę-
puje moduł

G.

Siła zewnętrzna odkształcająca ciało wykonuje pracę przeciwko siłom
wewnętrznym. Praca ta zostaje w przypadku odkształcenia sprężystego
zgromadzona w ciele jako jego

energia potencjalna sprężystości, natomiast

w przypadku odkszałcenia plastycznego - jako energia cieplna powodująca
wzrost jego temperatury.
Wychodząc z prawa Hooke’a można wykazać, że

energia sprężysta

przypadająca na jednostkę objętości ciała

V

E

p

/

=

ε

, czyli tzw.

gęstość

energii sprężystej jest z odpowiednim do rodzaju odkształcenia modułem
wprost proporcjonalna do kwadratu odkształcenia względnego

2

2

1











 ∆

=

l

l

E

ε

,

2

2

1











 ∆

=

V

V

E

ε

,

2

2

1

α

ε

E

=

. (10.10)

Odkształcenie sprężyste nie następuje natychmiast po przyłożeniu siły, jak-
kolwiek ustala się po czasie zazwyczaj bardzo krótkim. W procesie narasta-
nia odkształcenia można wyodrębnić dwie fazy: bardzo szybkiego powsta-
nia odkształcenia początkowego i wolniejszego dochodzenia do wartości
końcowej, przewidzianej przez prawo Hooke’a. Podobnie jest z zanikaniem
odształcenia po ustaniu działania siły. Zjawisko to nazywamy opóźnieniem
sprężystym.
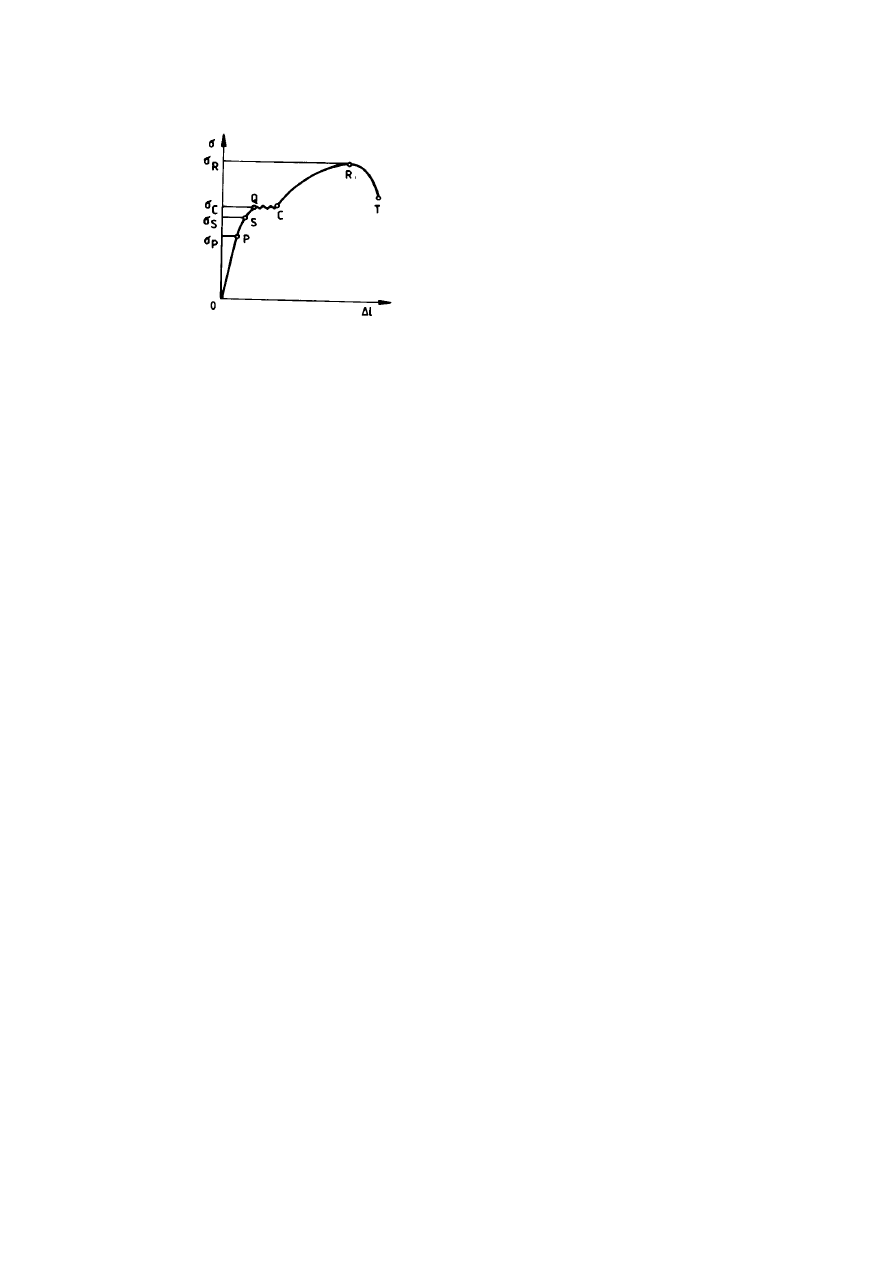
Na rysunku 10.10 przedstawiono przykładowo pełny wykres zależności
naprężenia wewnętrznego w ciele od wymuszonego na nim wydłużenia.

12

13

Wykres jest do pewnego punktu P,
dla małych odkształceń i naprężeń,
prostoliniowy, co odpowiada pra-
wu Hooke’a. Odpowiadające temu
punktowi naprężenie

σ

P

nazywa-

my granicą proporcjonalności.
Granica proporcjonalności nie jest
jednoznacznie określona, ponie-
waż nie da się jednoznacznie okre-
ślić położenia punktu P jako końca

odcinka prostoliniowego. Można to zrobić jedynie z określonym przybliże-
niem, na jakie pozwalają warunki pomiaru. Nieco powyżej, na ogół blisko,
znajduje się punkt S i odpowiadające mu naprężenie

σ

s

- granica spręży-

stości. Dalszy przebieg krzywej jest dla różnych materiałów bardzo różny.
Przedział Q - C, który charakteryzuje się dużymi odkształceniami przy nie-
znacznych zmianach naprężenia, nazywany jest obszarem ciągliwości lub
płynności. Wyraźnie występuje on np. w stali miękkiej. Obszar ten ma duże
znaczenie techniczne, dzięki niemu bowiem istnieje możliwość obróbki
metali przez kucie, walcowanie, przeciąganie i in. Największe naprężenie

σ

R

, jakie może powstać w ciele, nazywamy granicą wytrzymałości. Na

przekraczaniu tej granicy polega obróbka skrawaniem, np. toczenie, frezo-
wanie, wiercenie. Niektóre ciała, np. żeliwo, praktycznie nie mają obszaru
ciągliwości; granice proporcjonalności, sprężystości i wytrzymałości niemal
się pokrywają. Nazywamy je ciałami kruchymi.

Rys. 10.10. Wykres naprężeń

10.2. Stanowisko pomiarowe

Sprawdzenie prawa Hooke’a polega na wykonaniu kilku pomiarów wy-
dłużenia

l stalowego drutu pod wpływem znanego obciążenia

i sporządzenia wykresu

###

Q mg

=

( )

∆l

f Q

=

oraz zbadanie czy (ew. do jakiego punk-

tu) jest on prostoliniowy. Dla ostatniego punktu (

Q;

l), który można

uznać za leżący jeszcze na odcinku prostoliniowym wykresu należy obli-
czyć moduł Younga. W tym celu należy wykonać dodatkowo pomiary dłu-
gości drutu

l oraz jego średnicy d.

###

Z (10.7), (10.5) oraz wzoru na po-
wierzchnię koła

otrzymuje się

(przy

Q

4

/

2

d

S

π

=

mg

=

) wzór na moduł Younga

l

d

mgl

E

∆

=

2

4

π

.

(10.11)

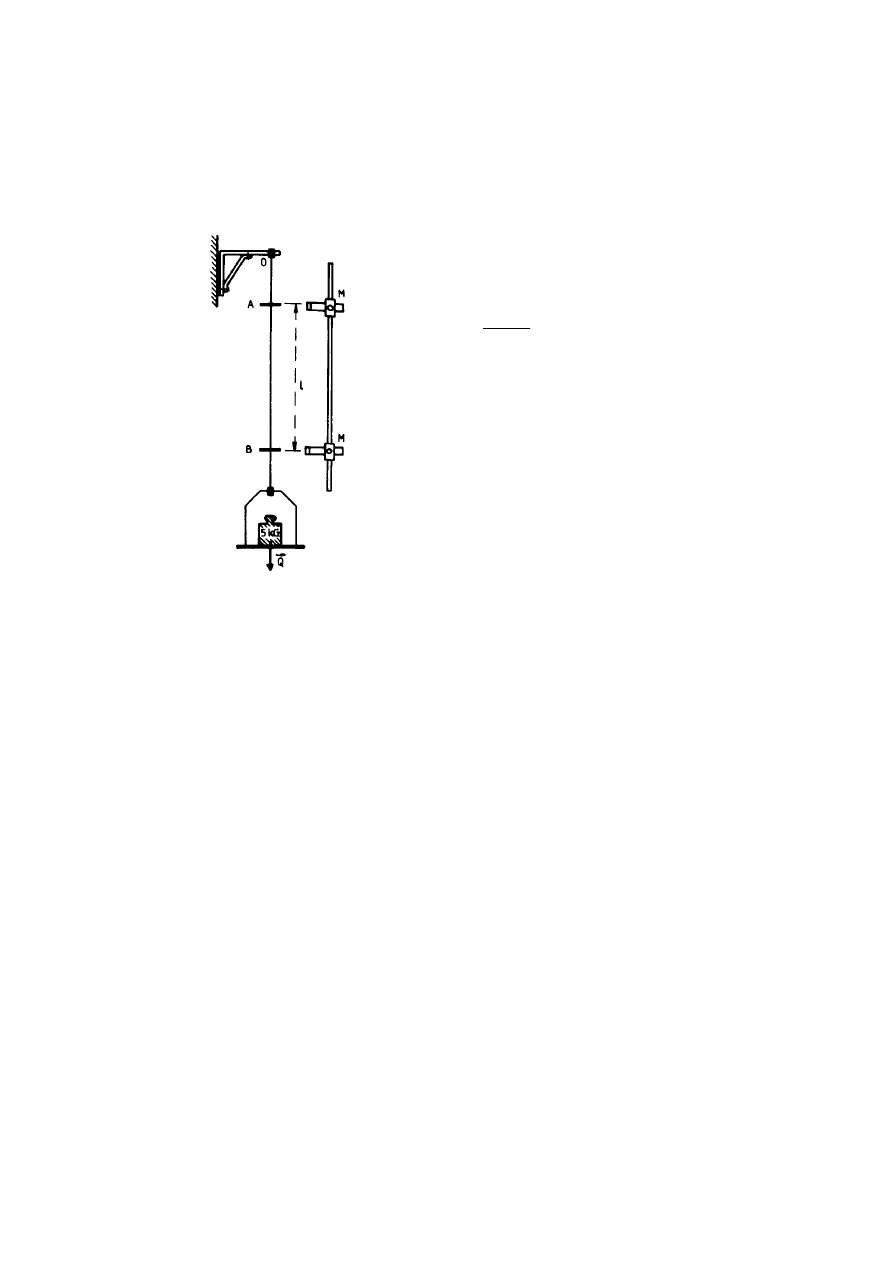
Na rysunku 10.11 przedstawiono sche-
matycznie układ pomiarowy. Górny koniec
drutu jest zaczepiony do przymocowanego
do ściany wysięgnika, na dolnym jego koń-
cu znajduje się szalka na odważniki.
Do drutu przymocowane są dwa wskaźniki
A i B ustalające długość badanego odcin-
ka

l. Wydłużenie

∆l mierzymy jako różnicę

wydłużeń odcinków

OB i OA.

Równolegle do drutu jest przytwierdzony
do ściany pręt wzdłuż którego można prze-

suwać mikroskop

M służący do pomiarów przesunięć wskaźników.

W

okularze mikroskopu znajduje się szklana płytka ,,ogniskowa”

z naniesioną skalą służącą do określania rozmiarów obrazów oraz ich prze-
sunięć. Przesunięcie wskaźnika

A równa się liczbie a działek skali (lub b w

przypadku wskaźnika

B), o jaką przesunie się jego obraz, pomnożonej przez

powiększenie

w mikroskopu. Zatem

Rys. 10.11. Układ pomiarowy

(

)

∆l w b a

=

−

.

(10.12)

Jeżeli powiększenie mikroskopu nie jest znane, to należy je zmierzyć: jako
stosunek np. grubości

q wskaźnika (zmierzonej ostrożnie przy pomocy śru-

14

by mikrometrycznej) do grubości

q’ jego obrazu w mikroskopie, wyrażonej

w liczbie działek skali na płytce ogniskowej mikroskopu,

w=q/q’.

Uwagi: W trakcie wykonywania obserwacji należy zwracać baczną uwagę
na ostrość obrazu w mikroskopie, ponieważ wpływa ona na dokładność po-
miaru parametrów

a, b, q i q’. Ostrość reguluje się przy pomocy pokrętła

przesuwającego mikroskop wzdłuż jego osi. Obraz w mikroskopie jest od-
wrócony, w związku z czym przesunięciu wskaźnika w dół odpowiada prze-
sunięcie się jego obrazu w górę. Należy też zwracać uwagę na to, aby skala
na płytce ogniskowej była pionowa, tj. równoległa do drutu i prostopadła
tym samym do obrazów wskaźników.
Sporządzić odpowiednie tabelki i do nich wpisywać wszystkie pomiary.

10.3. Zadania do wykonania

A) Zadania pomiarowe
1. Wykonać pomiar powiększenia mikroskopu obserwacyjnego - jeżeli jego

wartość nie jest podana w instrukcji wykonawczej.

2. Wykonać dla znajdujących się na stanowisku odważników serię pomia-

rów

( )

Q

f

l

=

∆

3. Wykonać pomiary długości drutu

l pomiędzy wskaźnikami A i B.

4. Wykonać na całym odcinku

l dziesięć pomiarów średnicy drutu d

(w różnych kierunkach prostopadłych do jego osi). Obliczyć i również wpi-
sać do tabeli ich średnią arytmetyczną

d

sr

.

B) Opracowanie wyników

1. Sporządzić wykres

( )

∆l

f Q

=

. przerysować na papier milimetrowy i

załączyć do sprawozdania.

2. Określić zakres naprężeń, dla których spełnionejest prawo Hooke’a.
3. Dla zakresu w którym spełnione jest prawo Hooke’a wyznaczyć me-

todą regresji liniowej moduł Younga.

15