Przykładowe zadania z linii

długiej

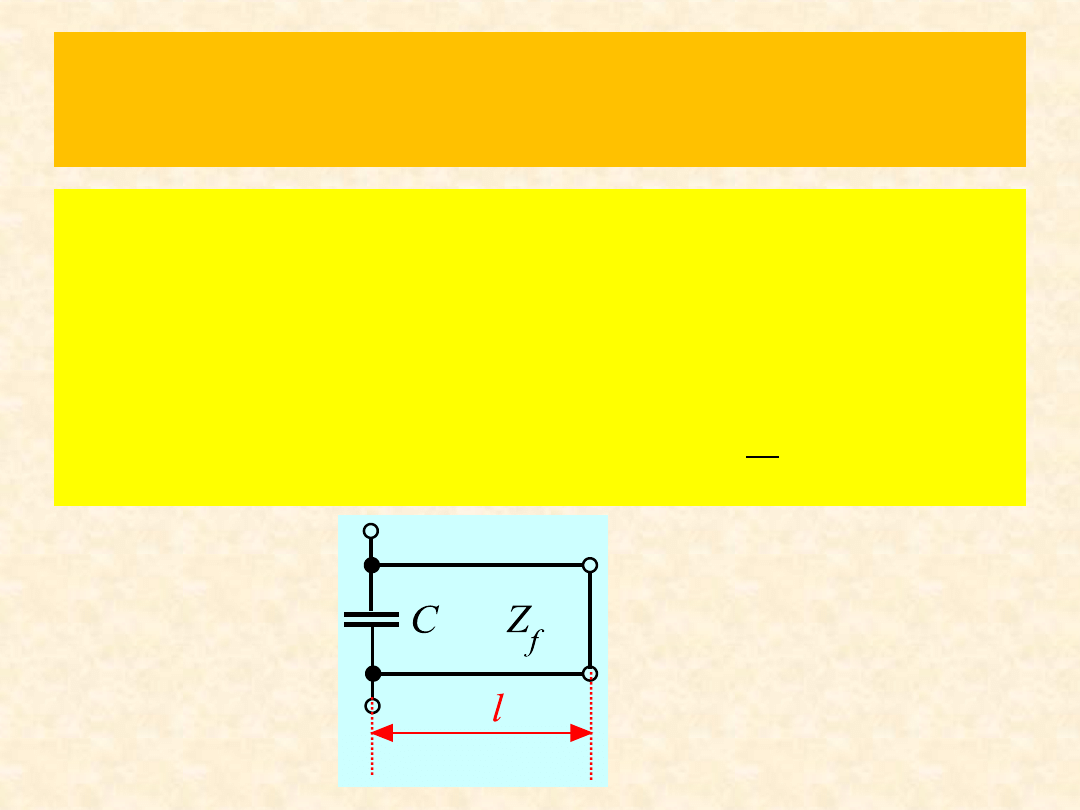
Zad.1

Wyznaczy długośd linii długiej zwartej na koocu,

jeśli po dołączeniu równolegle do wejścia linii
kondensatora o pojemności 50 pF powstał
obwód rezonansowy o częstotliwości
f

r

= 300MHz. Przyjąd :

8

3 10

,

75 .

f

m

c

Z

s



  

 

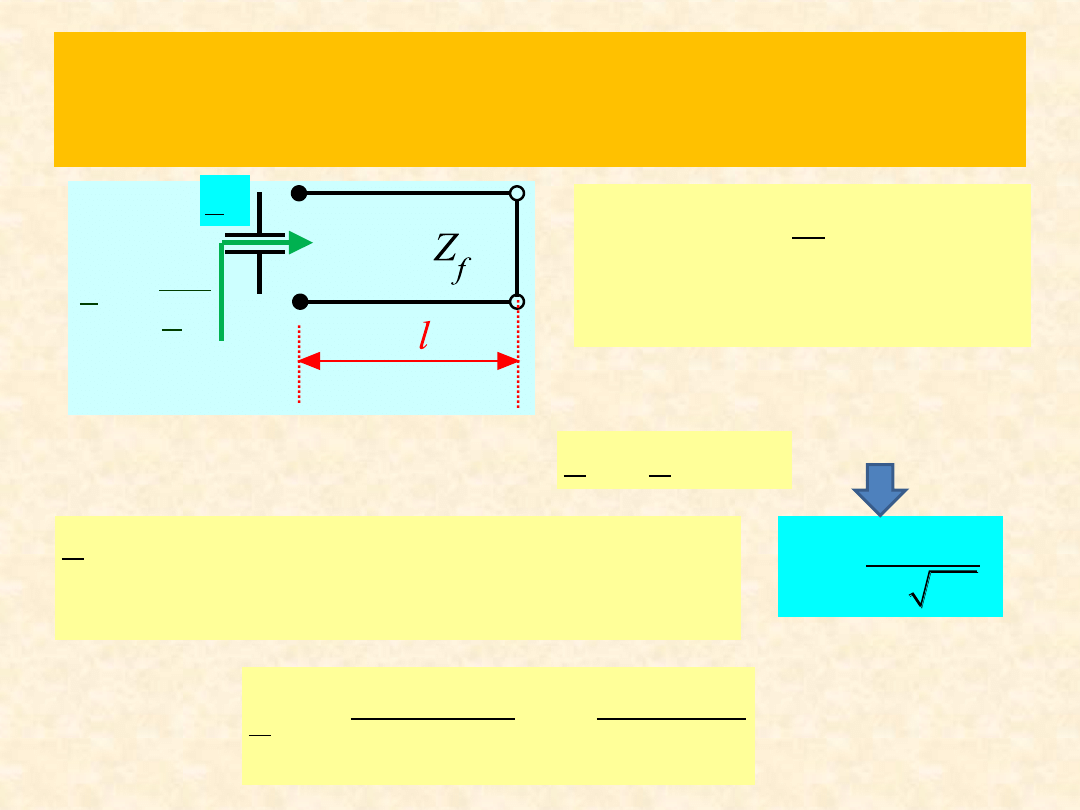
Rozwiązanie zad.1

8

3 10

,

75 ,

300 MHz,

50pF.

f

r

m

c

Z

s

f

C



  

 





1

we

we

Y

Z



6

12

j

j2

j2

300 10

50 10

0, 0942477 j

r

r

C

Y

C

f C

S

S





















 



Rezonans powstanie, jeśli

0.

C

we

Y

Y





1

1

j

j

(

)

(

)

we

f

f

Y

Z tg

l

Z tg

l







 

1

2

r

f

LC

















C

Y

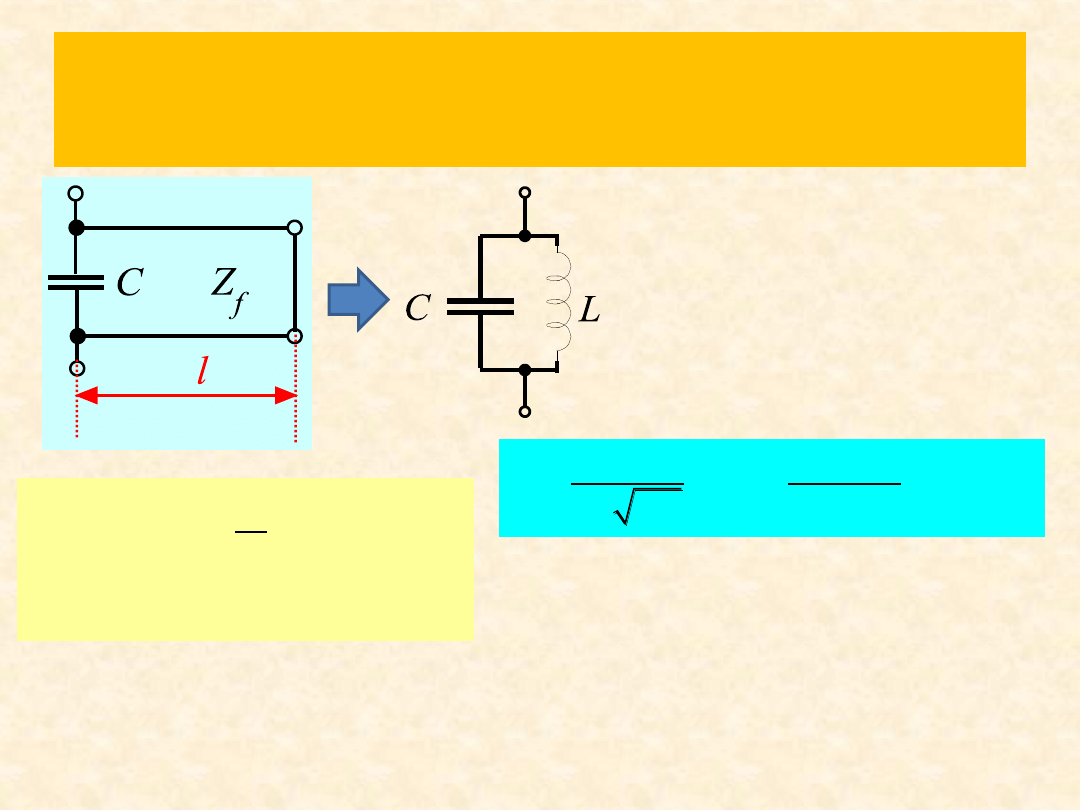
Rozwiązanie zad.1

8

3 10

,

75 ,

300 MHz,

50pF.

f

r

m

c

Z

s

f

C



  

 





2

2

1

1

5, 63nH

2

4

r

r

f

L

LC

Cf







 



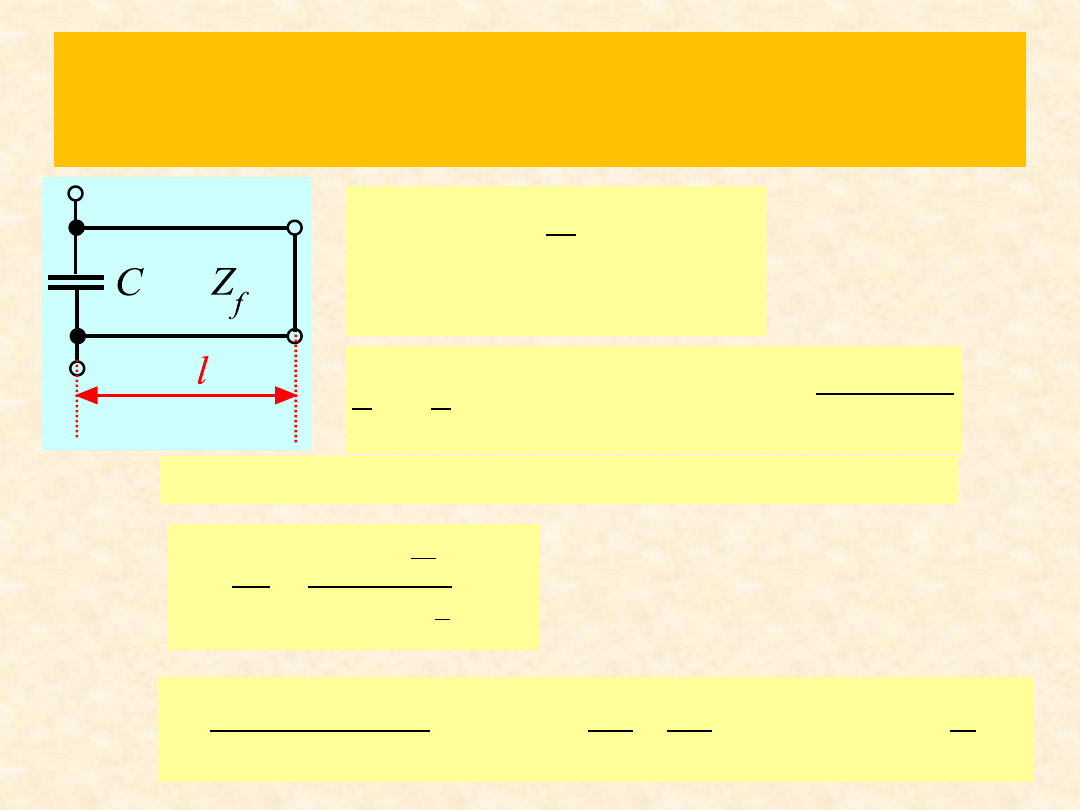
Rozwiązanie zad.1

8

3 10

,

75 ,

300 MHz,

50pF.

f

r

m

c

Z

s

f

C



  

 





1

0

0, 0942477 j

j

(

)

C

we

f

Y

Y

Z tg

l





 



(

)

0,1414

(0,1414)

0,14053

tg

l

l

arctg

k

















8 m

s

6 1

s

3 10

1m

300 10

r

c

f

















0,14053

0,14053

0, 022377+

m

2

2

k

k

l

k



























 







Zad. 2

Stratną linię długą obciążono na koocu

impedancją Z

k

= Z

f

. Wyznacz stałą tłumienia



,

jeśli wiadomo, że w odległości l = 18 km od
kooca toru amplituda napięcia w linii jest dwa
razy większa niż na koocu toru.

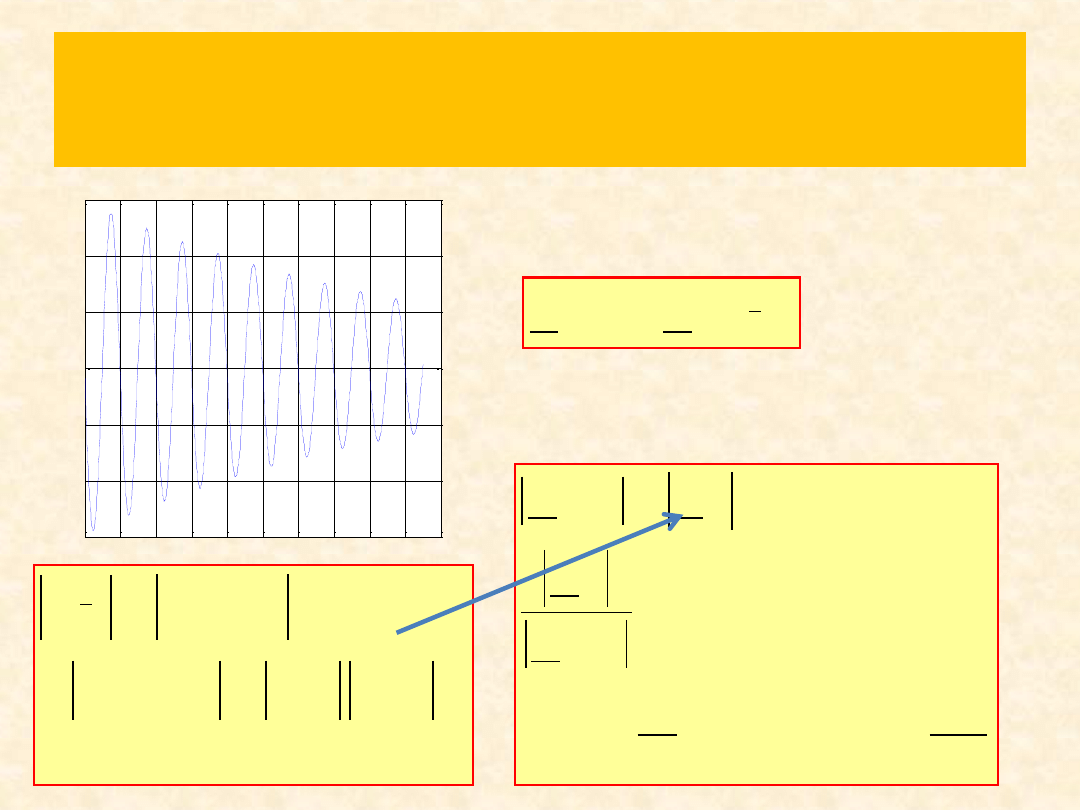
Rozwiązanie zad. 2

0

1

2

3

4

5

6

7

8

9

10

-1.5

-1

-0.5

0

0.5

1

1.5

Fala padajaca w linii dlugiej

x

N

a

p

ie

c

ie

( )

,

x

i

ip

U x

U e







 

18km

( )

,

2

( )

1

1

ln 2

0.0385

18

km

x

i

ip

ip

x

i

U x

U

e

U

e

e

U x

















 



 







+j

j

j

x

x

x

x

x

x

x

e

e

e

e

e

e

e



 





































W linii jest tylko fala padająca

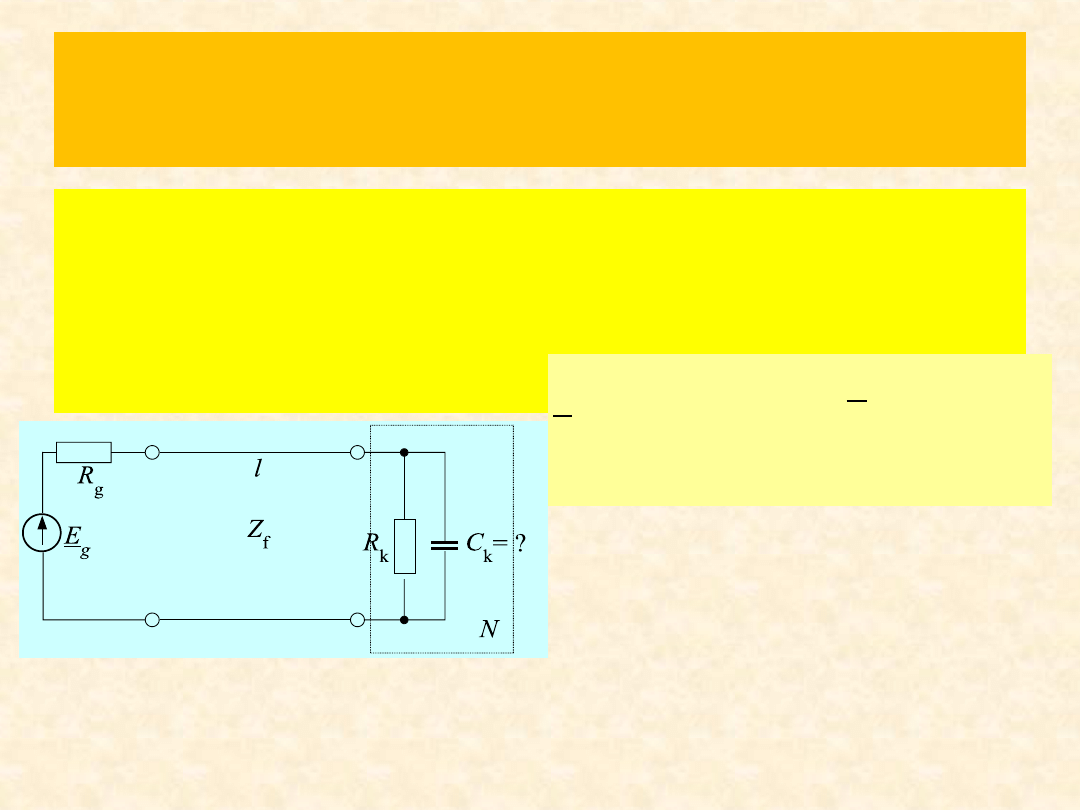
Zad. 3

Zadana jest linia bezstratna. Jaka jest wartośd

pojemności C

k

, jeśli wiadomo, że w dwójniku N

wydziela się moc czynna równa P=1/2W.

Dane:

8

10 ,

50 ,

=1,5 m,

4

25 ,

100 ,

3 10

/

g

f

g

k

f

E

j Z

l

R

R

c

m s







  

 





  

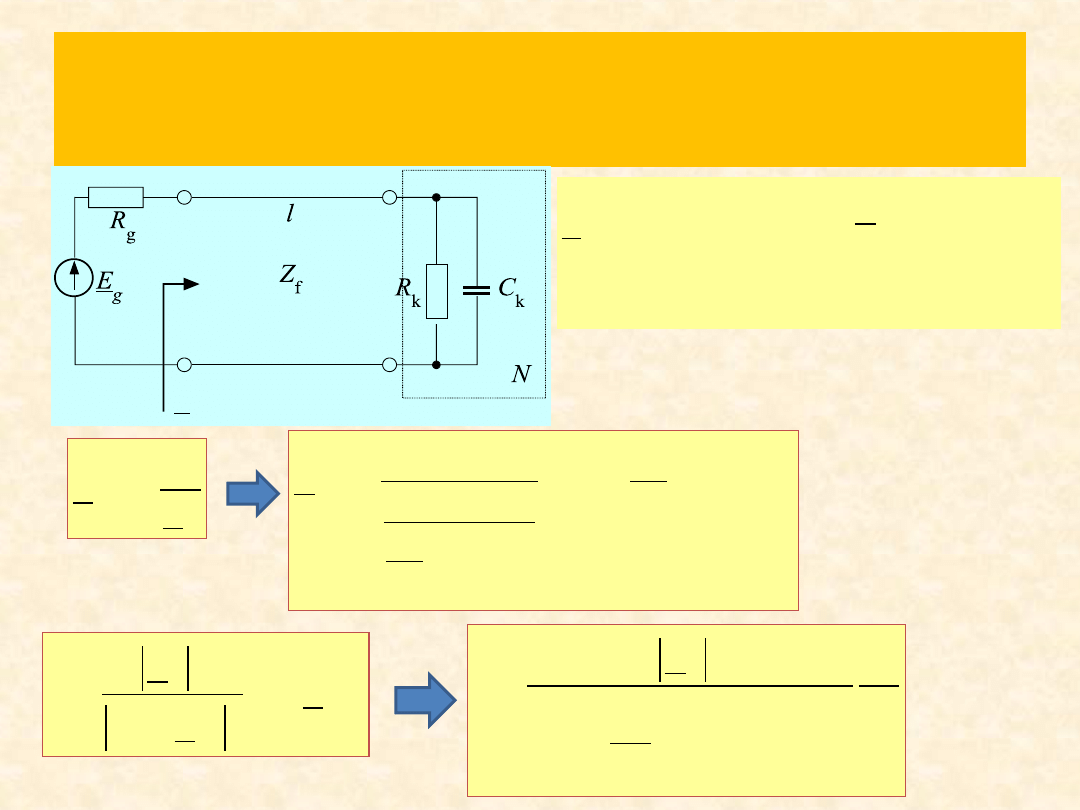
Rozwiązanie zad. 3

8

10 ,

50 ,

=1,5 m,

4

25 ,

100 ,

3 10

/

g

f

g

k

f

E

j Z

l

R

R

c

m s







  

 





  

we

Z

2

f

wej

k

Z

Z

Z



2

2

0

0

1

j

1

1

j

f

wej

f

k

k

k

k

Z

Z

Z

C

R

C

R

























 

2

2

Re

g

we

we

g

E

P

Z

R

Z









2

2

2

2

2

2

0

g

f

k

f

g

f

k

k

E

Z

P

R

Z

R

Z

C

R

























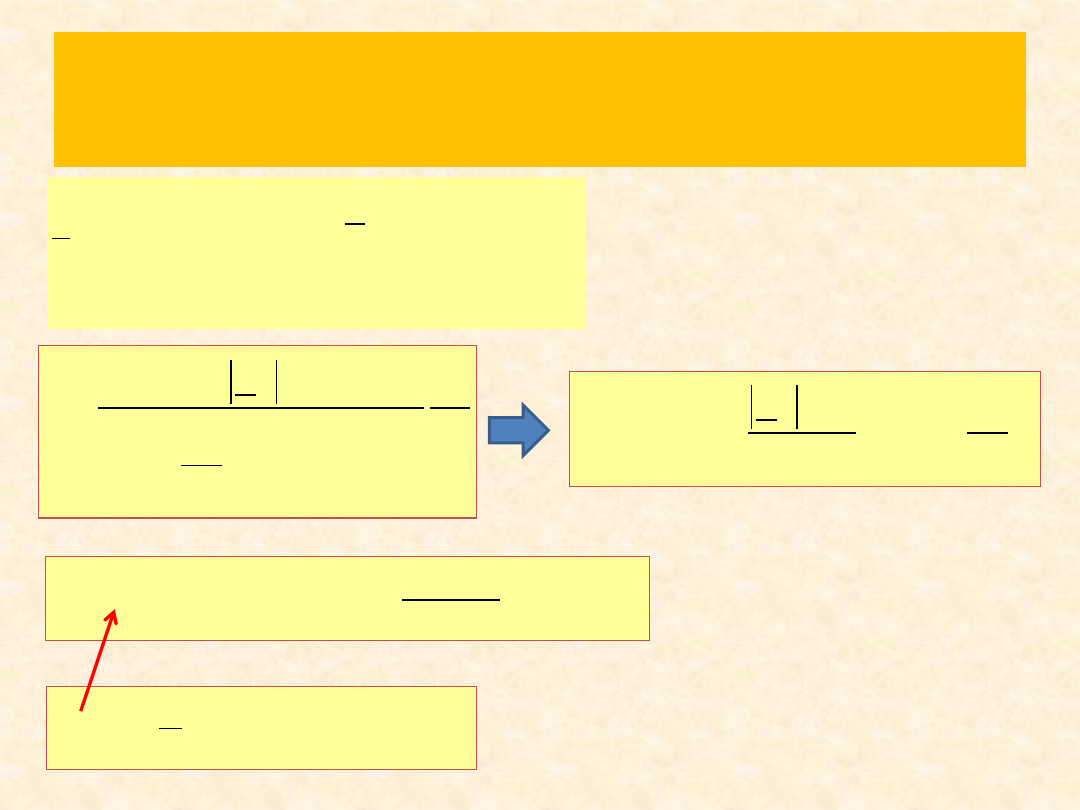
Rozwiązanie zad. 3





8

10 ,

50 ,

=1,5 m,

6m

4

25 ,

100 ,

3 10

/

g

f

g

k

f

E

j Z

l

R

R

c

m s









  



 





  





2

2

2

2

2

2

0

g

f

k

f

g

f

k

k

E

Z

P

R

Z

R

Z

C

R





























2

2

2

2

2

2

0

g

f

f

f

k

g

k

k

E

Z

Z

Z

C

R

PR

R





























2

2

0

9

1

2500

63, 67pF

5 10

f

k

k

Z

C

C



















8

0

2

10 ,

6 m

c

















Bezstratną linię długą o impedancji falowej

i długości obciążono

kondensatorem o pojemności .
Wyznaczyd prąd na początku linii jeżeli
napięcie na początku tej linii wynosi

f

50

Z



 



3

8

l





k

200 pF

C



 

p

,

i t

 

 

8

p

30 2 cos 10

V.

u t

t



Zad. 4

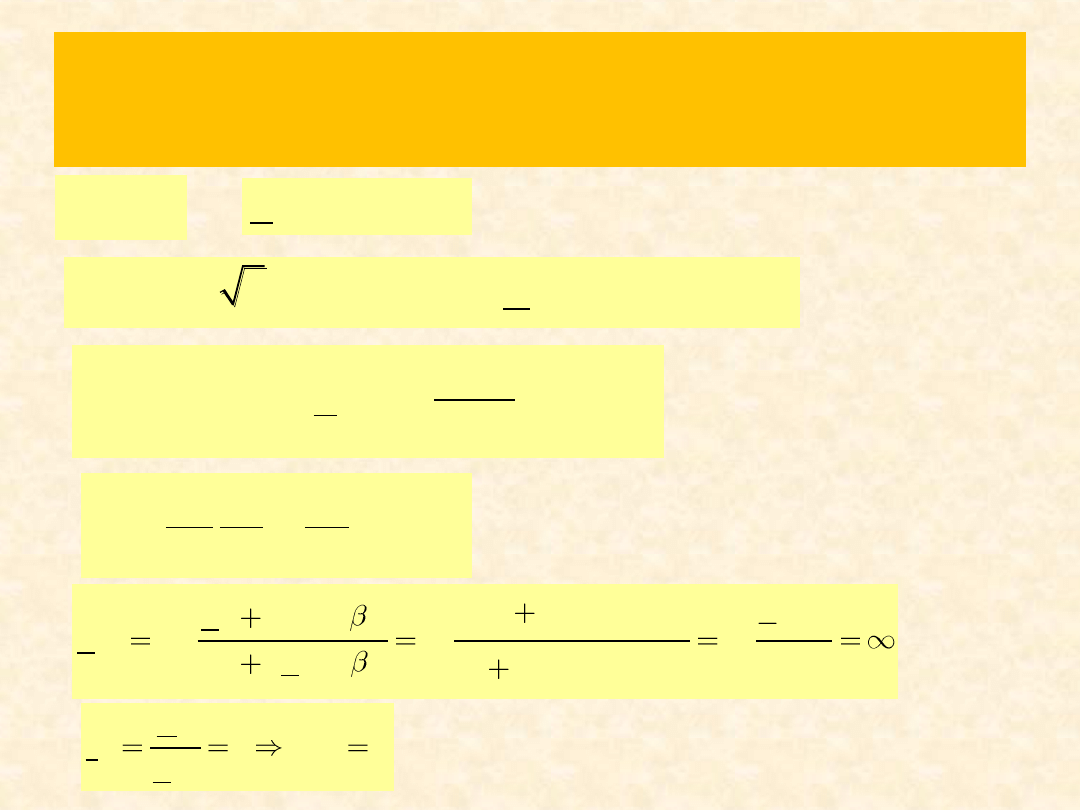
f

50

Z



 



0

2 3

3

(135 )

8

4

l

 











k

0

1

200 pF

j

j50

k

k

C

Z

C







 

 



 

p

?

i t



 

 

8

8

p

0

30 2 cos 10

V

30j,

10

p

u t

t

U











Rozwiązanie zad. 4

0

0

-j50

j50

135

100 j

50

50

0

50

j(-j50)

135

f

k

f

we

f

k

tg

Z

jZ tg

l

Z

Z

Z

jZ tg

l

tg

0

( )

0

p

p

p

we

U

I

i t

Z

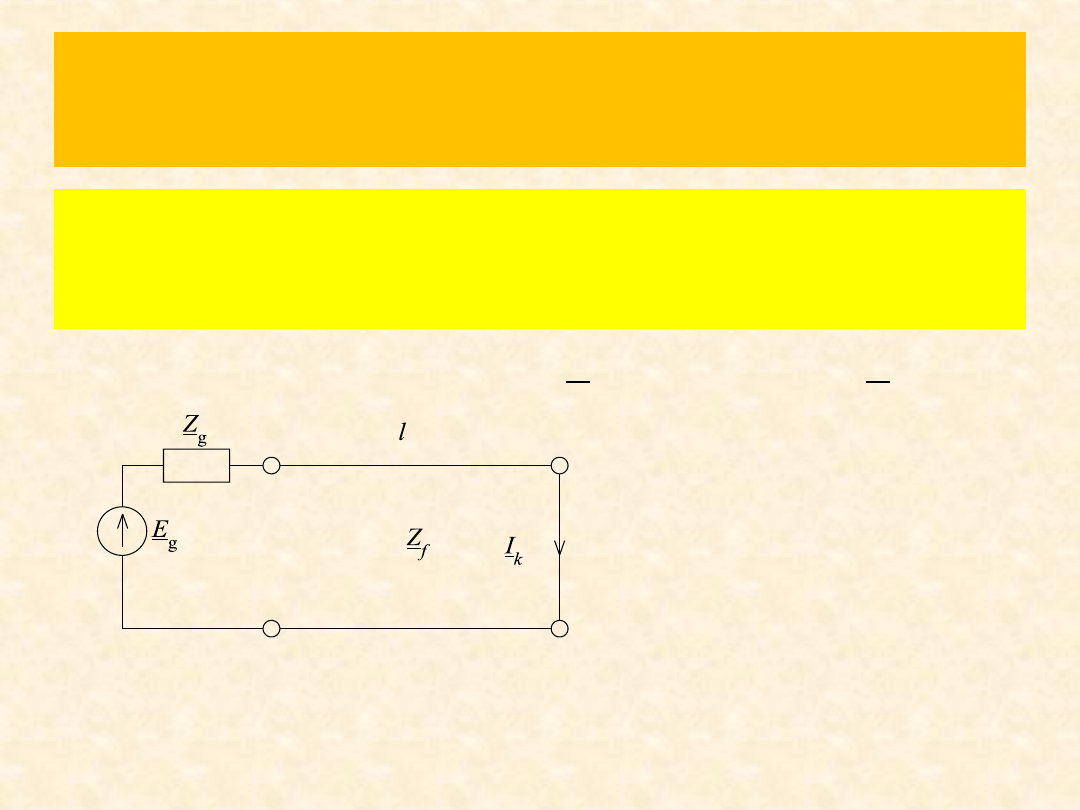
Zad. 5

Bezstratną linię długą zwarto na koocu. Obliczyd

wartośd skuteczną prądu I

k

. Dane:





3 ,

0.375

,

75 ,

60

80

,

100

g

g

f

m l

m Z

Z

j

E

V







 









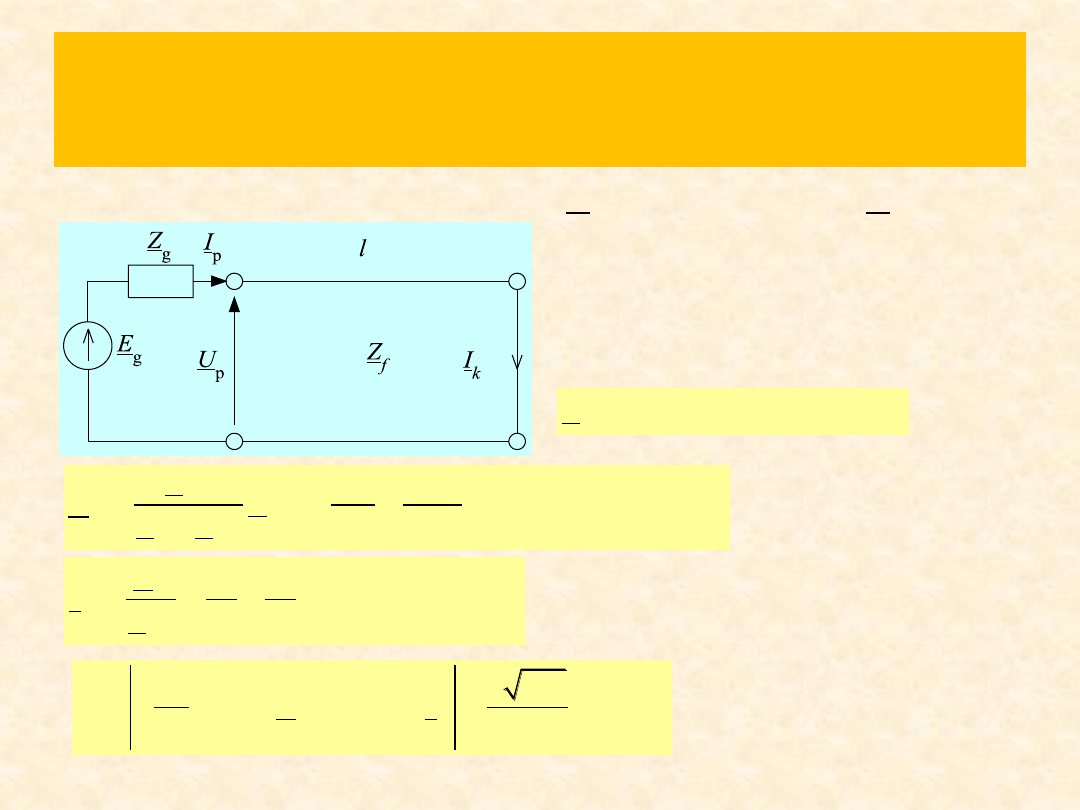
Rozwiązanie zad. 5

j

4 485

sin(

)

cos(

)

1.17A

75

p

p

k

f

I

l U

l I

Z





 











3 ,

0.375

,

75 ,

60

80

,

100

g

g

f

m l

m Z

Z

j

E

V







 









   

f

j

75j

,

wej

Z

Z tg

l













300

3600

j

-10,34+124,13j V

29

29

wej

g

p

g

wej

Z

U

E

Z

Z



 











48

4

j

1,66+0,138j A

29

29

p

p

wej

U

I

Z









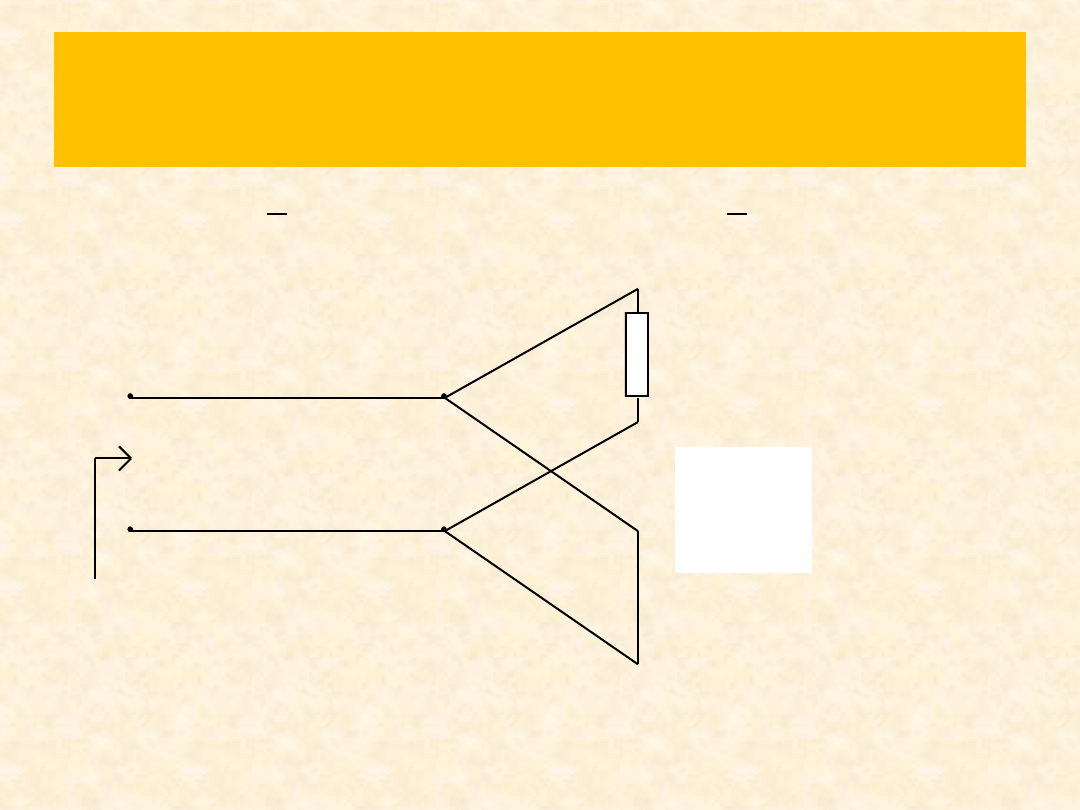
Zad. 6

Dobrać l

x

i Z

x

tak, aby w linii o impedancji Z

x

nie wystąpiła fala stojąca, tj



x

= 0, linie są bezstratne.

Z

x

Z

f

l

l

x

Z

f



x

=0

Z

f

=50



Z

k

=200



l=0.1



t

Z

k

50 ,

200 ,

0,1

f

k

Z

Z

l













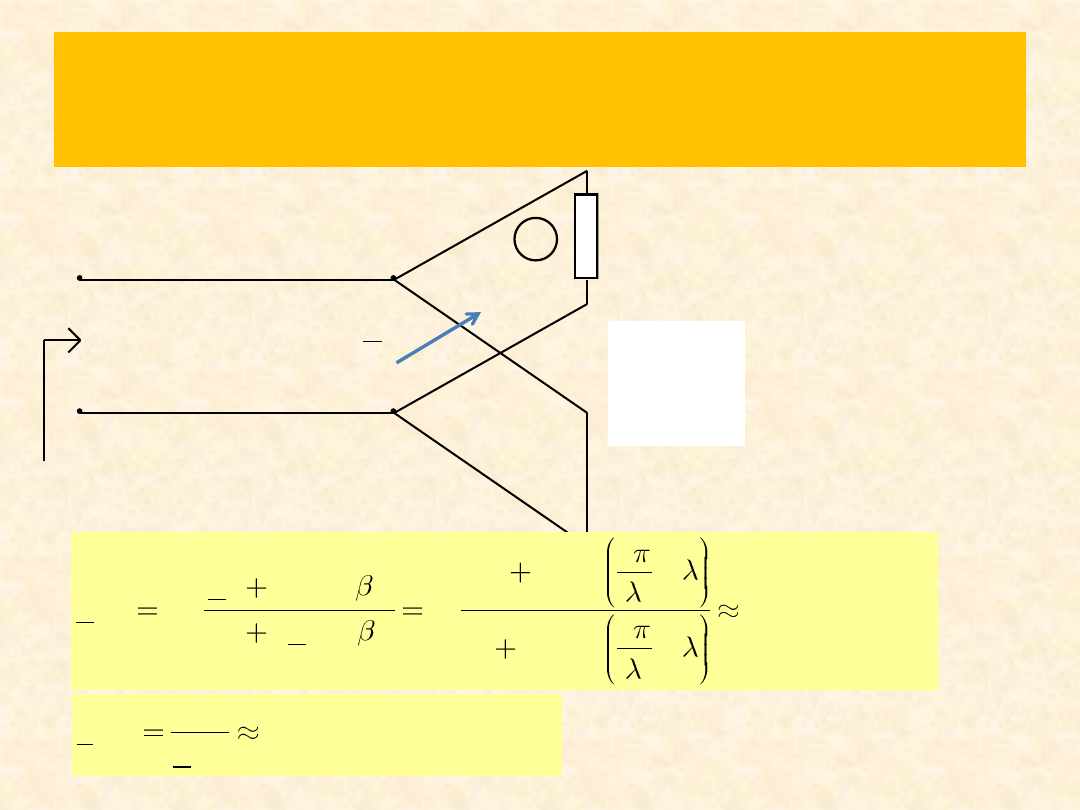
Rozwiązanie zad. 6

Z

x

Z

f

l

l

x

Z

f



x

=0

Z

f

=50



Z

k

=200



l=0.1



t

Z

k

50 ,

200 ,

0,1

f

k

Z

Z

l













1

2

200

50

01

50

32.35-57.69j Ω

2

50

200

01

f

k

f

we

f

k

j

tg

Z

jZ tg

l

Z

Z

Z

jZ tg

l

j

tg

1

we

Z

1

1

1

0.007395+0.0131876j

wej

we

Y

S

Z

1

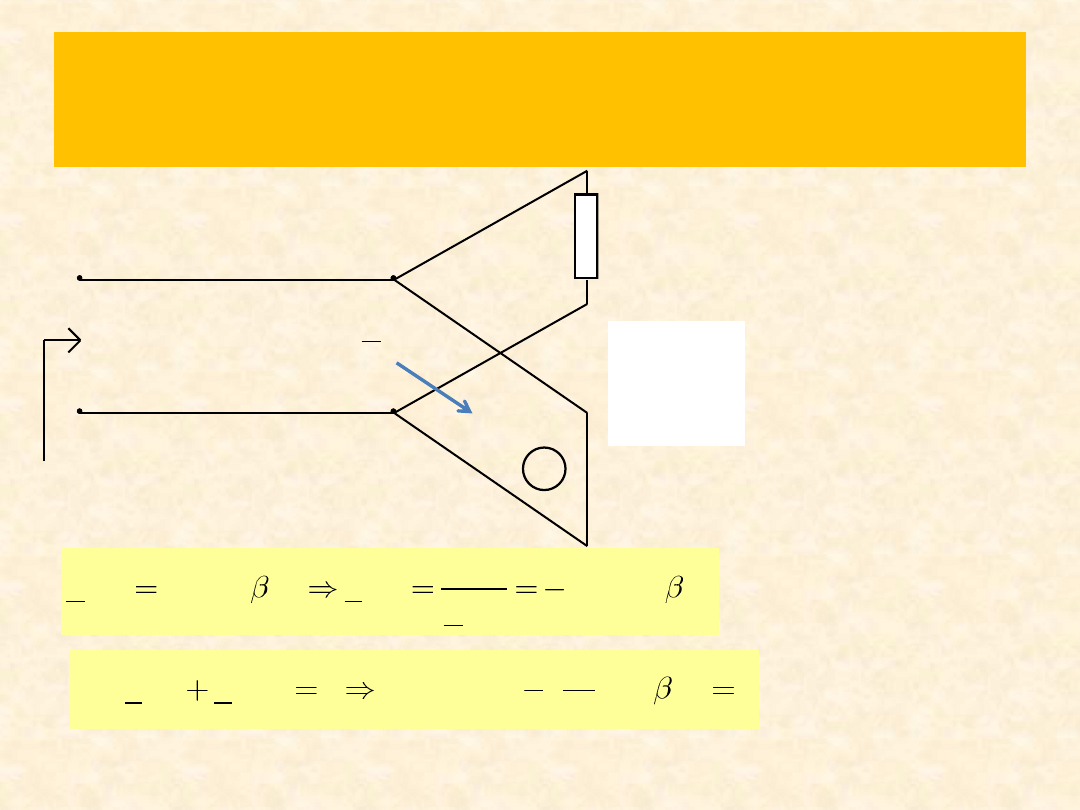
Rozwiązanie zad. 6

Z

x

Z

f

l

l

x

Z

f



x

=0

Z

f

=50



Z

k

=200



l=0.1



t

Z

k

50 ,

200 ,

0,1

f

k

Z

Z

l













2

2

2

1

j

f

x

f

x

we

we

we

Z

Z tg

l

Y

jY ctg

l

Z

2

we

Z

1

2

1

Im

0

0.0131876j

j

0

50

x

we

we

Y

Y

ctg

l

Jeśli linia o imp.
falowej Z

x

ma ma byd

dopasowana falowo, to
admitancja połączenia
równoległego linii 1 i 2
powinna byd czysto
rzeczywista (częśd
urojona tej admitancji
powinna byd równa
zeru).

2

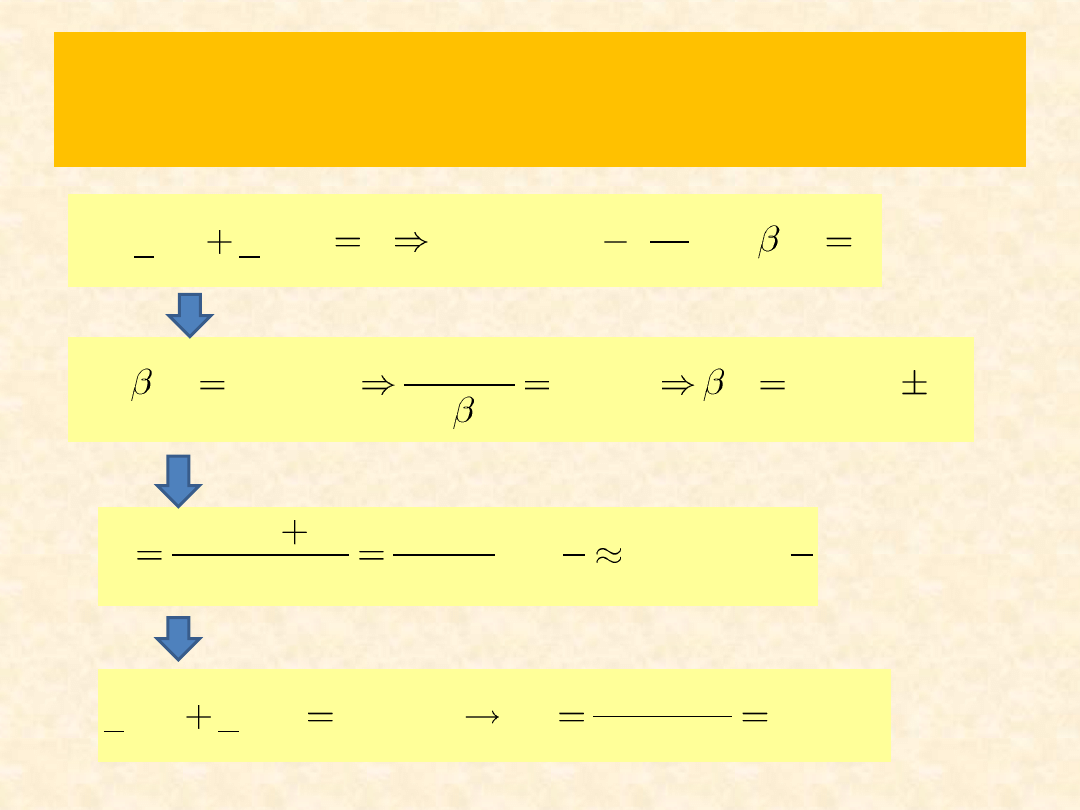
Rozwiązanie zad. 6

1

2

1

Im

0

0.0131876j

j

0

50

x

we

we

Y

Y

ctg

l

1

ctg(

)

0, 65938

1.5166

0,9879

kπ

x

x

x

l

l

tg

l

0,9879

π

0,9879

λ

λ

λ+

0.1572λ+

β

2π

2

2

x

k

l

k

k

x

1

2

1

.007395

Z

135.2 Ω

0.007395

wej

wej

Y

Y

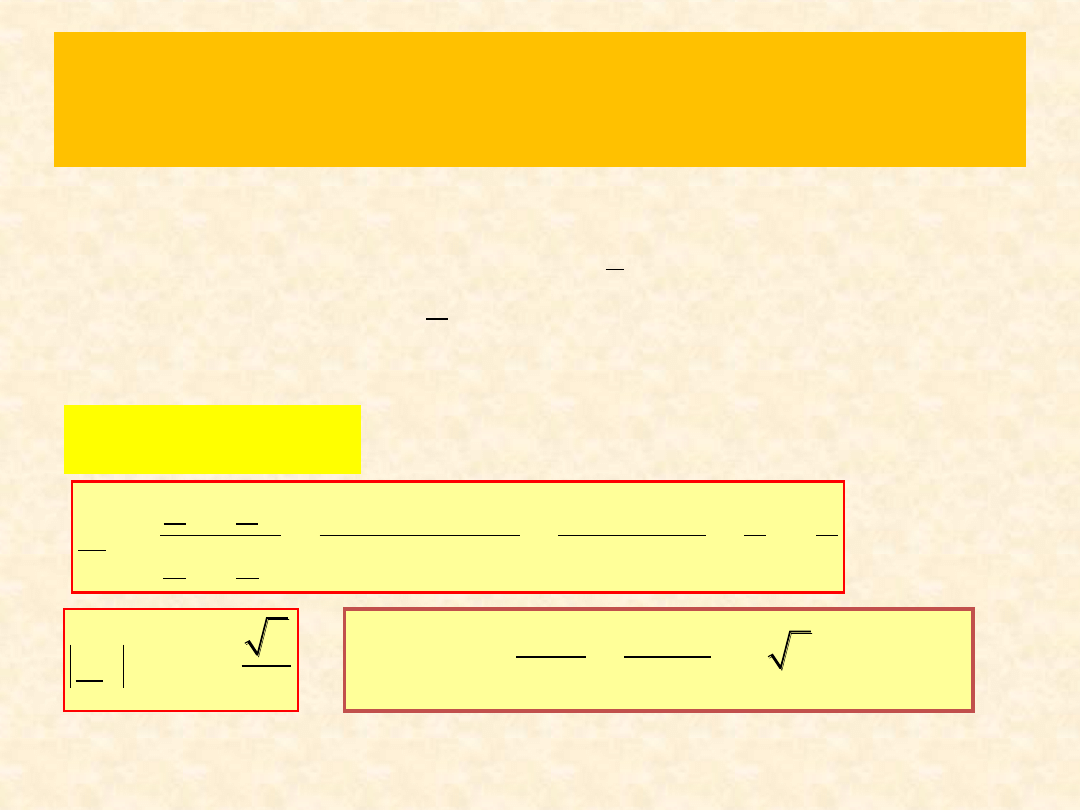
Zad. 7

Linia transmisyjna o pomijalnie małych stratach została

obciążona dwójnikiem o impedancji





k

50

j100 Ω

Z





Impedancja falowa linii

f

50Ω.

Z



 

Obliczyd współczynnik fali stojącej w tej linii.

Rozwiązanie

max

min

1

2 2

3

5,82.

1

k

k

U

Γ

WFS

U

Γ





 





 



50

j100 50

j100

1

1

j

50

j100 50

100

j100

2

2

k

f

k

k

f

Z

Z

Z

Z

















 









2

2

k

k







