M 16 - Pomiar współczynnika lepkości cieczy metodą Stokesa

1. Podstawy

Lepkość to właściwość rzeczywistych cieczy i plastycznych ciał stałych. Objawia się pojawieniem
się siły tarcia pomiędzy warstwami cieczy, poruszającymi się równolegle względem siebie z
różnymi co do wartości prędkościami. Warstwa poruszająca się szybciej działa przyspieszająco na
warstwę poruszającą się wolniej i odwrotnie. Pojawiające się wtedy siły tarcia wewnętrznego
skierowane są stycznie do powierzchni styku tych warstw.

Lepkość można ilościowo scharakteryzować współczynnikiem η równym wartości siły stycznej,
która przyłożona do jednostki powierzchni spowoduje jednostajny, laminarny przepływ z
jednostkową˝ prędkością.

Sir George Stokes wyliczył w 1851 roku wzór na siłę tarcia działającą na kulkę o promieniu r,
poruszającą się z prędkością v w płynie o współczynniku lepkości η . Wynosi ona:



F =−6  r v (1.1)

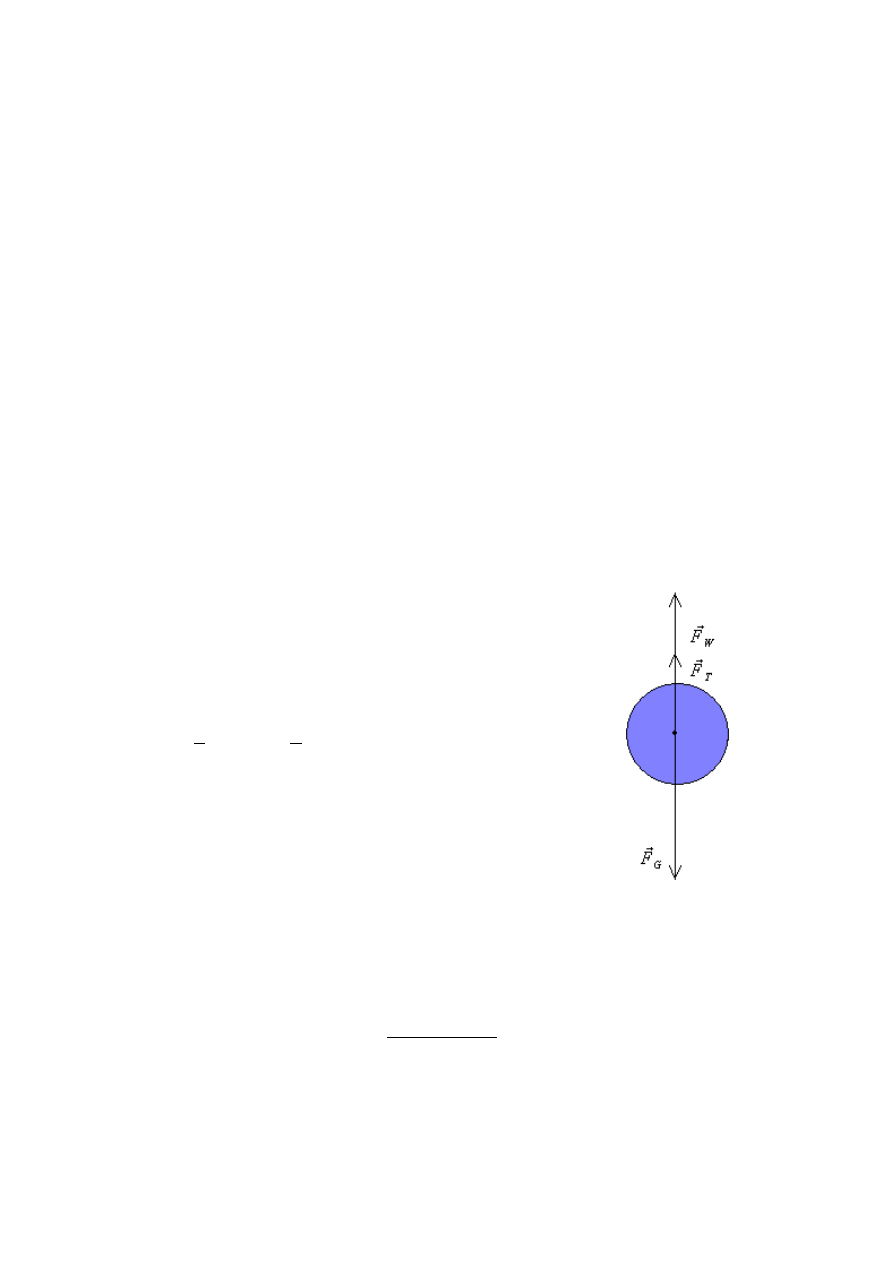
Na kulkę opadającą z prędkością

v

w płynie o współczynniku lepkości η w polu grawitacyjnym

Ziemi działają trzy siły: ciężkości 

F

G

, wyporu



F

W

oraz lepkości 

F

T

. Zobrazowano to na

Rys.1.

Kulka wrzucona do płynu po pewnym czasie zaczyna
poruszać się ruchem jednostajnym. Dzieje się tak dlatego, że
po pewnym czasie wszystkie siły działające na nią się
równoważą i zgodnie z I zasadą dynamiki kulka osiąga stałą
prędkość taką, że 

F

G

= 

F

W

 

F

T

.

Możemy nieco rozwinąć ten warunek, wiedząc, jak wyrażają
się poszczególne siły w powyższym wzorze:



k

⋅

4
3



r

3

g =

p

⋅

4
3



r

3

g6  r v (1.2)

gdzie



k

to gęstość materiału, z jakiego zbudowana jest

kulka, 

p

to gęstość płynu, w jakim się porusza, r to jej

promień, v - prędkość, a g - przyspieszenie ziemskie.

Oznacza to, że aby wyznaczyć współczynnik lepkości płynu
badając ruch opadającej w nim kulki, musimy znać gęstość
tego płynu, gęstość materiału, z jakiego wykonana jest kulka,
jej promień oraz prędkość.

Rys.1. Rozkład sił działających na kulkę
opadającą w ośrodku lepkim.

Po kilku prostych przekształceniach (przyjmując, że prędkość = droga/czas), dostajemy wzór na η:

=

2 

k

−

p



gr

2

t

9l

(1.3)

gdzie l to droga, jaką przebyła kulka w czasie t.

2. Schemat i sposób wykonania ćwiczenia

Wiemy już, jak teoretycznie można doprowadzić do sytuacji, w której można zmierzyć
współczynnik lepkości - musimy wrzucić kulkę z materiału o znanej gęstości do płynu, którego
współczynnik lepkości chcemy zbadać, a następnie, gdy kulka zacznie się poruszać ruchem
jednostajnym, zmierzyć czas jej przelotu na ustalonej przez nas drodze. Należy też zmierzyć jej
promień.

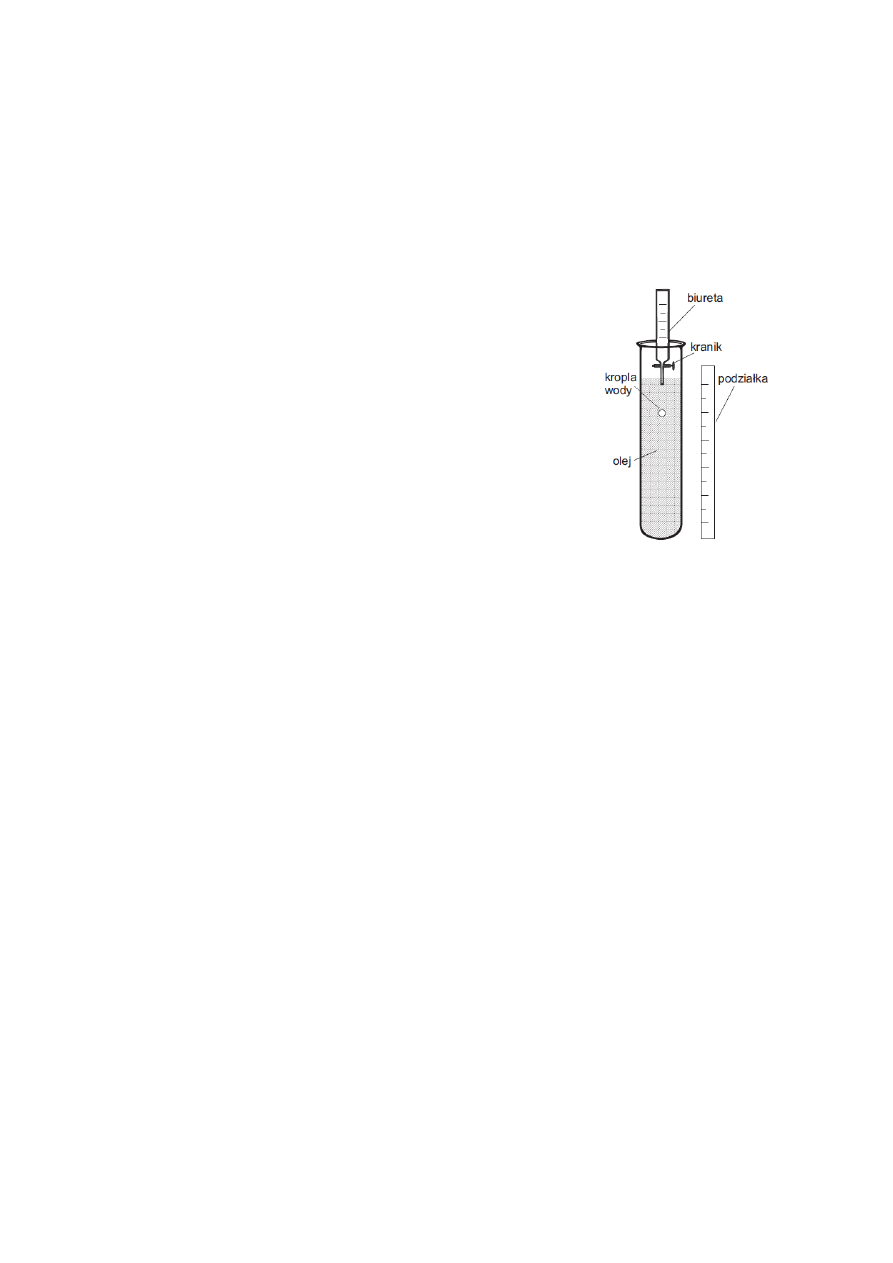
Aby pomiar był dokładny, najlepiej wrzucić kilka takich samych
kulek i zmierzyć czas dla każdej z nich. Rozwiązanie stosowane
w I PF pokazano na Rys. 2.

Do cylindra napełnionego badaną cieczą (olejem parafinowym)
wpuszczane są krople wody destylowanej. Za pomocą kranika
na biurecie z wodą można ustalić stałe tempo wypływu kropel.
W ten sposób wiedząc, ile wody w biurecie ubyło dla danej
ilości kulek, możemy wyliczyć objętość pojedynczej kulki, a
następnie również jej promień. Spadające krople poruszają się na
tle podziałki, dzięki czemu można wyznaczyć drogę spadania
kulki dla której będziemy mierzyć czas. Gęstość oleju możemy
wyznaczyć, korzystając z naczyń połączonych i znając dokładną
gęstość wody. Dzięki temu będziemy mieć wszystkie potrzebne
dane do wyliczenia η.

Rys. 2. Schemat wykonania ćwiczenia

Przebieg pomiaru powinien wyglądać następująco: mierzymy poziomy wody i oleju w naczyniach
połączonych, po czym odczytujemy temperaturę powietrza w pracowni za pomocą termometru
(dzięki temu bardzo dokładnie będziemy znać gęstość wody). Napełniamy biuretę wodą, a
następnie wsuwamy jej końcówkę poniżej poziomu oleju. Z wyczuciem odkręcamy kranik, aby
wpuszczane do oleju krople wody opadały w tempie pozwalającym na pomiary. Poziom, od którego
mierzymy czas należy obrać w miarę głęboko pod powierzchnią tak, aby kulki poruszały się
ruchem jednostajnym. Odczytujemy poziom wody na podziałce biurety przed spadnięciem
pierwszej kulki z naszej serii pomiarowej (i zapisujemy). Dla ok. 20 kulek (należy koniecznie
zapisać ich ilość!) mierzymy czas na ustalonej drodze l. Po spadnięciu ostatniej kulki z serii
ponownie odczytujemy poziom wody na podziałce biurety (i zapisujemy). Pomiary możemy
powtórzyć założywszy inną końcówkę - dzięki temu kulki będą miały inny promień.

3. Opracowanie wyników

Naszym celem jest wyznaczenie współczynnika lepkości oleju dla każdej serii pomiarowej. W tym
celu do wzoru (1.3) potrzebujemy podstawić wyznaczone w ćwiczeniu wielkości: gęstość wody,
gęstość oleju, promień średniej kropli dla danej serii, średni czas ruchu kropli oraz drogę, jaką
krople przebywały.

I. Wyznaczenie gęstości oleju.

Mając poziomy wody

h

k

i oleju

h

p

odczytane na naczyniach połączonych oraz znając dokładnie

gęstość wody 

k

w danej temperaturze, możemy wyznaczyć gęstość oleju 

p

za pomocą

wzoru:



p

=

k

h

k

h

p

(3.1)

II. Wyznaczanie promienia kropel.

Znając poziomy wody w biurecie przed rozpoczęciem i po zakończeniu serii pomiarowej, znamy
sumaryczną objętość wody, jaka wypłynęła w danej serii pomiarowej. Wiemy zatem, że n razy
objętość średniej kropli = objętość wody, jaka ubyła w biurecie. Zapisując to za pomocą wzoru:

n⋅

4
3



r

3

=

V (3.2)

gdzie V to objętość wody, jaka ubyła w biurecie podczas pomiaru (czyli różnica zapisanych przed i
po poziomów), r - średni promień pojedynczej kulki, a n - liczba kulek.
Po przekształceniu:

r =

3



3⋅V

4  n

(3.3)

Aby wyznaczyć niepewność pomiaru r znając niepewność pomiarową V, korzystamy ze wzoru:



r =

∣



∂

r

∂

V



∣



V =

3



3

4  n

⋅

1
3

V

−

2

3

⋅

V (3.4)

III. Wyznaczanie średniego czasu spadania kulki na ustalonej drodze l:

Wyliczamy średni czas spadania t jako średnią arytmetyczną wszystkich n pomiarów, ponieważ
bierzemy pod uwagę średnią kroplę.
Niepewność pomiarowa czasu t to suma odchylenia standardowego naszej serii pomiarowej oraz
błędu stopera (czyli 0,01s) t=S

t



0,01 s

Wzór na odchylenie standardowe:

S

t

=



1

nn−1

∑

i=1

n



t

i

−

t 

2

(3.5)

Gdzie t

i

to i-ty pomiar czasu, a t - czas średni.

IV. Wyznaczenie współczynnika lepkości

Podstawiamy wyznaczone wielkości do wzoru na współczynnik lepkości (1.3).
Aby wyznaczyć niepewność pomiarową η, korzystamy z różniczki zupełnej (w dalszej części wzoru
wyliczone zostały poszczególne pochodne). Przyjęto, że do niepewności pomiarowej η wkład dają
wyznaczone uprzednio niepewności t i r.

 =

∣



∂
∂

r



∣



r 

∣



∂

∂

t



∣



t=

4 

k

−

p



gr t

9l



r 

2

k

−

p



gr

2

9l



t (3.6)

Jeżeli wykonaliśmy więcej niż jedną serię pomiarową, to dla każdej serii osobno powtarzamy punkt
II, III i IV. W ten sposób otrzymamy kilka wartości współczynnika lepkości, które należy porównać
ze sobą. Czy zgadzają się ze sobą w ramach niepewności pomiarowych? Jeżeli nie, to co mogło być
przyczyną?
W sprawozdaniu powinien znaleźć się wstęp teoretyczny, w którym należy zawrzeć wszystkie
wzory, których używamy do opracowania wyników.