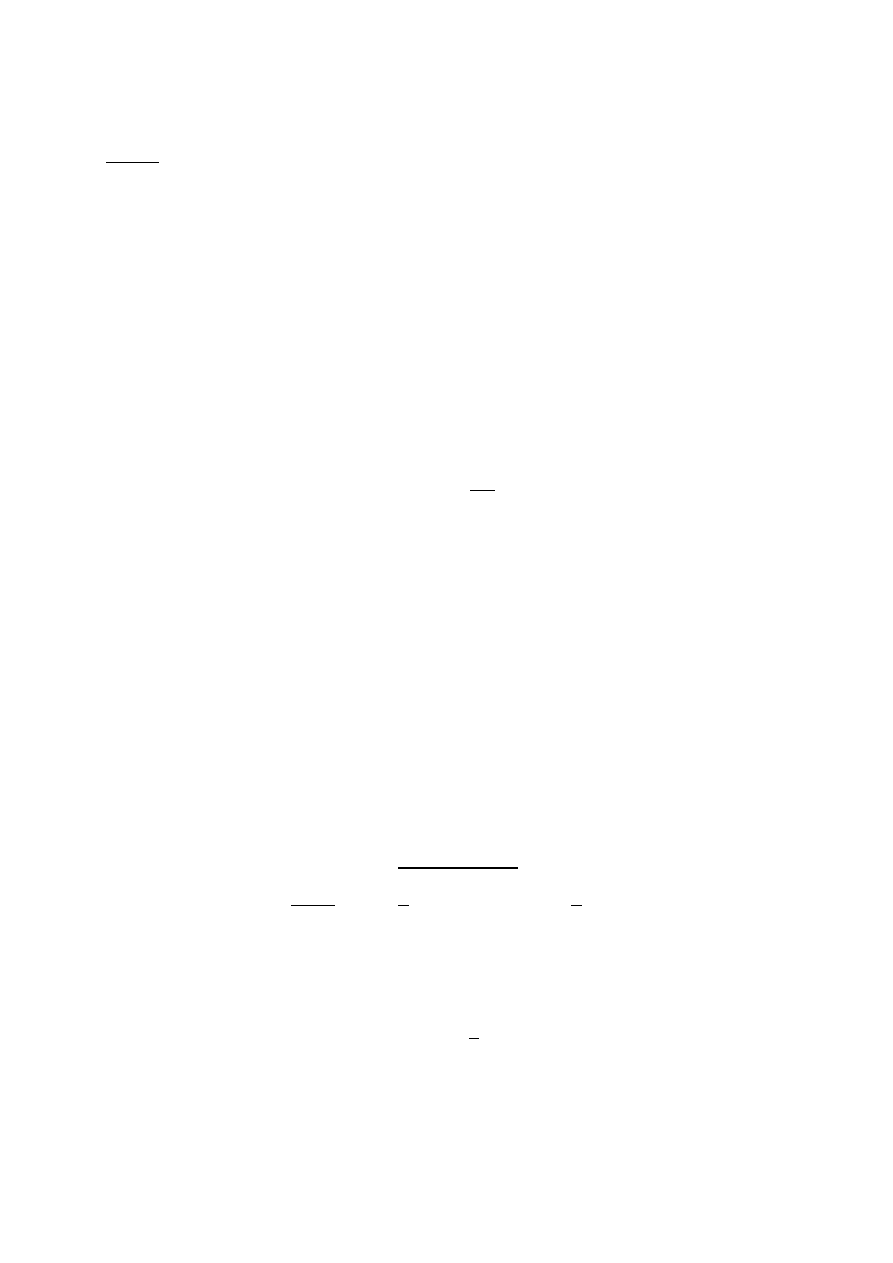
2) 

Test zgodności λ Kołomogorowa 

Model I 

Założenia: 

- populacja generalna ma dowolny ciągły rozkład Ω, 

- próba losowa o dużej liczebności (n≥30), 

- F(x) – dystrybuanta rozkładu populacji, 

- F

0

(x) – hipotetyczna ciągła dystrybuanta, 

- weryfikacja na podstawie próby losowej hipotezy H

0

: F(x) = F

0

(x) 

Wyniki próby grupujemy w stosunkowo wąskie przedziały o prawych końcach x

j

 oraz liczebnościach 

n

j

. Obliczamy empiryczną dystrybuantę F

n

(x) ze wzoru: 

 

 

( 

 

)  

 

  

 

 

Gdzie n

sk

 – jest to liczebność skumulowana, czyli suma wszystkich klas do danej, potrzebnej nam 

klasy, np.: 

Klasy nj: 

 

1

,

3

,

5

,

7

,8 

Liczebność nsk:  

1,4,9,

16

,24 

Czyli jest to liczebność skumulowana do początku aż do xk obliczana ze wzoru: 

 

  

∑  

 

   

 

 

Z rozkładu hipotetycznego wyznaczamy dla każdego xj wartość teoretycznej dystrybuanty F(x), np. 
F(x)=F(uj), przy czym: 

 

 

 

 

 

   ̅

 

         √

 
 

∑( 

 

   ̅)

 

 

   

 

 

      ̅  

 
 

∑  

 

 

 

 

   

 

Ostatecznie wyznaczana jest wartość statystyki lambda z zależności: 

          

 

( )  

     √  

 

 

MODEL II (test Kolomogorowa – Smirnowa) 

Założenia: 

- dwie populacje generalne mają dowolny ciągły rozkład omega, 

- dwie próby losowe o dużej liczebności (n1≥30, n2≥30), 

- F1(x), F2(x) – dystrybuanty rozkładu populacji, 

- weryfikacja na podstawie prób losowych hipotezy H0: F1(x) = F2(x). 

 

Wyniki prób grupujemy w stosunkowo wąskie przedziały o prawych końcach xj oraz liczebnościach nj. 
Obliczamy empiryczne dystrybuanty Fn1(x), Fn2(x)  za wzorów: 

 

 

  

( 

 

)  

 

   

  

     

  

( 

 

)  

 

   

  

 

Gdzie n_sk: 

 

   

∑  

  

   

     

   

∑