Nazwisko i imię, grupa

Katowice, dn……………..

rok I, sem. 01, r.akad. 2014/2015

ĆWICZENIE PROJEKTOWE Z PRZEDMIOTU

BUDOWNICTWO PRZEMYSŁOWE

Temat: BELKA PODSUWNICOWA

Dane projektowe:

L

0

= 21,00

m

rozpiętość wiązara

H

= 18,00

m

wysokość hali

a

= 6,00

m

rozstaw słupów głównych

A

= 150,00

m

długość hali

Q

= 200,00

kN

minimalny udźwig suwnicy

A4

grupa natężenia pracy

18G2A, St3S

rodzaj stali

Kędzierzyn Koźle

lokalizacja hali

SD75

rodzaj szyny

Strona 1

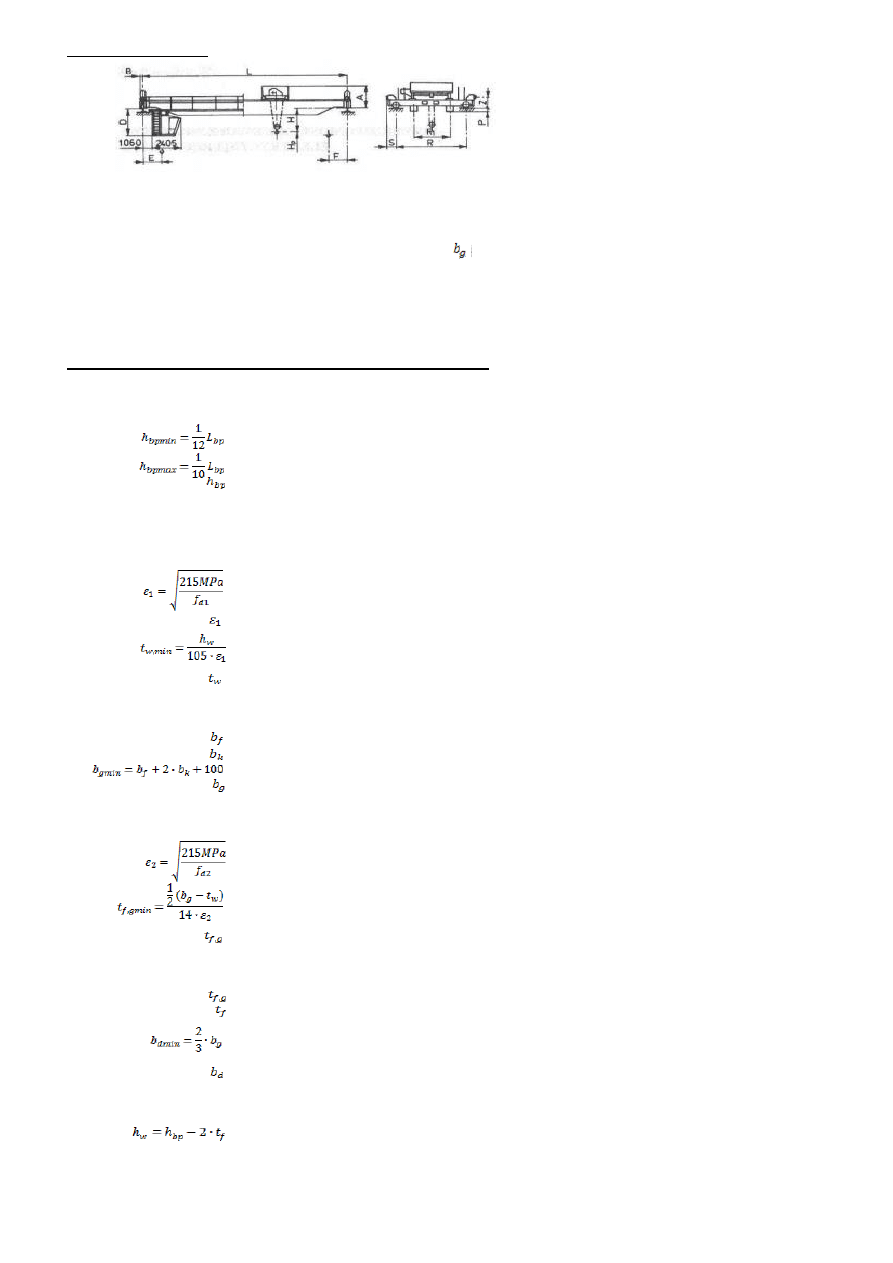
1. Charakterystyka suwnicy.

Udźwig suwnicy

Q 200,00

Rodzaj suwnicy

Suwnica jednohakowa pomostowa, natorowa

Masa suwnicy

G

S

27,30

kN

Nacisk koła

P

max

186,00

kN

Rozstaw kół suwnicy

R 5,00

m

=

0,42 mm

n 2,00

h

s

=

0,3 m

e

h

1,10

m

B =

0,245

L

S

19,07

m

L

0

-2(

h

s+

B

+

b

g

)

=

19,07

2. Ukształtowanie przekroju poprzecznego belki podsuwnicowej i tężnika podłużnego.
2.1. Kształtowanie przekroju poprzecznego belki podsuwnicowej.
2.1.1. Ustalenie optymalnej wysokości belki podsuwnicowej:

L

bp

= 6,00

m

rozpiętość belki podsuwnicowej

= 0,50

m

= 0,60

m

= 0,60

m

2.1.2. Ustalenie grubości środnika:

f

d1

= 305,00

MPa

dla stali 18G2A

h

w

=h

bp

= 0,60

m

wysokość środnika

= 0,84

= 0,84

= 6,81

mm

przyjęto

= 16,00

mm

grubość środnika

2.1.3. Ustalenie szerokości pasa górnego:

= 210,00

mm

= 50,00

mm

= 410,00

mm

= 420,00

mm

2.1.4. Ustalenie grubości pasa górnego:

f

d2

= 295,00

MPa

= 0,85

= 16,90

mm

= 20,00

mm

2.1.5. Ustalenie szerokości pasa dolnego:

= 20,00

mm

= 20,00

mm

= 280,00

mm

przyjęto

= 300,00

mm

2.1.6. Ustalenie wysokości środnika:

= 560,00

mm

Ilość kół suwnicy po jednej
stronie mostu

Minimalna odległość haka od toru
suwnicy
Rozpiętość mostu suwnicy

Strona 2

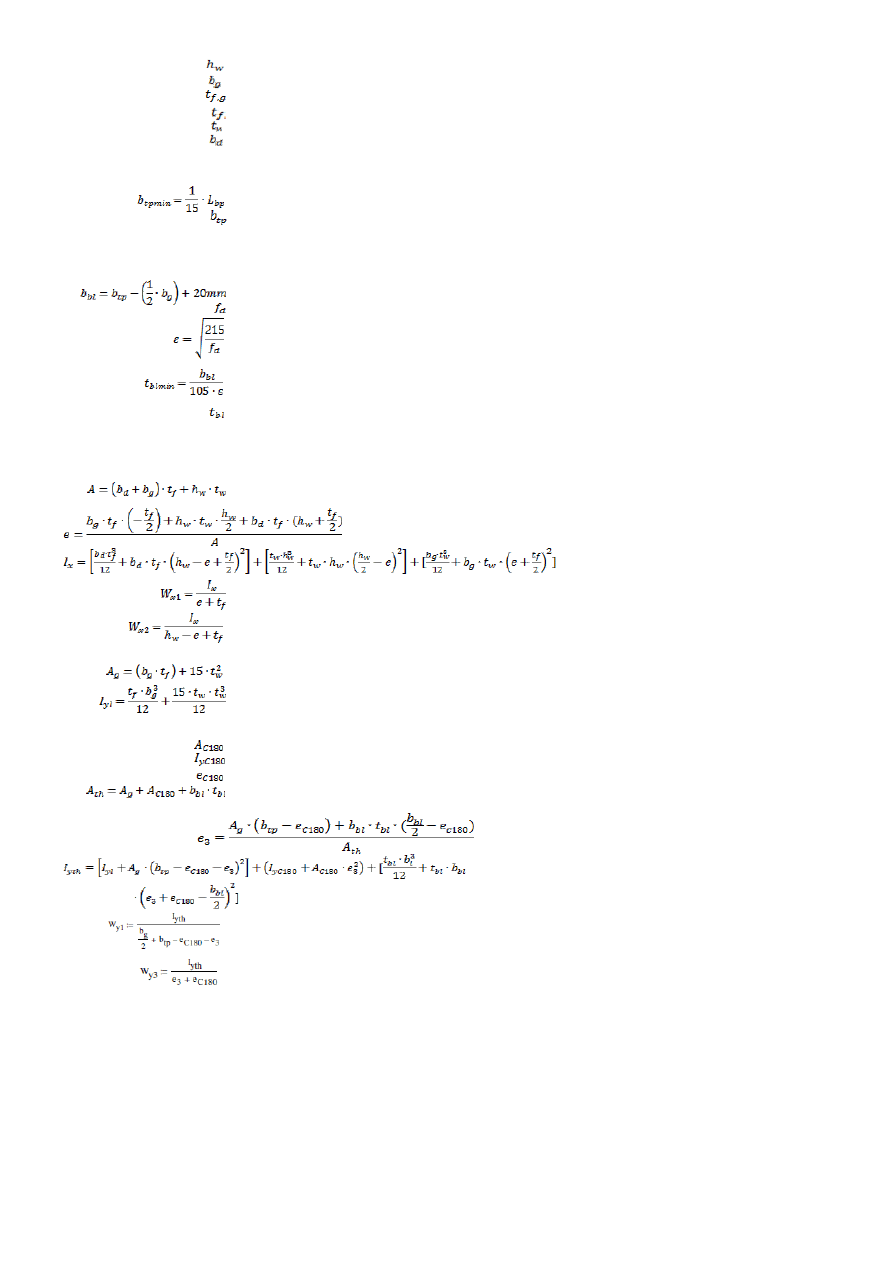
2.1.7. Zestawienie wymiarów belki podsuwnicowej:

= 560,00

mm

= 420,00

mm

= 20,00

mm

= 20,00

mm

= 16,00

mm

= 300,00

mm

2.1.8. Ustalenie odległości od osi szyny do krawędzi blachy żeberkowej:

= 0,40

m

= 0,80

m

2.1.9. Ustalenie wymiarów blachy żeberkowej:

= 610,00

mm

= 215,00

MPa

= 1,00

= 5,81

mm

przyjęto

= 6,00

mm

2.2. Charakterystyka przekroju belki podsuwnicowej.
2.2.1. Belka pionowa:

= 0,02

m

= 250 mm

=

0,001311 m4

= 0,005

m3

= 0,004

m3

2.2.2. Pole przekroju pasa górnego i współpracującej części środnika:

= 0,012

m2

= 0,0001236

m4

2.2.3. Tężnik hamowny:

= 28

cm2

=

114

cm4

= 1,92

cm

= 0,019

m2

=

0,5670064 m

=

0,001987 m4

= 0,0047

m3

= 0,0035

m3

Strona 3

3. Zestawienie obciążeń.
3.1. Ustalenie wartości sił oddziaływań kół suwnicy.
3.1.1. Obciążenia pionowe.
maksymalny nacisk koła suwnicy od udźwigu:

= 94,23

kN

maksymalny nacisk koła suwnicy od ciężaru własnego:

= 91,77

kN

minimalny nacisk koła suwnicy

= -72,35

kN

minimalny nacisk koła suwnicy od udźwigu

= 5,77

kN

minimalny nacisk koła suwnicy od ciężaru własnego:

= -78,12

kN

wartość obciążeń pionowych na belkę

β

=

1,2

a) charakterystyczne

= 223,20

kN

dla stanu granicznego użytkowania

= -86,82

kN

b) obliczeniowe

γ

f

=

1,1

= 245,52

kN

dla stanu granicznego nośności

= -95,50

kN

3.1.2. Obciążenia poziome równoległe do toru jazdy.
a) charakterystyczne

= 22,32

kN

= -8,68

kN

b) obliczeniowe

γ

f

=

1,1

= 24,55

kN

-9,55

kN

3.1.3. Obciążenia poziome prostopadłe do toru jazdy.
a) charakterystyczne

k

=

0,21

= 39,06

kN

-8,68

kN

b) obliczeniowe

γ

f

=

1,1

= 42,97

kN

= -9,55

kN

3.2. Obciążenia stałe:
szyna typ: SD75

g

ks

=

0,565

kN/m

=

0,622

kN/m

belka podsuwnicowa (środnik, pas górny, pas dolny)

g

kb,sr

= 1,458

kN/m

g

kb,pg

= 0,660

kN/m

g

kb,pd

= 0,471

kN/m

= 2,589

kN/m

= 2,848

kN/m

blacha żeberkowa

g

kz

= 0,479

kN/m

= 0,527

kN/m

ceownik C180

g

kce

= 0,220

kN/m

= 0,242

kN/m

łączniki i żeberka

g

k1

= 0,120

kN/m

= 0,132

kN/m

Strona 4

ŁĄCZNIE
Obciążenie przypadające na:
a) belkę podsuwnicową:

= 3,514

kN/m

= 3,865

kN/m

b) na tężnik podłużny:

= 0,460

kN/m

= 0,505

kN/m

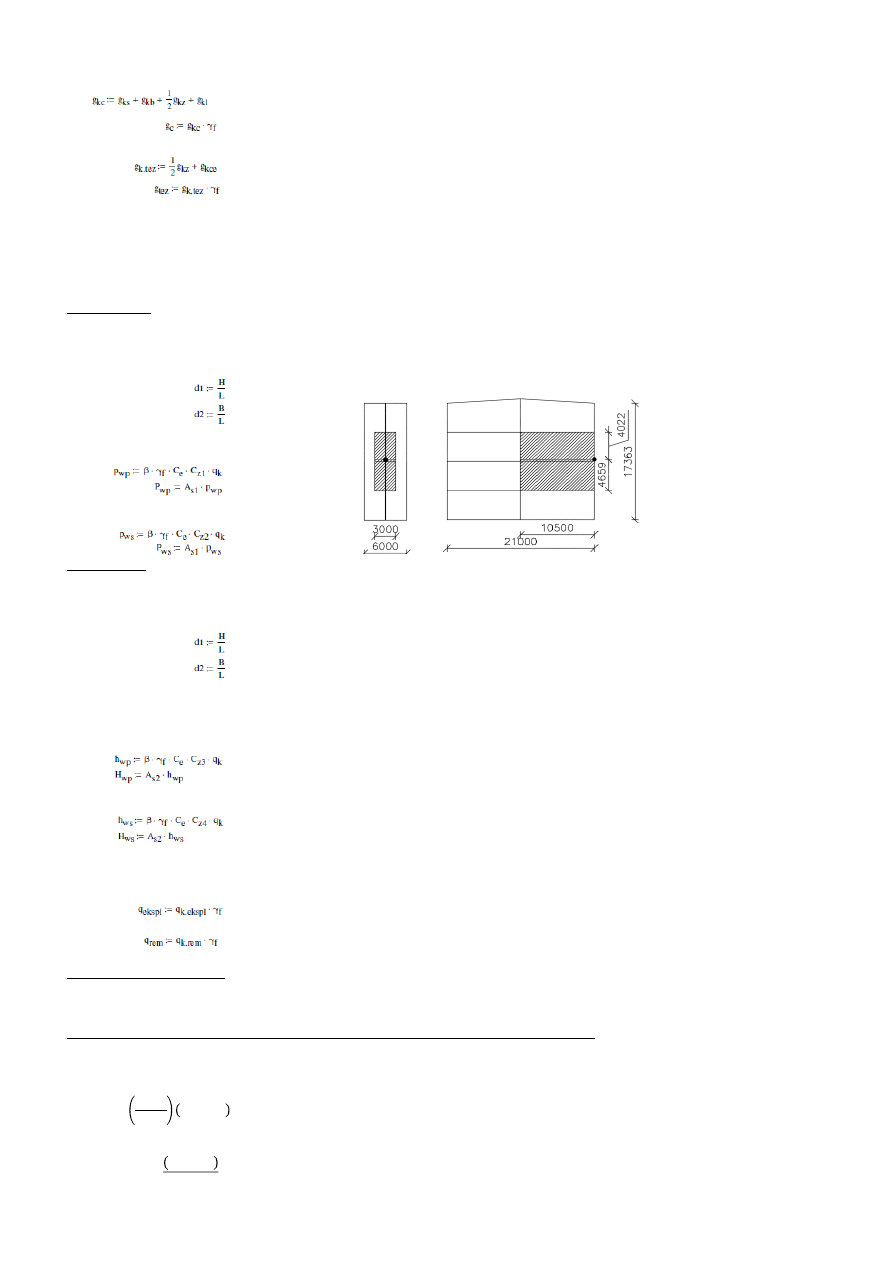
3.3. Obciążenie wiatrem.
Lokalizacja hali: Pszczyna - I strefa wiatrowa
Współczynnik działania porywów wiatru:

β

= 1,8

Współczynnik ekspozycji:

C

e

= 1

teren kategorii A

Ciśnienie prędkości wiatru:

q

k

= 0,3

kN/m2

Współczynnik obciążenia:

γ

f

= 1,5

*ściana szczytowa
Dane:

H

= 18,00

m

wysokość hali

B

= 150,00

m

długość hali

L

= 21,00

m

szerokość hali

= 0,857

= 7,14

As1

= 91,61

m2

Parcie:

C

z1

= 0,7

=

0,567

kN/m2

=

51,94

kN

Ssanie:

C

z2

= -0,3
= -0,243

kN/m2

= -22,262

kN

*ściana podłużna
Dane:

H

= 18,00

m

wysokość hali

L

= 150,00

m

długość hali

B

= 21,00

m

szerokość hali

= 0,120

= 0,140

As2

= 44,04

m2

Parcie:

C

z3

= 0,7

= 0,567

kN/m2

= 24,971

kN

Ssanie:

C

z4

= -0,4
= -0,324

kN/m2

= -14,269

kN

3.4. Obciążenie pomostu belki:

q

k.ekspl

= 1,50

kN/m2

γ

f

= 1,4

= 2,10

kN/m2

q

k.rem

= 2,50

kN/m2

γ

f

= 1,3

= 3,25

kN/m2

4. Obliczanie sił przekrojowych.
4.1. Siły przekrojowe w belce podsuwnicowej.
4.1.1. Siły wewnętrzne od oddziaływania kół suwnicy.
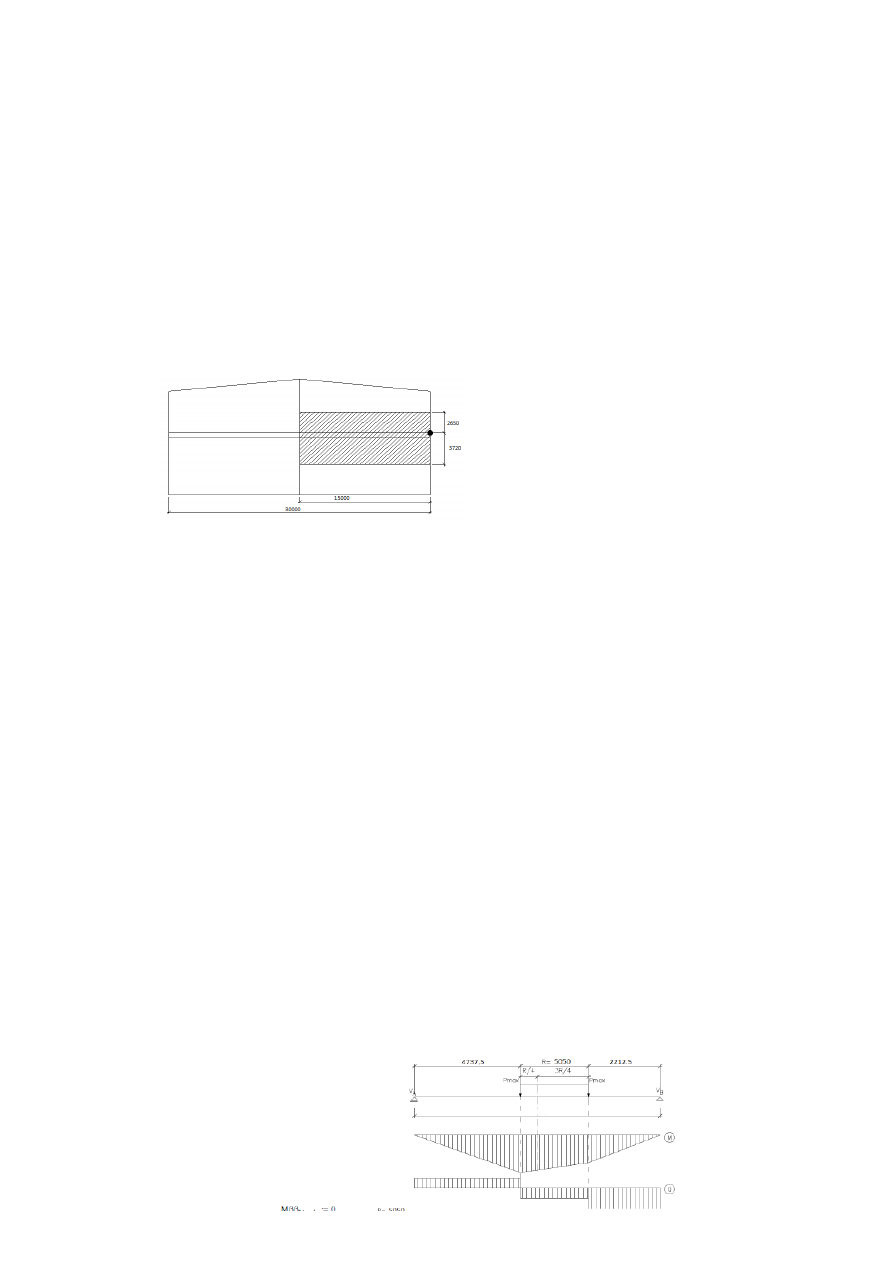
* przekrój maksymalnego momentu zginającego : α-α
Jeżeli R≥ 0,5857*L

bp

to największy moment zginający uzyskuje się przy ustawieniu koła suwnicy na środku belki.

L

bp

= 6

m

R

= 5,00

m

>

=

3,5142 m

V

max

= 245,520

kN

= 250,635

kN

Mαα

V.max

= M

Pmax

maksymalny moment zginający w przekroju

= 143,220

kN

V

αα

Vodp

=

Q

APmax

odpowiadająca siła poprzeczna

𝑄

𝐴𝑃𝑚𝑎𝑥

= 𝑉

𝑚𝑎𝑥

2𝐿

𝑏𝑝

− 𝑅

2𝐿

𝑏𝑝

𝑀

𝑃𝑚𝑎𝑥

=

𝑉

𝑚𝑎𝑥

8 ∙ 𝐿

𝑏𝑝

2𝐿

𝑏𝑝

− 𝑅

2

0,5857 ∙ 𝐿

𝑏𝑝

Strona 5

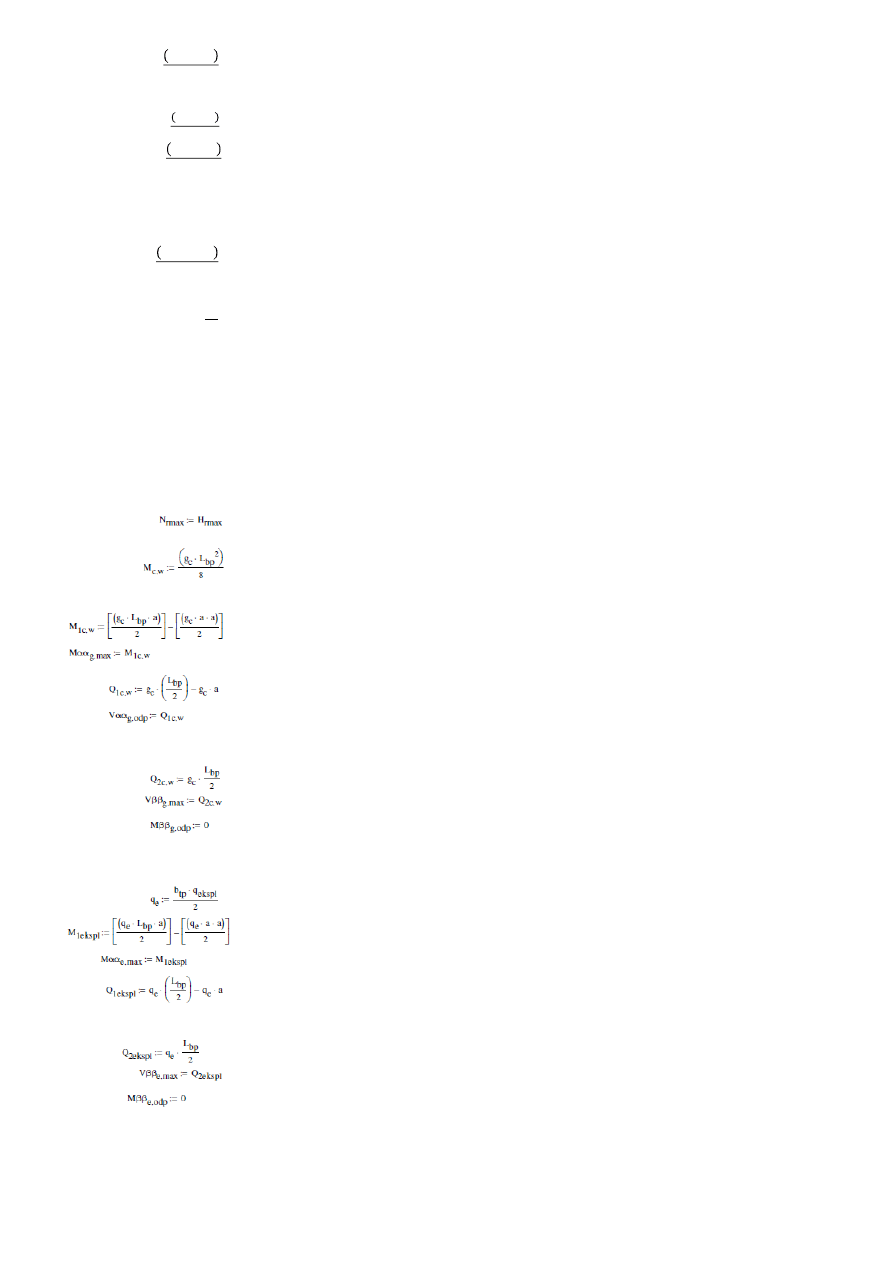
= 347,820

kN

* przekrój maksymalnej siły poprzecznej: β-β

= 204,600

kN

= 286,440

kN

Vββ

Vmax

= Q

APmax

Mββ

V.odp

= 0

kNm

* moment od oddziaływania sił poziomych, prostopadłych do belki H

p

a) przekrój α-α

a

= 3

m

= 64,449

kN

Mαα

Hpmax

= M

1Hp

= 21,483

kN

Vαα

Hpodp

= V

1HpA

= 21,483

kN

b) przekrój β-β

= 42,966

kN

Vββ

Hpmax

= V

2HpA

Mββ

Hpmax

= 0

* siła od oddziaływań równoległych do belki H

r

= 24,552

kN

= 17,392

kNm

a) przekrój α-α

a = 3

m

= 17,392

kNm

= 0,000

kN

b) przekrój β-β

= 11,595

Kn

4.1.3. Siły wewnętrzne od obciążenia użytkowego.
a) przekrój α-α

a = 3

m

= 0,84

kN/m

= 3,780

kNm

= 0,000

kN

b) przekrój β-β

= 2,52

kN

𝑄

𝐵𝑃𝑚𝑎𝑥

=

𝑉

𝑚𝑎𝑥

∙ 𝑅

𝐿

𝑏𝑝

𝑄

𝐴𝑃𝑚𝑎𝑥

= 𝑉

𝑚𝑎𝑥

2𝐿

𝑏𝑝

− 𝑅

𝐿

𝑏𝑝

𝑄

𝐵𝑃𝑚𝑎𝑥

= 𝑉

𝑚𝑎𝑥

2𝐿

𝑏𝑝

+ 𝑅

2𝐿

𝑏𝑝

𝑀

1𝐻𝑝

=

𝐻

𝑝𝑚𝑎𝑥

∙ 𝑎

2

2𝑎

𝑉

1𝐻𝑝𝐴

= 𝐻

𝑝𝑚𝑎𝑥

𝑎

2𝑎

𝑉

1𝐻𝑝𝐵

= 𝑉

1𝐻𝑝𝐴

𝑉

2𝐻𝑝𝐴

= 𝐻

𝑝𝑚𝑎𝑥

Strona 6

4.1.4. Siły wewnętrzne od obciążenia remontowego.
a) przekrój α-α

a = 3

m

= 1,300

kN/m

= 5,850

kNm

Mαα

rmax

=

M

1rem

= 0,000

kN

Vαα

rodp

=

Q

1rem

b) przekrój β-β

= 3,900

kN

Vββ

rmax

=

Q

1rem

Mββ

rodp

=

0

4.1.5. Siły wewnętrzne od parcia i ssania wiatru.
*od działania wiatru na ścianę szczytową

= 51,944

kN

= -22,262

kN

* od działania wiatru na ścianę podłużną- parcie
a) przekrój α-α

H

wp

=

24,971

kN

= 37,456

kNm

= 12,485

kN

b) przekrój β-β

= 12,485

kN

* od działania wiatru na ścianę podłużną- ssanie
a) przekrój α-α

H

ws

=

-14,269

kN

= -21,403

kNm

= -7,134

kN

b) przekrój β-β

= -7,134

kN

4.2. Obliczanie sił przekrojowych w tężniku podłużnym.
4.2.1. Ciężar własny.

γ

f

=

1,1

g

k.tez

= 0,460

kN/m

= 0,505

kN/m

* wartości obliczeniowe

= 2,275

kNm

= 1,895

kN

* wartości charakterystyczne

= 2,068

kN

= 1,723

kN

𝑄

1𝑟𝑒𝑚

= 𝑞

𝑟

𝐿

𝑏𝑝

2

𝑄

1𝑟𝑒𝑚

= 𝑞

𝑟

𝐿

𝑏𝑝

2

− 𝑞

𝑟

∙ 𝑎

𝑔

𝑡𝑒𝑧

= 𝑔

𝑘𝑡𝑒𝑧

∙ 𝛾

𝑓

Strona 7

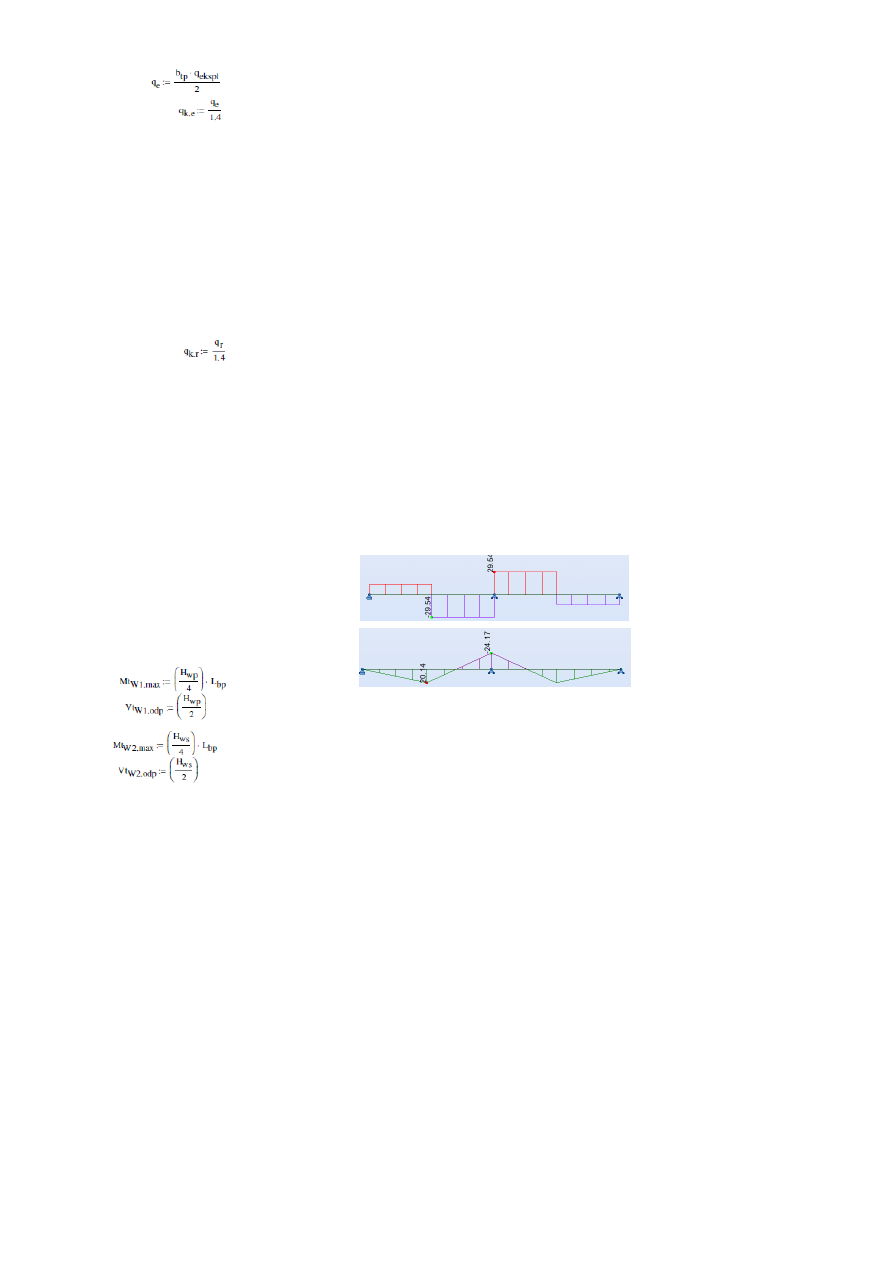
4.2.2. Obciążenie użytkowe.

= 0,84

kN/m

= 0,600

kN/m

*wartości obliczeniowe

= 3,780

kNm

= 3,150

kN

*wartości charakterystyczne

= 2,700

kNm

= 2,250

kN

4.2.3. Obciążenie remontowe.

q

r

= 1,300

kN

= 0,929

kN/m

* wartości obliczeniowe

= 5,850

kNm

= 4,875

kN

* wartości charakterystyczne

= 2,700

kNm

= 2,250

kN

4.2.4. Oddziaływanie kół suwnicy prostopadle do tężnika.
Siły przekrojowe w środku rozpiętości tężnika wyznaczono w programie do obliczeń statycznych

H

pmax

= 42,966

kN

* wartości obliczeniowe

Mt

Hp.max

= 22,154

kNm

Vt

Hp.odp

= 32,494

kN

* wartości charakterystyczne

Mt

kHp.max

= 20,140

kNm

Vt

kHp.odp

= 29,540

kN

4.2.5. Obciążenie wiatrem.
*parcie

= 37,456

kNm

= 12,485

kN

*ssanie

= -21,403

kNm

= -7,134

kN

4.3. Zestawienie wyników dla belki podsuwnicowej.
* maksymalne oddziaływanie od kół suwnicy

Mαα

V.max

= 250,635

kNm

Vαα

V.odp

= 143,220

kN

Mββ

V.odp

= 0

kNm

Vββ

V.max

= 286,440

kN

* ciężar własny belki

Mαα

g.max

= 17,392

kNm

Vαα

g.odp

= 0,000

kN

Mββ

g.odp

= 0

kNm

Vββ

g.max

= 11,595

kN

𝑉𝑡

𝑟.𝑜𝑑𝑝

= 0,625 ∙ 𝑞

𝑟

∙ 𝐿

𝑏𝑝

𝑀

𝑘𝑟

= 0,125 ∙ 𝑞

𝑘𝑒

∙ 𝐿

𝑏𝑝

2

𝑉𝑡

𝑘𝑟𝑜𝑑𝑝

= 0,625 ∙ 𝑞

𝑘𝑒

∙ 𝐿

𝑏𝑝

𝑀

𝑡𝑟𝑚𝑎𝑥

= 0,125 ∙ 𝑞

𝑟

∙ 𝐿

𝑏𝑝

2

𝑀𝑘

𝑒𝑟𝑚𝑎𝑥

= 0,125 ∙ 𝑞

𝑘𝑒

∙ 𝐿

𝑏𝑝

2

𝑉𝑘

𝑒𝑜𝑑𝑝

= 0,625 ∙ 𝑞

𝑘𝑒

∙ 𝐿

𝑏𝑝

𝑀𝑡

𝑒𝑚𝑎𝑥

= 0,125 ∙ 𝑞

𝑒

∙ 𝐿

𝑏𝑝

2

𝑉𝑡

𝑒𝑜𝑑𝑝

= 0,625 ∙ 𝑞

𝑒

∙ 𝐿

𝑏𝑝

Strona 8

* oddziaływanie eksploatacyjne

Mαα

e.max

= 3,780

kNm

Vαα

e.odp

= 0,000

kN

Mββ

e.odp

= 0

kNm

Vββ

e.max

= 2,520

kN

* oddziaływania remontowe

Mαα

r.max

= 5,850

kNm

Vαα

r.odp

= 0,000

kN

Mββ

r.odp

= 0

kNm

Vββ

r.max

= 3,900

kN

*oddziaływania prostopadłe do belki /H

p

/

Mαα

Hp.max

= 64,449

kNm

Vαα

Hp.odp

= 21,483

kN

Mββ

Hp.odp

= 0

kNm

Vββ

Hp.max

= 42,966

kN

* oddziaływanie wiatru (1)

Mαα

W1.max

= 37,456

kNm

Vαα

W1.odp

= 12,485

kN

Mββ

W1.odp

= 0

kNm

Vββ

W1.max

= 12,485

kN

* oddziaływanie wiatru (2)

Mαα

W2.max

= -21,403

kNm

Vαα

W2.odp

= -7,134

kN

Mββ

W2.odp

= 0

kNm

Vββ

W2.max

= -7,134

kN

* oddziaływanie wiatru na ścianę szczytową (2)

N

c1

= 51,944

kN

N

t1

= -22,262

kN

* oddziaływanie równoległe do toru jazdy

H

rmax

= 24,552

kN

4.4. Zestawienie wyników dla tężnika hamownego.
*ciężar własny

Mt

g.max

= 2,275

kNm

Vt

g.odp

= 1,895

kN

* oddziaływanie użytkowe

Mt

e.max

= 3,780

kNm

Vt

e.odp

= 3,150

kN

* oddziaływanie remontowe

Mt

r.max

= 5,850

kNm

Vt

r.odp

= 4,875

kN

* oddziaływanie prostopadłe

Mt

Hp.max

= 22,154

kNm

Vt

Hp.odp

= 32,494

kN

* oddziaływanie wiatru (1)

Mt

W1.max

= 37,456

kNm

Vt

W1.odp

= 12,485

kN

* oddziaływanie wiatru (2)

Mt

W2.max

= -21,403

kNm

Vt

W2.odp

= -7,134

kN

Strona 9

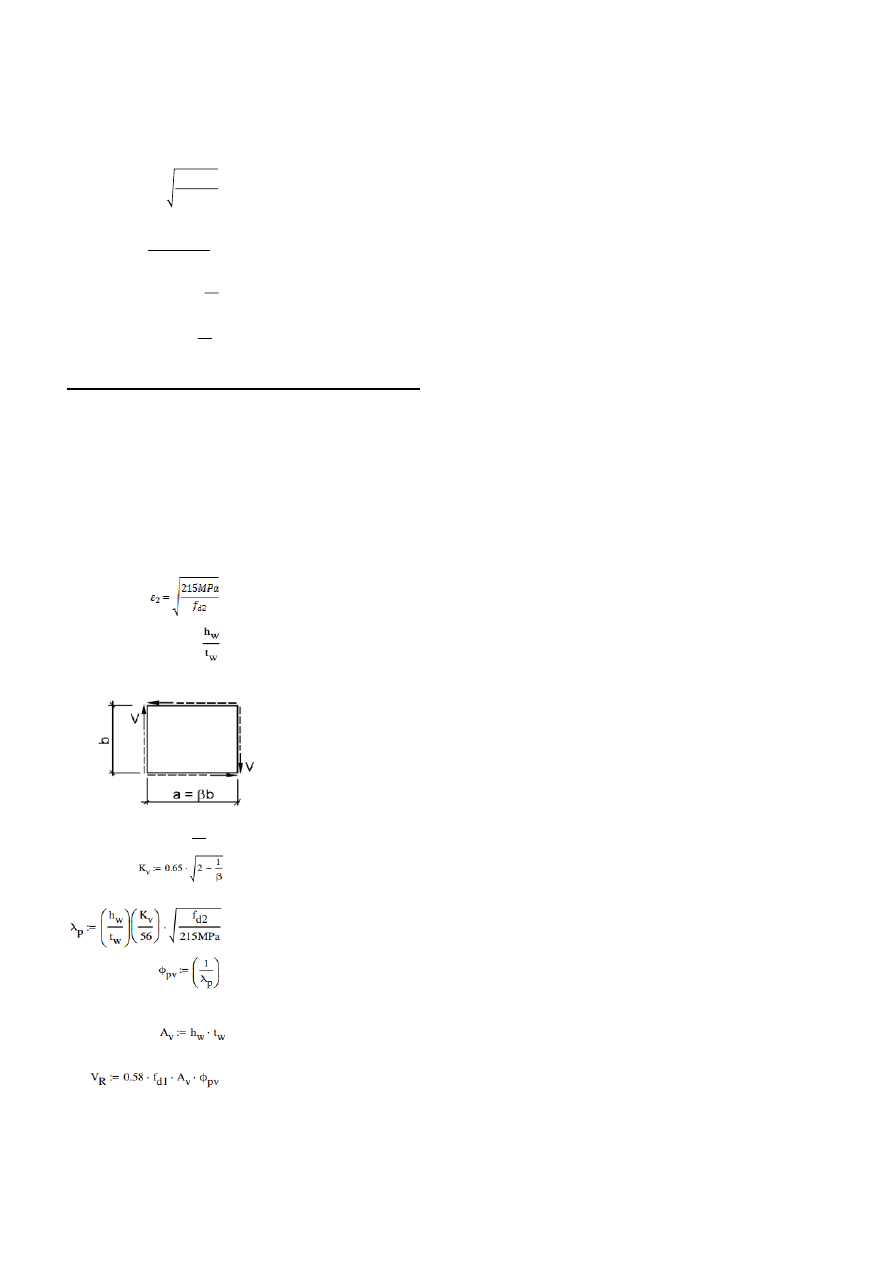
4.5. Sprawdzenie klasy przekroju:

f

d

= 295

MPa

t

g

= 20

mm

t

f

= 20

mm

t

w

= 16

mm

b

g

= 420

mm

b

d

= 300

mm

h

w

= 560

mm

= 0,854

* zginanie
a) pas górny

= 10,100

<

14ε = 11,951881

Przekrój klasy 3

b) środnik

= 35,000

<

105ε = 89,639107

Przekrój klasy 3

*scinanie

= 35,000

<

70ε = 59,759405

Przekrój klasy 3

5. Sprawdzenie warunków nośności (stateczności) belki podsuwnicowej.
5.1. Sprawdzenie ścinania.
5.1.1. Przekrój podporowy.
Maksymalna siła poprzeczna w przekroju:

ψ

1

= 1

ψ

2

= 0,9

=

300,30

kN

Sprawdzenie klasy przekroju przy ścinaniu

h

w

= 0,560

m

t

w

= 0,016

m

t

g

= 20

mm

f

d2

= 295

MPa

= 0,854

Przekrój klasy 3

= 35,0

<

=

59,759

Obliczanie współczynnika niestateczności przy ścinaniu φ

pv

schemat podparcia i obciążenia ścianki

= 5,357

>

1

= 0,875

>

0,8

przyjęto K

v

=0,8

Smukłość wględna ścianki:

= 0,586

= 1,707

Sprawdzenie nośności na ścinanie:

= 0,009

m2

pole przekroju czynnego

Nośność obliczeniowa przy ścinaniu:

= 2706,3

kN

Vββ

= 300,303

kN

<

V

R

= 2706,3

kN

warunek nośności został spełniony

5.1.2. Przekrój przęsłowy.
Maksymalna siła poprzeczna w przekroju:

ψ

1

= 1

ψ

2

= 0,9

=

143,220

kN

70 ∙ 𝜀

2

𝑉𝛽𝛽 = 𝑉𝛽𝛽

𝑔.𝑚𝑎𝑥

+ 𝜓

1

∙ 𝑉𝛽𝛽

𝑉.𝑚𝑎𝑥

+ 𝜓

2

∙ 𝑉𝛽𝛽

𝑒.𝑚𝑎𝑥

𝑉𝛼𝛼 = 𝑉𝛼𝛼

𝑔.𝑜𝑑𝑝

+ 𝜓

1

∙ 𝑉𝛼𝛼

𝑉.𝑜𝑑𝑝

+ 𝜓

2

∙ 𝑉𝛼𝛼

𝑒.𝑜𝑑𝑝

𝜀 =

215𝑀𝑃𝑎

𝑓

𝑑

0,5(𝑏

𝑔

− 𝑡

𝑤

)

𝑡

𝑔

ℎ

𝑤

𝑡

𝑤

ℎ

𝑤

𝑡

𝑤

𝛽 =

𝑎

ℎ

𝑤

Strona 10

Sprawdzenie nośości na ścinanie:

V

0

=0,3*V

R

= 811,886

kN

Vαα

= 143,220

kN

<

V

0

= 811,886

kN

warunek został spełniony

5.1.3. Tężnik podłużny ( przekrój nad podporą).

ψ

1

= 1

ψ

2

= 0,9
= 6,770

kN

Sprawdzenie stateczności na ścinanie:

= 180

mm

f

d1

=

305

= 8

mm

= 11

mm

= 0,158

m

= 0,001264

m2

pole przekroje czynnego

= 0,840

=

19,75

<

= 58,771578

ścianka jest odporna na miejscową utratę stateczności

= 1

Sprawdzenie nośności na ścinanie:

= 0,010

m2

pole przekroju czynnego

Nośność obliczeniowa przy ścinaniu:

= 223,602

kN

= 6,770

kN

<

= 223,602

kN

warunek nośności został spełniony

5.2. Sprawdzenie naprężeń normalnych.
Wartości sił przekrojowych w belce podsuwnicowej od:
ODDZIAŁYWAŃ PIONOWYCH
*ciężaru własnego:

M

αα

g.max

= 17,392

kNm

V

αα

g.odp

= 0,000

kN

*pionowego oddziaływania kół suwnicy:

M

αα

V

.max

= 250,635

kNm

V

αα

V.odp

= 143,220

kN

* obciążenia eksploatacyjnego:

M

αα

e.max

= 3,780

kNm

V

αα

e.odp

= 0,000

kN

* obciążenia remontowego:

M

αα

r.max

= 5,850

kNm

V

αα

r.odp

= 0,000

kN

ODDZIAŁYWAŃ POZIOMYCH PROSTOPADŁYCH DO TORU SUWNICY
* poziomego oddziaływania kół suwnicy:

M

αα

Hp.max

= 64,449

kNm

* obciążenia wiatrem:

M

αα

W2.max

= -21,403

kNm

ODDZIAŁYWAŃ POZIOMYCH RÓWNOLEGŁYCH DO TORU SUWNICY
* obciążenia wiatrem:

N

c1

= 51,944

kN

* poziomego oddziaływania kół suwnicy (rówoległe do toru)

H

rmax

= 24,552

kN

Wartości sił przekrojowych w tężniku podłużnym od:
ODDZIAŁYWAŃ PIONOWYCH
*ciężaru własnego:

M

t

g.max

= 2,275

kNm

V

t

g.odp

= 1,895

kN

* obciążenia eksploatacyjnego:

M

t

e.max

= 3,780

kNm

V

t

e.odp

= 3,150

kN

* obciążenia remontowego:

M

t

r.max

= 5,850

kNm

V

t

r.odp

= 4,875

kN

ODDZIAŁYWAŃ POZIOMYCH
* poziomego oddziaływania kół suwnicy:

M

t

Hp.max

= 22,154

kNm

V

t

Hp.odp

= 32,494

kN

* obciążenia wiatrem:

M

t

W1.max

= 37,456

kNm

V

t

W1.odp

= 12,485

kN

M

t

W2.max

= -21,403

kNm

ℎ

𝐶180

𝑡

𝑤𝐶180

𝑡

𝑓𝐶180

ℎ

𝑤𝐶180

= ℎ

𝐶180

− 2 ∙ 𝑡

𝑓𝐶180

𝐴

𝑣1

= ℎ

𝑤𝐶180

∙ 𝑡

𝑤𝐶180

ℎ

𝑤𝐶180

𝑡

𝑤𝐶180

70 ∙ 𝜀

1

𝜑

𝑝𝑣

𝐴

𝑣

= ℎ

𝑤

∙ 𝑡

𝑤

𝑉

𝑥𝑡

= 𝑉𝑡

𝑔.𝑜𝑑𝑝

+ 𝜓

1

∙ 𝑉𝑡

𝑟.𝑜𝑑𝑝

𝜀

1

=

215𝑀𝑃𝑎

𝑓

𝑑1

𝑉

𝑅1

= 0,58 ∙ 𝑓

𝑑1

∙ 𝐴

𝑉1

∙ 𝜑

𝑝𝑣

𝑉

𝑥𝑡

𝑉

𝑅1

Strona 11

V

t

W2.odp

= -7,134

kN

5.2.1. Sprawdzenie naprężeń w pasie dolnym belki podsuwnicowej

W

x2

= 0,004

m3

Wartości współczynników jednoczesności obciążeń zmiennych wg [N2]:

ψ

1

= 1

ψ

2

= 0,9

=

68,2777 MPa

< f

d2

=

295 MPa

warunek nośności został spełniony

5.2.2. Sprawdzenie naprężeń w pasie górnym belki podsuwnicowej.
Pole przekroju zastępczego:

= 0,012

m2

ψ

1

= 1

ψ

2

= 0,9

ψ

3

= 0,8

ψ

4

= 0,7

=

143,220

kN

= 143,220

kN

<

=

811,886 kN

a) oddziaływania od obciążeń ciężarem własnym, pionowym i poziomym od suwnicy
( prostopadłym do toru) obciążenia eksploatacyjnego i wiatru) ssanie na ścianę boczną i parcie na szczytową):

ψ

1

= 1

ψ

2

= 0,9

ψ

3

= 0,8

ψ

4

= 0,7

=

= 75,201

MPa

<

f

d2

=

295 MPa

warunek nośności został spełniony

b) oddziaływania od obciążeń ciężarem własnym, pionowym i poziomym od suwnicy
(równoległym do toru) obciążenia eksploatacyjnego i wiatru (ssanie na ścianę boczną i parcie na szczytową)

=

= 64,637

MPa

<

f

d2

=

295 MPa

warunek nośności został spełniony

c) oddziaływania od obciążenia ciężarem własnym, remontowego, pionowego od suwnicy i wiatrem
(ssanie na ścianę boczną i szczytową)

=

62,832

MPa

= 62,832

MPa

<

f

d2

=

295 MPa

5.2.3. Sprawdzenie naprężeń na krawędzi pasa tężnika:
Warunek (p.4.5.2.d normy [N1]) dla oddziaływań pionowych:
Wartość współczynników jednoczesności obciążeń zmiennych wg normy [N2]:

ψ

1

= 1

ψ

2

= 0,9

ψ

3

= 0,8

ψ

4

= 0,7
= 6,770

kN

<

=

223,602 kN

warunek został spełniony

Warunek (p.4.5.2.d normy [N1]) dla oddziaływań poziomych

= 26,073

kN

= 11,000

mm

= 180,000

mm

= 0,00396

m2

= 1

ścianka jest odporna na miejscową utratę stateczności

= 677,556

kN

= 203,267

kN

= 26,073

kN

<

=

203,267 kN

Sprawdzenie warunków nośności:

= 0,00015

m3

= 0,003

m3

=

47,180633 MPa

a) oddziaływania od obciążeń ciężarem własnym, poziomym suwnicy (prostopadłym do toru), obciążenia eksploatacyjnego i
wiatru (ssanie na ścianę boczną):

𝜎

2

=

𝑀𝛼𝛼

𝑔.𝑚𝑎𝑥

𝑊

𝑥2

+ 𝜓

1

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

𝑊

𝑥2

+ 𝜓

2

𝑀𝛼𝛼

𝑒..𝑚𝑎𝑥

𝑊

𝑥2

𝐴

𝑏𝑟𝑢𝑡𝑡𝑜

= 𝑡

𝑓𝑔

∙ 𝑏

𝑔

+ 15 ∙ 𝑡

𝑤

∙ 𝑡

𝑤

𝑉

𝑥

= 𝑉𝛼𝛼

𝑔.𝑜𝑑𝑝

+ 𝜓

1

∙ 𝑉𝛼𝛼

𝑉.𝑜𝑑𝑝

+ 𝜓

4

∙ 𝑉𝛼𝛼

𝑒.𝑜𝑑𝑝

𝑉

𝑥

𝑉

0

𝜎

1

=

𝑀𝛼𝛼

𝑔.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

4

𝑀𝛼𝛼

𝑒.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

1

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

2

𝑀𝛼𝛼

𝐻𝑝.𝑚𝑎𝑥

𝑊

𝑦1

+ 𝜓

3

−𝑀𝛼𝛼

𝑊2.𝑚𝑎𝑥

𝑊

𝑦1

𝜎

1

=

𝑀𝛼𝛼

𝑔.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

1

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

4

𝑀𝛼𝛼

𝑒.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

2

𝐻

𝑟.𝑚𝑎𝑥

𝐴

𝑏𝑟𝑢𝑡𝑡𝑜

+ 𝜓

3

−𝑀𝛼𝛼

𝑊2.𝑚𝑎𝑥

𝑊

𝑦1

+ 𝜓

3

𝑁

𝑐1

𝐴

𝑏𝑟𝑢𝑡𝑡𝑜

𝜎

1

=

𝑀𝛼𝛼

𝑔.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

1

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

4

𝑀𝛼𝛼

𝑟.𝑚𝑎𝑥

𝑊

𝑥1

+ 𝜓

3

−𝑀𝛼𝛼

𝑊2.𝑚𝑎𝑥

𝑊

𝑦1

𝜎

1

𝑉

𝑥𝑡

= 𝑉𝑡

𝑔.𝑜𝑑𝑝

+𝜓

1

∙ 𝑉𝑡

𝑟.𝑜𝑑𝑝

𝜎

1

𝜎

1

𝑉

𝑅1

𝑉

𝑦𝑡

= 𝜓

1

𝑉𝑡

𝐻𝑝.𝑜𝑑𝑝

+−𝜓

2

𝑉𝑡

𝑊2.𝑜𝑑𝑝

𝑡

𝑓𝐶180

𝑏

𝐶180

𝐴

𝑣𝑡

= 2 ∙ 𝑡

𝑓𝐶180

∙ 𝑏

𝐶180

𝜑

𝑝𝑣

𝑉

𝑅𝑦

= 0,58 ∙ 𝑓

𝑑2

∙ 𝐴

𝑣𝑡

∙ 𝜑

𝑝𝑣

𝑉

0𝑦

= 0,3 ∙ 𝑉

𝑅𝑦

𝑉

𝑦𝑡

𝑉

0𝑦

𝑊

𝑥𝐶180

𝑊

𝑦3

𝜎

3

=

𝑀𝑡

𝑔.𝑚𝑎𝑥

𝑊

𝑥𝐶180

+ 𝜓

3

𝑀𝑡

𝑒.𝑚𝑎𝑥

𝑊

𝑥𝐶180

+ 𝜓

1

𝑀𝑡

𝐻𝑝.𝑚𝑎𝑥

𝑊

𝑦3

+ 𝜓

2

−𝑀𝛼𝛼

𝑊2.𝑚𝑎𝑥

𝑊

𝑦3

Strona 12

= 47,181

MPa

<

f

d2

=

295,00 MPa

warunek nośności został spełniony

=

56,0143

MPa <

f

d2

=

295 MPa

warunek nośności został spełniony

5.3. Sprawdzenie warunku stateczności środnika belki podsuwnicowej w złożonym stanie naprężeń.
5.3.1. Przekrój podporowy
Siła osiowa przypadająca na środnik N

w

:

*poziome oddziaływanie kół suwnicy (równoległe do toru)

H

rmax

= 24,552

kN

* oddziaływanie wiatru na ściane szczytową (2)

N

c1

= 51,944

kN

= 71,302

kN

Pole przekroju czynnego belki podsuwnicowej:

A

g

=

0,012

m2

Pole współpracującej części przekroju (jak w stanie nadkrytycznym):

= 0,00384

m2

= 22,369

kN

= 1171,200

kN

Moment zginający przypadający na środnik M

w

M

w

= 0,000

kN

podpora

Nośność obliczeniowa środnika przy zginaniu M

Rw

Wskaźnik bezwładności belki:

= 836,267

= 255,061

kNm

Siła skupiona:

P

max

= 196,000

kN

β

= 1,300

współczynnik dynamiczny

Obliczeniowa nośność środnika obciążonego siłą skupioną

c

= 35,000

mm

d

= 95,000

mm

c

0

= 225,000

mm

przyjmuję:

c

0

= 230,000

mm

=

23,7188 >

=

14,375

= 23,719

>

=

16,792

Z uwagi na niespełnienie powyższych warunków przyjęto

k

c

=

14,06

= 5,825

MPa

<

=

152,5 MPa

= 1097,805

kN

Siła poprzeczne przypadająca na środnik V

1

V

1

= Vββ

V

1

= 300,303

kN

Nośność środnika na ścinanie V

R:

V

R

= 2706,288

kN

φ

p

= 1,0

=

0,0621152 <

1

warunek nośności został spełniony

5.3.2. Przekrój przęsłowy.
Siła osiowa przypadająca na środnik N

w

:

N

1

= 71,302

kN

A

g

= 0,012

m2

A

e

= 0,0038

m2

N

W

= 22,369

kN

Nośność obliczeniowa środnika przy ściskaniu N

Rw

Nośność obliczeniowa środnika przy ściskaniu N

Rw

(przyjmujemy jak nośność w stanie nadkrytycznym w przypadku obciążeń

statycznych i braku sił P- dlatego obliczaliśmy A

e

)

𝑦3

𝑦3

𝜎

3

𝜎

3

=

𝑀𝑡

𝑔.𝑚𝑎𝑥

𝑊

𝑥𝐶180

+ 𝜓

3

𝑀𝑡

𝑟.𝑚𝑎𝑥

𝑊

𝑥𝐶180

+ 𝜓

2

𝑀𝛼𝛼

𝑊1.𝑚𝑎𝑥

𝑊

𝑦3

𝑁

1

= 𝜓

1

∙ 𝐻

𝑟𝑚𝑎𝑥

+ 𝜓

2

∙ 𝑁

𝑐1

𝐴

𝑒

= 15 ∙ 𝑡

𝑤

∙ 𝑡

𝑤

𝑁

𝑤

=

𝐴

𝑒

𝐴

𝑔

∙ 𝑁

1

𝑁

𝑅𝑤

= 𝐴

𝑒

∙ 𝑓

𝑑1

𝑊

𝑒

=

(𝑡

𝑤

∙ ℎ

𝑤

2

)

6

𝑀

𝑅𝑤

= 𝑊

𝑒

∙ 𝑓

𝑑1

𝑘

𝑐

= 15 + 25 ∙

𝑐

0

ℎ

𝑤

215𝑀𝑃𝑎

𝑓

𝑑1

∙

𝑡

𝑓

𝑡

𝑤

𝑐

0

𝑡

𝑤

𝑘

𝑐

20 ∙

215𝑀𝑃𝑎

𝑓

𝑑1

𝜎

𝑐

=

𝑁

𝑤

𝐴

𝑒

0,5 ∙ 𝑓

𝑑1

𝑃

𝑅𝑐

= 𝑘

𝑐

∙ 𝑡

𝑤

2

∙ 𝑓

𝑑1

𝑁

𝑤

𝑁

𝑅𝑤

+

𝑀

𝑤

𝑀

𝑅𝑤

+

𝛽 ∙ 𝑃

𝑚𝑎𝑥

𝑃

𝑅𝑐

2

− 3𝜙

𝑝

∙

𝑀

𝑤

𝑀

𝑅𝑤

+

𝑁

𝑤

𝑁

𝑅𝑤

𝛽 ∙ 𝑃

𝑚𝑎𝑥

𝑃

𝑅𝑐

+

𝑉

1

𝑉

𝑅

2

Strona 13

N

Rw

= 1171,200

kN

Moment zginający przypadający na środnik M

w:

Moment od oddziaływań pionowych:
*ciężaru własnego:

M

αα

g.max

= 17,392

kNm

* pionowego oddziaływania kół suwnicy:

M

αα

V.max

= 250,635

kNm

* obciążenia eksploaacyjnego:

M

αα

e.max

= 3,780

kNm

=

270,673

kNm

Nośność obliczeniowa środnika przy zginaniu M

Rw

M

Rw

= 255,061

kNm

Siła skupiona:

P

max

= 186,000

kNm

β

= 1,300

współczynnik dynamiczny

Obliczeniowa nośność środnika obciążonego siłą skupioną

c

0

= 230,000

mm

k

c

=

14,06

Odległość ściskanej krawędzi środnika do osi obojętnej:

= 0,330

m

= 73,913

Mpa

<

=

152,5 MPa

= 1097,805

kN

Siła poprzeczna przypadająca na środnik V

2

V

2

= V

x

V

2

= 143,220

kN

Nośność środnika na ścinanie V

R:

V

R

= 2706,288

kN

φ

p

= 1,0

=

0,9804298 <

1

warunek nośności został spełniony

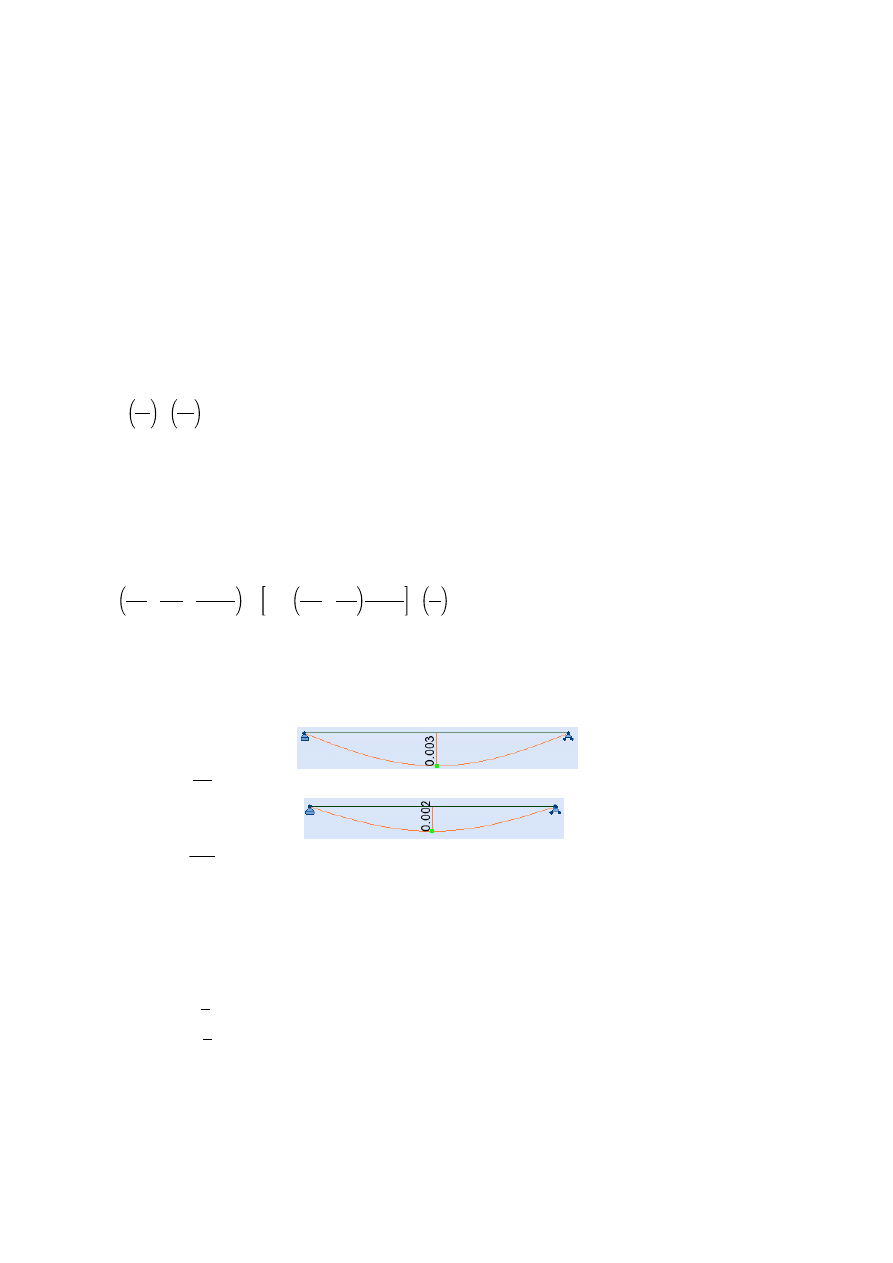
6. Sprawdzenie ugięć.

Moduł sprężystości:

E

= 205

GPa

L

bp

= 6

m

= 0,012

m

>

u

pion

=

0,003 m

= 0,006

m

>

u

poziom

=

0,002 m

7. Sprawdzenie nośności ze względu na zmęczenie belki podsuwnicowej.
Charakterystyka belki podsuwnicowej:

I

x

= 0,001

m4

W

x1

= 0,005

m3

W

x1

= 0,004

m3

Moment statyczny pasa górnego i dolnego:

= 0,002186

m3

= 0,001919

m3

Siły wewnętrzne od pionowych nacisków kół P

max

M

αα

V.max

= 250,635

kNm

Vαα

V.odp

= 143,220

kN

Vββ

V.max

= 286,440

kN

Ustalenie grupy natężenia pracy belki B
Przyjęto

grupę B5

współczynnik K=K

b

Ugięcie belki podsuwnicowej sprawdzamy wprowadzając do programu do obliczeń statycznych odpowiednie wartości
charakterystyczne obciążeń lub przy pomocy wzorów z tablic stalowych.

𝑀

𝑤

= 𝑀𝛼𝛼

𝑔.𝑚𝑎𝑥

+ 𝜓

1

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

+ 𝜓

4

𝑀𝛼𝛼

𝑒.𝑚𝑎𝑥

𝑦

𝑐

= ℎ

𝑏𝑝

− 𝑒 − 𝑡

𝑓

𝜎

𝑐

=

𝑁

𝑤

𝐴

𝑒

+

𝑀

𝑤

𝐼

𝑥

∙ 𝛾

𝑐

0,5 ∙ 𝑓

𝑑1

𝑃

𝑅𝑐

= 𝑘

𝑐

∙ 𝑡

𝑤

2

∙ 𝑓

𝑑1

𝑁

𝑤

𝑁

𝑅𝑤

+

𝑀

𝑤

𝑀

𝑅𝑤

+

𝛽 ∙ 𝑃

𝑚𝑎𝑥

𝑃

𝑅𝑐

2

− 3𝜙

𝑝

∙

𝑀

𝑤

𝑀

𝑅𝑤

+

𝑁

𝑤

𝑁

𝑅𝑤

𝛽 ∙ 𝑃

𝑚𝑎𝑥

𝑃

𝑅𝑐

+

𝑉

2

𝑉

𝑅

2

𝑢

𝑑𝑜𝑝.𝑝𝑖𝑜𝑛

=

𝐿𝑏𝑝
500

𝑢

𝑑𝑜𝑝.𝑝𝑜𝑧𝑖𝑜𝑚

=

𝐿𝑏𝑝

1000

𝑆

𝑥𝑔

= 𝑡

𝑓

∙ 𝑏

𝑔

∙ (e +

𝑡

𝑓

2

)

𝑆

𝑥𝑑

= 𝑡

𝑓

∙ 𝑏

𝑑

∙ (ℎ

𝑤

− e +

𝑡

𝑓

2

)

Strona 14

współczynnik niejednorodności widna naprężeń

α

k

K

= 1,000

m

= 3,000

= 1,000

Ustalenie grupy klasyfikacyjnej belki:
H3

maksymalna liczba cykli:

N

=

125000

7.1. Sprawdzenie pasa gónego w strefie poprzecznego żebra usztywniającego.
a) Równoważny zakres zmienności naprężeń:

= 51,655

MPa

Naprężenia ściskające:

= 30,993

MPa

= 30,993

MPa

b) Wytrzymałość zmęczeniowa:
Kategoria zmęczeniowa dla karbu w strefie żebra poprzecznego

= 80,000

MPa

= 201,093

MPa

c) warunek nośności zmęczeniowej:

γ

fat

= 1,000
= 30,993

MPa

<

=

201,09317 MPa

7.2. Spoiny pachwinowe łączące pas górny ze środnikiem.
a) Wpływ naprężeń równoległych do osi podłużnej spoiny

a

= 4

= 59,692

MPa

= 80,000

MPa

= 139,288

MPa

= 59,692

MPa

<

=

139,28809 MPa

b) Wpływ naprężeń na docisku koła suwnicy

c

0

= 225

mm

długość strefy docisku

a

= 4

mm

grubość spoiny

β

= 1,2

= 124,000

MPa

naprężenie docisku

= 74,400
= 74,400

MPa

= 45,000

MPa

Miarodajna liczba cykli:

N

m

= 250000,000

= 26,252

MPa

= 74,400

MPa

>

=

26,251645 MPa

Zmiana typu i grubości spoiny- ponowna prowadzenie obliczeń

c

0

= 225

mm

długość strefy docisku

a

= 10

mm

grubość spoiny, spoina czołowa

β

= 1,2

= 49,600

MPa

naprężenia docisku

= 29,760

MPa

= 29,760

MPa

= 57,000

MPa

Miarodajna liczba cykli:

N

m

= 250000,000

= 33,252

MPa

zakres zmienności naprężeń przy uwzględnieniu redukcji

40%

Określenie kategorii zmęczeniowej dla styku pasa ze środnikiem w elementach obciążonych siłą skupioną przy obustronnych
spoinach pachwinowych obrobionych

Określenie kategorii zmęczeniowej dla styku pasa ze środnikiem w elementach obciążonych siłą skupioną przy spoinie czołowej
K normalnej jakości

zakres zmienności naprężeń przy uwzględnieniu redukcji

40%

𝛼

𝑘

= 𝐾

1

𝑚

𝜎

𝑥

=

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

𝑊

𝑥1

𝑚𝑎𝑥∆𝜎 = 0,6 ∙ 𝜎

𝑥

∆𝜎

𝑒

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜎

∆𝜎

𝑐

∆𝜎

𝑅

= 0,735 ∙ ∆𝜎 ∙

5 ∙ 10

6

𝑁

1

𝑚

∆𝜎

𝑒

∆𝜎

𝑅

𝛾

𝑓𝑎𝑡

𝜏

𝐼𝐼

=

𝑉𝛽𝛽

𝑉.𝑚𝑎𝑥

∙ 𝑆

𝑥𝑔

𝐼

𝑥

∙ 2𝑎

∆𝜏

𝑐

∆𝜏

𝑅

= ∆𝜏

𝑐

2 ∙ 10

6

𝑁

1
5

𝜏

𝐼𝐼

∆𝜏

𝑅

𝛾

𝑓𝑎𝑡

𝜎 =

(𝛽 ∙ 𝑃

max

)

𝑐

0

∙ 2𝑎

𝑚𝑎𝑥∆𝜎

𝑠

= 0,6 ∙ 𝜎

∆𝜎

𝑒

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜎

𝑠

∆𝜎

𝑐

∆𝜎

𝑅

= 0,735 ∙ ∆𝜎

𝑐

∙

𝑁

𝑁

𝑚

1

𝑚

∆𝜎

𝑒

∆𝜎

𝑅

𝛾

𝑓𝑎𝑡

𝜎 =

(𝛽 ∙ 𝑃

𝑚𝑎𝑥

)

𝑐

0

∙ 2𝑎

𝑚𝑎𝑥∆𝜎

𝑠

= 0,6 ∙ 𝜎

∆𝜎

𝑐

∆𝜎

𝑅

= 0,735 ∙ ∆𝜎

𝑐

∙

𝑁

𝑁

1

𝑚

∆𝜎

𝑒

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜎

𝑠

Strona 15

= 29,760

MPa

<

=

33,252084 MPa

7.3. Środnik pod pasem górnym w miejscu przyspawania żebra.
Zakres zmienności naprężeń od zginania belki

= 47,832

MPa

= 28,699

MPa

= 28,699

MPa

Zakres zmienności naprężeń od nacisku koła

= 62,000

MPa

= 37,200

MPa

= 37,200

MPa

Zakres naprężeń ścinających

= 14,923

MPa

= 14,923

MPa

= 14,923

MPa

Naprężenie główne:

=

48,466187 MPa

Sprawdzenie nośności zmęczeniowej:

= 80,000

MPa

dla karbu w strefie żebra poprzecznego

= 159,608

MPa

Warunek nośności zmęczeniowej:

= 48,466

MPa

<

=

159,60776 MPa

7.4. Środnik nad pasem dolnym w miejscu przyspawania żebra.
Zakres naprężeń na krawędzi środnika

= 59,224

MPa

= 59,224

MPa

= 59,224

MPa

Zakres naprężeń ścinających:

= 13,100

MPa

= 13,100

MPa

= 13,100

MPa

Naprężenia głowne:

=

61,9921 MPa

Sprawdzenie nośności zmęczeniowej:

= 80,000

MPa

dla karbu w strefie żebra poprzecznego

= 159,608

MPa

Warunek nośności zmęczeniowej

= 61,992

MPa

<

=

159,60776 MPa

7.5. Pas dolny w miejscu przyspawania żebra.
Zakres naprężeń:

= 63,047

MPa

= 63,047

MPa

= 63,047

MPa

Warunek nośności zmęczeniowej:

= 63,047

MPa

<

=

159,60776 MPa

7.6. Spoiny pionowe między żebrem podporowym a środnikiem.
Zakres naprężeń:

a

= 4,000

mm

l

= 400,000

mm

∆

𝑅

0 735 ∆

𝑐

𝑁

𝑚

∆𝜎

𝑒

∆𝜎

𝑅

𝛾

𝑓𝑎𝑡

𝜎

𝑥

=

𝑉𝛼𝛼

𝑉.𝑚𝑎𝑥

∙ 𝑒

𝐼

𝑥

𝑚𝑎𝑥∆𝜎

𝑥

= 0,6 ∙ 𝜎

𝑥

∆𝜎

𝑒𝑥

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜎

𝑥

𝜎

𝑧

=

𝛽 ∙ 𝑃

𝑚𝑎𝑥

𝑐

0

∙ 𝑡

𝑤

𝑚𝑎𝑥∆𝜎

𝑧

= 0,6 ∙ 𝜎

𝑧

∆𝜎

𝑒𝑧

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜎

𝑧

𝜏

=

𝑉𝛼𝛼

𝑉.𝑜𝑑𝑝

∙ 𝑆

𝑥𝑔

𝐼

𝑥

∙ 𝑡

𝑤

𝑚𝑎𝑥∆𝜏 = 𝜏

∆𝜏

𝑒

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜏

∆𝜎

𝑒

= 0,5 ∆𝜎

𝑒𝑥

+ ∆𝜎

𝑒𝑧

+ 0,5 (∆𝜎

𝑒𝑥

− ∆𝜎

𝑒𝑧

)

2

+4∆𝜏

𝑒

2

∆𝜎

𝑐

∆𝜎

𝑅

= 0,735 ∙ ∆𝜎 ∙

5 ∙ 10

6

𝑁

1

𝑚

∆𝜎

𝑒

∆𝜎

𝑅

𝛾

𝑓𝑎𝑡

𝜎

𝑥

=

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

∙ (ℎ

𝑤

− 𝑒 )

𝐼

𝑥

𝑚𝑎𝑥∆𝜎

𝑥

= 𝜎

𝑥

∆𝜎

𝑒𝑥

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜎

𝑥

𝜏 =

𝑉𝛼𝛼

𝑉.𝑜𝑑𝑝

∙ 𝑆

𝑥𝑑

𝐼

𝑥

∙ 𝑡

𝑤

𝑚𝑎𝑥∆𝜏 = 𝜏

∆𝜏

𝑒

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆

𝜏

∆𝜎

𝑒

= 0,5 ∙ ∆𝜎

𝑒𝑥

+ 0,5 (∆𝜎

𝑒𝑥

)

2

+4∆𝜏

𝑒

2

∆𝜎

𝑐

∆𝜎

𝑅

= 0,735 ∙ ∆𝜎

𝑐

∙

(5 ∙ 10

6

)

𝑁

𝑚

1
3

∆𝜎

𝑒

∆𝜎

𝑅

𝛾

𝑓𝑎𝑡

𝜎

𝑥

=

𝑀𝛼𝛼

𝑉.𝑚𝑎𝑥

𝑊

𝑥2

𝑚𝑎𝑥∆𝜎

𝑒

= 𝜎

𝑥

∆𝜎

𝑒

= 𝛼

𝑘

∙ 𝑚𝑎𝑥∆𝜎

𝑒

∆𝜎

𝑒

∆𝜎

𝑅

𝛾

𝑓𝑎𝑡

Strona 16

= 89,513

MPa

Wytrzymałość zmęczeniowa

= 80,000

MPa

N =

125000

= 139,288

MPa

= 89,513

MPa

<

=

139,28809 MPa

𝜏 =

𝑉𝛽𝛽

𝑉.𝑚𝑎𝑥

2 ∙ 𝑎 ∙ 𝑙

∆𝜏

𝑐

∆𝜏

𝑅

= ∆𝜏

𝑐

∙

(2 ∙ 10

6

)

𝑁

1
5

𝜏

∆𝜏

𝑅

𝛾

𝑓𝑎𝑡

Strona 17

Strona 18

Strona 19

Strona 20

Strona 21

Strona 22

Strona 23

Strona 24